Statistics and Application
Vol.07 No.01(2018), Article ID:23700,7
pages
10.12677/SA.2018.71004
Analysis about Influence of College Students’ Time Management on Academic Based on Structural Equation Modeling
Wenwen Li, Jiawei Fan, Yuchao He, Jianyong Xue, Yahui Dong, Sanzhi Shi*
College of Science, Changchun University of Science and Technology, Changchun Jilin
Received: Jan. 17th, 2018; accepted: Jan. 31st, 2018; published: Feb. 7th, 2018

ABSTRACT
The structural equation model is a mathematical analysis method to establish and statistically predict the causality of multivariate variables. From the perspective of psychology, this article sets the academic as the four dimensions of learning ability, creative thinking, verbal expression ability and communication and cooperation ability, setting time as the three dimensions of time value, time monitoring and time efficacy. 700 questionnaires were distributed to students in four colleges and universities in Changchun, and the questionnaire reliability was analyzed by using SPSS statistical software. The reliability of the questionnaire was 0.893, indicating good reliability. Using the AMOS software to establish the model coefficient estimation statistic and the structural equation model path map, the P values of all the path coefficients are all below the significance level of 0.05, indicating that there is a significant positive correlation between the time management and the academic level of undergraduates and the related structural equations are established. The results show that good time management can not only improve students' learning performance, but also lay a good foundation for further socialization of personality.
Keywords:Structural Equation Model, Correlation Analysis, Time Management, College Students, Academic
基于结构方程模型的大学生时间管理 对学业影响的相关性分析
李文文,范佳玮,贺煜超,薛建勇,董亚辉,施三支*
长春理工大学理学院,吉林 长春

收稿日期:2018年1月17日;录用日期:2018年1月31日;发布日期:2018年2月7日

摘 要
结构方程模型是一种分析建立、统计预测多变量因果关系的数学分析方法。本文从心理学的角度出发,将学业设为学习能力、创造性思维、语言表达能力、交流合作能力四个维度,将时间设为时间价值感、时间监控观和时间效能感三个维度。对长春市四所高校的学生发放700份调查问卷,使用SPSS统计软件进行问卷信度分析,得到问卷信度为0.893,表明信度良好。用AMOS软件建立模型系数估计统计量以及结构方程模型路径图,得到所有项路径系数的P值都在0.05的显著性水平以下,表明大学生时间管理和学业水平存在显著正相关,并据此建立了相关的结构方程。研究结果显示,好的时间管理不仅可以提高学生的学习绩效,还可以为促进人格的进一步社会化奠定良好的基础。
关键词 :结构方程模型,相关性分析,时间管理,大学生,学业

Copyright © 2018 by authors and Hans Publishers Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/


1. 引言
现阶段,许多专家及学者试图从大学生的时间管理角度去研究影响大学生学业水平的因素。黄希庭等人(2001) [1] 提出时间管理倾向是一种个体在运用时间方式上所表现出来的心理和行为方面的人格特征,具有多维度、多层次的心理结构,主要由时间价值感、时间监控观和时间效能感构成。魏佳(2015) [2] 的研究表明在时间管理倾向的三个维度中,时间效能感主要影响学业成绩,与大学生学业成绩成显著正相关。而李茹锦(2008) [3] 在不同的成就对学业成绩的间接作用的研究中发现,学业成绩与时间监控感、时间效能感成显著正相关,但时间效能感不在多元线性回归中显现。以上的研究都是借用传统的统计方法实现的,但对于这种传统的统计方法,其中因素自身的测量和因素之间的关系是分开出的,先是对因素进行测量,评估概念的信度和效度,接着通过评估标准,将测量资料用于进一步的分析。为了区别于传统方法,本文基于结构方程模型对大学生时间管理对学业的影响进行相关性研究。
结构方程模型 [4] 便于我们从诸多的子维度中找出关联度最大的影响因子,Heidi Janssens等人(2016) [5] 利用结构方程模型对工作压力、长期病假和受欺凌三者潜在的关系进行了研究,Florence Fulk、Paul Succop等人(2016) [6] 通过结构方程模型,在已有统计数据的基础上,找出了被调查个体所在地空气、土壤、灰尘中锰含量及个体取暖方式、父母受教育水平、室外活动时间对个体摄入锰含量的相关关系等。
本文构建结构方程模型,通过将难以直接衡量的学习能力,创造性思维,语言表达能力和交流合作能力以调研打分为测量变量予以概念化,进向通过测量变量之间的协方差关系研究潜变量之间的关系,拟合结果可以清晰地显示出学业水平和时间管理能力的预测关系,其主要包括测量方程和结构方程两类。
2. 结构方程模型原理和模型建构
结构方程模型(Structure Equation Modeling)是一种分析建立、统计预测多变量因果关系的数学分析方法,涵盖了回归分析、因子分析、通径分析、协方差分析等诸多一元及多元统计分析方法所具备的优点 [7] 。综合了传统统计方法中因子分析和路径分析的各项优点,通过为难以直接测量的潜变量设定观测变量,借助这些可以用于统计分析的观测变量之间的关系进一步研究潜在变量之间的关系。结构方程模型不但可以使研究人员在分析中处理测量误差,而且又可以分析潜变量之间的结构关系。因此可以将结构方程模型的联立方程组分成以下两类:
1) 测量方程
测量方程是表示观测变量 与潜变量 之间关系的 方程组。其中 是表示外生指标组成的向量, 是表示内生指标组成的向量, 用来表示外生指标与外生潜变量之间的关系和内生指标与内生潜变量之间的关系, 是外生指标 的误差项及内生指标 的误差项, 是内生潜变量, 是外生潜变量。
2) 结构方程
结构方程组主要用于表示潜变量与潜变量之间的关系。其中 表示内生潜变量之间的关系, 是外生潜变量对内生潜变量的影响, 是外生潜变量, 是结构方程的残差项。
由这两组方程,再加上一些模型的设定,通过一种迭代求解过程,就能计算出结构方程模型中的各个参数。
3. 时间管理与学业相关性的建模
3.1. 变量选取
本文中的时间价值感,时间监控感和时间效能感三个外生潜变量分别用 表示;学习能力,创造性思维,语言表达能力和交流合作能力四个内生潜变量分别用 表示。
是由内生指标组成的向量,分量对应文中的 ; 是由外生指标组成的向量,分量分别对应本文中的 。
表示外生指标X的误差项和内生指标Y的误差项。在本文中内生指标 的误差项为 外生指标 的误差项为 ; 表示结构方程的残差项,本文中 为学习能力的残差项, 为创造性思维的残差项, 为语言表达能力的残差项, 为交流合作能力的残差项; 为外生指标与外生潜变量之间的关系以及内生指标与内生潜变量之间的关系, 对学习能力的关系记为 , 和创造性思维的关系记为 ; 和语言表达能力的关系记为 ; 和交流合作能力之间的关系记为 ; 和时间价值感之间的关系记为 ; 和时间监控感之间的关系记为 ; 对时间效能感之间的关系记为 。
是外生潜变量对内生潜变量的影响,在本文中时间价值感对学习能力,创造性思维,语言表达能力,交流合作能力的关系记为 ,时间控制感学习能力,创造性思维,语言表达能力,交流合作能力的关系记为 ,时间效能感对学习能力,创造性思维,语言表达能力,交流合作能力的关系记为 。
3.2. AMOS分析
本对全日制本科在校大学生,选取吉林大学、东北师范大学、长春理工大学和长春大学四所高校的学生展开调查研究(分别作为“985高校”“211高校”“普通一本高校”和“普通二本高校”的代表)。通过编辑调查问卷。通过问卷星网络平台和实地发放调查问卷。共计发放调查问卷700份,最终回收有效问卷685份。
设时间管理和学业水平两大项。其中时间管理项下设“时间价值感”、“时间监控观”、“时间效能感”三个维度,包含的项目数分别为2、4、3,共9个题项。学业水平项下设“学习能力”“创造性思维”“语言表达能力”“交流合作能力”四个维度,包含的项目数分别为3、3、2、3,共11个题项。采用“1 = 完全不符合”到“5 = 完全符合”计分,得分高者则表明被试者对于时间的功能和价值具有较高的评价,或者在日常学习中能够较多地使用这些时间监控行为。
本文使用AMOS软件 [8] 对参数进行拟合,选择最大似然估计方法。在AMOS软件中,利用Analyze菜单下的Calculate Estimate进行模型拟合,输出路径系数的统计检验结果,如表1所示,这是非标准化回归的检验结果。
可以看出,所有项的路径系数的P值都在0.05的显著性水平以下,Estimate路径系数值表示预测变量变化一单位,相应的因变量会变化路径系数大小的单位,如时间监控感增加一单位会使得学习能力增加一单位。
依据模型系数估计统计量构建出相关的结构方程模型路径图(图1)。
Table 1. Model coefficient estimation statistics
表1. 模型系数估计统计量
***在0.05水平(双侧)上显著相关。
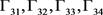
Figure 1. Structural equation model path map
图1. 结构方程模型路径图
3.3. 建立结构方程模型
以图1的结构方程模型为依据,我们可以建立如下的结构方程表达式:
由于其所表示关系的项之间的相关性较小,以及用SEM模型验证路径系数的P值不在0.05显著性水平下,把值设为0,则可得:
4. 模型结果分析
4.1. 问卷可信度分析
由于信度分析能够分析出评价调查的稳定性和可靠性。所以我们将收集的数据经过量化处理后导入SPSS软件进行信度分析。分析结果如表2所示。
一般情况下,信度分析达到0.8左右时则可以表示问卷的信度良好,0.9以上则表示信度极好。从表2可以看出问卷信度为0.893,信度良好。
4.2. 学生时间管理和学习能力的相关性总体分析
从表3可以看成。时间管理与学业水平有很强的相关性且影响显著。从研究中发现,学习成绩较为出色的学生,其时间管理倾向的特质比学习成绩相对逊色的学生更为突出。时间管理不仅提高学生的学习绩效,更重要的是可以促进人格的进一步的社会化创造良好的基础。
4.3. 从不同的维度分析
为了更好的研究大学生时间管理与其学业之间的影响,我们根据调查问卷的结果又从不同性别、年级,高校,家乡所在地四个方面进行了详细的分析,得到了以下结论:
1) 心理学研究表明,女性多属于场依存型,男性则多属于场独立型。步入大学,学生可以自由支配的时间增多,师长的约束减少,男生的独立适应能力明显高于女生,导致男生的时间管理倾向总体要强于女生。但女生因为从小被灌以做事认真、踏实、稳重的思想,所以在时间监控感上要优于男生,更容易在规定时间内完成学习任务。学习能力、交流合作能力要优于男生。同时有研究指出,男生和女生的大脑发育从小就是不一样的,这就导致女生的抽象思维和逻辑思维不如男生,所以男生的创造性思维要优于女生,当然语言表达能力也要优于女生。
2) 从不同地区的角度来说,南方大都是经济发达省份,人口较多,竞争也就相对比较激烈,这就使得南方的教学质量高于北方的教学质量,学生的学习观念比较强,使得其拥有较强的学习能力。相比之下,北方学生没有了地域优势,只能靠自身的努力来发展,所以北方学生对自身的要求严格,在时间管理上要优于南方学生。
3) 对于不同高校的学生,985和211高校的学生学习能力及时间管理能力相比一本学生和二本学生
Table 2. Reliability statistics
表2. 可靠性统计量
Table 3. Student time management and learning ability of the overall analysis of the correlation table
表3. 学生时间管理和学习能力的相关性总体分析表
要较好一些。主要有两方面原因,一方面是985和211高校的校园学习氛围相比之下较好,学习资源也相对较多,一个良好的学习环境对学生的学业发展也是很重要的。另一方面985和211高校的学生大部分都是从小就是对学习能力和时间管理能力要求较严格的,在成长的过程中已经形成了良好的习惯,再加上来自名校上的自信,让他们更容易取得好成绩。
4) 从心理学角度来说,初到一个陌生的环境,人本能的想要证明自己,这在211,985名校中尤为明显。但与此同时,大一的学生并没有完全掌握高中与大学学习方法上的不同,导致学习效果并不明显,相比之下,大二、大三的学生学习能力较强,同时,随着学科竞赛的加入,高年级学生的交流合作及语言表达能力也得到了加强。
5. 结论
本文调研了大学生时间管理与其学业之间的影响,并建立了结构方程模型进行分析,研究结果表明,大学生时间管理和学业水平存在显著正相关。为了使大学生能够更好的管理时间来提升学业水平,本文给出以下建议:要有时间管理意识并努力培养自己的时间管理意识;要有明确的目标并为此目标的实现制定详细的计划做到高效的时间管理;学会并保持做事有条理并学会使用任务清单;分清主次并牢记要事为先;劳逸结合,张弛有度,才能更有效率的学习;牢牢把握效率与效果的关系。
基金项目
吉林省自然科学基金(20140101199JC);大学生创业创新课题(40103-129645)。
文章引用
李文文,范佳玮,贺煜超,薛建勇,董亚辉,施三支. 基于结构方程模型的大学生时间管理对学业影响的相关性分析
Analysis about Influence of College Students’ Time Management on Academic Based on Structural Equation Modeling[J]. 统计学与应用, 2018, 07(01): 25-31. http://dx.doi.org/10.12677/SA.2018.71004
参考文献 (References)
- 1. 黄希庭, 张志杰. 青少年时间管理倾向量表的编制[J]. 心理学报, 2001, 33(4): 338-343.
- 2. 魏佳. 大学生时间管理倾向与学业成绩的相关分析[J]. 高等教育, 2015(35): 34-40.
- 3. 李茹锦. 不同成就目标定向大学生的时间管理倾向及其与学业成绩的关系[D]: [硕士学位论文]. 济南: 山东师范大学, 2008: 168-194.
- 4. 侯杰泰, 温忠麟, 成子娟. 结构方程模型及其应用[M]. 北京: 教育科学出版社, 2014.
- 5. Janssens, H., Braeckman, L., De Clercq, B., Casini, A., De Bacquer, D., Kittel, F. and Clays. E. (2016) The Indirect Association of Job Strain with Long-Term Sickness Absence Through Bullying: A Mediation Analysis Using Structural Equation Modeling. BMC Public Health, 6, 851-863. https://doi.org/10.1186/s12889-016-3522-y
- 6. Fulk, F., Succop, P., Hilbert, T.J., Beidler, C., Brown, D., Reponen, T. and Haynes, E.N. (2016) Pathways of Inhalation Exposure to Manganese in Children Living near a Ferromanganese Refinery: A Structural Equation Modeling Approach. Science of the Total Environment, 21, 332-340.
- 7. Lee, S. and Ahn, H. (2009) Structural Equation Model for EDI Controls: Controls Design Per-spective. Expert Systems with Applications, 36, 1731-1749. https://doi.org/10.1016/j.eswa.2007.12.008
- 8. 郭志刚. 社会统计分析方法——SPSS软件应用[M]. 北京: 中国人民大学出版社, 1999.
