Advances in Applied Mathematics
Vol.04 No.04(2015), Article ID:16356,10
pages
10.12677/AAM.2015.44041
Numerical Inversion for the Fractional Order in the Variable-Order Time-Fractional Diffusion Equation
Di Liu, Chunlong Sun, Gongsheng Li*, Xianzheng Jia
*通讯作者。
School of Sciences, Shandong University of Technology, Zibo Shandong
Received: Oct. 22nd, 2015; accepted: Nov. 7th, 2015; published: Nov. 12th, 2015
Copyright © 2015 by authors and Hans Publishers Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/



ABSTRACT
An implicit finite difference scheme is introduced to solve the variable-order time-fractional diffusion equation, and an inverse problem of determining the variable fractional order is set forth using the additional measurements at one interior point. The homotopy regularization algorithm is applied to solve the inverse problem, and numerical examples are presented. The computational and inversion results demonstrate that the variable order has important influence on the problem, and that the computations become effective when the variable order goes to 1.
Keywords:Variable-Order Fractional Diffusion Equation, Inverse Problem, Homotopy Regularization Algorithm, Numerical Inversion

变分数阶扩散方程微分阶数的数值反演
刘迪,孙春龙,李功胜*,贾现正
山东理工大学理学院,山东 淄博
收稿日期:2015年10月22日;录用日期:2015年11月7日;发布日期:2015年11月12日

摘 要
对于变分数阶扩散方程,给出一个隐式差分求解格式。进一步讨论由内点观测数据确定微分阶数的一个反问题,应用同伦正则化算法在不同参数取值条件下进行数值反演模拟。数值结果表明当微分阶数接近于1时,数值求解及其参数反演效果较好。
关键词 :变分数阶扩散方程,反问题,同伦正则化,数值反演

1. 引言
近二十年来,分数阶微积分、分数阶偏微分方程及其应用研究广受关注[1] -[5] 。对于经典的一维非稳态扩散方程,其时间导数、空间导数分别为1阶和2阶的整数阶导数。当时间导数的阶数由1变为(0, 1)区间的一个数,或者空间导数的阶数由2变为(1, 2)区间的一个数时,就得到分数阶反常扩散方程。分数阶扩散方程在物理学、力学、环境科学、水文地质学及金融学等领域得到了广泛的应用。进一步,若分数阶导数的阶数不是(0, 1)或(1, 2)区间上的一个数,而是一个随着空间/时间变量而变化的函数,则可得到变阶的分数阶导数 [6] [7] ,进而可得到所谓的变分数阶扩散方程.变分数阶模型及相应的变阶算子为描述复杂动力系统问题提供了新的数学构架,已成为分数阶扩散研究的一个新领域。
从已有文献看,Coimbra [8] ,Copper与Crown [9] ,以及Tseng [10] 等分别从粘弹性力学、地理数据与信号处理研究等领域展示了变阶微分算子的应用。数学上,鉴于适定性理论研究的困难性,目前对于变分数阶扩散方程的研究主要集中在数值求解方面,且主要是有限差分法。刘发旺教授及其团队对于变分数阶扩散模型的差分求解方法做出了一些开创性的工作 [11] - [14] 。国内也有一些类似的研究工作,如马维元等 [15] ,马亮亮等 [16] 对不同类型的变阶扩散方程给出了有效的隐式差分格式。
另一方面,一旦建立了一个分数阶扩散模型及其正问题求解方法,确定模型中难以测量的关键参数就成为一类很重要的科学问题。比如,反映空间或时间相关性的微分阶数的确定问题,反映空间非均质性的扩散系数的确定问题,反映外界力作用属性的源/汇项的确定问题,等等,这就导致了对于分数阶反常扩散中的参数反演问题研究。关于分数阶扩散相关反问题的研究,业已经成为数学物理反问题研究的一个热点 [17] - [24] 。不过,国内外对于变分数阶相关反问题的研究还未见有文献报道。虽然对于变分数阶扩散方程正/反问题的理论分析研究难以展开,但借助于正问题的数值解和适当的反演算法,开展变阶扩散模型参数的数值反演研究对于理解和把握变分数阶扩散行为过程具有重要的参考价值。
微分阶数是刻化分数阶扩散的首要指标,也是分数阶扩散区别于整数阶扩散的重要参数。由于实际问题中微分阶数是未知的,更是难以通过实验手段直接测量获得,因而有必要开展确定和识别微分阶数的反问题研究。对于变分数阶扩散方程,由于微分阶数表现为时间/空间变量的一个函数,对其进行数值反演更具有一定的难度。
本文将探讨常系数变分数阶扩散方程中确定时间依赖微分阶数的数值反演问题。文中首先利用对变分数阶导数的差分离散,得到求解正问题的一个隐式差分格式,证明差分格式的收敛性与稳定性,并给出一个数值算例。进一步,应用同伦正则化算法对方程中时间依赖的微分阶数进行数值反演,给出数值反演算例,并讨论时间/空间步长及数据扰动水平等因素对反演算法的影响。
2. 正问题及其数值求解
考虑变分数阶扩散方程
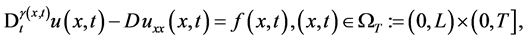 (1)
(1)
初值条件为
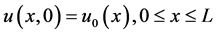 , (2)
, (2)
边值条件为
 , (3)
, (3)
其中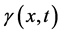 为关于空间变量
为关于空间变量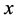 与时间变量
与时间变量 的微分阶数,满足条件
的微分阶数,满足条件 ,
, 为扩散系数,
为扩散系数, 为源/汇项,
为源/汇项,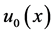 是初始函数。在状态量
是初始函数。在状态量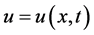 关于时间变量
关于时间变量 充分光滑的条件下,变阶导数
充分光滑的条件下,变阶导数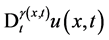 可由Caputo意义下的分数阶导数定义为:
可由Caputo意义下的分数阶导数定义为:
 , (4)
, (4)
其中 为通常的Gamma函数。
为通常的Gamma函数。
注意到变分数阶导数的阶数是随 变化的,其相应正问题的求解相比一般分数阶扩散模型的求解困难不少。下面基于对变分数阶导数(4)的数值积分离散,建立求解正问题(1)~(3)的一个隐式差分格式。
变化的,其相应正问题的求解相比一般分数阶扩散模型的求解困难不少。下面基于对变分数阶导数(4)的数值积分离散,建立求解正问题(1)~(3)的一个隐式差分格式。
2.1. 差分格式
设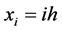 ,
, ,其中
,其中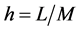 和
和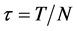 分别是空间和时间步长。记
分别是空间和时间步长。记 ,在
,在 处,变分数阶导数离散为:
处,变分数阶导数离散为:
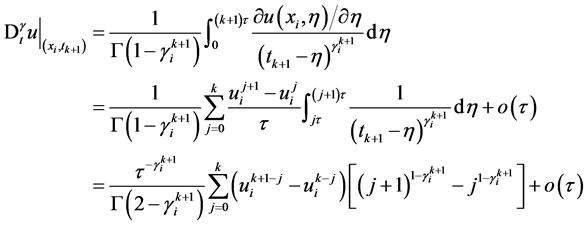 (5)
(5)
对方程(1)中的二阶整数阶导数用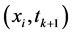 处中心差商近似,可得
处中心差商近似,可得
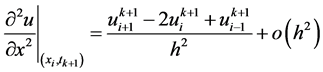 . (6)
. (6)
记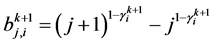 ,
,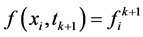 ,将(5),(6)带入方程(1),并略去高阶项得到
,将(5),(6)带入方程(1),并略去高阶项得到
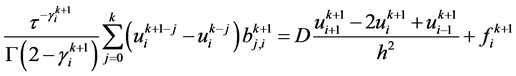 . (7)
. (7)
上式两边同乘以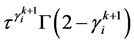 ,并记
,并记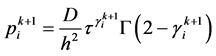 ,即有
,即有
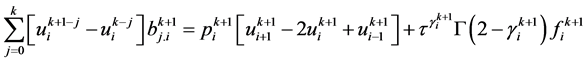 . (8)
. (8)
注意到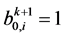 ,上式整理即得
,上式整理即得
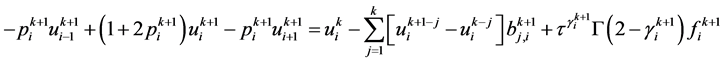 . (9)
. (9)
进一步记为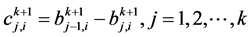 ;利用零边值条件
;利用零边值条件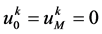 ,记
,记
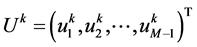 ,
, ,
,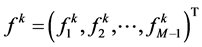 ,可得以矩阵形式表示的差分格式
,可得以矩阵形式表示的差分格式
 (10)
(10)
其中系数矩阵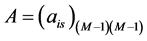 定义为
定义为
 , (11)
, (11)
且系数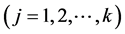
 ,
,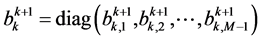 ,以及
,以及
 ,这里
,这里 表示取对角阵。
表示取对角阵。
由于对于任意的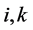 成立
成立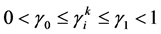 ,即知
,即知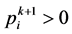 ,从而可知由(11)式定义的矩阵
,从而可知由(11)式定义的矩阵 是严格对角占优的三对角阵,即知
是严格对角占优的三对角阵,即知 可逆且差分方程(10)有唯一解。进一步,利用与文 [23] [25] 完全类似的方法,可以证明差分方程(10)是无条件稳定和收敛的。
可逆且差分方程(10)有唯一解。进一步,利用与文 [23] [25] 完全类似的方法,可以证明差分方程(10)是无条件稳定和收敛的。
定理1 由(10)式给出的隐式差分格式是无条件稳定的,且对于任意有限时间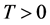 是收敛的。
是收敛的。
证明 根据Gerschgorin圆盘定理,可知
 ,
,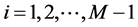 .
.
其中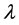 为矩阵
为矩阵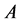 的任一特征值。由上式可得
的任一特征值。由上式可得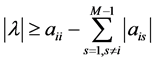 ,
, 。注意到(11)式,即有
。注意到(11)式,即有 ,可知
,可知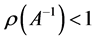 。根据矩阵范数的性质,可知存在
。根据矩阵范数的性质,可知存在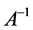 的某种范数
的某种范数 ,使得成立
,使得成立 。为书写方便,以下稳定性、收敛性估计中的范数仍用
。为书写方便,以下稳定性、收敛性估计中的范数仍用 表示。
表示。
记初始扰动为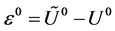 ,第
,第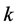 层的扰动为
层的扰动为 。由(10)式的线性性,可得
。由(10)式的线性性,可得
 . (12)
. (12)
因而基于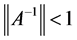 ,即有
,即有 。根据归纳法,若假设对任意
。根据归纳法,若假设对任意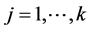 ,成立
,成立 ,则有
,则有
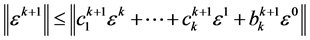 . (13)
. (13)
注意到对每一个 (
(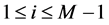 ),成立基本等式
),成立基本等式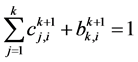 ,由(13)式即得
,由(13)式即得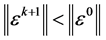 ,即差分格式(10)是无条件稳定的。
,即差分格式(10)是无条件稳定的。
进一步,记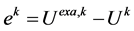 (
(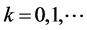 ),其中
),其中 表示解在第
表示解在第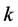 层的精确值。由
层的精确值。由 及差分格式线性性,得到:
及差分格式线性性,得到:
 , (14)
, (14)
其中 表示第
表示第 层的截断误差。由(5),(6)可知,存在常数
层的截断误差。由(5),(6)可知,存在常数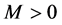 ,成立
,成立
 ,
,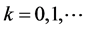 . (15)
. (15)
基于(14)~(15)式,类似于稳定性的估计方法可得误差估计
 , (16)
, (16)
其中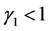 为微分阶数
为微分阶数 的一个上界。定理1证毕。
的一个上界。定理1证毕。
2.2. 数值算例
取微分阶数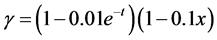 ,初始函数
,初始函数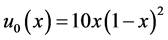 ,扩散系数
,扩散系数 ,且
,且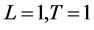 ,源项为
,源项为
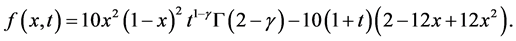
易知正问题(1)~(3)的精确解为
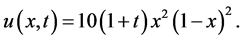
不妨取相同的空间与时间步长,应用差分格式(10)进行计算,结果列于表1,其中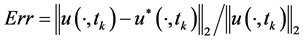 表示
表示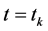 时的解误差,
时的解误差, 表示真解,
表示真解, 表示差分解。
表示差分解。
由表1可以看出,随空间/时间步长的变小,解误差迅速变小;但当 时,解误差有增大的趋势,其原因之一是步长变小时的计算误差积累,之二是计算中选取了相同的空间、时间步长。有关计算格式的改进,我们将另文再述。取
时,解误差有增大的趋势,其原因之一是步长变小时的计算误差积累,之二是计算中选取了相同的空间、时间步长。有关计算格式的改进,我们将另文再述。取 ,图1绘制了
,图1绘制了 时的数值解与真解。
时的数值解与真解。
3. 反问题及反演算法
一般来说,正问题指偏微分方程的定解问题,反问题指数学物理中的反问题。反问题是20世纪五、六十年代兴起的属于偏微分方程理论与工业应用及计算数学研究领域的交叉学科方向。对于一个定解问题,如果模型算子或边界算子的某些系数未知,或初始状态未知,或右端源项未知,又或解的存在区域特征未知,等等,则在物理规律的限制下,额外给出关于解的某些附加信息,进而确定出解与未知项(参数),这就是所谓的反问题。
设方程(1)中的微分阶数 具有变量分离的形式,即设
具有变量分离的形式,即设 ,其中
,其中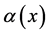 是已知的,而
是已知的,而 是未知的。给定区域某个内点
是未知的。给定区域某个内点 处的若干次观测值作为附加数据,即有在有限个时间点处测量得到的有限维数据,记为
处的若干次观测值作为附加数据,即有在有限个时间点处测量得到的有限维数据,记为
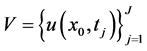 , (17)
, (17)
Table 1. The solutions errors with space/time steps at
表1. 空间/时间步长与解误差(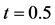 )
)
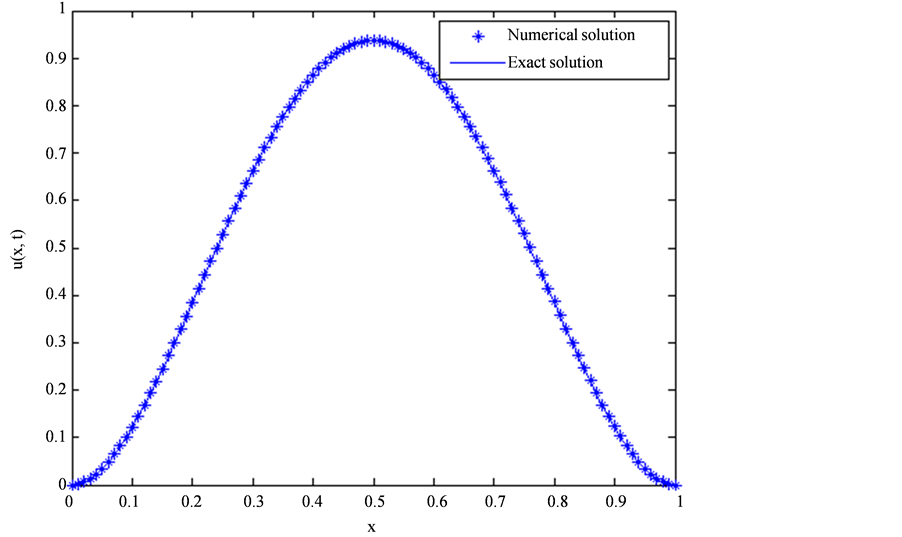
Figure 1. The exact and numerical solutions at
 for
for
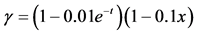
图1.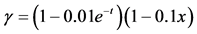 ,
, 时的数值解与真解
时的数值解与真解
其中 是观测点,
是观测点,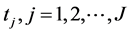 为观测时刻,则由(1)~(3)联合附加数据条件(17)形成一个确定
为观测时刻,则由(1)~(3)联合附加数据条件(17)形成一个确定
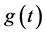 的参数反演问题。本文仅考虑该反问题的数值反演。以下给出确定
的参数反演问题。本文仅考虑该反问题的数值反演。以下给出确定 的同伦正则化算法(见[23] [26] 等)。
的同伦正则化算法(见[23] [26] 等)。
设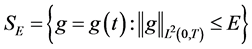 为
为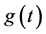 的一个容许集,且设
的一个容许集,且设 为
为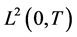 的一组基。实际计算中取
的一组基。实际计算中取 的有限维近似,即设
的有限维近似,即设
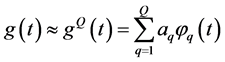 , (18)
, (18)
其中 (
( )为展开系数。记
)为展开系数。记 ,则寻求
,则寻求 等同于求解向量
等同于求解向量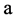 。这样,对于任意给定的
。这样,对于任意给定的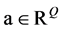 ,利用差分格式(10)求解正问题所得其解记为
,利用差分格式(10)求解正问题所得其解记为 ,并在
,并在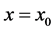 处和
处和 时刻赋值,即得所谓的计算输出数据(向量),记之为
时刻赋值,即得所谓的计算输出数据(向量),记之为
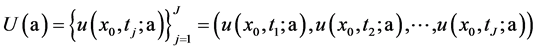 . (19)
. (19)
基于最优化的思想,反演问题的求解又可化为一个极小问题的求解:
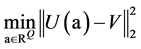 . (20)
. (20)
一般来说,上述极小问题的求解是病态的。利用同伦正则化方法,极小问题(20)的求解可转化为:
 , (21)
, (21)
其中 为同伦参数。首先对于给定的
为同伦参数。首先对于给定的 ,设
,设
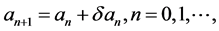 (22)
(22)
其中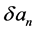 称为摄动量,
称为摄动量,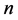 为迭代次数。其次,利用线性化近似:
为迭代次数。其次,利用线性化近似:
 ,
,
基于(21)式,定义关于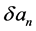 的误差函数:
的误差函数:
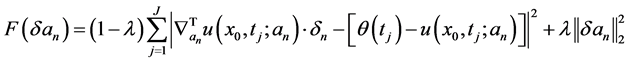 .(23)
.(23)
再利用数值微分近似,记
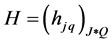 ,
,
 , (24)
, (24)
其中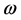 为数值微分步长,
为数值微分步长, (
( )为
)为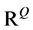 空间的标准基。再次利用矩阵(向量)的表示,极小问题
空间的标准基。再次利用矩阵(向量)的表示,极小问题 的求解等价于求解规范方程:
的求解等价于求解规范方程:
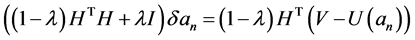 , (25)
, (25)
则对于给定的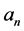 ,通过选择适当的同伦参数
,通过选择适当的同伦参数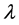 ,由(25)式计算可得一个最佳摄动量为:
,由(25)式计算可得一个最佳摄动量为:
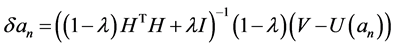 . (26)
. (26)
算法实施中,对于给定的精度 ,在每一步判断是否成立
,在每一步判断是否成立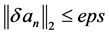 ;若成立,则
;若成立,则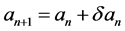 即为所求;否则,用
即为所求;否则,用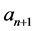 替代
替代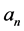 继续求解,直至满足精度要求或迭代步数要求。
继续求解,直至满足精度要求或迭代步数要求。
4. 数值反演
本节给出数值反演算例,算例中的模型参数同于第2.2节相应正问题数值算例中的取值,微分阶数真值仍取为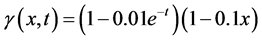 ,我们的问题是利用
,我们的问题是利用 处的观测数据和同伦算法反演确定依赖于时间的函数
处的观测数据和同伦算法反演确定依赖于时间的函数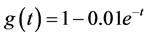 。注意到拟神经网络方法中Sigmoid型传输函数取值于(0, 1)且非负、单调下降的性质,选取同伦参数为
。注意到拟神经网络方法中Sigmoid型传输函数取值于(0, 1)且非负、单调下降的性质,选取同伦参数为
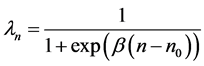 , (27)
, (27)
其中 是迭代次数,
是迭代次数,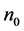 是当同伦参数取值下降至0.5时的预估迭代次数,而
是当同伦参数取值下降至0.5时的预估迭代次数,而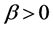 是校正参数。本文实际计算中取
是校正参数。本文实际计算中取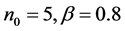 。此外,取数值微分步长
。此外,取数值微分步长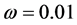 ,控制迭代精度
,控制迭代精度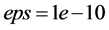 ,且取多项式空间
,且取多项式空间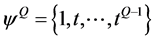 作为逼近空间。根据
作为逼近空间。根据 的展开式,真解
的展开式,真解 在
在 中近似表示为向量
中近似表示为向量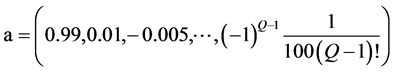 。
。
1) 先取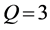 ,即
,即 ,考察初始迭代对反演算法的影响。计算结果列于表2,其中
,考察初始迭代对反演算法的影响。计算结果列于表2,其中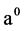 表示初始迭代值,
表示初始迭代值,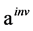 表示反演解,
表示反演解, 表示反演解与真解的误差,
表示反演解与真解的误差,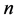 为迭代次数。
为迭代次数。
由表2可以看出,初始值选取对算法影响较大,且当其离真解较远时,迭代步数也相对较多。下面考察逼近空间的维数变化对反演算法的影响。
2) 当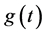 在不同维数的逼近空间展开时,其有不同的表示形式。由于截断误差的存在,理论上逼近空间维数越高,则反演结果应该越精确。分别在维数为
在不同维数的逼近空间展开时,其有不同的表示形式。由于截断误差的存在,理论上逼近空间维数越高,则反演结果应该越精确。分别在维数为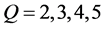 的逼近空间中反演,初始迭代相应取为
的逼近空间中反演,初始迭代相应取为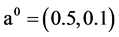 ,
,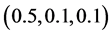 ,
, 及
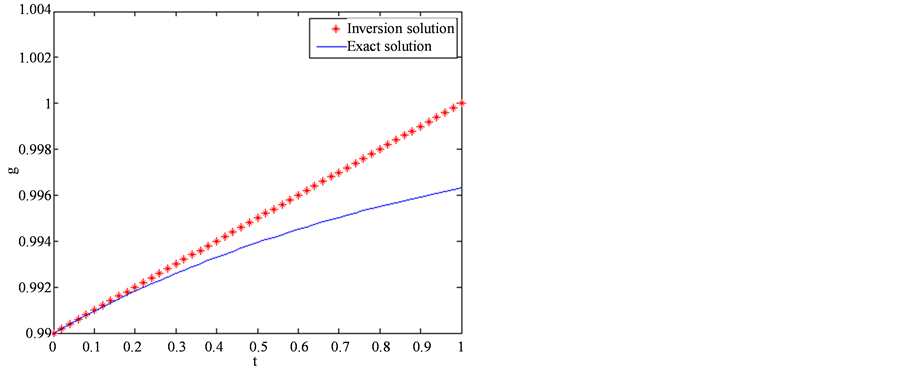
及 ,反演解与真解的图像分别绘于图2的(a),(b),(c)及(d)。
,反演解与真解的图像分别绘于图2的(a),(b),(c)及(d)。
由图2可以看出,随着逼近空间维数的增大,反演解越来越逼近于真解,这反映了算法有限维逼近
的收敛性。事实上,根据(18)式,对于正交基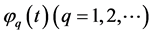 成立
成立 ,即理论上表明逼近
,即理论上表明逼近
空间的维数越高,数值反演解越接近真值。
3) 实际问题中,附加数据往往带有某种误差,对于扰动数据实施反演算法是反问题数值方法研究的重要内容。设带扰动的附加数据表示为
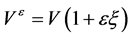 , (28)
, (28)
其中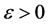 是扰动水平,
是扰动水平,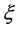 为取值于[−1,1]的随机数。注意到扰动的随机性,每次反演计算的结果并不一样。仍取
为取值于[−1,1]的随机数。注意到扰动的随机性,每次反演计算的结果并不一样。仍取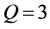 ,分别在扰动水平
,分别在扰动水平 及
及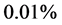 下反演,表3列出了连续十次反演的平均结果,其中
下反演,表3列出了连续十次反演的平均结果,其中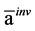 表示反演解的平均值,
表示反演解的平均值,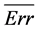 表示真解与反演解平均值的相对误差,
表示真解与反演解平均值的相对误差, 表示平均迭代次数。
表示平均迭代次数。
从表3可以看出,随着数据扰动水平的减小,反演解与精确解误差逐渐变小,表明了反演算法的数值稳定性。
5. 结束语
本文给出了一类变分数阶反常扩散方程正问题求解的差分格式,并证明了格式的无条件稳定性和收敛性。进一步,讨论了关于时间依赖微分阶数的反问题,应用同伦正则化算法给出了精确数据与扰动数据情形下得数值反演,并讨论了初始迭代与数据扰动对反演结果的影响。文中结果表明,无论是正问题的求解,还是关于微分阶数的数值反演,可变微分阶数的取值都应在1的附近,这反映出变分数阶扩散问题求解的病态性较高。对于变阶反常扩散问题,构建更有效的正问题求解格式以及参数反演算法是今后的一项主要工作。
Table 2. The inversion results with initial iterations
表2. 初始迭代选取对反演结果的影响
Table 3. The inversion results with noisy data
表3. 数据扰动对反演结果的影响
 (a) (b)
(a) (b)
 (c) (d)
(c) (d)
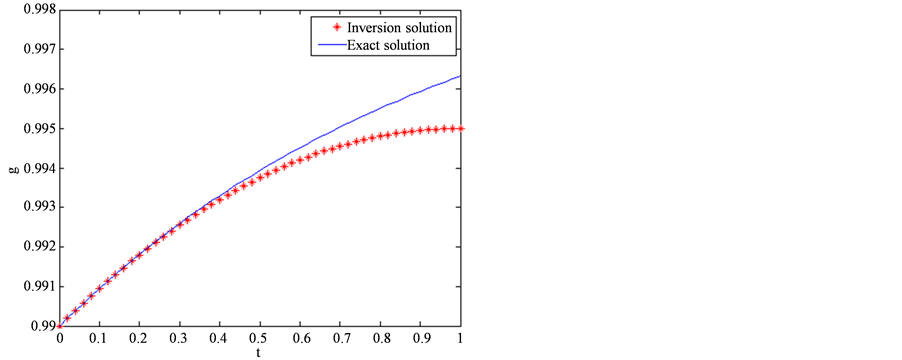
Figure 2. The exact and inversion solutions for the fractional order in different approximate spaces. (a) Q = 2; (b) Q = 3; (c) Q = 4; (d) Q = 5
图2. 不同逼近空间中微分阶数的反演解与真解。(a) Q = 2;(b) Q = 3;(c) Q = 4;(d) Q = 5
基金项目
国家自然科学基金资助项目(Nos. 11371231, 11071148)。
文章引用
刘迪,孙春龙,李功胜,贾现正. 变分数阶扩散方程微分阶数的数值反演
Numerical Inversion for the Fractional Order in the Variable-Order Time-Fractional Diffusion Equation[J]. 应用数学进展, 2015, 04(04): 326-335. http://dx.doi.org/10.12677/AAM.2015.44041
参考文献 (References)
- 1. Miller, K.S. and Ross B. (1993) An Introduction to the Fractional Calculus and Fractional Differential Equations. John Wiley, New York.
- 2. Podlubny, I. (1999) Fractional Differential Equations. Academic, San Diego.
- 3. Kilbas, A.A., Srivastava, H.M. and Trujillo, J.J. (2006) Theory and Applications of Fractional Differential Equations. Elsevier, Amsterdam.
- 4. 陈文, 孙洪广, 李西成. 力学与工程问题的分数阶导数建模[M]. 北京: 科学出版社, 2010.
- 5. 郭柏灵, 蒲学科, 黄凤辉. 分数阶偏微分方程及其数值解[M]. 北京: 科学出版社, 2011.
- 6. Samko, S.G. and Ross B. (1993) Integration and Differentiation to a Variable Fractional Order. Integral Transforms and Special Functions, 1, 277-300. http://dx.doi.org/10.1080/10652469308819027
- 7. Ross, B. and Samko, S. (1995) Fractional Integration Operator of Variable Order in the Holder Spaces . International Journal of Mathematics and Ma-thematical Sciences, 18, 777-788. http://dx.doi.org/10.1155/S0161171295001001
- 8. Coimbra, C.F.M. (2003) Mechanica with Variable-Order Differential Operators. Annalen der Physik, 12, 692-703. http://dx.doi.org/10.1002/andp.200310032
- 9. Copper, G.R.J. and Rown, D.R.C. (2004) Filtering Using Variable Order Vertical Derivatives. Computers and Geosciences, 30, 455-459. http://dx.doi.org/10.1016/j.cageo.2004.03.001
- 10. Tseng, C.C. (2006) Design of Variable and Adaptive Fractional Order FIR Differentiators. Signal Processing, 86, 2554-2566. http://dx.doi.org/10.1016/j.sigpro.2006.02.004
- 11. Chen, C.M., Liu, F., Anh, V. and Turner, I. (2010) Numerical Schemes with High Spatial Accuracy for a Variable- Order Anomalous Subdiffusion Equation. SIAM Journal on Scientific Computing, 32, 1740-1760. http://dx.doi.org/10.1137/090771715
- 12. Chen, C.M., Liu, F., Anh, V. and Turner, I. (2011) Numerical Simula-tion for the Variable-Order Galilei Invariant Advection Diffusion Equation with a Nonlinear Source Term. Applied Mathematics and Computation, 217, 5729-5742. http://dx.doi.org/10.1016/j.amc.2010.12.049
- 13. Chen, C.M., Liu, F., Turner, I., Anh, V. and Chen, Y. (2013) Numerical Approximation for a Variable-Order Nonlinear Reaction-Subdiffusion Equation. Numerical Algorithms, 63, 265-290. http://dx.doi.org/10.1007/s11075-012-9622-6
- 14. Zhang, H., Liu, F., Phanikumar, M.S. and Meer-schaert, M.M. (2013) A Novel Numerical Method for the Time Variable Fractional Order Mobile-Immobile Advec-tion-Dispersion Model. Computers and Mathematics with Applications, 66, 693-701. http://dx.doi.org/10.1016/j.camwa.2013.01.031
- 15. 马维元, 张海东, 邵亚斌. 非线性变阶分数阶扩散方程的全隐差分格式[J]. 山东大学学报(自然科学版), 2013, 48(2): 93-97.
- 16. 马亮亮, 刘冬兵. Coimbra变时间分数阶扩散方程–波动方程的新隐式差分法[J]. 西南师范大学学报(自然科学版), 2015, 40(3): 25-31.
- 17. Cheng, J., Nakagawa, J., Yamamoto, M. and Yamazaki, T. (2009) Uniqueness in an Inverse Problem for a One- Dimensional Fractional Diffusion Equation. Inverse Problems, 25, Article ID: 115002. http://dx.doi.org/10.1088/0266-5611/25/11/115002
- 18. Liu, J.J. and Yamamoto, M. (2010) A Backward Problem for the Time-Fractional Diffusion Equation. Applicable Analysis, 89, 1769-1788. http://dx.doi.org/10.1080/00036810903479731
- 19. Sakamoto, K. and Yamamoto, M. (2011) Initial Val-ue/Boundary Value Problems for Fractional Diffusion-Wave Equations and Applications to Some Inverse Problems. Journal of Mathematical Analysis and Applications, 382, 426-447. http://dx.doi.org/10.1016/j.jmaa.2011.04.058
- 20. Yamamoto, M. and Zhang, Y. (2012) Conditional Stability in Determining a Zeroth-Order Coefficient in a Half-Order Fractional Diffusion Equation by a Carleman Estimate. Inverse Problems, 28, Article ID: 105010. http://dx.doi.org/10.1088/0266-5611/28/10/105010
- 21. Wei, T. and Zhang, Z.Q. (2013) Reconstruction of a Time-Dependent Source Term in a Time-Fractional Diffusion Equation. Engineering Analysis with Boundary Elements, 37, 23-31. http://dx.doi.org/10.1016/j.enganabound.2012.08.003
- 22. Li, G.S., Zhang, D.L., Jia, X.Z. and Yamamoto, M. (2013) Simultaneous Inversion for the Space-Dependent Diffusion Coefficient and the Fractional Order in the Time-Fractional Diffusion Equation. Inverse Problems, 29, Article ID: 065014. http://dx.doi.org/10.1088/0266-5611/29/6/065014
- 23. 贾现正, 张大利, 李功胜, 池光胜, 李慧玲. 空间–时间分数阶变系数对流扩散方程微分阶数的数值反演[J]. 计算数学, 2014, 36(2): 113-132.
- 24. Jin, B.T. and Rundell, W. (2015) A Tutorial on Inverse Problems for Anomalous Diffusion Processes. Inverse Problems, 31, Article ID: 035003. http://dx.doi.org/10.1088/0266-5611/31/3/035003
- 25. Li, G.S., Gu, W.J. and Jia, X.Z. (2012) Numerical Inversions for Space-Dependent Diffusion Coefficient in the Time Fractional Diffusion Equation. Journal of Inverse and Ill-Posed Problems, 20, 339-366. http://dx.doi.org/10.1515/jip-2011-0012
- 26. Zhang, D.L., Li, G.S., Jia, X.Z. and Li, H.L. (2013) Simultaneous Inversion for Space-Dependent Diffusion Coefficient and Source Magnitude in the Fractional Diffusion Equation. Journal of Mathematics Research, 5, 65-78. http://dx.doi.org/10.5539/jmr.v5n2p65
