Advances in Applied Mathematics
Vol.05 No.01(2016), Article ID:16964,7
pages
10.12677/AAM.2016.51004
Positive Solutions for a Third-Order Three-Point Singular Boundary Value Problem
Hongping Wu
College of Mathematics and Statistics, Northwest Normal University, Lanzhou Gansu

Received: Feb. 1st, 2016; accepted: Feb. 20th, 2016; published: Feb. 23rd, 2016
Copyright © 2016 by author and Hans Publishers Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/



ABSTRACT
This paper is concerned with the following nonlinear third-order three-point boundary value problem
 where
where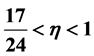 , the nonlinear term may be singular at
, the nonlinear term may be singular at 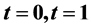 and
and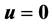 . By using fixed- point theorem in cone, the existence of one or two or n positive solutions is obtained with the weaker conditions.
. By using fixed- point theorem in cone, the existence of one or two or n positive solutions is obtained with the weaker conditions.
Keywords:Third-Order Three-Point Boundary Value Problem, Singular, Positive Solutions, Fixed-Point Theorem

一类奇异三阶三点边值问题正解的存在性
吴红萍
西北师范大学数学与统计学院,甘肃 兰州

收稿日期:2016年2月1日;录用日期:2016年2月20日;发布日期:2016年2月23日

摘 要
讨论非线性三阶三点边值问题

其中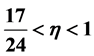 ,非线性项允许在
,非线性项允许在 及
及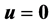 处奇异,利用锥上的不动点定理在较弱的条件下得到了上述边值问题至少存在一个、两个、n个正解的存在性结果。
处奇异,利用锥上的不动点定理在较弱的条件下得到了上述边值问题至少存在一个、两个、n个正解的存在性结果。
关键词 :三阶三点边值问题,奇异,正解,不动点定理

1. 引言
本文主要研究以下三阶三点奇异边值问题
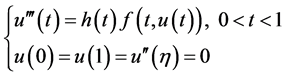 (1)
(1)
其中 ,更一般地,
,更一般地,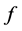 允许在
允许在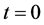 和(或)
和(或)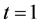 或
或 处奇异。
处奇异。
三阶常微分方程起源于应用数学和物理的各种领域,例如,带有固定或变化横截面的屈曲梁的挠度、三层梁、电磁波、地球引力吹积的涨潮等[1] 。最近常微分方程三点边值问题受到了人民的广泛关注,详见文献 [2] - [7] ,特别地,Alex P等在文 [8] 首次讨论了问题(1)的正解,通过对相应Green函数的深入讨论,得到了问题(1)至少有一个正解的存在性结果,重要的是该结果表明尽管Green函数并不完全是正的,问题的解却是严格正的。文 [9] 中,本人讨论了问题(1)两个正解的存在性结果。
受此启发,本文在更弱的条件下,继续讨论问题(1)的正解,利用Guo-Krasnoselskii不动点定理,笔者的工作表明,只要非线性项 在某些有界集的连续部分
在某些有界集的连续部分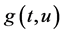 高度适当的情况下,问题(1)必定存在一个、两个、n个正解。
高度适当的情况下,问题(1)必定存在一个、两个、n个正解。
2. 预备与引理
本文我们作如下假设:
(H1)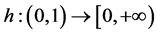 连续且满足
连续且满足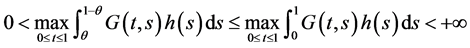 ,其中
,其中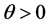 满足
满足 。
。
(H2) 连续。
连续。
(H3) 存在两个连续函数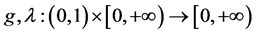 ,使得
,使得 ,
, 。
。
(H4) 是一个非降函数,对于任意的
是一个非降函数,对于任意的 。
。
(H5) 对于任意的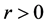 ,
, ,其中
,其中 。
。
本文的工作空间为Banach空间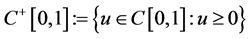 ,其中的范数为
,其中的范数为 。
。
令 。
。
易知 为
为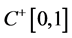 中的锥。
中的锥。
引理1 [8] 边值问题 的Green函数为
的Green函数为
当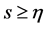 时,
时,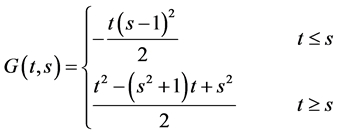
当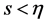 时,
时,
经过简单计算,我们有
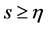 时,
时,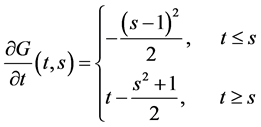 ,
,
 时,
时, ,
,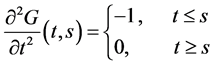
进一步
当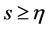 时,
时,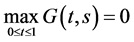 ,
,
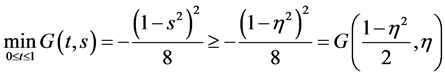 (2)
(2)
当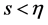 时,
时,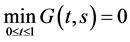
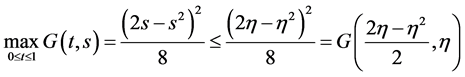 (3)
(3)
因此
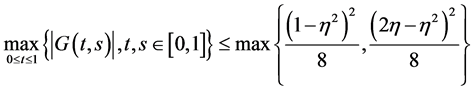 。
。
引理2 [8] 设 是(0,1)上的连续可积函数,满足
是(0,1)上的连续可积函数,满足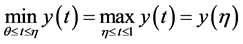 ,则边值问题
,则边值问题
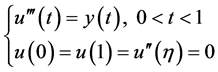 (Ey)
(Ey)
有唯一非负解 。且在
。且在 上是凸的,在
上是凸的,在 上是凹的。
上是凹的。
引理3 [8] 设y如同引理2所述,则边值问题(Ey)的唯一非负解 并且满足
并且满足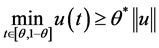 ,其中
,其中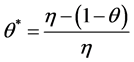 (很显然
(很显然 )。
)。
定义锥 。以及算子
。以及算子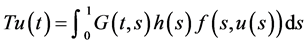 。
。
记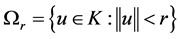 ,
, 。
。
引理4 设 ,则
,则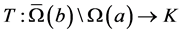 全连续。
全连续。
证明 取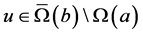 ,则有
,则有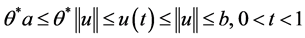 。
。
由(H4),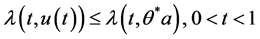 。依(H5),
。依(H5),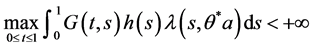 。
。
令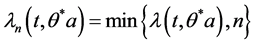 ,则有
,则有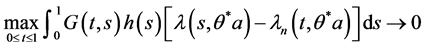 。
。
令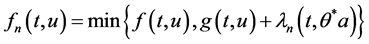 ,则
,则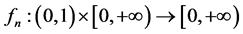 连续。
连续。
定义算子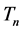 如下:
如下:
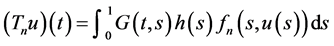
模仿文[3] 中引理3的证明,结合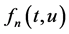 的连续性及Arzela-Ascoli定理,容易验证
的连续性及Arzela-Ascoli定理,容易验证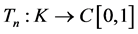 全连续。
全连续。
 。
。
上式表明全连续算子 在集合
在集合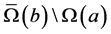 上一致收敛于
上一致收敛于 ,因此
,因此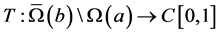 是全连续算子,进一步
是全连续算子,进一步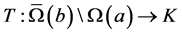 全连续。
全连续。
引理5 [10] 设 是Banach空间,
是Banach空间,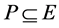 是E中的一个锥,
是E中的一个锥, 是E中的有界开集
是E中的有界开集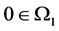 ,
, ,设
,设 全连续,如果满足条件:
全连续,如果满足条件:
1) ;或
;或
2) 
那么,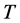 在
在 中必有不动点。
中必有不动点。
3. 主要结果
引入以下两个“高度”函数:
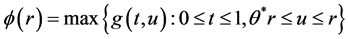 ;
;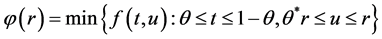 。
。
另记 ;
;
 ,
,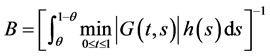 。
。
定理1 假设存在两个正数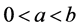 ,使得以下条件成立其一:
,使得以下条件成立其一:
(A1)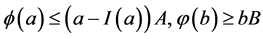 ;
;
(A2)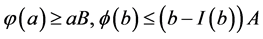 ;
;
则边值问题(1)至少有一个正解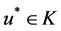 且
且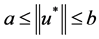 。
。
证明 不失一般性,我们只证明满足(A1)的情形。
如果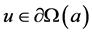 ,则
,则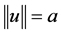 且
且 ,由(H4)和(A1),
,由(H4)和(A1),
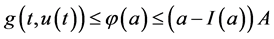 ,
,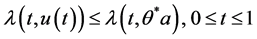 ,进而根据引理
,进而根据引理
 。
。
故
 。 (4)
。 (4)
若 ,则
,则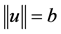 且
且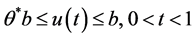 ,因此
,因此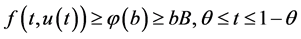 。
。
故 。
。
即
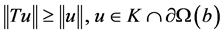 (5)
(5)
依引理4及引理5知,算子 有一个不动点
有一个不动点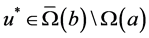 。意即
。意即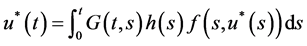 ,
,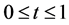 。故有
。故有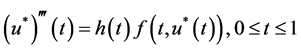 。依引理1,
。依引理1,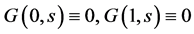 ,
, ,故有
,故有 ,因此
,因此 是问题(1)的一个解,且
是问题(1)的一个解,且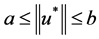 ,另由
,另由 ,知
,知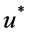 是正的。
是正的。
注记 定理1表明,问题(1)的正解存在性只与非线性项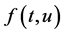 在集合
在集合 边界的特性有关,与
边界的特性有关,与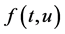 在集合内部的状态无关。
在集合内部的状态无关。
定理2 假设存在三个正数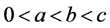 使得以下条件成立其一:
使得以下条件成立其一:
(B1)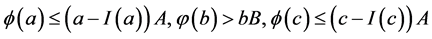 ;
;
(B2) 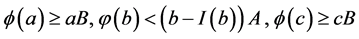
则边值问题(1)至少有两个正解 且
且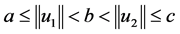 。
。
证明 我们只证条件(B2)的情形。
由条件 ,利用定理1的证明易知,问题(1)至少有一个正解
,利用定理1的证明易知,问题(1)至少有一个正解 ,
,
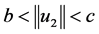 。同样的,利用条件
。同样的,利用条件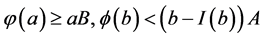 及定理1知,问题(1)还有另一个正解
及定理1知,问题(1)还有另一个正解
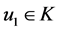 ,
, 。
。
定理3 假设存在四个正数 使得以下条件成立其一:
使得以下条件成立其一:
(C1) ;
;
(C2) 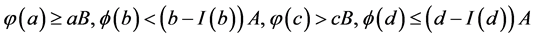
则边值问题(1)至少有三个正解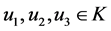 且
且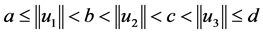 。
。
定理4 假设存在n+1个正数 使得以下条件成立其一:
使得以下条件成立其一:
(D1) 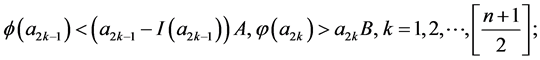
(D2) 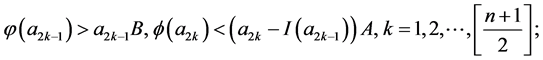
则边值问题(1)至少有n个正解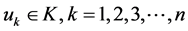 ,且
,且 。(其中
。(其中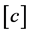 表示
表示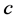 的整数部分)。
的整数部分)。
推论1 假设 (尤其
(尤其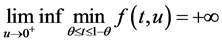 ),存在一个正数
),存在一个正数 使得
使得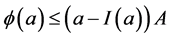 ,则边值问题(1)至少有一个正解
,则边值问题(1)至少有一个正解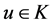 满足
满足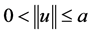 。
。
证明 由于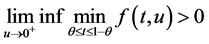 ,故存在
,故存在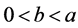 使得
使得 ,
,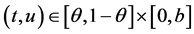 。
。
亦即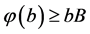 。故依定理1知问题(1)至少有一个正解
。故依定理1知问题(1)至少有一个正解 满足
满足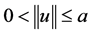 。
。
推论2 假设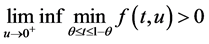 ,存在n个正数
,存在n个正数 ,使得
,使得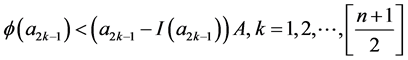 且
且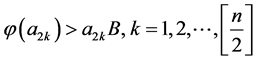 ,则边值问题(1)有n个正解
,则边值问题(1)有n个正解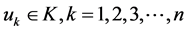 ,满足
,满足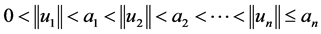 。
。
推论3 假设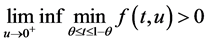 ,且
,且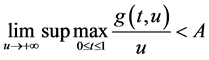 ,则边值问题(1)至少有一个正解。
,则边值问题(1)至少有一个正解。
证明 取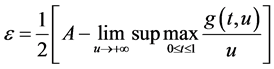 ,则存在
,则存在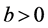 使得
使得
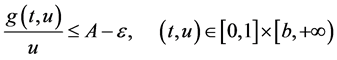
选取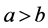 使得
使得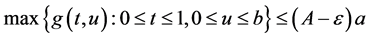 且
且 ,由此知,
,由此知,
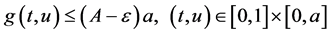
依(H4)及(H5),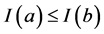 。
。
 。
。
故推论1的条件满足,即问题(1)至少有一个正解。
基金项目
国家自然科学基金(11261053);甘肃省自然科学基金(1308RJZA125)。
文章引用
吴红萍. 一类奇异三阶三点边值问题正解的存在性
Positive Solutions for a Third-Order Three-Point Singular Boundary Value Problem[J]. 应用数学进展, 2016, 05(01): 24-30. http://dx.doi.org/10.12677/AAM.2016.51004
参考文献 (References)
- 1. Gregus, M. (1987) Third Order Linear Differential Equations. Reidel, Dordrecht. http://dx.doi.org/10.1007/978-94-009-3715-4
- 2. Anderson, D.R. (2003) Green’s Function for a Third-Order Generalized Right Focal Problem. Journal of Mathematical Analysis and Applications, 288, 1-14. http://dx.doi.org/10.1016/S0022-247X(03)00132-X
- 3. Sun, Y.P. (2005) Positive Solutions of Singular Third-Order Three-Point Boundary Value Problem. Journal of Mathematical Analysis and Applications, 306, 589-603. http://dx.doi.org/10.1016/j.jmaa.2004.10.029
- 4. Sun, Y.P. (2009) Positive Solutions for Third-Order Three-Point Nonhomogeneous Boundary Value Problem. Applied Mathematics Letters, 22, 45-51. http://dx.doi.org/10.1016/j.aml.2008.02.002
- 5. Anderson, D.R. and Avery, R. (2001) Multiple Positive Solutions to a Third-Order Discrete Flocal Boundary Value Problems. Computers & Mathematics with Applications, 42, 333-340. http://dx.doi.org/10.1016/S0898-1221(01)00158-4
- 6. Kaufmann, E.R. (2003) Positive Solutions of a Three-Point Boundary Value Problem on a Time Scale. Electron. J. Diff. Equa., 82, 1-11.
- 7. Anderson, D.R., Anderson, T. and Kleber, M. (2006) Green’s Function and Existence of Soluyions for a Functional Focal Differential Equations. Electron. J. Diff. Equa., 12, 1-14.
- 8. Palamides, A.P. and Smyrlis, G. (2008) Positive Solutions to a Singular Third-Order Three-Point Boundary Value Problem with an Indefinitely Signed Green’s Function. Nonlinear Analysis, 68, 2104-2118. http://dx.doi.org/10.1016/j.na.2007.01.045
- 9. Wu, H.P. (2011) Multiple Positive Solutions to a Singular Third-Order Three-Point Boundary Value Problem. Annals of Differential Equations, 27, 379-383.
- 10. Guo, D. and Lakshmikantham, V. (1988) Nonlinear Problems in Abstract Cone. Academic Press, San Diego.