Advances in Applied Mathematics
Vol.06 No.03(2017), Article ID:20589,6
pages
10.12677/AAM.2017.63029
The Form of Solution for a Class of Nonlinear Ordinary Differential Equations
Xiaozhen Tao, Yanfeng Guo, Mei Liao, Jielin Chen
School of Sciences, Guangxi University of Sciences and Technology, Liuzhou Guangxi

Received: Apr. 29th, 2017; accepted: May 12th, 2017; published: May 22nd, 2017

ABSTRACT
In this paper, the exact solution of a class of nonlinear ordinary differential equations is solved by using the F-expansion method. Firstly, by using variable transformation, and through the idea of the homogeneous balance method, some forms of solution are given. By application of mathematical software Maple, some solutions are solved combined with the solution of Riccati equation. And forms of the exact solutions of nonlinear ordinary differential equations are obtained.
Keywords:F-Expansion Method, Homogeneous Balance Method, Riccati Equation
某类非线性常微分方程解的形式
陶晓珍,郭艳凤,廖媚,陈杰玲
广西科技大学 理学院,广西 柳州
收稿日期:2017年4月29日;录用日期:2017年5月12日;发布日期:2017年5月22日

摘 要
本论文主要应用F展开法求解某类非线性常微分方程的精确解。首先利用相应自变量变换,再通过齐次平衡法的思想确定方程的某种解的形式,应用数学软件Maple进行求解,再结合相应的Riccati方程的解的表达式,得到了该类非线性常微分方程的精确解的表达形式。
关键词 :F展开法,齐次平衡法,Riccati方程

Copyright © 2017 by authors and Hans Publishers Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/


1. 引言
随着社会经济及计算机技术的飞快发展,微分方程的应用也越来越广泛,求解高阶偏微分方程也出现了多种方法,例如齐次平衡法 [1] [2] 、双线性法 [3] [4] 、F展开法 [5] [6] 等等。
本文主要讨论某类非线性常微分方程的精确解形式。由于上面提到的几种方法是求解偏微分方程精确解的有效方法,本文将利用这些方法的思想来求解某类非线性常微分方程的精确解形式。这里主要通过F展开法来研究某类非线性常微分方程的精确解形式,首先通过相应自变量变换,再通过齐次平衡法的思想确定方程的某种解的形式,应用数学软件Maple进行求解,再结合相应的Riccati方程的解的表达式,得到了该类非线性常微分方程的精确解的表达形式,从而得到了新的结果。
2. 利用F展开法求解某类非线性常微分方程
在流体力学中,一个很重要的方程是Swift-Hohenberg方程
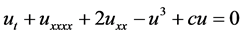 .(2.0.1)
.(2.0.1)
此方程是在讨论Rayleigh-Bénard对流中的不稳定对流现象得到的数学模型 [7] ,其中系数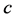 是一个参变量。此方程的精确解形式目前还没有得到很好的解决。本文我们将不考虑时间
是一个参变量。此方程的精确解形式目前还没有得到很好的解决。本文我们将不考虑时间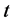 的作用,利用F展开法的思想在参变量
的作用,利用F展开法的思想在参变量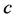 取特殊值的时候得到方程(2.0.2)的
取特殊值的时候得到方程(2.0.2)的
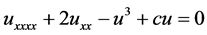 , (2.0.2)
, (2.0.2)
某种精确解形式。
2.1. 求解待定系数的代数方程组
首先进行自变量变换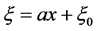 (其中
(其中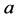 是待定的常数,
是待定的常数, 则为任意的常数),得到相应的常微分方程:
则为任意的常数),得到相应的常微分方程:
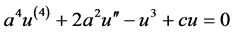 , (2.1.1)
, (2.1.1)
假设常微分方程(2.1.1)解的形式如下:
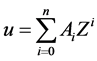 , (2.1.2)
, (2.1.2)
其中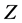 满足Riccati方程
满足Riccati方程
 , (2.1.3)
, (2.1.3)
方程(2.1.3)中的 ,
,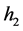 ,
,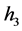 为待定实常数。再根据最高次导数项以及最高次幂非线性项进行齐次平衡,所以我们可以得到
为待定实常数。再根据最高次导数项以及最高次幂非线性项进行齐次平衡,所以我们可以得到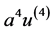 的最高次数为
的最高次数为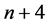 ,
, 最高次数为
最高次数为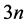 ,所以就有
,所以就有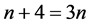 ,解得
,解得 。把
。把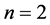 回代到方程(2.1.2)中,得到
回代到方程(2.1.2)中,得到
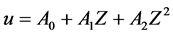 , (2.1.4)
, (2.1.4)
求出对应的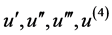 ,再把
,再把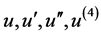 代入方程(2.1.1),且令多项式
代入方程(2.1.1),且令多项式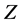 的各项系数都为零,得系数方程组为:
的各项系数都为零,得系数方程组为:

再运用数学软件Maple来求解代数方程组,并去掉一些无意义的解,得到以下六组解:
第一组解为
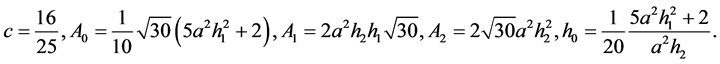
第二组解为
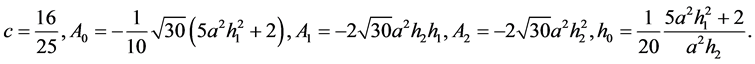
第三组解为
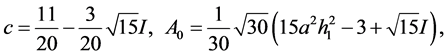
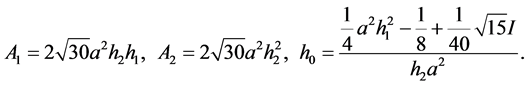
第四组解为
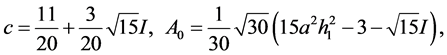
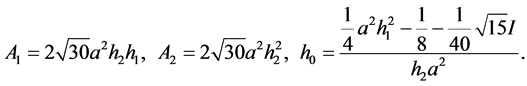
第五组解为
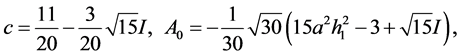
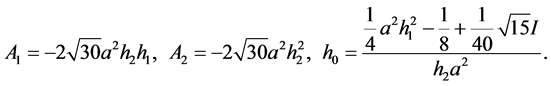
第六组解为
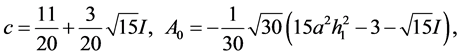
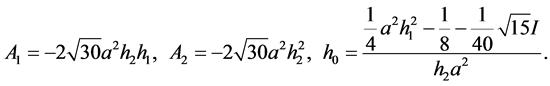
2.2. 分析方程Riccati的解
情况:当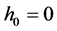 时,方程(2.1.3)简化为:
时,方程(2.1.3)简化为: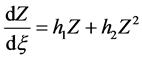 。该方程的解为:
。该方程的解为:
 ,因此,
,因此,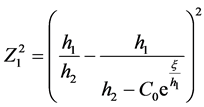 。 (2.2.1)
。 (2.2.1)
情况:当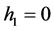 时,方程(2.1.3)简化为
时,方程(2.1.3)简化为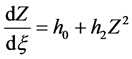 。该方程的解为:
。该方程的解为:
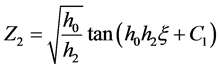 ,因此,
,因此,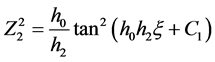 。 (2.2.2)
。 (2.2.2)
情况:当 时,方程(2.1.3)简化为
时,方程(2.1.3)简化为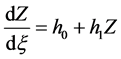 。该方程的解为:
。该方程的解为:
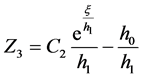 ,因此,
,因此, 。 (2.2.3)
。 (2.2.3)
根据上述所讨论的三种情况,因而式子(2.2.1)、(2.2.2)、(2.2.3)便是方程(2.1.3)根据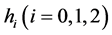 的取值情况所得到的不同的精确解。
的取值情况所得到的不同的精确解。
2.3. 讨论该类非线性常微分方程的解
将2.1节求得的各参数的解组以及2.2节所求的一阶常微分方程的通解代入方程(2.1.4)中,就得到该类非线性常微分方程(2.0.2)的精确解。
情况:当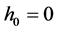 时,方程(2.1.3)简化为
时,方程(2.1.3)简化为 ,方程(2.1.1)的解为
,方程(2.1.1)的解为
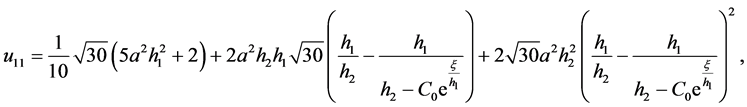
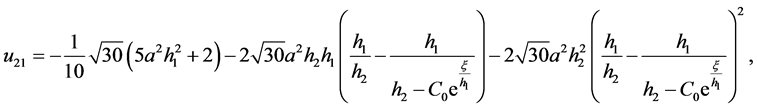


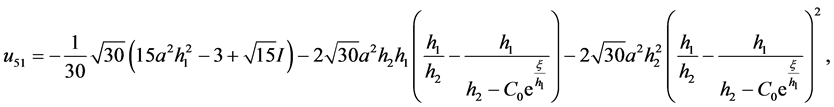

情况:当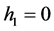 时,方程(2.1.3)简化为
时,方程(2.1.3)简化为 ,得方程(2.1.1)的解为
,得方程(2.1.1)的解为
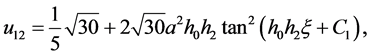
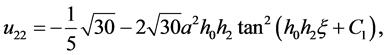
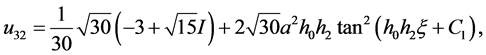
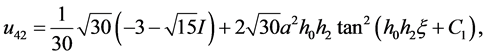
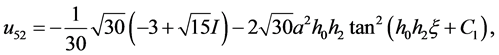
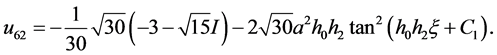
情况:当 时,方程(2.1.3)简化为
时,方程(2.1.3)简化为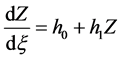 ,得方程(2.1.1)的解为
,得方程(2.1.1)的解为



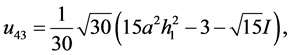
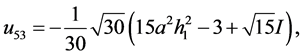

以上所得到的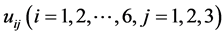 表示第
表示第 组解中第
组解中第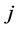 种情况的该类非线性常微分方程(2.0.2)的精确解。
种情况的该类非线性常微分方程(2.0.2)的精确解。
基金项目
本项目由国家自然科学基金(No. 11301097),广西壮族自治区大学生创新创业训练计划项目(No. 201610594124)资助。
文章引用
陶晓珍,郭艳凤,廖媚,陈杰玲. 某类非线性常微分方程解的形式
The Form of Solution for a Class of Nonlinear Ordinary Differential Equations[J]. 应用数学进展, 2017, 06(03): 243-248. http://dx.doi.org/10.12677/AAM.2017.63029
参考文献 (References)
- 1. Wang, M.L. (1995) Solitary Wave Solutions for Variant Boussinesq Equations. Physics Letters A, 199, 169-172. https://doi.org/10.1016/0375-9601(95)00092-H
- 2. Swift, J.B. and Hohenberg, P.C. (1977) Hydrodynamic Fluctuations at the Convective Instability. Physical Review A, 15, 319-328. https://doi.org/10.1103/PhysRevA.15.319
- 3. Yang, L., Zhu, Z.G. and Wang, Y.H. (1999) Exact Solutions of Nonlinear Equations. Physics Letters A, 260, 55-59. https://doi.org/10.1016/S0375-9601(99)00482-X
- 4. Cao, D.B. (2002) New Exact Solutions for a Class of Nonlinear Coupled Differential Equations. Physics Letters A, 296, 27-33. https://doi.org/10.1016/S0375-9601(02)00151-2
- 5. Ruan, H.Y. and Chen, Y.X. (2003) Soliton Interactions of Integrable Models. Chaos, Solitons and Fractals, 17, 929- 939. https://doi.org/10.1016/S0960-0779(02)00576-3
- 6. 何宝钢, 徐昌智, 张解放. (2+1)维非线性KdV方程的新孤子结构[J]. 物理学报, 2005, 54(12): 5525-5529.
- 7. 刘常福. Davey-Stewartson I方程的精确波类解[D]: [硕士学位论文]. 云南: 云南大学, 2006.