Journal of Aerospace Science and Technology
Vol.05 No.01(2017), Article ID:20096,10
pages
10.12677/JAST.2017.51004
Optimal Attitude Control of Three-Axis Satellite Based on Approximate Dynamic Programming
Mingze Wang1, Xinsheng Ge2
1College of Automation Engineering, Beijing Information Science and Technology University, BISTU, Beijing
2College of Applied Science, Beijing Information Science and Technology University, BISTU, Beijing

Received: Mar. 10th, 2017; accepted: Mar. 28th, 2017; published: Mar. 31st, 2017

ABSTRACT
The optimal attitude trajectory planning of three-axis satellite using approximate dynamic programming (ADP) method is discussed. Firstly, the dynamic and kinematic equations of the three-axis satellite are used, and for given initial and final attitudes, the performance to be optimized is selected as minimizing the rest-to-rest maneuver energy. On grounds of adaptive dynamic programming structure, critic network and action network are used to approximate performance index function and control variables respectively, and Runge-Kutta method to solve the state variables. Besides, a concrete expression of the utility function is provided which is suitable for this kind of problem. The simulation results show that the proposed algorithm satisfies the constraints well and can be used on-line with its small computational amount and low computational complexity.
Keywords:Attitude Control, Approximate Dynamic Programming, Three-Axis Satellite, Optimal Control, Neural Network
基于近似动态规划的三轴卫星姿态最优控制
王明泽1,戈新生2
1北京信息科技大学自动化学院,北京
2北京信息科技大学理学院,北京
收稿日期:2017年3月10日;录用日期:2017年3月28日;发布日期:2017年3月31日

摘 要
应用近似动态规划方法解决三轴卫星姿态最优轨迹规划问题,首先使用三轴卫星的动力学和运动学模型,对于给定的始末姿态,选取姿态机动能量消耗最少作为待优化的性能指标。文中根据自适应动态规划结构,分别利用评价网络来近似性能指标函数和执行网络来逼近控制变量,龙格库塔法求解状态变量,并给出了适合该类问题的一种效用函数的具体表达式。仿真结果表明应用近似动态规划解得的三轴卫星最优轨迹,能够较好地满足各种约束条件,而且计算精度高、速度快,具有很好的实时性。
关键词 :姿态控制,近似动态规划,三轴卫星,最优控制,神经网络

Copyright © 2017 by authors and Hans Publishers Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/


1. 引言
从1957人类第一颗卫星上天到最近我国天宫二号载人航天的成功发射,航天技术一直是世界各国重点发展的尖端技术。经过几十年的快速发展,航天技术日臻完善,卫星也因此广泛应用在通信,导航,气象,军事等各个领域。在卫星执行空间任务的过程中,经常会需要使姿态从某一状态旋转到另一状态,这要求卫星姿态控制系统必须根据初末端状态给出期望的控制力矩指令。本文根据三轴卫星姿态机动消耗的能量最少作为待优化的目标提出了近似动态规划方法求解该优化问题。
近似动态规划结合了动态规划、强化学习、神经网络等方面的内容,是一种智能优化控制方法。因此近似的方法早在1950年后期就被认可,近似动态规划是一类启发技术,其通过搜索合适的近似来求解代价函数。特别是,近似动态规划方法应用强化学习的思想来获得代价函数的在线近似而不需要使用系统动态的知识。近年来,国际控制与智能计算领域的许多学者对近似动态规划进行了研究,但多数是关于算法和仿真的研究,也有一些文献谈到近似动态规划的理论问题,如收敛性和最优性等,但主要是针对线性系统和特殊非线性系统。文献 [1] 按照ADP的结构变化、算法的发展和应用三个方面介绍ADP方法,总结了当前ADP方法的研究成果,并对该领域仍需解决的问题和未来的发展方向作了进一步的展望;文献 [2] 提出了一种基于ADP方法的有限时域最优控制方法,该方法通过迭代求解最优控制策略,使得系统的代价函数在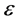 范围内无限接近其最优值,并可以求出最优控制步数;文献 [3] 展示了基于ADP方法的在线无模型自适应评价策略求解对于线性系统的离散时间和连续时间域的最优控制问题,并用在电力系统的仿真验证了两种算法的有效性;文献 [4] 提出的不确定连续时间非线性多项式系统GADP方法,它不需要使用神经网络去近似,并能通过在线学习得到全局自适应次优稳定的控制策略;文献 [5] 对连续时间线性系统的无模型在线ADP求解无限范围线性二次型最优控制;文献 [6] 通过2D平面机器人举例说明ADHDP强化控制;文献 [7] 提出了两个无模型ADP方法,但是需要用到值函数对状态的导数信息;文献 [8] 提出ADP方法用于一类非线性系统有限范围最优跟踪控制,文中用到迭代HDP算法;文献 [9] 提出了迭代自适应算法用于带有约束输入的未知非线性离散时间系统的最优控制,文中用到一个神经网络辨识未知动态系统,两个基于GDHP方法的神经网络逼近性能指标及其导数和控制律;文献 [10] 介绍了通过神经网络实现的基于ADP的自学习控制方法,并从强化学习与自适应评价设计两个方面研究了ADP的发展状况;文献 [11] 提出新型策略迭代方法用于找出带有完全未知系统动态的线性连续时间系统的在线自适应最优控制器,该方法根据状态与输入的在线信息,利用ADP技术迭代求解代数黎卡提方程;文献 [12] 提出对于一类未知非线性动态系统使用SN-DHP技术的神经最优控制,该方法需要先辨识未知的动态系统,然后采用单网络DHP求解最优控制问题;文献 [13] 提出针对离散时间HJB系统的基于三角形隶属度函数的模糊HDP算法的收敛性分析与应用;Jennie Si在通过联系与强化的在线学习控制中提了神经动态规划方法,并在讨论与总结中提到自组织映射(SOM)网络在解决带有多变量的复杂系统可以降低计算复杂度 [14] ;魏庆来等提出了基于策略迭代的稳定的Q学习算法实现非线性神经最优跟踪控制 [15] 。国内关于三轴卫星姿态控制的研究很早就开始了,文献 [16] 对卫星动力学、卫星姿态控制等进行了深入研究;文献 [17] [18] 对三轴稳定卫星分别采用了Legendre伪谱法和Gauss伪谱法进行姿态机动最优控制;文献 [19] 介绍了控制参数辨识RBF神经网络滑模自适应控制。
范围内无限接近其最优值,并可以求出最优控制步数;文献 [3] 展示了基于ADP方法的在线无模型自适应评价策略求解对于线性系统的离散时间和连续时间域的最优控制问题,并用在电力系统的仿真验证了两种算法的有效性;文献 [4] 提出的不确定连续时间非线性多项式系统GADP方法,它不需要使用神经网络去近似,并能通过在线学习得到全局自适应次优稳定的控制策略;文献 [5] 对连续时间线性系统的无模型在线ADP求解无限范围线性二次型最优控制;文献 [6] 通过2D平面机器人举例说明ADHDP强化控制;文献 [7] 提出了两个无模型ADP方法,但是需要用到值函数对状态的导数信息;文献 [8] 提出ADP方法用于一类非线性系统有限范围最优跟踪控制,文中用到迭代HDP算法;文献 [9] 提出了迭代自适应算法用于带有约束输入的未知非线性离散时间系统的最优控制,文中用到一个神经网络辨识未知动态系统,两个基于GDHP方法的神经网络逼近性能指标及其导数和控制律;文献 [10] 介绍了通过神经网络实现的基于ADP的自学习控制方法,并从强化学习与自适应评价设计两个方面研究了ADP的发展状况;文献 [11] 提出新型策略迭代方法用于找出带有完全未知系统动态的线性连续时间系统的在线自适应最优控制器,该方法根据状态与输入的在线信息,利用ADP技术迭代求解代数黎卡提方程;文献 [12] 提出对于一类未知非线性动态系统使用SN-DHP技术的神经最优控制,该方法需要先辨识未知的动态系统,然后采用单网络DHP求解最优控制问题;文献 [13] 提出针对离散时间HJB系统的基于三角形隶属度函数的模糊HDP算法的收敛性分析与应用;Jennie Si在通过联系与强化的在线学习控制中提了神经动态规划方法,并在讨论与总结中提到自组织映射(SOM)网络在解决带有多变量的复杂系统可以降低计算复杂度 [14] ;魏庆来等提出了基于策略迭代的稳定的Q学习算法实现非线性神经最优跟踪控制 [15] 。国内关于三轴卫星姿态控制的研究很早就开始了,文献 [16] 对卫星动力学、卫星姿态控制等进行了深入研究;文献 [17] [18] 对三轴稳定卫星分别采用了Legendre伪谱法和Gauss伪谱法进行姿态机动最优控制;文献 [19] 介绍了控制参数辨识RBF神经网络滑模自适应控制。
以上对于三轴卫星的控制方法中的伪谱法是基于插值近似的,插值点的个数以及初始值的选择都会对最终结果产生较大影响;基于控制参数辨识的RBF神经网络滑模自适应控制,用参数辨识的方法在线调整控制参数,使系统按照设定的模态运行,所谓的自适应是向给定模型逼近已达到某种性能指标。关于近似动态规划在卫星姿态最优控制方面的应用还没有人研究,近似动态规划则是通过神经网络学习逼近最优控制的,不需要按照给定的控制模型去近似,是一种智能的控制方法。本文通过近似动态规划方法求解三轴卫星姿态机动问题,使用增广状态方程将三轴卫星的动力学方程与运动学方程合并为一个状态方程,在此基础上分析了卫星的三轴姿态机动与单轴姿态机动的近似动态规划最优控制并与同为智能算法的遗传算法的结果进行比较。
2. 三轴卫星姿态机动最优控制问题
2.1. 卫星动力学方程及卫星运动学方程
应用修正罗德里格参数与方向余弦矩阵的关系式,可得修正罗德里格参数描述方式下的卫星运动方程 [17] 。
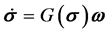 (1)
(1)
其中
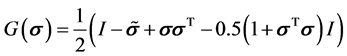
式中 为欧拉转角,
为欧拉转角,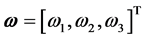 为姿态相对惯性参考坐标系的转速,
为姿态相对惯性参考坐标系的转速,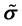 为斜对称阵。
为斜对称阵。
卫星姿态动力学方程
 (2)
(2)
式中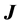 为三轴卫星的惯量矩阵,
为三轴卫星的惯量矩阵,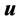 为外部作用力矩,
为外部作用力矩,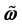 为斜对称阵。
为斜对称阵。
2.2. 最优控制问题的一般形式
最优控制问题的三要素是,系统的运动方程,物理约束条件,性能指标。根据最优控制问题的三要素,可以将一个一般的最优控制问题描述如下
被控系统的状态方程及初始条件为
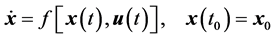 (3)
(3)
其中, 为状态向量,
为状态向量, 为状态向量的容许集;
为状态向量的容许集;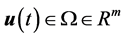 为控制向量,
为控制向量,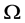 为控制向量的容许集。试确定容许的最优控制
为控制向量的容许集。试确定容许的最优控制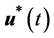 和最优状态轨迹
和最优状态轨迹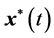 ,使得系统实现从初始状态
,使得系统实现从初始状态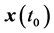 到目标
到目标
 (4)
(4)
的转移,同时使得性能指标
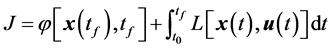 (5)
(5)
达到极值。
2.3. 卫星姿态机动能量最优控制问题的数学描述
针对2.1节描述的卫星动力学及卫星运动学方程,结合2.2节给出的最优控制问题的一般形式,此处给出三轴稳定卫星姿态机动的能量最优控制问题的一般形式
针对三轴稳定卫星的系统方程
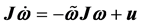 (6)
(6)
 (7)
(7)
初始条件
终端约束
性能指标
 (8)
(8)
控制约束
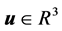
由于上述最优控制问题,具有强非线性和耦合性,无法通过极小值原理或HJB方程等方法求得解析解,因此需要通过数学方法变换为一类参数优化问题,再通过优化算法求解。
3. 近似动态规划方法
3.1. 近似动态规划方法概述
近似动态规划的目标是为动态系统提供一个控制信号的集合,随着时间来最大化或最小化效用函数。该效用函数可以是总能量、成本效率、轨迹的平滑性等。本文采用ADHDP近似动态规划方法,为了方便说明,我们假设符号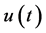 表示控制信号,
表示控制信号,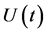 表示效用函数,它一般是系统状态的函数。执行网络用来提供控制信号以最大化或最小化效用函数,这一目标是通过执行网络内部的权值调整实现的。而这一调整又是通过各种信号的反向传播完成的。在每一步迭代中,都有前馈与反馈成分。在前馈过程中,执行网络输出一系列控制信号,而其内部权值的调整是通过反馈过程实现的。换言之,ADHDP的应用包括两个迭代过程,1) 训练评价网络来学习与控制信号集合相应的效用函数;2) 训练执行网络来生成控制信号集合。ADHDP是动态规划的近似实现,通过迭代逼近动态规划的真实解,因此可以逐步靠近非线性系统的最优解。其基本思想是应用函数近似结构近似性能指标函数与控制策略,其最终目标是满足最优性原理以获得最优控制与最优性能指标,有效解决复杂非线性最优控制问题 [12] 。
表示效用函数,它一般是系统状态的函数。执行网络用来提供控制信号以最大化或最小化效用函数,这一目标是通过执行网络内部的权值调整实现的。而这一调整又是通过各种信号的反向传播完成的。在每一步迭代中,都有前馈与反馈成分。在前馈过程中,执行网络输出一系列控制信号,而其内部权值的调整是通过反馈过程实现的。换言之,ADHDP的应用包括两个迭代过程,1) 训练评价网络来学习与控制信号集合相应的效用函数;2) 训练执行网络来生成控制信号集合。ADHDP是动态规划的近似实现,通过迭代逼近动态规划的真实解,因此可以逐步靠近非线性系统的最优解。其基本思想是应用函数近似结构近似性能指标函数与控制策略,其最终目标是满足最优性原理以获得最优控制与最优性能指标,有效解决复杂非线性最优控制问题 [12] 。
3.2. 近似动态规划方法结构
状态取增广形式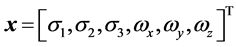 ,控制变量
,控制变量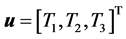 ,根据三轴卫星的动力学方程(6)与运动学方程(7)可以得到状态方程的增广形式。令
,根据三轴卫星的动力学方程(6)与运动学方程(7)可以得到状态方程的增广形式。令
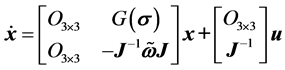 (9)
(9)
上式具有如下形式
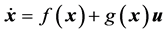 (10)
(10)
其中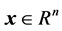 是系统状态,
是系统状态,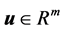 是控制输入。
是控制输入。
用神经网络构造评价网络如式(10)与执行网络如式(11)
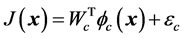 (11)
(11)
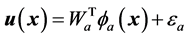 (12)
(12)
其中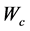 和
和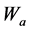 分别是评价网络与执行网络的神经网络权值,
分别是评价网络与执行网络的神经网络权值,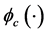 和
和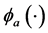 是神经网络的激活函数,
是神经网络的激活函数,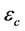 和
和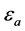 是神经网络的近似误差。为讨论评价网络的权值更新算法,定义评价网络的误差如下
是神经网络的近似误差。为讨论评价网络的权值更新算法,定义评价网络的误差如下
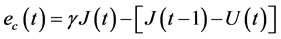 (13)
(13)
其中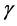 为折扣因子
为折扣因子 ,
, 。需要最小化的评价网络中的目标函数是
。需要最小化的评价网络中的目标函数是
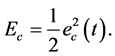 (14)
(14)
评价网络的权值更新规则是基于梯度的自适应算法表示为
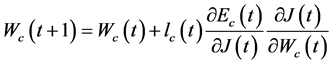 (15)
(15)
其中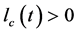 是评价网络在时间
是评价网络在时间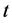 时的学习率,它通常会随着时间递减到一个较小的值,
时的学习率,它通常会随着时间递减到一个较小的值,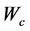 是评价网络的权值向量。
是评价网络的权值向量。
调节执行网络的原理是间接反向传播期望的终端目标和评价网络近似函数的误差。在执行网络中,以测得状态用作网络的输入,以产生的控制作为网络的输出。执行网络的权值更新形式如下
 (16)
(16)
执行网络的权值更新用来最小化如下的性能指标测量
 (17)
(17)
权值更新算法与评价网络的权值更新相似,基于梯度下降规则
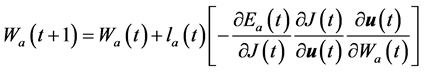 (18)
(18)
其中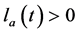 是评价网络在时间
是评价网络在时间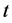 时的学习率,它通常会随着时间递减到一个较小的值,
时的学习率,它通常会随着时间递减到一个较小的值,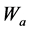 是评价网络的权值向量。
是评价网络的权值向量。
对于动态系统式(10),相应的代价函数如式(8),相应的哈密顿函数为
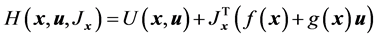 (19)
(19)
其中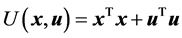 ,
,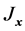 为代价函数
为代价函数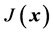 对
对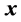 的偏导数。当问题的控制策略和代价函数均取最优时,满足HJB方程,从而
的偏导数。当问题的控制策略和代价函数均取最优时,满足HJB方程,从而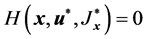 。
。
评价网络的实际输出为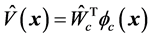 将其带入哈密顿函数(19),可得
将其带入哈密顿函数(19),可得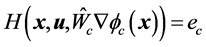 。评价网络训练的目标就是使得
。评价网络训练的目标就是使得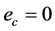 ,使得评价网络的输出值能够逼近代价函数的最优值。控制网的实际输出表示为
,使得评价网络的输出值能够逼近代价函数的最优值。控制网的实际输出表示为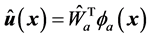 ,执行网络的目标就是使得执行网络的实际输出逼近评价网络输出决定的近似最优控制策略
,执行网络的目标就是使得执行网络的实际输出逼近评价网络输出决定的近似最优控制策略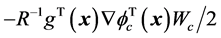 ,其中
,其中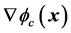 是
是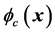 对
对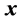 的偏导数。定义控制网络的实际输出与最优控制二者之差等于
的偏导数。定义控制网络的实际输出与最优控制二者之差等于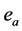 ,执行网络的目标就是使
,执行网络的目标就是使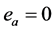 。基于上述思想设计评价网络和执行网络的权值更新规则,使得评价网络和执行网络的权值能够同步更新 [1] 。
。基于上述思想设计评价网络和执行网络的权值更新规则,使得评价网络和执行网络的权值能够同步更新 [1] 。
3.3. 近似动态规划算法步骤
1) 初始化执行网络与评价网络的神经网络的权值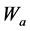 、
、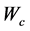 ,阈值
,阈值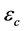 、
、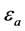 ,以及神经网络学习率
,以及神经网络学习率 、
、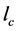 ,定义折扣因子
,定义折扣因子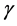 的值。
的值。
2) 读取三轴卫星系统的状态并将其输入到执行网络,计算输出控制动作。
3) 将当前的状态与执行网络输出的控制动作输入被控对象,通过被控对象状态方程获得下一阶段的状态。
4) 将状态、控制输入到评价网络,获得评价网络输出。
5) 将下一时刻的状态输入到执行网络输出下一时刻的控制动作。
6) 将新的状态、控制输入到评价网络,得到评价网络下一时刻的输出。
7) 求解评价网络函数误差值,并依据ADHDP算法流程,依次训练评价网络的权值。
8) 求解执行网络函数误差值,并依据ADHDP算法流程,依次训练执行网络的权值。
9) 循环第2)至第8)步,直到达到最大训练次数或满足误差条件则仿真结束。
4. 仿真实例
仿真实验1:设定三轴卫星只有第一个轴转动,卫星从姿态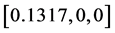 回到
回到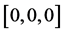 ,其它两个轴初始姿态与终端姿态保持不变,并且初始角速度与终端角速度为0。表1为相关参数列表:
,其它两个轴初始姿态与终端姿态保持不变,并且初始角速度与终端角速度为0。表1为相关参数列表:
Table 1. Single axis maneuver simulation parameter list [18]
表1. 单轴机动仿真参数列表 [18]
对动力学方程式(2)分析可知,由于
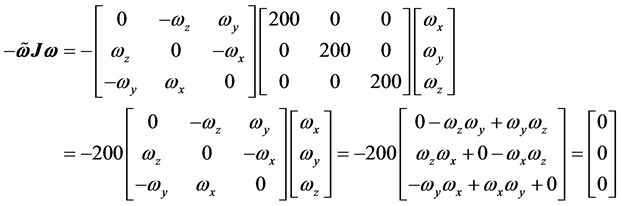
于是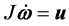 即
即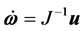 。
。
根据状态方程式(1)式(2)及上表中初始状态可得
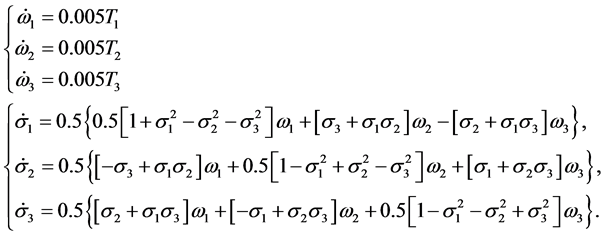
上面的状态方程可以写成如下的离散化形式

当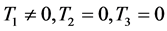 时有
时有
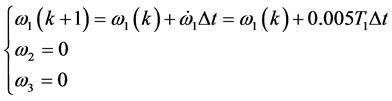
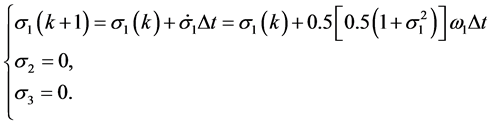
由上面推导可知,可以用单轴力矩控制去实现单轴机动。为检验近似动态规划方法的性能,用遗传算法模拟的bang-bang控制作为对比。利用遗传算法模拟bang-bang控制20步,步长1.02 S,结果如图1(a)~(c)中虚线所示。采用近似动态规划算法,设迭代ADP算法的误差界为 ,在时间
,在时间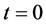 时开始执行该算法,我们选择三层前馈神经网络作为执行网络与评价网络,其结构分别为6-12-3,9-12-1,两个神经网络的权值随机初始化在[−1,1]之间,训练评价网络与执行网络20次迭代,每次迭代1000个训练步,确保达到给定误差界
时开始执行该算法,我们选择三层前馈神经网络作为执行网络与评价网络,其结构分别为6-12-3,9-12-1,两个神经网络的权值随机初始化在[−1,1]之间,训练评价网络与执行网络20次迭代,每次迭代1000个训练步,确保达到给定误差界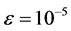 ,在训练过程中
,在训练过程中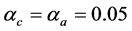 ,仿真结果如图1(a)~(c)中实线所示。在图1中由于只有单轴运动,第2,3轴力矩、角速度、角度都为0,因此没有标注。通过两种方法的对比可以看到,ADHDP可以达到近似Bang-Bang控制的效果。
,仿真结果如图1(a)~(c)中实线所示。在图1中由于只有单轴运动,第2,3轴力矩、角速度、角度都为0,因此没有标注。通过两种方法的对比可以看到,ADHDP可以达到近似Bang-Bang控制的效果。
仿真实验2:设定三轴卫星三个轴都需要转动,卫星从姿态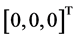 到
到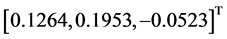 ,并且初始角速度与终端角速度为0。表2为相关参数列表:
,并且初始角速度与终端角速度为0。表2为相关参数列表:

 (a) (b)
(a) (b)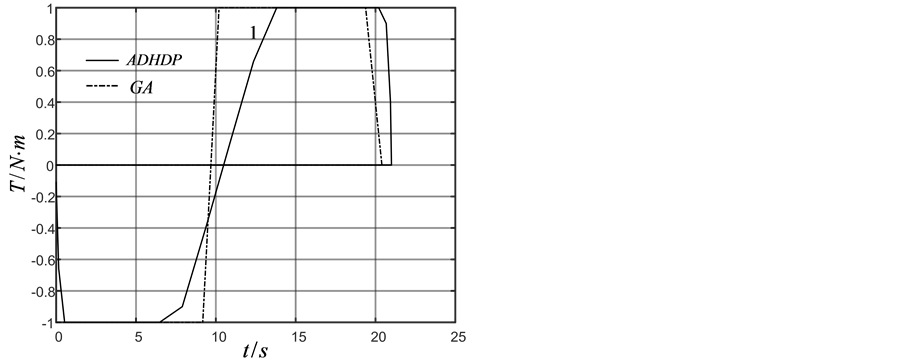 (c)
(c)
Figure 1. (a) Attitude angle; (b) Angle velocity; (c) Curve: Control torque
图1. (a) 姿态角度;(b) 角速度;(c)控制力矩
Table 2. Three axis maneuver simulation parameter list [18]
表2. 三轴机动仿真参数列表 [18]
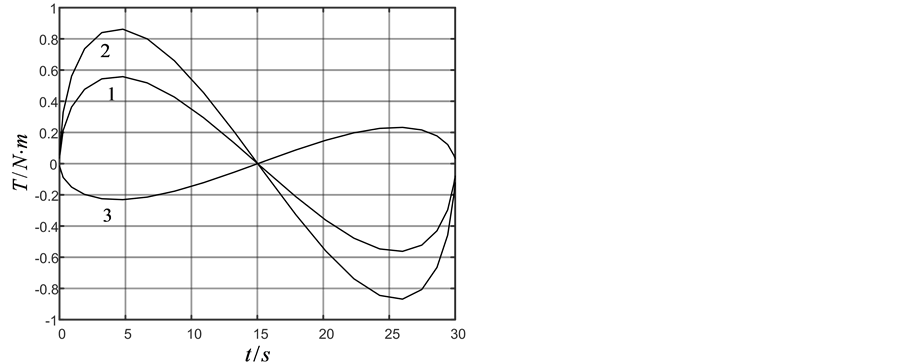
同样为与近似动态规划方法作对比,采用遗传算法,分别采用20个时间步,步长1.5 s,仿真结果如图2(a)~(c)中虚线所示。采用近似动态规划方法,设迭代ADP算法的误差界为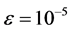 ,在时间
,在时间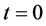 时
时

 (a) (b)
(a) (b)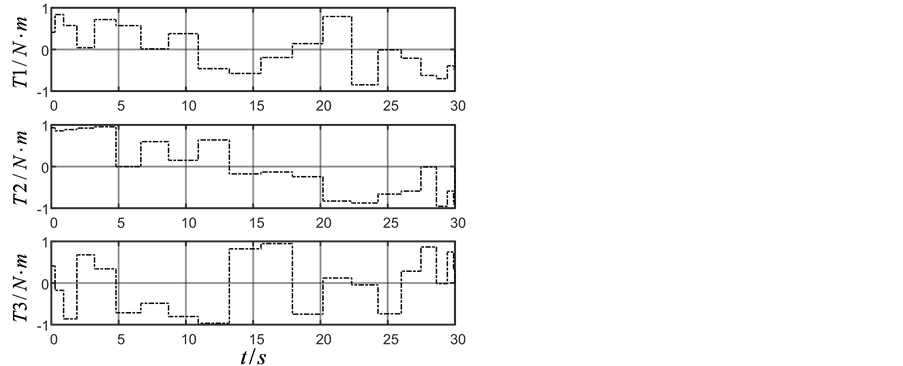
 (c) (d)
(c) (d)
Figure 2. (a) Attitude angle; (b) Angle velocity; (c) Control torque calculated by GA; (d) Control torque calculated by ADHDP
图2. (a) 姿态角度;(b) 角速度;(c) GA方法控制力矩;(d) ADHDP方法控制力矩
开始执行该算法,我们选择三层前馈神经网络作为执行网络与评价网络,其结构分别为6-12-3,9-12-1,两个神经网络的权值随机初始化在[−1,1]之间,训练评价网络与执行网络20次迭代,每次迭代1000个训练步,确保达到给定误差界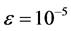 ,在训练过程中
,在训练过程中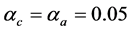 ,迭代ADHDP算法仿真结果如图2(a),图2(b),图2(d)中实线所示。在图2中标注1、2、3分别对应三轴卫星的三个轴。由GA和ADHDP的对比可知,由于GA是基于随机搜索的方法寻找能够实现一定目标的控制策略的,因此其控制力矩显得杂乱无章,而ADHDP方法,是先通过在线学习再去优化控制,所以其控制力矩曲线较为光滑。
,迭代ADHDP算法仿真结果如图2(a),图2(b),图2(d)中实线所示。在图2中标注1、2、3分别对应三轴卫星的三个轴。由GA和ADHDP的对比可知,由于GA是基于随机搜索的方法寻找能够实现一定目标的控制策略的,因此其控制力矩显得杂乱无章,而ADHDP方法,是先通过在线学习再去优化控制,所以其控制力矩曲线较为光滑。
5. 结论
本文采用了ADHDP和GA算法两种智能优化算法对三轴卫星姿态单轴机动和三轴机动路径规划控制做了比较,从仿真结果可以看出,近似动态规划的方法可以求解三轴卫星姿态机动的路径规划问题,并能求得较优的结果。三轴卫星是一个复杂非线性系统,对其进行姿态机动的能量最优控制问题的求解十分困难,本文提出了一种求解该问题的非线性控制方法,ADHDP方法采取非线性函数拟合方法逼近动态规划性能指标函数和最优控制律,通过它可以有效求解该类复杂非线性系统最优控制问题。
基金项目
中国国家自然科学基金(No.11472058)。
文章引用
王明泽,戈新生. 基于近似动态规划的三轴卫星姿态最优控制
Optimal Attitude Control of Three-Axis Satellite Based on Approximate Dynamic Programming[J]. 国际航空航天科学, 2017, 05(01): 27-36. http://dx.doi.org/10.12677/JAST.2017.51004
参考文献 (References)
- 1. 张化光, 张欣, 罗艳红, 等. 自适应动态规划综述[J]. 自动化学报, 2013, 39(4): 303-311.
- 2. 林小峰, 张衡, 宋绍剑, 等. 非线性离散时间系统带ε误差限的自适应动态规划[J]. 控制与决策, 2011, 26(10): 1586-1590.
- 3. Al-Tamimi, A., Vrabie, D., Abu-Khalaf, M., et al. (2007) Model-Free Approximate Dynamic Programming Schemes for Linear Systems. International Joint Conference on Neural Networks, Orlando, 12-17 August 2007, 371-378.
- 4. Jiang, Y. and Jiang, Z.P. (2013) Global Adaptive Dynamic Programming for Continuous-Time Nonlinear Systems. IEEE Transactions on Automatic Control, 19, 1-13.
- 5. Lee, J.Y., Jin, B.P. and Choi, Y.H. (2009) Model-Free Approximate Dynamic Programming for Continuous-Time Linear Systems. IEEE Conference on Decision and Control, Shanghai, 15-18 December 2009, 5009-5014.
- 6. Tang, K.W. and Srikant, G. (1997) Reinforcement Control via Action Dependent Heuristic Dynamic Programming. International Conference on Neural Networks, Vol. 3, Houston, 12 June 1997, 1766-1770.
- 7. Murray, J.J., Cox, C.J., Lendaris, G. G., et al. (2002) Adaptive Dynamic Programming. IEEE Transactions on Systems Man & Cybernetics Part C Applications & Reviews, 32, 140-153. https://doi.org/10.1109/TSMCC.2002.801727
- 8. Ding, W., Liu, D. and Wei, Q. (2011) Adaptive Dynamic Programming for Finite-Horizon Optimal Tracking Control of a Class of Nonlinear Systems. 30th Chinese Control Conference, Yantai, 22-24 July 2011, 2450-2455.
- 9. Liu, D., Wang, D. and Yang, X. (2013) An Iterative Adaptive Dynamic Programming Algorithm for Optimal Control of Unknown Discrete-Time Nonlinear Systems with Constrained Inputs. Information Sciences, 220, 331-342. https://doi.org/10.1016/j.ins.2012.07.006
- 10. Liu, D. (2005) Approximate Dynamic Programming for Self-Learning Control. Automatica, 31, 13-18.
- 11. Jiang, Y. and Jiang, Z.P. (2012) Computational Adaptive Optimal Control for Continuous-Time Linear Systems with Completely Unknown Dynamics. Automatica, 48, 2699-2704. https://doi.org/10.1016/j.automatica.2012.06.096
- 12. Wang, D. and Liu, D. (2013) Neuro-Optimal Control for a Class of Unknown Nonlinear Dynamic Systems Using SN-DHP Technique. Neurocomputing, 121, 218-225. https://doi.org/10.1016/j.neucom.2013.04.006
- 13. Zhu, Y., Zhao, D. and Liu, D. (2015) Convergence Analysis and Application of Fuzzy-HDP for Nonlinear Discrete-Time HJB Systems. Neurocomputing, 149, 124-131. https://doi.org/10.1016/j.neucom.2013.11.055
- 14. Si, J. and Wang, Y.T. (2000) On-Line Learning Control by Association and Reinforcement. IEEE Transactions on Neural Networks, 12, 264-276. https://doi.org/10.1109/72.914523
- 15. Wei, Q., Song, R. and Sun, Q. (2015) Nonlinear Neuro-Optimal Tracking Control via Stable Iterative Q-Learning Algorithm. Neurocomputing, 168, 520-528. https://doi.org/10.1016/j.neucom.2015.05.075
- 16. 章仁为. 卫星轨道姿态动力学与控制[M]. 北京: 北京航空航天大学出版社, 1998.
- 17. 黄静. 三轴稳定航天器姿态最优控制方法研究[D]: [硕士学位论文]. 哈尔滨: 哈尔滨工业大学, 2010.
- 18. 郭金良. 三轴稳定卫星姿态机动的时间最优控制[D]: [硕士学位论文]. 哈尔滨: 哈尔滨工业大学, 2013.
- 19. 安晓风. 卫星相对姿态智能自适应控制及分布式仿真技术研究[D]: [硕士学位论文]. 北京: 北京理工大学, 2016.
