 Smart Grid 智能电网, 2011, 1, 68-72 http://dx.doi.org/10.12677/sg.2011.13014 Published Online December 2011 (http://www.hanspub.org/journal/sg) Copyright © 2011 Hanspub SG Pareto Multi-Objective Distribution Network Reconfiguration Based on Improved Niche Particle Swarm Optimization Algorithm Hongli Sun, Zhengang Zhang Handan Power Supply Company, Handan Email: zhangzhengangwf@126.com Received: Sep. 28th, 2011; revised: Nov. 14th, 2011; accepted: Nov. 18th, 2011. Abstract: Distribution networ k reconfiguration can improve th e operation security, economy and power qua- lity of distribution network, for the current national construction and application of distribution automation system it has great significance. This paper presents a multi-objective distribution network optimal reconfi- guration of the particle swarm algorithm which based on a niche technology, the introduction of the concept of Pareto optimal to achieve a true sense of the multi-objective optimization; ap ply the particle swarm algori- thm to achieve the search of the Pareto optimal solution set of multi-objective reconfiguration, using niche technology and mutation operators to maintain the population diversity and dispersion, improved particle swarm algorithm global convergence reliability and convergence speed. Theoretical analysis and numerical results show that: distribution network reconfiguration based on niche particle swarm optimization meet the requirements in the speed and accuracy, and have more practical significance than the single-objective op- timization. Keywords: Distribution Network Reconfiguration; Pareto; PSO; Niche 基于小生境粒子群算法的 Pareto 多目标配电网重构 孙红丽,张振刚 邯郸供电公司,邯郸 Email: zhangzhengangwf@126.com 收稿日期:2011 年9月28 日;修回日期:2011 年11 月14 日;录用日期:2011 年11 月18 日 摘 要:配电网重构可以提高配电网运行的安全性、经济性和供电质量,对于当前国内配电自动化系 统建设和应用具有重要意义。笔者在《电力系统保护与控制》第 5期通过“基于改进小生境遗传算法 的Pareto 多目标配电网重构”中所运用的方法进行了优化尝试,达到了优化的效果。但为了从不同方 法实现优化效果,该文又提出一种基于小生境技术的多目标配电网最优重构的粒子群算法,引入 Pareto 最优的概念,实现了真正意义上的多目标优化;用粒子群算法实现对多目标重构问题的Pareto 最优解 集的搜索,采用小生境技术和变异操作保持种群的多样性和分散性,改善了粒子群算法的全局收敛可 靠性和收敛速度。理论分析和算例结果表明:基于小生境粒子群算法的配电网重构在速度上和精度上 能满足要求,并且较单目标优化更具工程实际意义。 关键词:配电网重构;Pareto;粒子群算法;小生境 1. 引言 配电网络重构是优化配电系统运行的重要手段, 是配网自动化研究的重要内容,在正常运行条件下, 配电调度员根据运行情况进行开关操作以调整网络结 构,一方面平衡负荷[1,2],消除过载,提高供电质量; 另一方面降低网损[3],提高系统的经济性。对于配电  孙红丽 等 基于小生境粒子群算法的 多目标配电网重构69 Pareto 网的重构问题,国内外学者提出了诸如模拟退火算法、 遗传算法、禁忌搜索算法等来解决[4-8]。但是,大部分 的解决方法都是以单目标或多目标加权成单目标的形 式进行分析。单一目标不能完整的反映实际配电网重 构的要求,而加权的方法则更加依赖于人的经验。网 络重构问题本身要求算法能快速给出结果,而针对多 目标优化问题的算法在计算速度上都有不足。本文针 对以上配电网重构中存在的问题提出了基于小生境粒 子群算法的 Pareto 多目标配电网重构,将系统有功网 损,节点最低电压幅值、操作开关次数作为目标,运 用小生境粒子群算法搜寻 Pareto 最优解。种群多样性 的保持由变异操作完成,而小生境技术保持了种群的 分散性,这都使粒子向 Pareto 最优解靠近。实际中决 策者可以结合具体的情况,选出适宜的重构方案。这 比单一目标或者加权多目标得出的单个最优解有更好 的实用性和合理性。 2. 多目标配电网重构的数学模型 2.1. 配电网拓扑结构的简化[9] 将配电网络看作是一种赋权图,将线路上的柱上 开关看作是节点,节点的权为流过该节点的负荷。将 相邻的两个节点间的配电馈线和配电变压器综合看作 是图的边,边的权即是该条边上所有配电变压器供出 的负荷之和。这样处理之后达到了简化节点数的目的, 从而构成了配电网的数学模型。 2.2. 多目标配电网重构的数学模型 2.2.1. 目标函数 配电系统有功损耗表达式[9]: 22 2 1 Minimize b NN ii iiii i LRPQU RI 2 1 b i (1) 式中,表示网络中的支路总数; 和表示 流过支路 的有功功率和无功功率; 表示支路 的 支路电阻;表示支路 的末端电压。 b N i U i Pi Q i bi Ri b i b 在降低网络有功损耗的同时,系统电能质量也是 现代电力系统较为关注的一个方面。配电网中各节点 电压偏离标准电压幅值的大小,一定程度上反映了配 电网系统的电能质量。由于配电网在运行时呈辐射状, 使得配电网中各节点电压从电源点向末梢点逐次降 低,因此监测配电网中电压最低点的幅值大小同样能 够达到与上式相同目的。此时目标函数为[10]: Maximize :min, n VnNR (2) 其中 表示节点电压, n V R N表示网络中节点总数。 网络重构的最终方案由一些开关操作构成,开关 闭合和断开都会对开关的寿命产生影响。从延长开关 寿命方面考虑,结合操作安全性因素,以及进行操作 所需的人力和时间,应该尽量减少对开关的频繁操作, 使开关操作的次数尽可能少。目标函数可表示为[11]: Minimize :op n (3) 其中 表示开关操作次数。 op n 2.2.2. 约束条件 约束条件为: 1) 电压幅值:min maxi VVV; , R ii N 2) 电流偏移: ,maxjj II; ,b jj N 3) 供电约束:配电网必须满足负荷的要求,而且 不能有孤立节点(即“孤岛”)。 4) 网络拓扑约束:配电网一般为闭环设计、开环 运行,这就要求重构后的配电网必须为辐射状。 其中, i V是母线 i上的电压, 和分别是 母线电压的最大值和最小值; min Vmax V j I 是支路 电流幅值, 是支路上 允许通过的电流最大值;和 j b N ,maxj I j R N分 别是支路和节点集合。 3. 多目标优化的小生境粒子群算法 3.1. 基本粒子群算法 粒子群优化算法是一种新的进化计算技术,源于 对鸟群捕食行为的研究。在 PSO 系统中,每一个备选 解被称为一个“粒子”,多个粒子共存、合作寻优, 每个粒子根据自身的“经验”在问题空间中向最好的 位置飞行,搜索最优解。 PSO 的数学表示如下: 设搜索空间为D维,总粒子数为N,第 个粒子 的空间位置为 i 12 ,,, iii iD X xx x;第个粒子飞行历 史中的最优位置为 i iD12 ,, iii Ppp,p,设 g P为所有 中的最优值;第 个粒子的速度为向量 i P i 3 , i v 12 ,, iii vvV;每个粒子的位置按如下公式进行 变化: Copyright © 2011 Hanspub SG  孙红丽 等 基于小生境粒子群算法的 多目标配电网重构 Pareto 70 1 2 1 ididid id gd id vtvt crandPtxt crandP tx t (4) 11 idid id xtxt vt (5) 其中, 、是正常数,称为加速因子; 1 c2 c rand 为0到1之间的随机数; 称为惯性因子。粒子群初 始位置和速度随机产生,然后按式(4)、(5)进行迭代, 直到找到满意解。 3.2. 多目标小生境粒子群算法 在可行解空间中均匀随机初始化粒子群,选取其 中非劣解粒子,作为“精英集”;通过小生境技术给 精英集中的非劣解粒子分配适应度值,聚集程度越大 的粒子适应度越小,精英集中第 个粒子的适应度为: i 1 , jP Fi s dij (6) , 1, , 0, dij dij sdij dij (7) 其中 ,dij为第 个粒子和第个粒子的距离,i j 为小生境半径。 采用与适应度值成正比的轮盘赌方法选取精英集 中的个体作为粒子群体历史最佳 g P;按照式(4)、(5) 进行迭代,选出粒子群中非劣解,加入精英集,并删 除其中的劣解,形成新的精英集;若精英集超出容量, 则删除其中部分适应度小的个体;迭代多次后的精英 集就是算法所得的非劣解集。 4. Pareto最优解的概念 在进行多目标重构时,使各个目标函数同时达到 最优的情况很难出现,于是解决多目标重构问题的最 终手段就是在目标函数之间进行协调和折中,使目标 函数尽可能的达到最优,因而出现了基于权重系数多 目标算法。如前所述,这种多目标算法对经验知识的 要求比较高。另外,不同目标的单位也不一样,不易 直接比较。同时,各目标之间通过决策变量相互制约, 往往存在相互矛盾的指标。为此,本文采用 Pareto 最 对于两个决策变量 u和v,且 u 优的概念来解决多目标重构问题。 , 为决策 变量 ,v SS 空间,对任意的 1, 2,ik , ii f ufv,并 且存在 1, 2,ik ,使得 ii f ufv 成立,则称决 策变量 u为u 对于多目标优化问 一个 支配 v,记v。 x S题的 可行解,当且仅 当S中不存在y,使 yx,即 x 是S中的非支配个体, 称 x 为多目标优化 题的to 最优解。所谓 Pareto 最优解就是不存在比这个方案至少一个目标更好而其 他目标不低劣的更好的解,也就是不可能优化其中部 分目标而使其他目标不劣化。 对于 Pareto 最优解来说,它会形成 Paret 问Par o最优解 点组 优化问题的 Pareto 最优解是一个集。 对于 5.1 操作 的选取 每次迭代后产生的新种群中可能会存在更优的非 e即 成的线。 通常多目标 实际应用问题的最后方案决策,必须根据对问题 的了解程度和决策人员的偏好,从多目标优化问题的 Pareto 最优解集里面挑选出一个或部分解作为所求多 目标优化问题的最优解[12]。因此求解多目标问题的首 要步骤和关键是求出尽可能多的 Pareto 最优解。 5. 基于小生境粒子群算法的多目标 配电网重构 . 编码 配电网重构问题的定义就是选择一组合适的开关 来实现重构,因此将开关进行编码简单又直观。 本文将可以操作的开关的状态作为粒子的位置,由于 其值只有 1和0,所以相应的粒子群算法采用二进制 粒子群算法。 5.2. 非支配解 Figure 1. Pareto front nominal and under parameter tolerances 图1 . Pareto最优解点组成的线 Copyright © 2011 Hanspub SG  孙红丽 等 基于小生境粒子群算法的 多目标配电网重构71 Pareto 支配解,非支配解的选择方式如下:对于一个粒子, 粒子(全局历史最优)决定了 粒子 的计算 ,需要首先计算精英集中各个 非支 将它与种群中的其他粒子两两比较Pareto 优胜关系, 如果它不劣于其它粒子以及精英集中的粒子,那就把 它加入精英集中。最后删除精英集中的劣解。 5.3. 领导粒子的选择 粒子群算法中的领导 的前进方向,本文的问题由于有多个目标,因而 粒子的最终“目的地”不是只有一个。为了保持种群 的分散性(有利于找到更多 Pareto 可行解),领导粒子 的选取不能只针对一个目标,因而采用从精英集中根 据适应度的大小按轮盘赌的方法随机选取粒子作为领 导粒子。 5.4. 适应度 为了选取领导粒子 配解的适应度。本文采用小生境技术给各个非支 配解分配适应度。各非支配解的适应度按式(6)、(7) 计算。由于采用二进制编码,其中粒子间的距离 ,dij 采用下式计算: ,im jm mD dijbb (8) 式中:D为粒子群编码串位数, j m b为第 个粒子 第 i m位的值, j m b为第 j个粒子第 m位 值。 5.5 粒子的更 的 . 新 群的特殊性,粒子的更新不同于 普通 多样性,本文将遗传算法中的变 异操 子变异两个环节后有可能产 生不 进化代数 由于二进制粒子 粒子群算法。本文采用文献[7]提出的粒子更新方 法来更新粒子的速度和位置。 5.6. 粒子的变异 为了保持种群的 作引入粒子群算法。对于劣于其个体历史最优 i P 的粒子,以变异率 P对粒子的各位进行变异。 5.7. 不可行解的修复 由于在粒子更新和粒 满足配电网辐射状结构的不可行解,所以要对包 含环路和孤岛的粒子进行修复。 6. 算法的具体实现步骤 ,精英集 容量 机产生 N个粒子,然后调用修复程序修复其 中的 数。 精英集并计算各 个非 选取历史最佳即领导粒子,然 后更 入精英集并删除其 中的 最 佳; V。 2) 随 1) 确定种群规模N,种群 g N 不可行解,从而生成初始种群。其初始位置作为 每个粒子个体历史最优 i P。 3) 计算所有粒子的目标函 4) 筛选粒子群中的非劣解加入 劣解的适应度。 5) 根据适应度大小 新粒子的速度和位置。 6) 计算粒子的目标函数。 7) 选取粒子群中的非劣解加 劣解,然后计算所有非劣解的适应度。若精英集 中的个体数超出其最大容量,则按超出容量数的二倍 选取适应度最小的个体,随机删除其中的 50%。 8) 若当前粒子由于其历史最佳,则替换其历史 若不劣于其历史最佳,则按 50%的概率替换其历 史最佳;若当前粒子劣于其历史最佳,则保留其历史 最佳,并对粒子进行变异操作。 9) 如果迭代次数到达 g N,输出结果;否则,跳 转到 分析 有32 条线路,5条联 络开 算,选 取种 度快。所以以 粒子 了一 步骤(5)。 7. 算例结果与 IEEE 33节点[13]配电网络具 关支路,基准电压为 12.66 kV,整个网络总负荷 为5084.26 kVA + j2547.32 kVA。所有的程序在 Matlab 平台上仿真运行。该网络结构如图2所示。 应用小生境粒子群算法对算例进行仿真计 群规模为100,种群进化代数为20,精英集容量 为10。运行本文的小生境粒子群算法,在 1~2 秒可以 得出 Pateto 最优解集,如表 1所示。 粒子群算法简单易于实现,收敛速 群算法为基础的多目标小生境粒子群算法在计算 速度上比其他算法有很大优势。从该仿真算例的结果 来看,运用本章的方法得到了一组重构结果,为决策 者提供了更多的选择方案。决策者可以结合实际的情 况,在其中选出适宜的重构方案。 8. 结论 配电网络重构是一个多目标优化问题。本文提出 种Pareto最优与小生境技术相结合的粒子群算法 进行多目标配电网络的重构。该算法不仅是单目标配 Copyright © 2011 Hanspub SG 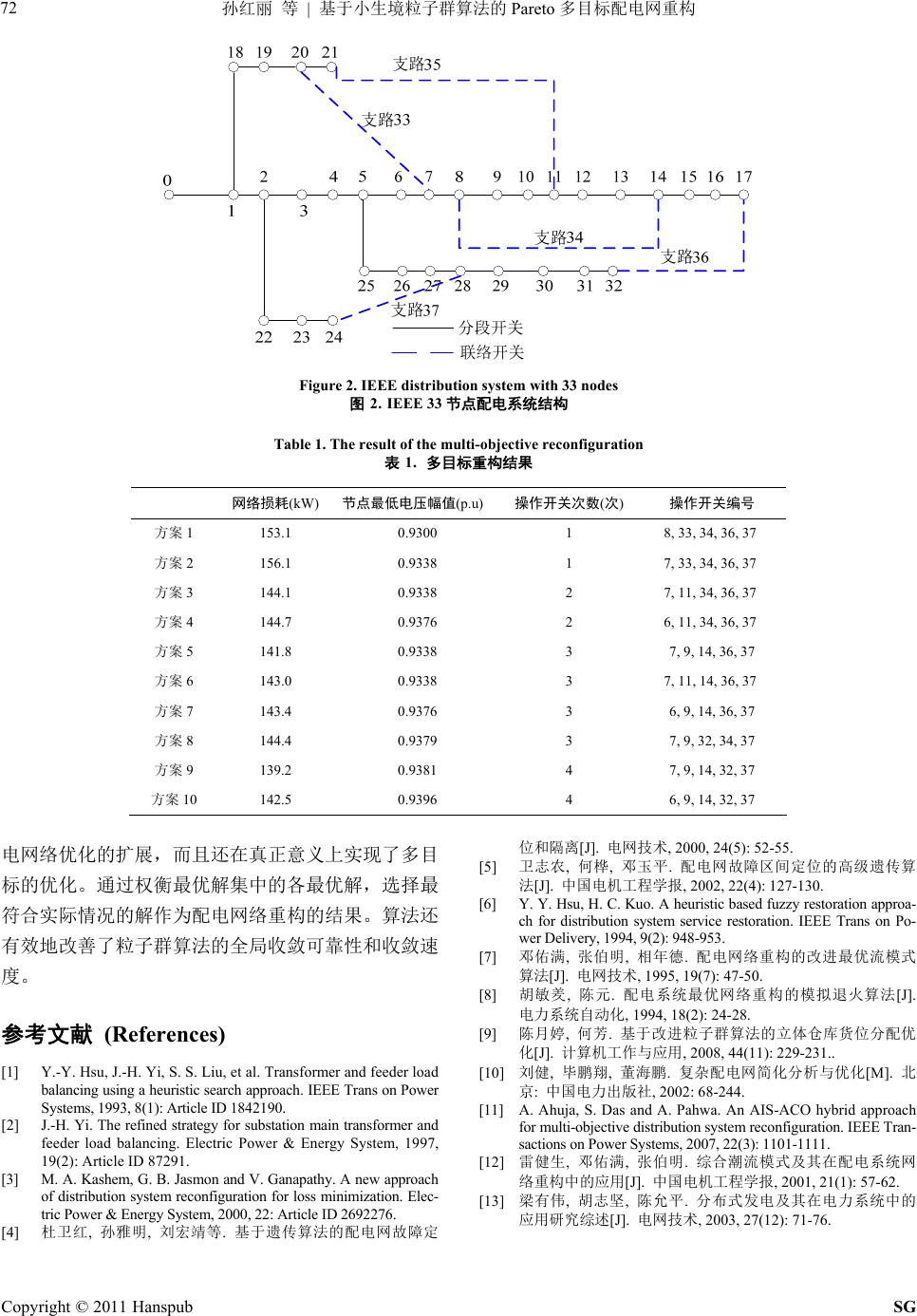 孙红丽 等 基于小生境粒子群算法的 Pareto 多目标配电网重构 Copyright © 2011 Hanspub SG 72 Figure 2. IEEE distribution system with 33 nodes Table 1. The ration 网络损耗(kW) 节点最低电压幅值 (次)操作开关编号 图2. IEEE 33节点配电系统结构 esult of the mi-objective reconfigurult 表1. 多目标重构结果 (p.u) 操作开关次数 方案 1 153.1 0.9300 1 8, 33, 34, 36, 37 方案 2 156.1 0.9338 1 7, 33, 34, 36, 37 方案 3 144.1 0.9338 2 7, 11, 34, 36, 37 方案 4 144.7 0.9376 2 6, 11, 34, 36, 37 方案 5 141.8 0.9338 3 7, 9, 14, 36, 37 方案 6 143.0 0.9338 3 7, 11, 14, 36, 37 方案 7 143.4 0.9376 3 6, 9, 14, 36, 37 方案 8 144.4 0.9379 3 7, 9, 32, 34, 37 方案 9 139.2 0.9381 4 7, 9, 14, 32, 37 方案 10 142.5 0.9396 4 6, 9, 14, 32, 37 电网络优化的扩展,而且还在真正意义上实现了多目 参考文献 (References) al. Transformer and feeder load 位和隔离[J]. 电网技术, 2000, 24(5): 52-55. : 1101-1111. [5] 卫志农, 何桦, 邓玉平. 配电网故障区间定位的高级遗传算 法[J]. 中国电机工程学报, 2002, 22(4): 127-130. Y. Y. Hsu, H. C. Kuo. A heuristic based fuzzy 标的优化。通过权衡最优解集中的各最优解,选择最 符合实际情况的解作为配电网络重构的结果。算法还 有效地改善了粒子群算法的全局收敛可靠性和收敛速 度。 [6] restoration approa- ch for distribution system service restoration. IEEE Trans on Po- wer Delivery, 1994, 9(2): 948-953. [7] 邓佑满, 张伯明, 相年德. 配电网络重构的改进最优流模式 算法[J]. 电网技术, 1995, 19(7): 47-50. 胡敏羑 陈元. 电系统 优网[8] , 配最 络重构的模拟退火算法[J]. 电力系统自动化, 1994, 18(2): 24-28. 陈月婷, 何芳. 基于改进粒子群算法的[9] 立体仓库货位分配优 化[J]. 计算机工作与应用, 2008, 44(11): 229-231.. ] 刘健, 毕鹏翔, 董海鹏. 复杂配电网简 [1] Y.-Y. Hsu, J.-H. Yi, S. S. Liu, et[10 化分析与优化[M]. 北 京: 中国电力出版社, 2002: 68-244. A. Ahuja, S. Das and A. Pahwa. An AIS-ACO hybr balancing using a h euristic search approach. IEEE Trans on Power Systems, 1993, 8(1): Article ID 1842190. [2] J.-H. Yi. The refined strategy for substation main transformer and feeder load balancing. Electric Power & [11] id approach for multi-objective distribution system reconfiguration. IEEE Tran- sactions on Power Systems, 2007, 22(3) Energy System, 1997, 19(2): Article ID 87291. [3] M. A. Kashem, G. B. Jasmon and V. Ganapathy. A new approach of distribution system reco [12] 雷健生, 邓佑满, 张伯明. 综合潮流模式及其在配电系统网 络重构中的应用[J]. 中国电机工程学报, 2001, 21(1): 57-62. 梁有伟, 胡志坚, 陈允平. 分布式发电及其在电 nfiguration for loss minimization. Elec- tric Power & Energy System, 2000, 22: Article ID 2692276. [4] 杜卫红, 孙雅明, 刘宏靖等. 基于遗传算法的配电网故障定 [13] 力系统中的 应用研究综述[J]. 电网技术, 2003, 27(12): 71-76. |