 Hans Journal of Computational Biology 计算生物学, 2011, 1, 22-26 http://dx.doi.org/10.12677/hjcb.2011.12004 Published Online December 2011 (http://www.hanspub.org/journal/hjcb) Copyright © 2011 Hanspub HJCB Likelihood Ratio-Permutation Test of Differentially Expressed Cancer-Related Genes Jingzhe Li, Guofen Zhang Department of Mathematics, Zhejiang University, Hangzhou Email: zhang-hh@zju.edu.cn Received: Sep. 18th, 2011; revised: Oct. 23rd, 2011; accepted: Oct. 25th, 2011. Abstract: The particularity of the differentially expressed cancer-related genes brings new challenges in the field of gene selection. Statisticians have succeeded in proposing new statistics and methods to solve the problem of selecting differentially expressed cancer gene. This article will advance a new method called “Likelihood Ratio-Permutation Test”, in order to select differentially expressed genes under the cancer model, after referencing some existing research. Keywords: DNA Microarray (Gene Chips); Gene Selection; Likelihood Ratio Test; Permutation Test 癌症差异表达基因的似然比–置换检验法 李靖喆,张帼奋 浙江大学数学系,杭州 Email: zhang-hh@zju.edu.cn 收稿日期:2011 年9月18 日;修回日期:2011 年10月23 日;录用日期:2011 年10 月25 日 摘 要:癌症的差异表达基因具有其特殊性,这种特殊性给基因选择带来了新的挑战。许多统计学家 提出了新的统计量和检验方法,不断地在这一领域取得突破和完善。本文将在借鉴这些已有研究成果 的基础上,运用统计学中两种经典的常用方法,提出一种有效的手段——似然比–置换检验法,用以 甄选癌症的差异表达基因。 关键词:DNA 微阵列(基因芯片);基因选择;似然比检验;置换检验 1. 引言 差异表达基因的检测问题一直以来在生物科学领 域中占据着重要的地位。近年来,DNA 微阵列技术 (microarray)——又称为基因芯片(gene chip)取得了令 人瞩目的发展。这项技术可以在同一时间对大量基因 表达水平精确、快速的分析并予以记录,多以矩阵形 式表示。其中n代表样本容量,p为基因数量, 通常有 [1]。 ij np x pn 鉴于此,人们往往需要从成千上万个基因中筛选 出与某一特定疾病相关的基因,从而通过控制这些致 病基因,以达到控制疾病的目的[2]。那些在患病者的 样本和正常人样本上表达有显著差异的基因,很自然 的被认为同这一疾病有着明显的关系,即为致病基因。 传统的单个基因两样本 t检验被广泛地运用于差 异表达基因的检验。然而,Tomlins 等人在对前列腺 癌症(Prostate Cancer)的差异基因表达的研究中发现 t 检验并没有取得所预期的效果[3]。于是,他们在对基 因芯片进行细致分析之后指出,致病基因并非在所有 实验组样本中,而仅仅是在其一个子集上都显示出差 异表达的特性。而在此模型下,实验组与对照组的样 本均值的差异往往不那么明显。 D. Ghosh等人在 2008 年提出了上述差异表达的 概率分布模型[4]。他们假设致病基因在对照组全体和 实验组的一个子集上服从同一分布 0 F ,而在实验组的 其他样本上服从另一分布 1 F ,即: 12 0 ,,, ~ m x xxF  李靖喆 癌症差异表达基因的似然比–置换检验法 23 1200 0 ,,, ~π1π n y yy FF (1) 其中 ,且 0 0π1 0 F F 令,我们可以考虑对于某个k, 来自于不同的分布,1。其 中 的 ,即实验组数据中那些差异表达的部 分, 通常被称作异常值(outlier)。2005 年Tomlins 等人 提出的 COPA 统计量[3],R. Tibshirani等在 2007 年提 出的 OS 统计量[5]以及H. Lian等在 2008年提出的 MOST 统计量[6]都在一定程度上改进了 t统计量的不 足,并取得了良好的效果。 12 n yy y 12 ,,, n y 12 ,,, n y kk yy kk yy kn 然而,上述方法仍然面临着一些共同的缺陷。其 中重要的一点是,上述方法所用到的统计量大都是基 于分位数来建立的,而分位数的选择具有相当大的主 观性。鉴于我们事先往往并不知道异常值的个数或所 占的比例,故很难用一个普遍的标准去代表所有的模 型。此外,鉴于分位数和中位数的分布难以获得,这样 的方法也不能提供有效的论证来阐明其检验水平 。 本文中,我们将基于第一部分所述的模型,给出 一种以似然比检验为基础的差异基因判别法。 2. 方法 似然比检验是统计学中的一个经典而常见的方 法。它常用于区分某一批样本是来源于两个已知分布 中的哪一个[7]。 本文最终的目的是要对于单个基因 g,做如下检验: 0 1 : : Hg Hg 基因 非致病基因 基因是致病基因 (2) 设基因 g在m个对照组样本和 n个实验组样本上 的基因表达水平分别为 12 ,, , m x xx和 。 假设差异表达部分要普遍高于正常值,我们记: 12 ,,, n yy y 1212 1 ,,,,,, ,,, mnm n zzzxxxyy . 于是,上述 1 H 成立,当且仅当 12 ,, , m x xx和 服从(1)中的分布;而 12 ,,, n yy y0 H 成立则等价于 。亦即我们只需检验: 12 ,,..., mn zz z 0 ~F 012 0 112 012 000 1001 :,, ,~ :,,,~,, ,, ~π1π,0 π1, . mn mn Hzz zF H xxx Fyyy F FF F (3) 至此,检验问题转化为样本 12 ,,, mn zz z 来自于 哪一个分布的问题。为简单起见,我们进一步假设 0 F 和1 F 均为正态分布,且方差相等。即: 22 0011 ~,,~,FN FN 这样,上述假设检验问题可继续转化为: 2 12 0 ,,, ~,, m xxx N 0 00 , ~π,1π n y N 0 0π1. 22 12 1 ,, ,,yy N ::HH 00 110 1 . 接着,构造如下似然比统计量: 0 0 1 1 sup sup mn i i mn i i f z f z (5) 其中,待估参数 01 0 ,,,π ; 为全 参数空间, 01 0 | 0 为 H 成立时的子参数空 间, 0 , ii f zfz 1, 2 分别为参数空间 ,下的概 率密度函数, 0 i z , ,imn 。 当 时,有如下的: 2 0 2 2 0 02 2 1 02 1exp,1, , 2 2π 1 πexp 2 2π 1 (1 π)exp , 2 2π 1, , i i i i zim z fz z im mn (6) 对(6)式中的各待估参数 01 ,,,π0 分别求其极 大似然估计(MLE),代入上式即可得到 时的极大 似然函数值。但是这些极大似然估计难以得到显式表 达,因此接下来需要对其作出一个近似的估计。 这里不妨用异常值(outlier) 个数的估计来代替对 的估计。这时,令 0 π12 n yyy ,当其中异常值 的个数为 nk 时,有: 2 0 2 2 1 2 1exp , 2 2π 1, , 1exp , 2 2π 1, , i ii z imk fz z imk mn (7) Copyright © 2011 Hanspub HJCB  李靖喆 癌症差异表达基因的似然比–置换检验法 24 其中, 。进而对于新的待估参数 11kn ,,,k ,有: * 01 *2 11 2 1 2 1 sup supexp ˆ 2 ˆ 2π ˆ 1exp ˆ 2 ˆ π mn mki ik ii mn i i z fz z (8) 其中, 2 0 ˆ 12 mk ˆ , 01 ˆˆ , 分别为 01 ,, 在中的极大似 然估计。经过简单计算得: 01 11 22 2 01 11 2 11 ˆˆ 1 ˆˆ , 2 ˆˆ mk mn ii iimk mk mn ii iimk zz mk nk zz mn ˆ (9) 的范围内。这是便根据假设检验的原则拒绝原假设 0 H ,接受 1 H ,认为所检验的基因 g是致病基因。 首先,我们利用数学软件进行模拟实验。假设 m = n = 2,模拟 式的样本: 3. 模拟和实例 67 12 12 , ,, , xx yy xx 17 ,,yy 0下列 5种形 每组数据产生后,首先计算 1 2201220 12 20125 , ,, , ,~0,1 (b) ,,,,,,~0,1 ,,, ~ 2,1 xyyyN xxxyyyN yyyN 当* 0 ,即 01 时,有: 0 2 2 1exp , 2 2π 1, 2,, i i z fz imn (10) 这时易得: 0 0 *00 0 2 2 11 ˆ () 1 sup( )expˆ 2 ˆ 2π mn mni i ii z fz (11) 类似上面的推导,有: 0 00 1 2 2 1 2 1 ˆ 1 ˆˆ , 1 ˆˆ mn i i mn i i z mn z mn 将(7)~(12) 代入(5),可计算出似然比统计量 00 (12) 的 值。 接下来,我们对实验组和对照组的共 m + n个数 据重新排序,得到 的一组 ,采 算出相应的 12 ,,, mn zz z 用上节中的方法计 置换样本 12 ,,, mn zz z 1 。 进行N次,利用数学软件, 得出 这样的置换我们可以并将 的N个 值记作 12 ,,, N 。利用这些 12 ,,, N 给出在 0 H 成立时 在0 H 20 201 210 11 2012 1 (a) , , ,~0,1 , ~ 2,1 (e),,, , , yyy N y N xyy y 5 16 20 ~0,1 , ~ 4,1 N y N 12 (c) ,,,xxx 20 1 2201215 16 1720 (d) ,,,, , ,~0,1 ,,, ~ 2,1 xxxyyyN yyyN ,然后进行N = 1000 次置换,得出 1 21000 ,,, 。其中,大于 的值的个 M据各进行 100 ,得到 10 个M的 数统计 数记作 1 。以 100 ,M 上5组数 。表1给出这 次模拟 频 2 ,,MM0 M f 和频率 M p。 1中0 H 从表 我们可以看出:在实验(a)中,拒绝的 率约为 。对于非致病基因的检测结果合 表达基因 对= 异 为小 概 理的 于5 5% 。而 是比较 1 M 。在实验(b,c)中,当 01 ,1), (2,1)FN FN且异 常值的个数不少于一半 M的值在多数情况下小于 50,“似然比—置换检验法”较为有效地判别出差异 于实验(d)来说,当 F0 = N(0,1), F N(2,1)而 常值数目仅 (0 时, 5个时,只有约一半的 0。可是从相对于(d)拉大0 F 和1 F 均值之间差 方 差相对不变)的实验(e)来看,检验又基本恢复了有效 性。造成这一现象的原因 拟数 据的固有误差。这里 0 距( 模 可能有如下两点:1) F 和1 F 两个正态分布的均值,在 实验(a~d)中差别相对较小,而在(e)中相对较大;2)置 换检验本身的误差。当原先实验组数据 12 ,,, n y yy 中有 k个 12 ,,, nknkn y yy 属于异常值时,如果在 一次置换中这 k个数据的绝大 数 至全部恰好被分 配到实验组,这一次得出的新似然比 多 甚 j 会显著偏大. 当k = 5 时,异常值 16 1720 ,,, y yy均被分配到新的实 验组 12 ,,, n y yy 中的概率约为 2.4%,是一个不容忽 视的概率值。综合以上两个原因,便不难解释为何实验 (d)有超过一半的模拟造成了 50M的结果。 下的经验分布 函数,以模拟 在0 H 下的近似分布。对于给定的检验 水平 ,记 12 ,,, N 中大于 的值的个数为M。当 M N 时,表明 在该近似分布中位于上方 比例 Copyright © 2011 Hanspub HJCB 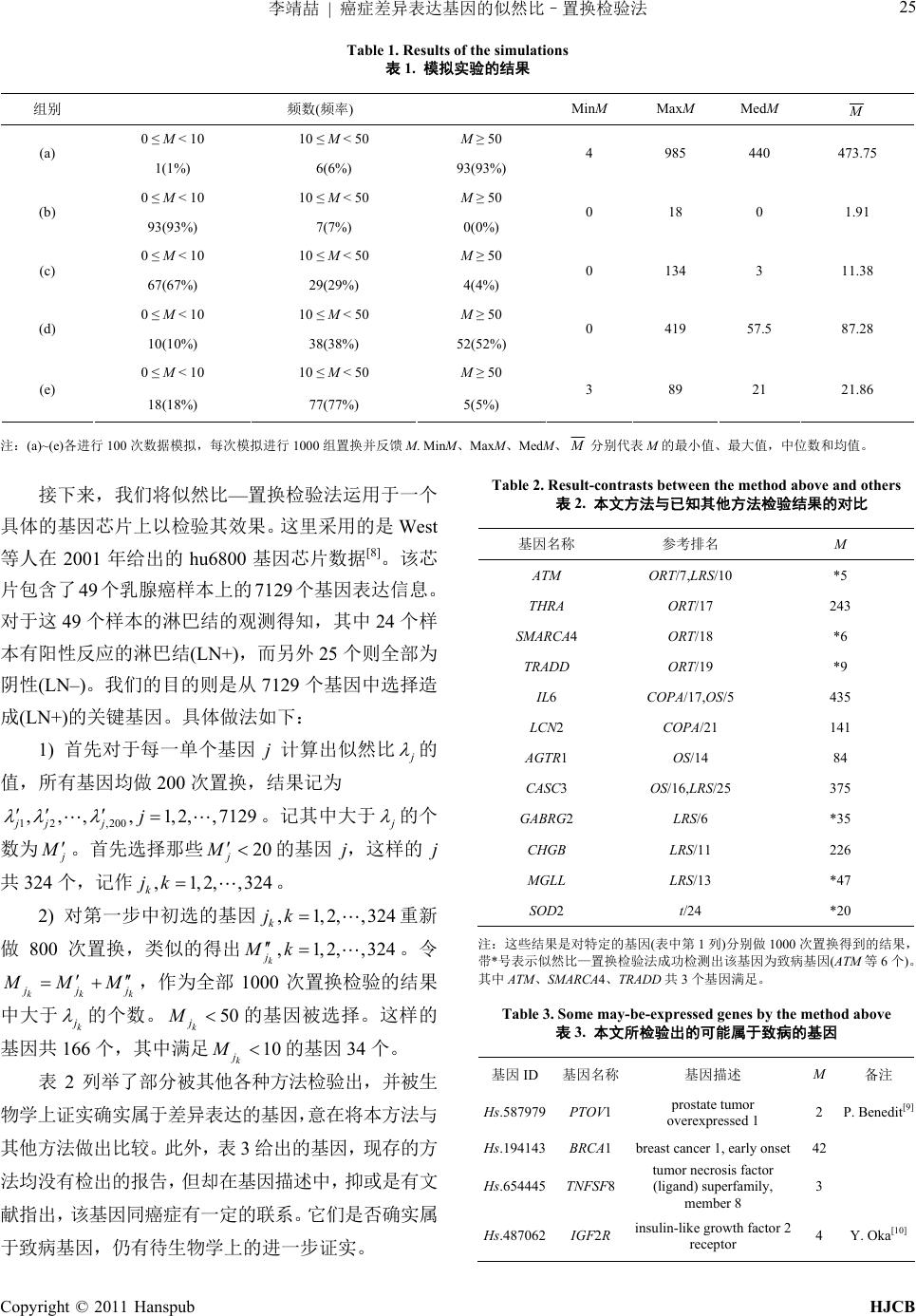 李靖喆 癌症差异表达基因的似然比–置换检验法 Copyright © 2011 Hanspub HJCB 25 s of tlations (频Med Table 1. Resulthe simu 表1. 模拟实验的结果 组别 频数 率) MinM MaxM M M 0 ≤ 10 ≤ M < 50 M < 10 M ≥ 50 (a) 1(1%) 6(6% 4 985 440 473.75 0 ≤ M < 10 10 ≤ M < 50 (b) 93(93%) 0(0%) 0 18 0 1.91 6 2 3 5 ) 93(93%) M ≥ 50 7(7%) 0 ≤ M < 10 10 ≤ M < 50 M ≥ 50 (c) 7(67%)9(29%)4(4%) 0 134 3 11.38 0 ≤ M < 10 10 ≤ M < 50 M ≥ 50 (d) 10(10%) 8(38%)52(52%) 0 419 7.5 87.28 0 ≤ M < 10 10 ≤ M < 50 M ≥ 50 (e) 18(18%) 77(77%) 5(5%) 3 89 21 21.86 M 注:(a 各进行 100 次数据每次模拟进行 100 馈M. MinM、 、MedM、)~(e) 模拟, 0组置换并反 MaxM分别代表 M中位数和均 —置换检验法运用于一个 具体的基因芯片上 其效果。这里是 West [8] 包含了 49 个乳腺癌样本上的7129 个基因表达信息。 对于 的最小值、最大值, 值。 接下来,我们将似然比 以检验 采用的 等人在 2001 年给出的hu6800 基因芯片数据 。该芯 片 这49 个样本的淋巴结的观测得知,其中 24个样 本有阳性反应的淋巴结(LN+),而另外 25 个则全部为 阴性(LN–)。我们的目的则是从 7129个基因中选择造 成(LN+)的关键基因。具体做法如下: 1) 首先对于每一单个基因j计算出似然比 j 的 值,所有基因均做 200次置换,结果记为 1 2,200 ,,,,1, 2,, 7129 jjj j 。记其中大于 j 的个 数为 j M 。首先选择那些 20 j M 的基 j j 。 2) 对第一步中初 4重新 做800 次置换,类似的得出 4 因 ,这样的 共324 个,记作 ,1,2,,324 k jk 选的基因 。令 kkk ,1,2,,32 k jk ,1,2,,32 k j Mk j jj M MM 中大于 ,作为全部 1000 次置换检验的结果 k j 的个数。 50M 足M k j k j 表列举 了部分 被其他各种方法检 其他方法 比较。给出的基因,现存的方 检出 抑或是有 的基因被选择。这 10的基因 34 个。 样的 ,其中满 2验出,并被生 物学上证实确实属于差异表达的基因 ,意在将本方法与 做出此外,表 3 法均没有 的报告,但却在基因描述中, 文 献指出, 于致病基因,仍有待生物学上的进一步证实。 ble 2. Result-contrasts between the method above a n d others 表2. 文方法与其他方 验结果的 基因名称 参考排名 M 基因共 166 个 Ta 本已知法检对比 ATM ORTLRS /7, /10 *5 THRA ORT/17 243 SMARCA4 ORT/18 *6 TRADD ORT/19 *9 IL6 COPA/17,OS/5 435 AGT O G LCN2 COPA/21 141 R1 OS/14 84 CASC3 S/16,LRS/25375 ABRG2LRS/6 *35 CHGB LRS/11 226 MGLL LRS/13 *47 SOD2 t/24 *20 注:这些 对特定的基因做1000 次置换得到的结果, 带*号表示似置换检验法成功因为致病基因等 6个)。 其中 AT 4、TRADD 满足。 Ta e may-be-expgenes by the method above 3. 本文所检于致病的基因 基因 名称述 M备注 结果是 然比— (表中第 1列)分别 检测出该基 (ATM M、SMARCA 共3个基因 ressed ble 3. Som 表验出的可能属 ID 基因 基因描 该基因同癌症有一定的联系。它 们是否确 实属 Hs.58797 PTOV1 9prostate tumor overexpressed 1 2 P. Benedit[9] Hs.19414 BRCA1 3breast cancer 1, early onset 42 Hs.654445TNFSF8 tumrosis factor or nec (ligand) superfamily, member 8 3 Hs.487062 IGF2R insulin-like growth factor 2 reptor 4 Y. Oka[10] ec  李靖喆 癌症差异表达基因的似然比–置换检验法 26 4. 在改进多法的基 上 虑两样本不同分布的角度入手,提出了用于癌症差异 表达基因判别的似然比 ,浅显易懂,操 作方便,并取得了良好的效果。似然比—置换检验法 方于,基于分 函 数考虑的似然比统计量更能有效和充分地代表数据本 身具有的特 失相对比较少。我们知 仅仅是利用中位数和上方 r分位 数(一般取 0.25)分别代表显著基因的属性。以模拟实 验(d~e)为例,上方 0.25分位数仍是从N(0, 1)中取 样本值,这使得差异表达部分的信息大量丢失。而基 于分布的统计量则有效的避免了这种信息丢失。对于 特定的临床试 根据需要确定检验水平。然 我们最终反馈 M并不是一个确定的结果而是 的,当异常值个数偏少的时候,检验错误的可能性 也将 量中用到了异常值部分的方 数为 1时本方法并不适用。 到的那些大于M的 结果与讨论 本文 借鉴和种现有方础,从考 —置换检验法 较COPA、ORT 等法具有的优势在布 征,信息损 道, COPA 、 ORT 等方法 到的 验,可以 的值 增加。由于似然比统计 估计,故当异常值的个 对于特定的基因来说,我们不知道置换反应所得 而, 随机 差的 j 的值, 少比例是因为 到底有多 置 换检验本身所造成的。这并不是仅仅从 M的大小上可 以判断出来的,我们需要知道异常值部分所占的比例 进而对其进行估算。对于决定异常值个数的指标 6: 40-44. torey, R. Tibrashini. Statistical significance for geno- mewide studies. Proceedings of the National Academy of Scien- 100(1): 9440-9445. sion of TMPRSS2 and ETS tran- scription factor genes in prostate cancer. Science, 2005, 310(5748): Chinnaiyan. Genomic outlier profile analysis: - cs, 2008, 9: 411-418. elrotein overo- 2001, 20: 1455-1464. k, 是否可以将其同M综合考虑进行筛选,如果考虑进来 会不会对结果有进一步的改善,诸如中位数、均值等 数字指标是否对我们有用,都是今后值得进一步探讨 的问题。 参考文献 (References) [1] R. Graham. DNA chips: State-of-the art. Nature Biotechnology, 1998, 1 [2] J. D. S ces of the United States of America, 2003, [3] S. A. Tomlins, et al. Recurrent fu 644-648. [4] D. Ghosh, A. M. mixture models, null hypotheses, and nonparametric estimation. Biostatistics, 2009, 10: 60-69. [5] R. Tibshirani, T. Hastie. Outlier sums for differential gene ex pression analysis. Biostatistics, 2007, 8: 2-8. [6] H. Lian. MOST: Detecting cancer differential gene expression. Biostatisti [7] 茆诗松, 王静龙, 濮晓龙. 高等数理统计(第二版)[M]. 北京: 高等教育出版社, 2006. M. West, et al. Predicting the[8] clinical status of human breast cancer by using gene expression profiles. Proceedings of the National Academy of Sciences of the United States of America, 2001, 98: 11462-11467. P. Benedit, et al. PTOV1, a nov[9] pexpressed in pr state cancer containing a new class of protein homology blocks. Nature Publishing Group, [10] Y. Oka, et al. M6P/IGF2R tumor suppressor gene mutated in hepatocellular carcinomas in Japan. Hepatology, 2002, 35(5): 1153- 1163. Copyright © 2011 Hanspub HJCB |