轮图的强连通性 The Strong Connectivity of the Wheel Network

doi:10.12677/AAM.2023.126305

Advances in Applied Mathematics
Vol. 12 No. 06 ( 2023 ), Article ID: 68127 , 16 pages
10.12677/AAM.2023.126305

轮图的强连通性

王苏，王世英

●How to Cite this Article

山西师范大学数学与计算机科学学院，山西太原

收稿日期：2023年5月28日；录用日期：2023年6月23日；发布日期：2023年6月30日

摘要

互连网络在大型多处理器系统中扮演着重要的角色，许多多处理器系统都有互连网络作为底层拓扑，网络通常用图来表示。在处理器及其彼此之间的通信链路可能发生故障的系统中，重要的是要考虑网络的容错能力。在此背景下，提出了网络的强连通性。为了实现强连通性，它允许处理器和通信链路同时发生故障。一个图G的强0-好邻连通性也称为图G的强连通性，同时我们把一个图G的强1-好邻连通性也称为图G的强自然连通性。本文在n-维泡型星图BS_n强连通性的基础上研究了当n ≥ 4时，CW_n的一些强连通性，其中包括CW_n的强0-好邻连通性、强自然连通性以及强自然边连通性等相关性质。

关键词

互连网络，强连通性，连通性，轮图

The Strong Connectivity of the Wheel Network

Su Wang, Shiying Wang

School of Mathematics and Computer Science, Shanxi Normal University, Taiyuan Shanxi

Received: May 28^th, 2023; accepted: Jun. 23^rd, 2023; published: Jun. 30^th, 2023

ABSTRACT

Interconnect network plays an important role in large multiprocessor system, many multiprocessor systems have an interconnect network as the underlying topology, and the network is usually represented by a graph. In systems where the processors and their communication links to each other can fail, it is important to consider the fault tolerance of the network. Under this background, the strong connectivity of network is proposed. To achieve strong connectivity, it allows both the processor and the communication link to fail simultaneously. The strong 0-good-neighbor connectivity of a graph G is also called the strong connectivity of a graph G, and the strong 1-good-neighbor connectivity of a graph G is also called the strong natural connectivity of a graph G. In this paper, based on the strong connectivity property of n-dimensional bubble-sort star graph BS_n, we study some strong connectivity of CW_n for n ≥ 4, including the strong 0-good-neighbor connectivity, strong natural connectivity and strong natural edge connectivity of CW_n and soon.

Keywords:Interconnection Networks, Strong Connectivity, Connectivity, Wheel Networks

This work is licensed under the Creative Commons Attribution International License (CC BY 4.0).

http://creativecommons.org/licenses/by/4.0/

1. 引言

近年来，海量数据处理和复杂问题的解决对多处理器系统的性能要求越来越高。许多多处理器系统都有互连网络(简称网络)作为底层拓扑，因此互连网络这一课题得到了广泛的研究。互连网络的体系结构通常表示为无向图G，其中顶点表示处理器，边表示连接两个不同处理器的通信链路。设 $G = (V, E)$ 是一个图，其中顶点集为 $V (G)$ ，边集为 $E (G)$ 。相应地，我们用 $| V (G) |$ 和 $| E (G) |$ 分别表示图G的顶点数和边数。对于一个非空顶点集 $V^{'} \subset V (G)$ ，G中 $V^{'}$ 的诱导子图记为 $G [V^{'}]$ ，该图的顶点集是 $V^{'}$ ，边集是G的所有端点都在 $V^{'}$ 中的边的集合。顶点x的度 $d_{G} (x)$ 表示的是与x相连的边的条数。对于图G的任意一个顶点x， $N_{G} (x)$ 定义为与x相邻的所有顶点的集合，并且我们用 $d_{G} (x)$ 表示 $N_{G} (x)$ 的基数。如果 $u \in N_{G} (x)$ ，则u称为x的邻点。对于顶点集 $X \subseteq V$ ，X的邻域定义为 $N_{G} (X) = {\cup_{x \in X} N_{G} (x)} - X$ 。特别地，如果x是G的一个孤立点，则 $d_{G} (x) = 0$ 。G的最大度用 $Δ (G)$ 表示，G的最小度用 $δ (G)$ 表示。对于邻域和度，当没有混淆时，我们通常会省略图的下标。如果对于图G的任意一个顶点v，都有 $d_{G} (v) = k$ ，则图G称为k-正则图。

互连网络决定了多处理器系统的性能。在节点及其链路可能发生故障的系统中，考虑网络的容错能力是很重要的。大型网络的容错能力通常衡量的是在网络拓扑中发生一定数量的节点故障和链路故障时，网络能在多大程度上保持其原始性质。在此背景下，提出了网络的强连通性。强连通性是在连通性的基础上衍生出来的产物，因此我们先对连通性进行简单的阐述。令 $G = (V, E)$ 是一个连通图，则图G的连通性(边连通性) $κ (G)$ ( $λ (G)$ )的一个基本定义是删除后产生不连通的图或平凡图的顶点(边)的最小数目。如果 $G - F$ 是不连通的或者只是一个孤立点，那么F是图G的一个点割，其中 $F \subseteq V (G)$ 。对于 $F \subseteq E (G)$ ，如果 $G - F$ 是不连通的，那么F是图G的一个边割。取一个故障集 $F \subseteq V$ ，如果对于 $V \ F$ 中的每一个顶点x，都有 $| N_{G} (x) \cap (V \ F) | \geq g$ ，则称F是一个g-好邻故障集。使得 $G - F$ 不连通的一个g-好邻故障集F被称为图G的一个g-好邻割。g-好邻割的最小基数称为图G的g-好邻连通度，用 $κ^{(g)} (G)$ 表示。如果 $G - F$ 的每个分支至少有 $(g + 1)$ 个顶点，则称故障集 $F \subseteq V$ 是一个g-额外故障集。使得 $G - F$ 不连通的一个g-额外故障集F被称为图G的一个g-额外割。g-额外割的最小基数称为图G的g-额外连通度，用 ${\tilde{κ}}^{(g)} (G)$ 表示。本文主要研究的是当 $n \geq 4$ 时， $C W_{n}$ 的一些强连通性。在本文中，我们首先得到了 $C W_{n}$ 的强连通度。在此基础上，同时我们也研究了当条件改变时 $(g = 1)$ 的各类连通性的结论。而强连通性的有关概念和性质，我们将在下一部分详细给出。

2. 预备知识

2.1. 轮图

在置换 $(\begin{array}{l} \begin{matrix} 1_{} & 2_{} & \dots & n_{} \end{matrix} \\ \begin{matrix} p_{1} & p_{2} & \dots & p_{n} \end{matrix} \end{array})$ 中， $i \to p_{i}$ ，为了方便用 $p_{1} p_{2} \dots p_{n}$ 表示置换 $(\begin{array}{l} \begin{matrix} 1_{} & 2_{} & \dots & n_{} \end{matrix} \\ \begin{matrix} p_{1} & p_{2} & \dots & p_{n} \end{matrix} \end{array})$ 。每个置换都可以用不相交的轮换的乘积表示。例如， $(\begin{array}{l} \begin{matrix} 1 & 2 & 3 \end{matrix} \\ \begin{matrix} 2 & 3 & 1 \end{matrix} \end{array}) = (123)$ 。特别地， $(\begin{array}{l} \begin{matrix} 1 & 2 & \dots & n \end{matrix} \\ \begin{matrix} 1 & 2 & \dots & n \end{matrix} \end{array}) = (1)$ 。两个置换的乘积 $σ τ$ 是先作用于 $τ$ 后作用于 $σ$ 的复合函数，例如， $(12) (13) = (132)$ 。对于这里未定义的术语和符号，我们则遵循 [1] 。

下面对轮图 $C W_{n}$ 的定义进行简单介绍。轮图 $C W_{n}$ 是一个有 $n!$ 个顶点的图，并且每个顶点都有 $x = x_{1} x_{2} \dots x_{n}$ 的形式，其中 $1 \leq x_{i} \leq n$ ，并且对于不同的 $1 \leq i, j \leq n$ ，有 $x_{i} \neq x_{j}$ 。我们定义一个运算“ $\circ$ ”，该运算使得 $x = y \circ (i, j)$ ，例如 $x = x_{1} x_{2} \dots x_{i} \dots x_{j} \dots x_{n}$ ，那么 $y = x_{1} x_{2} \dots x_{j} \dots x_{i} \dots x_{n}$ ，其中 $x, y \in V (C W_{n})$ 。两个不同的顶点 $x, y \in V (C W_{n})$ ， $(x, y) \in E (C W_{n})$ 当且仅当 $x = y \circ (1, i)$ ，且 $2 \leq i \leq n$ ，或者 $x = y \circ (i, i + 1)$ ，且 $2 \leq i \leq n - 1$ ，或者 $x = y \circ (2, n)$ (见 [2] )。 $C W_{n}$ 可以划分为n个子图 $C W_{n}^{1}, C W_{n}^{2}, \dots, C W_{n}^{n}$ ，其中每个 $C W_{n}^{i}$ 在标签字符串的最后一个位置都有一个固定的i，每个 $C W_{n}^{i}$ 同构于 $B S_{n - 1}$ ，且 $1 \leq i \leq n$ 。注意 $C W_{n}$ 和 $B S_{n}$ 都是特殊的Cayley图。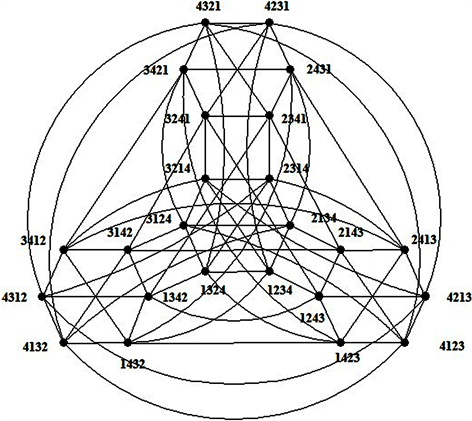轮图 $C W_{4}$ 如图1所示。

Figure 1. The wheel network CW₄

图1. 轮图CW₄

2.2. 定义和性质

定义2.1 ( [3] ) 设 $G = (V, E)$ 是一个非平凡连通图，如果 $δ (G - F) \geq g$ ，则强故障集 $F \subseteq V \cup E$ 称为强g-好邻故障集。使得 $G - F$ 不连通的一个强g-好邻故障集F被称为图G的一个强g-好邻割。强g-好邻割的最小基数称为图G的强g-好邻连通度，用 $κ λ^{(g)} (G)$ 表示。若图G有一个强g-好邻割，则连通图G是强g-好邻连通的。图G的强 -好邻连通度也称做图G的强连通度，记为 $κ λ (G)$ ，图G的强 -好邻连通度也称做图G的强自然连通度，记为 $n κ λ (G)$ 。若 $F \subseteq E$ ，则图G的强自然连通度称为图G的自然边连通度，表示为 $n λ (G)$ 。

假设 $g^{'} \geq g$ 。如果一个连通图G是强 $g^{'}$ -好邻连通的，那么图G有一个强 $g^{'}$ -好邻割F。因此可以得到 $δ (G - F) \geq g^{'}$ ，再结合 $g^{'} \geq g$ ，我们有 $δ (G - F) \geq g$ 。因此，图G也是强g-好邻连通的。由此我们有下述定理成立。

定理2.2 ( [3] ) 令 $g^{'} \geq g$ ，且G是一个强 $g^{'}$ -好邻连通图。那么 $κ λ^{(g^{'})} (G) \geq κ λ^{(g)} (G)$ 。

定义2.3 ( [3] ) 设 $G = (V, E)$ 是一个非平凡连通图，如果 $G - F$ 的每个分支至少有 $g + 1$ 个顶点，则强故障集 $F \subseteq V \cup E$ 称为强g-额外故障集。使得 $G - F$ 不连通的一个强g-额外故障集F被称为图G的一个强g-额外割。强g-额外割的最小基数称为图G的强g-额外连通度，用 $\tilde{κ} λ^{(g)} (G)$ 表示。若图G有一个强g-额外割，则连通图G是强g-额外连通的。

假设 $g^{'} \geq g$ 。如果一个连通图G是强 $g^{'}$ -额外连通的，那么图G有一个强 $g^{'}$ -额外割F。因此可以得到 $G - F$ 的每个分支至少有 $g^{'} + 1$ 个顶点，再结合 $g^{'} \geq g$ ，我们有 $G - F$ 的每个分支至少有 $g + 1$ 个顶点。因此，图G也是强g-额外连通的。由此我们有下列定理成立。

定理2.4 ( [3] ) 令 $g^{'} \geq g$ ，且G是一个强 $g^{'}$ -额外连通图。那么 $\tilde{κ} λ^{(g^{'})} (G) \geq \tilde{κ} λ^{(g)} (G)$ 。

定理2.5 ( [3] ) 令G是一个强g-好邻连通图，那么 $κ λ^{(g)} (G) \geq \tilde{κ} λ^{(g)} (G)$ 。

定理2.6 ( [3] ) 令G是一个强g-额外连通图，当 $g = 0, 1$ 时，有 $κ λ^{(g)} (G) = \tilde{κ} λ^{(g)} (G)$ 。

定理2.7 ( [3] ) 对于任何整数 $n \geq 2$ ， $κ λ (B S_{n}) = 2 n - 3$ 。

定理2.8 ( [4] ) 令 $n \geq 3$ ，令 $F \subseteq E (B S_{n})$ 且 $| F | \leq 4 n - 9$ 。如果 $B S_{n} - F$ 是不连通的，则 $B S_{n} - F$ 有两个分支，其中一个是孤立点。

定理2.9 ( [5] ) 对于任何整数 $n \geq 4$ ，泡型星图 $B S_{n}$ 是紧 $(2 n - 3)$ 超连通的。

定理2.10 ( [3] ) 对于任何整数 $n \geq 2$ ，泡型星图 $B S_{n}$ 是紧超 $(2 n - 3)$ 边连通的。

定理2.11 ( [3] ) 对于任何整数 $n \geq 3$ ，泡型星图 $B S_{n}$ 是超自然 $(4 n - 8)$ 边连通的。

定理2.12 ( [3] ) 对于任何整数 $n \geq 4$ ，泡型星图 $B S_{n}$ 是强紧超 $(2 n - 3)$ 连通的。

在这一部分中，我们通常假设 $n \geq 4$ ，并且根据最后一个位置的标签字符串对 $C W_{n}$ 进行划分，其中 $1 \leq i \leq n$ 。定义 $E_{i, j} (C W_{n}) = E_{C W_{n}} (V (C W_{n}^{i}), V (C W_{n}^{j}))$ ，其中 $i, j \in [1, n]$ 且 $i \neq j$ 。对于任意 $x \in V (C W_{n}^{i})$ ，我们定义 $x^{+} = x \circ (1, n)$ ， $x^{-} = x \circ (n - 1, n)$ ， $x^{*} = x \circ (2, n)$ ，它们被称为x的外部邻域。并且令 $N_{x}^{+} = {x^{+}, x^{-}, x^{*}}$ 。 $C W_{n}$ 有以下性质。

命题1 ( [6] ) 对于任何整数 $n \geq 4$ ， $C W_{n}$ 是 $(2 n - 2)$ -正则的，是点传递的。

命题2 ( [6] ) 对于任何整数 $n \geq 4$ ， $C W_{n}$ 是二部图。

命题3 ( [7] ) 对于任何整数 $n \geq 4$ ， $C W_{n}$ 的围长是4。

命题4 ( [7] [8] ) 1) 对于 $i, j \in [1, n]$ 且 $i \neq j$ ， $| E_{i, j} (C W_{n}) | = 3 (n - 2)!$ ；

2) 对于 $x, y \in V (C W_{n}^{i})$ ， $N_{x}^{+} \cap N_{y}^{+} = 0$ ；

3) 对于 $x, y \in V (C W_{n})$ ， $| N_{C W_{n}} (x) \cap N_{C W_{n}} (y) | \leq 3$ 。

命题5 ( [7] ) 令 $x \in V (C W_{n}^{i})$ 且 $i \in [1, n]$ ，则 $x^{+}$ ， $x^{-}$ ， $x^{*}$ 属于三个不同的 $C W_{n}^{l}^{'} s$ ，并且 $i \neq l$ 。

命题6 ( [7] [8] ) 若 $x \in V (C W_{n}^{[1, 3]})$ ，那么 $x^{+} \in V (C W_{n}^{[4, n]})$ ，或者 $x^{-} \in V (C W_{n}^{[4, n]})$ ，或者 $x^{*} \in V (C W_{n}^{[4, n]})$ 。

命题7 ( [4] [9] ) 对于 $n \geq 4$ ， $κ (B S_{n}) = 2 n - 3$ ， $λ (B S_{n}) = 2 n - 3$ 。

命题8 ( [6] [7] ) 对于 $n \geq 4$ ， $κ (C W_{n}) = 2 n - 2$ ， $λ (C W_{n}) = 2 n - 2$ 。

命题9 ( [9] ) 对于 $n \geq 4$ ，令 $F \subseteq V (B S_{n})$ 且 $| F | \leq 4 n - 9$ 。如果 $B S_{n} - F$ 是不连通的，则 $B S_{n} - F$ 满足以下情形之一：

1) $B S_{n} - F$ 有两个分支，其中一个分支是孤立点；

2) $B S_{n} - F$ 有三个分支，其中两个分支是孤立点。

命题10 ( [3] ) 对于 $n \geq 3$ ，令 $F \subseteq V (B S_{n}) \cup E (B S_{n})$ 且 $| F | \leq 4 n - 9$ 。如果 $B S_{n} - F$ 是不连通的，则 $B S_{n} - F$ 满足以下情形之一：

1) $B S_{n} - F$ 有两个分支，其中一个分支是孤立点；

2) $B S_{n} - F$ 有三个分支，其中两个分支是孤立点。

命题11 ( [4] ) 对于 $n \geq 3$ ，令 $F \subseteq E (B S_{n})$ 且 $| F | \leq 6 n - 14$ 。如果 $B S_{n} - F$ 是不连通的，则 $B S_{n} - F$ 中存在一个连通分支H使得 $| V (H) | \geq n! - | F | - 2$ 。

命题12 ( [4] ) 对于 $n \geq 3$ ，令 $F \subseteq E (B S_{3})$ 且 $| F | \leq 4$ 。如果 $B S_{3} - F$ 是不连通的，则 $B S_{3} - F$ 有两个分支，其中一个分支是一个孤立点或者一条边。

命题13 ( [7] ) 对于 $n \geq 5$ ，n-维轮图的自然连通度是 $4 n - 6$ 。

命题14 ( [10] ) 对于 $n \geq 4$ ，令 $F \subseteq V (B S_{n})$ 且 $| F | \leq 4 n - 10$ 。如果 $B S_{n} - F$ 是不连通的，则 $B S_{n} - F$ 中存在一个连通分支H使得 $| V (H) | \geq n! - | F | - 1$ 。

关于泡型星图 $B S_{n}$ 和n-维轮图 $C W_{n}$ 其他一些性质的研究，见参考文献 [11] [12] [13] [14] ，而关于本文的一些研究思想等，可参考文献 [3] [5] 以及 [15] [16] [17] [18] 等。

3. 轮图的强连通性

定理3.1 对于任何整数 $n \geq 4$ ， $κ λ (C W_{n}) = 2 n - 2$ 。

证明：令F是 $C W_{n}$ 的最小强割。若 $F \subseteq V (C W_{n})$ ，根据命题8，有 $| F | = 2 n - 2$ 。若 $F \subseteq E (C W_{n})$ ，根据命题8，有 $| F | = 2 n - 2$ 。故该定理的结果在上述情况中成立。因此，假设 $n \geq 4$ 且 $F ⊄ V (C W_{n})$ 。令 $F_{v} = F \cap V (C W_{n})$ ， $F_{v} \neq \emptyset$ ，并且令 $F_{e} = F \cap E (C W_{n})$ ， $F_{e} \neq \emptyset$ 。假设F是 $C W_{n}$ 的最小强割，且 $| F | \leq 2 n - 3$ 。因为 $| F_{v} | \leq 2 n - 4$ ，由命题得 $C W_{n} - F_{v}$ 是连通的。因为 $F_{e}$ 是 $C W_{n} - F_{v}$ 的最小边割，所以 $C W_{n} - F_{v} - F_{e}$ 有两个分支。令 $| F_{e} | = i$ 。因为 $n \geq 4$ ，所以 $n! - | F_{v} | \geq n! - (2 n - 3 - i) > 2 (i + 1)$ 成立。因此，在 $C W_{n} - F_{v} - F_{e}$ 中有一个分支C，使得 $| V (C) | \geq i + 1$ 。在C中，令顶点集 $V_{c}$ 是由在 $C W_{n} - F_{v}$ 与 $F_{e}$ 关联的顶点构成。因此 $| V_{c} | \leq | F_{e} | = i$ 。由于 $| V_{c} | + | F_{v} | \leq | F_{v} | + | F_{e} | = | F | \leq 2 n - 3$ ，故根据命题8，可得 $C W_{n} - F_{v} - F_{e}$ 是连通的。因此， $C W_{n} - F$ 是连通的，与F是 $C W_{n}$ 的最小强割矛盾。故 $| F | \geq 2 n - 2$ 。

令 $u = (1)$ ， $v = (12)$ ，并且令 $F = {(1, i) : 3 \leq i \leq n} \cup {(i, i + 1) : 2 \leq i \leq n - 1} \cup {(2, n)} \cup {u v}$ ，则F是 $C W_{n}$ 的一个强割。因此 $κ λ (C W_{n}) \leq 2 n - 2$ 。结合 $| F | \geq 2 n - 2$ ，我们有 $κ λ (C W_{n}) = 2 n - 2$ 。

4. 轮图的强自然连通性

引理4.1令 $F \subseteq V (C W_{4})$ 且 $| F | \leq 9$ 。如果 $C W_{4} - F$ 是不连通的，则 $C W_{4} - F$ 满足以下情形之一：

(1) $C W_{4} - F$ 有两个分支，其中分支一个是孤立点：

(2) $C W_{4} - F$ 有三个分支，其中分支两个是孤立点。

证明：根据命题8， $| F | \geq 6$ 。令 $F_{i} = F \cap V (C W_{4}^{i})$ ，其中 $i \in [1, 4]$ 且 $| F_{1} | \geq | F_{2} | \geq | F_{3} | \geq | F_{4} |$ 。由 $| F | \leq 9$ ，则 $| F_{4} | \leq 2$ ，我们首先证明以下声明。

声明1：对于一些 $i \in [1, 3]$ ，如果 $| F_{i} | \leq 2$ ，那么 $C W_{4} [V (C W_{_{4}}^{i} - F_{i}) \cup V (C W_{4}^{4} - F_{4})]$ 是连通的。

声明1的证明：根据命题7和对于 $i \in [1, 3]$ ， $C W_{4}^{i} ≅ B S_{3}$ ，则对于每个 $j \in [i, 3]$ ， $C W_{4}^{j} - F_{j}$ 是连通的。并且 $| E_{p, 4} (C W_{4}) | = 6 > 4 \geq | F_{p} | + | F_{4} |$ ，其中 $p \in [i, 3]$ ，这意味着 $E_{p, 4} (C W_{4} - F) \neq \emptyset$ 。因此， $C W_{4} [V (C W_{_{4}}^{i} - F_{i}) \cup V (C W_{4}^{4} - F_{4})]$ 是连通的。

声明2： $| F_{4} | \geq 1$

声明2的证明：若 $F_{4} = \emptyset$ ，则 $C W_{4}^{4} - F_{4}$ 是连通的。根据命题6，可以得到 $C W_{4} - F$

是连通的，这与假设矛盾。

根据声明1和假设，则 $| F_{1} | \geq 3$ 。根据声明2，可得 $| F_{2} | \geq | F_{3} | \geq 1$ ，并且由 $| F | \leq 9$ ，则 $| F_{1} | \leq 6$ 。

如果 $| F_{1} | = 3$ ，那么 $| F_{2} | + | F_{3} | + | F_{4} | \leq 6$ ，并且根据命题5可得，在 $C W_{4} - F$ 中有一条边连接 $C W_{4}^{1} - F_{1}$ 和 $C W_{4} [V (C W_{4}^{2} - F_{2}) \cup V (C W_{4}^{3} - F_{3}) \cup V (C W_{4}^{4} - F_{4})]$ 。

a) 如果 $| F_{2} | \leq 2$ ，那么根据声明1， $C W_{4} [V (C W_{4}^{2} - F_{2}) \cup V (C W_{4}^{3} - F_{3}) \cup V (C W_{4}^{4} - F_{4})]$ 是连通的。因此根据假设可得 $C W_{4}^{1} - F_{1}$ 是不连通的。令 $x_{1}, x_{2}, x_{3}$ 是 $C W_{4}^{1} - F_{1}$ 的三个孤立点，并且令 $X = {x_{i} : x_{i}$ 是 $C W_{4} - F$ 的孤立点，其中 $i \in [1, 3]}$ ，那么根据命题4(2)， $3 | X | \leq | F_{2} | + | F_{3} | + | F_{4} |$ ，即 $| X | \leq 2$ 。因此，如果 $| X | = 1$ ，那么 $C W_{4} - F$ 满足(1)；如果 $| X | = 2$ ，则 $C W_{4} - F$ 满足(2)。

b) 如果 $| F_{2} | = 3$ ，那么 $| F_{3} | \leq 2$ ，且 $| F_{4} | = 1$ 。根据声明1，我们可以得到 $C W_{4} [V (C W_{4}^{3} - F_{3}) \cup V (C W_{4}^{4} - F_{4})]$ 是连通的。因为 $| E_{i, 4} (C W_{4}) | = 6 > 4 \geq | F_{i} | + | F_{4} |$ ，其中 $i \in [1, 2]$ ，所以 $| E_{i, 4} (C W_{4} - F) | \neq 0$ 。因此，根据假设，对于某些 $i \in [1, 2]$ ， $C W_{4}^{i} - F_{i}$ 是不连通的。不失一般性，我们假设 $C W_{4}^{2} - F_{2}$ 是不连通的。令 $y_{1}, y_{2}, y_{3}$ 是 $C W_{4}^{2} - F_{2}$ 的三个孤立点，并且令 $Y = {y_{i} : y_{i}$ 是 $C W_{4} - F$ 的孤立点，其中 $i \in [1, 3]}$ ，那么根据命题4(2)，得到 $3 | Y | \leq | F_{1} \ F_{2} |$ ，即 $| Y | \leq 2$ 。因此，如果 $| Y | = 1$ ，那么 $C W_{4} - F$ 满足(1)；如果 $| Y | = 2$ ，则 $C W_{4} - F$ 满足(2)。如果 $C W_{4}^{1} - F_{1}$ 和 $C W_{4}^{2} - F_{2}$ 都不连通，当 $| X | = 1$ 且 $| Y | = 1$ 时， $C W_{4} - F$ 满足(2)。

如果 $| F_{1} | = 4$ ，那么根据声明2， $| F_{2} | \leq 3$ 。

a) 如果 $| F_{2} | \leq 2$ ，那么根据声明1， $C W_{4} [V (C W_{4}^{2} - F_{2}) \cup V (C W_{4}^{3} - F_{3}) \cup V (C W_{4}^{4} - F_{4})]$ 是连通的。因此，根据假设， $C W_{4}^{1} - F_{1}$ 是不连通的，并且 $| E_{1, 4} (C W_{4}) | = 6 > 5 \geq | F_{1} | + | F_{4} |$ ，那么 $C W_{4} - F$ 满足(1)。

b) 如果 $| F_{2} | = 3$ ，那么 $| F_{3} | = | F_{4} | = 1$ 。然后根据声明1，可以得到 $C W_{4} [V (C W_{4}^{3} - F_{3}) \cup V (C W_{4}^{4} - F_{4})]$ 是连通的。因为 $| E_{1, 4} (C W_{4}) | = 6 > 5 \geq | F_{1} | + | F_{4} |$ 且 $| E_{1, 4} (C W_{4}) | = 6 > 5 \geq | F_{1} | + | F_{4} |$ ，所以 $| E_{1, 4} (C W_{4} - F) | \neq 0$ 和 $| E_{2, 4} (C W_{4} - F) | \neq 0$ 。因此，根据假设，对于某些 $i \in [1, 2]$ ， $C W_{4}^{i} - F_{i}$ 是不连通的。不失一般性，我们假设 $C W_{4}^{2} - F_{2}$ 是不连通的。令 $y_{1}, y_{2}, y_{3}$ 是 $C W_{4}^{2} - F_{2}$ 的三个孤立点，并且令 $Y = {y_{i} : y_{i}$ 是 $C W_{4} - F$ 的孤立点，其中 $i \in [1, 3]}$ ，那么根据命题4(2)，得到 $3 | Y | \leq | F_{1} \ F_{2} |$ ，即 $| Y | \leq 2$ 。因此，如果 $| Y | = 1$ ，那么 $C W_{4} - F$ 满足(1)；如果 $| Y | = 2$ ，则 $C W_{4} - F$ 满足(2)。如果 $C W_{4}^{1} - F_{1}$ 和 $C W_{4}^{2} - F_{2}$ 都不连通，当 $| X | = 1$ 且 $| Y | = 1$ 时， $C W_{4} - F$ 满足(2)。

如果 $5 \leq | F_{1} | \leq 6$ ，那么根据声明2， $| F_{2} | \leq 2$ 。再由声明1，可以得到 $C W_{4} [V (C W_{4}^{2} - F_{2}) \cup V (C W_{4}^{3} - F_{3}) \cup V (C W_{4}^{4} - F_{4})]$ 是连通的。但是根据命题5，当 $| F_{1} | = 5$ 时 $C W_{4} - F$ 满足(1)；当 $| F_{1} | = 6$ 时，可得 $C W_{4} - F$ 是连通的，矛盾。

引理4.2 当 $n \geq 4$ ，令 $F \subseteq V (C W_{n})$ 且 $| F | \leq 4 n - 7$ 。如果 $C W_{n} - F$ 是不连通的，那么 $C W_{n} - F$ 满足以下情形之一：

(1) $C W_{n} - F$ 有两个分支，其中一个分支是孤立点；

(2) $C W_{n} - F$ 有三个分支，其中两个分支是孤立点。

证明：根据引理4.1，当 $n = 4$ 时，结果成立。下证当 $n \geq 5$ 时，结果成立。现在我们假设对于任何 $F \subseteq V (C W_{n})$ ，且 $| F | \leq 4 n - 7$ ， $C W_{n} - F$ 是不连通的。根据命题8， $| F | \geq 2 n - 2$ 。令 $F_{i} = F \cap V (C W_{n}^{i})$ ， $| F_{1} | \geq | F_{2} | \geq \dots \geq | F_{n} |$ ，其中 $i \in [1, n]$ 。

声明3： $1 \leq | F_{4} | \leq 2 n - 6$

声明3的证明：如果 $F_{4} = \emptyset$ ，那么 $F_{5} = F_{6} = \dots = F_{n} = \emptyset$ ，因此，根据命题4(1)， $C W_{n} [V (C W_{n}^{4} - F_{4}) \cup V (C W_{n}^{5} - F_{5}) \cup \dots \cup V (C W_{n}^{n} - F_{n})]$ 是连通的，那么根据命题6， $C W_{n} - F$ 是连通的，矛盾。如果 $| F_{4} | \geq 2 n - 5$ ，则 $| F | \geq 4 (2 n - 5) > 4 n - 7$ ，这与 $| F | \leq 4 n - 7$ 是矛盾的。

根据声明3，对于每个 $i \in [4, n]$ ， $C W_{n}^{i} - F_{i}$ 是连通的，并且 $| F_{2} | \geq | F_{3} | \geq | F_{4} | \geq 1$ 。因此，由于 $| F | \leq 4 n - 7$ ，我们可以得到 $| F_{1} | \leq 4 n - 10$ 。同时 $1 \leq | F_{3} | \leq 2 n - 6$ ，否则的话 $| F | \geq 3 (2 n - 5) + 1 > 4 n - 7$ ，这与 $| F | \leq 4 n - 7$ 是矛盾的。注意， $| E_{i, j} (C W_{n} - F) | \geq 3 (n - 2)! - (4 n - 7) > 1$ ，其中 $i, j \in [1, n]$ 且 $n \geq 5$ 。因此在每对 $C W_{n}^{i} - F_{i}$ 之间都有一条边连接，其中 $i \in [1, n]$ 。那么根据 $C W_{n} - F$ 是不连通的，我们可以得到对于某些 $j \in [1, 2]$ ， $C W_{n}^{j} - F_{j}$ 是不连通的。不失一般性，我们假设 $C W_{n}^{1} - F_{1}$ 是不连通的，并且令 $C_{1}^{1}, \dots, C_{1}^{a}$ 是 $C W_{n}^{1} - F_{1}$ 的非平凡分支， $x_{1}, \dots, x_{b}$ 是 $C W_{n}^{1} - F_{1}$ 的孤立点。令 $X = {x_{i} : x_{i}$ 是 $C W_{n} - F$ 的孤立点，其中 $i \in [1, b]}$ 。注意，如果 $x_{i}$ 是 $C W_{n} - F$ 的孤立点，那么 $N_{x_{i}}^{+} \subseteq F \ F_{1}$ 。因此根据命题4(2)， $3 | X | \leq | F_{2} | + | F_{3} | + \dots + | F_{n} |$ 。

如果 $C W_{n}^{2} - F_{2}$ 是连通的，那么 $C W_{n} [V (C W_{n}^{2} - F_{2}) \cup V (C W_{n}^{3} - F_{3}) \cup \dots \cup V (C W_{n}^{n} - F_{n})]$ 是连通的。

a) 如果 $| F_{1} | \leq 4 n - 13$ ，根据命题9，则 $a = 1$ 且 $1 \leq b \leq 2$ 。另一方面，当 $n \geq 5$ 时， $| (N (C_{1}^{1})) \cap (V (C W_{n}^{2}) \cup V (C W_{n}^{3}) \cup \dots \cup V (C W_{n}^{n})) | \geq 3 ((n - 1)! - | F_{1} | - 2) - (| F | - | F_{1} |) \geq 3 (n - 1)! - (12 n - 31) \geq 39$ ，即在 $C W_{n} - F$ 中有一条边连接 $C_{1}^{1}$ 和 $C W_{n} [V (C W_{n}^{2} - F_{2}) \cup V (C W_{n}^{3} - F_{3}) \cup \dots \cup V (C W_{n}^{n} - F_{n})]$ 。因此 $C W_{n} - F$ 满足(1)或者(2)。

b) 如果 $| F_{1} | \geq 4 n - 12$ ，那么 $| F_{2} | + | F_{3} | + \dots + | F_{n} | \leq 5$ ，因此， $3 | X | \leq | F_{2} | + | F_{3} | + \dots + | F_{n} | \leq 5$ ，即 $| X | \leq 1$ 。由 $| N (V (C_{1}^{i})) \cap (V (C W_{n}^{2}) \cup V (C W_{n}^{3}) \cup \dots \cup V (C W_{n}^{n})) | \geq 3 | C_{1}^{i} | - | F \ F_{1} | \geq 6 - 5 = 1$ ，其中 $1 \leq a \leq i$ ，即在 $C W_{n} - F$ 中有一条边连接 $C_{1}^{i}$ 和 $C W_{n} [V (C W_{n}^{2} - F_{2}) \cup V (C W_{n}^{3} - F_{3}) \cup \dots \cup V (C W_{n}^{n} - F_{n})]$ 。进一步，根据假设，我们得到 $| X | = 1$ 。因此 $C W_{n} - F$ 满足(1)。

如果 $C W_{n}^{2} - F_{2}$ 是不连通的，根据命题7，能够得到 $| F_{2} | \geq 2 n - 5$ ，并且根据声明3，有 $| 4 n - 7 | \geq | F | \geq | F_{1} | + | F_{2} | + | F_{3} | + | F_{4} | \geq 2 (2 n - 5) + 1 + 1$ ，这意味着 $| F_{1} | \leq 2 n - 4$ 且 $| F_{2} | \geq 2 n - 5$ 。因此 $a = b = 1$ (如果 $b = 2$ ，那么当 $n \geq 5$ 时， $| F_{1} | \geq 2 (2 n - 5) - 3 = 4 n - 13 > 2 n - 4$ ，矛盾)，并且因为 $C W_{n}$ 是 $(2 n - 5)$ -正则的，所以 $C W_{n}^{2} - F_{2}$ 包含一个非平凡分支 $C_{2}^{1}$ 和一个孤立点w。注意 $| (N (C_{1}^{1})) \cap (V (C W_{n}^{3}) \cup V (C W_{n}^{4}) \cup \dots \cup V (C W_{n}^{n})) | \geq 3 ((n - 1)! - | F_{1} | - 1) - (| F_{3} | + | F_{4} | + \dots + | F_{n} |) > 1$ ， $| (N (C_{2}^{1})) \cap (V (C W_{n}^{3}) \cup V (C W_{n}^{4}) \cup \dots \cup V (C W_{n}^{n})) | \geq 3 ((n - 1)! - | F_{2} | - 1) - (| F_{3} | + | F_{4} | + \dots + | F_{n} |) > 1$ ，即在 $C W_{n} - F$ 有一条边连接 $C_{i}^{1}$ 和 $C W_{n} [V (C W_{n}^{3} - F_{3}) \cup V (C W_{n}^{4} - F_{4}) \cup \dots \cup V (C W_{n}^{n} - F_{n})]$ ，其中 $1 \leq i \leq 2$ 。如果 $(x_{1}, w) \in E (C W_{n})$ ，则当 $n \geq 5$ 时 $| F | = 2 (2 n - 3) = 4 n - 6 > 4 n - 7$ ，矛盾。因此 $C W_{n} - F$ 满足(2)当 $N_{x_{1}}^{+} \subseteq F$ 且 $N_{w}^{+} \subseteq F$ ，否则满足(1)。

引理4.3 设 $F \subseteq E (C W_{4})$ ，且 $| F | \leq 9$ 。如果 $C W_{4} - F$ 不连通，则 $C W_{4} - F$ 有两个分支，其中一个分支是一个孤立点。

证明：因为 $C W_{4} - F$ 是不连通的，不失一般性，假设 $| F_{1} | \geq | F_{2} | \geq | F_{3} | \geq | F_{4} |$ ，令 $C W_{4}$ 的所有交叉边为C，令 $F_{c} = F \cap C$ 。因为 $n = 4$ ，根据命题4(1)， $| E_{i, j} (C W_{4}) | = 6$ ，其中 $i, j \in [1, 4]$ ， $i \neq j$ 。由 $| F | \leq 9$ ，可得 $| F_{4} | \leq 2$ ；否则 $| F | \geq 3 \times 4 = 12$ ，与 $| F | \leq 9$ 相矛盾。根据命题7， $C W_{4} - F$ 是连通的。设H是 $C W_{4} - F$ 的包含 $C W_{4}^{4} - F_{4}$ 作为一个子集的连通部分。接下来我们考虑如下情况：

情况1： $| F_{1} | \leq 2$

在这种情形下，根据命题7， $C W_{4} - F$ 是连通的， $i \in [1, 4]$ 。现在我们声称 $| E_{1, 2} (C W_{4}) | - F \neq 0$ 或者 $| E_{1, 3} (C W_{4}) | - F \neq 0$ ；否则的话 $| F | \geq | E_{1, 2} (C W_{4}) | + | E_{1, 3} (C W_{4}) | = 12 > 9$ ，与 $| F | \leq 9$ 相矛盾。不失一般性，我们可以假设 $| E_{1, 2} (C W_{4}) | - F \neq 0$ 。相似的，可得 $| E_{1, i} (C W_{4}) | - F \neq 0$ ，或者 $| E_{2, i} (C W_{4}) | - F \neq 0$ ，其中 $i \in [3, 4]$ 。因此 $C W_{4} - F$ 是连通的，与假设相矛盾。

情况2： $| F_{1} | = 3$

假设 $| F_{2} | \leq 2$ ，则 $| F_{c} | \leq 6$ 。根据命题7， $C W_{4}^{i} - F_{i}$ 是连通的， $i \in [2, 4]$ 。我们可以得到 $| E_{2, 3} (C W_{4}) | - F \neq 0$ 或者 $| E_{2, 4} (C W_{4}) | - F \neq 0$ ；否则 $| F | \geq | E_{2, 3} (C W_{4}) | + | E_{2, 4} (C W_{4}) | = 12 > 9$ ，与 $| F | \leq 9$ 相矛盾。不失一般性，假设 $| E_{2, 3} (C W_{4}) | - F \neq 0$ 。因此 $C W_{4} [V (C W_{4}^{2}) \cup V (C W_{4}^{3}) \cup V (C W_{4}^{4})] - F$ 是H的一个子集。因为 $| F_{1} | = 3$ ，根据定理2.8， $C W_{4}^{1} - F_{1}$ 有一个连通分支 $H_{1}$ ，使得 $| V (H_{1}) | \geq 3! - 1$ 。因为 $| E_{1, 3} (C W_{4}) | - 2 (| V (C W_{4}^{1}) - V (H_{1}) |) - | F_{c} | \geq 12 - 2 - 9 > 0$ ，所以 $H_{1}$ 是H的一个子集。因此 $| V (H) | \geq 4! - 1$ 。

假设 $| F_{2} | = 3$ ，则 $| F_{c} | \leq 3$ 。如果 $| F_{3} | \leq 2$ ，根据命题7， $C W_{4}^{i} - F_{i}$ 是连通的， $i \in [3, 4]$ 。因为，所以 $C W_{4} [V (C W_{4}^{3}) \cup V (C W_{4}^{4})] - F$ 是H的一个子图。由命题6，对于任意的 $v \in V (C W_{4}^{1}) \cup V (C W_{4}^{2})$ ，存在两个顶点 $v_{1}, v_{2} \in {v^{+}, v^{-}, v^{*}}$ ，使得 $v_{1} \in V (C W_{4}^{3}) \cup V (C W_{4}^{4})$ 和 $v_{2} \in V (C W_{4}^{3}) \cup V (C W_{4}^{4})$ 。因为 $| F_{c} | \leq 3$ ，所以在 $C W_{4} [V (C W_{4}^{1}) \cup V (C W_{4}^{2})]$ 中最多有一个顶点不被包含在H中。因此 $| V (H) | \geq 4! - 1$ 。如果 $| F_{3} | = 3$ ，则 $| F_{c} | = 0$ 。根据命题6得， $H = C W_{4} - F$ 是连通的，与假设矛盾。

情况3： $| F_{1} | \geq 4$

假设 $| F_{2} | \leq 2$ ，则 $| F_{c} | \leq 5$ 。根据命题7， $C W_{4}^{i} - F_{i}$ 是连通的， $i \in [2, 4]$ 。因为 $| E_{i, j} (C W_{4}) | = 6 > 5$ ，其中 $i, j \in [2, 4]$ ， $i \neq j$ ，所以 $C W_{4} [V (C W_{4}^{3}) \cup V (C W_{4}^{4})] - F$ 是H的一个子图。已知对于任意的 $u \in V (C W_{4}^{1})$ ， ${u^{+}, u^{-}, u^{*}} \subseteq V (C W_{4}^{2}) \cup V (C W_{4}^{3}) \cup V (C W_{4}^{4})$ 。因为 $| F_{c} | \leq 5$ ，所以在 $V (C W_{4}^{1})$ 中最多有一个顶点不被包含在H中。因此 $| V (H) | \geq 4! - 1$ 。

假设 $| F_{2} | \geq 3$ ，则 $| F_{c} | \leq 2$ ， $| F_{3} | \leq 2$ 。根据命题7， $C W_{4}^{3} - F_{3}$ 。因为 $| E_{3, 4} (C W_{4}) - F | \geq 4$ ，所以 $C W_{4} [V (C W_{4}^{3}) \cup V (C W_{4}^{4})] - F$ 是H的一个子图。根据命题6，对于任意的 $v \in V (C W_{4}^{1}) \cup V (C W_{4}^{2})$ ，存在两个顶点 $v_{1}, v_{2} \in {v^{+}, v^{-}, v^{*}}$ ，使得 $v_{1} \in V (C W_{4}^{3}) \cup V (C W_{4}^{4})$ 和 $v_{2} \in V (C W_{4}^{3}) \cup V (C W_{4}^{4})$ 。因为 $| F_{c} | \leq 2$ ，所以在 $C W_{4} [V (C W_{4}^{1}) \cup V (C W_{4}^{2})]$ 中最多有一个顶点不被包含在H中。因此 $| V (H) | \geq 4! - 1$ 。

引理4.4设 $F \subseteq E (C W_{n})$ ，且 $| F | \leq 4 n - 7$ ， $n \geq 4$ 。如果 $C W_{n} - F$ 是不连通的，则 $C W_{n} - F$ 由两个分支组成，其中一个分支是一个孤立点。

证明：当 $n = 4$ 时，根据引理4.3，已证结论是成立的。下证当 $n \geq 5$ 时，结论成立。假设 $n \geq 5$ 且 $C W_{n} - F$ 是不连通的。不失一般性，我们可以假设 $| F_{1} | \geq | F_{2} | \geq \dots \geq | F_{n} |$ 。令 $C W_{n}$ 的所有交叉边为C，令 $F_{c} = F \cap C$ 。设H是 $C W_{n} - F$ 的包含 $C W_{n}^{n} - F_{n}$ 作为一个子集的连通部分。接下来我们考虑如下情况：

情况1： $| F_{1} | \leq 2 n - 6$

在这种情况下，根据命题7， $C W_{n}^{i} - F_{i}$ 是连通的， $i \in [1, n]$ 。因为 $n \geq 5$ ，所以 $3 (n - 2)! - (4 n - 7) > 0$ ，因此根据命题4(1)可得， $H = C W_{n} - F$ 是连通的，与假设 $C W_{n} - F$ 不连通相矛盾。

情况2： $2 n - 5 \leq | F_{1} | \leq 4 n - 13$

假设 $| F_{2} | \leq 2 n - 6$ ，则 $| F_{c} | \leq 2 n - 2$ 。根据命题7， $C W_{n}^{i} - F_{i}$ 是连通的， $i \in [2, n]$ 。因为 $n \geq 5$ ，所以 $3 (n - 2)! - (2 n - 2) > 0$ 。故， $C W_{n} [V (C W_{n}^{2}) \cup V (C W_{n}^{3}) \cup \dots \cup V (C W_{n}^{n})] - F$ 是H的一个子集。因为 $2 n - 5 \leq | F_{1} | \leq 4 n - 13$ ，根据命题11， $C W_{n}^{1} - F_{1}$ 有一个连通分支 $H_{1}$ ，使得 $| V (H_{1}) | \geq (n - 1)! - 1$ 。又因为 $| E_{c w_{n}} (V (H_{1}), V (C W_{n}^{2})) - F | \geq | E_{1, 2} (C W_{n}) | - (| V (C W_{n}^{1}) | - | V (H_{1}) |) - | F_{c} | \geq 3 (n - 2)! - 1 - (2 n - 2) > 0$ ，其中 $n \geq 5$ ，所以 $H_{1}$ 是H的一个子集。因此 $| V (H) | \geq n! - 1$ 。

假设 $| F_{2} | \geq 2 n - 5$ ，则 $| F_{c} | \leq 3$ ， $| F_{3} | \leq 3 < 2 n - 6$ ， $n \geq 5$ 。根据命题7， $C W_{n}^{i} - F_{i}$ 是连通的， $i \in [3, n]$ 。因为 $3 (n - 2)! > 3$ ，其中 $n \geq 5$ ， $C W_{n} [V (C W_{n}^{3}) \cup V (C W_{n}^{4}) \cup \dots \cup V (C W_{n}^{n})] - F$ 是H的一个子集。由命题6，对于任意的 $v \in V (C W_{4}^{1}) \cup V (C W_{4}^{2})$ ，存在两个顶点 $v_{1}, v_{2} \in {v^{+}, v^{-}, v^{*}}$ ，使得 $v_{1} \in V (C W_{n}^{3}) \cup V (C W_{4}^{4}) \cup \dots \cup V (C W_{n}^{n})$ 和 $v_{2} \in V (C W_{n}^{3}) \cup V (C W_{4}^{4}) \cup \dots \cup V (C W_{n}^{n})$ 。又 $| F_{c} | \leq 3$ ，所以在 $C W_{n} [V (C W_{n}^{1}) \cup V (C W_{n}^{2})]$ 中最多有一个顶点不被包含在H中。因此 $| V (H) | \geq n! - 1$ 。

情况3： $4 n - 12 \leq | F_{1} | \leq 4 n - 7$

在这种情况中，可得 $| F_{c} | \leq 5$ ， $| F_{3} | \leq 2 < 2 n - 6$ ， $n \geq 5$ ，根据命题7， $C W_{n}^{i} - F_{i}$ 是连通的， $i \in [3, n]$ 。因为 $3 (n - 2)! > 5$ ，其中 $n \geq 5$ ， $V (C W_{n}^{2}) \cup V (C W_{n}^{3}) \cup \dots \cup V (C W_{n}^{n})$ 是H的一个子集。

假设 $| F_{2} | \leq 2 n - 6$ ，则 $C W_{n} [V (C W_{n}^{2}) \cup V (C W_{n}^{3}) \cup \dots \cup V (C W_{n}^{n})] - F$ 是H的一个子集。已知对于任意的 $u \in V (C W_{n}^{1})$ ， ${u^{+}, u^{-}, u^{*}} \subseteq V (C W_{n}^{2}) \cup V (C W_{n}^{3}) \cup \dots \cup V (C W_{n}^{n})$ 。又因为 $| F_{c} | \leq 5$ ，所以在 $V (C W_{n}^{1})$ 中最多有一个顶点不被包含在H中。因此 $| V (H) | \geq n! - 1$ 。

假设 $| F_{2} | \geq 2 n - 5$ 。因为 $n \geq 5$ ，所以 $| F_{2} | \geq 5$ ，则 $| F_{c} | = 0$ 。根据命题6， $H = C W_{n} - F$ 是连通的，与假设相矛盾。

引理4.5 对于 $n \geq 4$ ，令 $F \subseteq V (C W_{n}) \cup E (C W_{n})$ 且 $| F | \leq 4 n - 7$ 。如果 $C W_{n} - F$ 是不连通的，则 $C W_{n} - F$ 满足以下情形之一：

(1) $C W_{n} - F$ 有两个分支，其中一个分支是孤立点；

(2) $C W_{n} - F$ 有三个分支，其中两个分支是孤立点。

证明：当 $n \geq 4$ 时，若 $F \subseteq V (C W_{n})$ 且 $| F | \leq 4 n - 7$ ，根据引理4.2得，在该情况下定理成立。若 $F \subseteq E (C W_{n})$ 且 $| F | \leq 4 n - 7$ ，根据引理4.4得，结论成立。因此，假设 $F \subseteq V (C W_{n}) \cup E (C W_{n})$ 且 $| F | \leq 4 n - 7$ ，其中 $F \cap V (C W_{n}) \neq \emptyset$ ， $F \cap E (C W_{n}) \neq \emptyset$ 。令 $F_{i} = F \cap V (C W_{n}^{i})$ ， $F_{i}^{e} = F \cap E (C W_{n}^{i})$ ，其中 $i \in [1, n]$ ，且 $| F_{1} \cup F_{1}^{e} | \geq | F_{2} \cup F_{2}^{e} | \geq \dots \geq | F_{n} \cup F_{n}^{e} |$ 。设C是 $C W_{n}$ 中的所有交叉边构成的集合，令 $F_{c} = F \cap C$ 。因此 $1 \leq | F_{1} | + | F_{2} | + \dots + | F_{n} | \leq 4 n - 8$ ， $1 \leq | F_{1}^{e} | + | F_{2}^{e} | + \dots + | F_{n}^{e} | \leq 4 n - 8$ 。当 $n = 4$ 时，如果 $| F | \leq 5$ ，根据命题8，那么 $C W_{4} - F$ 是连通的。当 $| F | = 5$ 时，由定理3.1得， $C W_{4} - F$ 有两个分支，其中一个分支是孤立点。因此，假设 $7 \leq | F | \leq 9$ ， $C W_{4} - F$ 是不连通的。我们考虑以下情况：

情况1： $| F_{1} | = 7$

在这种情况中， $C W_{4}^{i} ≅ B S_{3}$ ， $B S_{3} ≅ K_{3, 3}$ ，其中 $i \in [1, 4]$ 。

情况1.1： $5 \leq | F_{1} | \leq 6$

在该情形下， $5 \leq | F_{1} \cup F_{1}^{e} | \leq 7$ ，则 $0 \leq | F_{2} \cup F_{2}^{e} | + | F_{3} \cup F_{3}^{e} | + | F_{4} \cup F_{4}^{e} | + | F_{c} | \leq 2$ 。故，根据命题4(1)和命题7得 $C W_{4} - F$ 是连通的，矛盾。

情况1.2： $| F_{1} | = 4$

情况1.2.1： $5 \leq | F_{1} \cup F_{1}^{e} | \leq 7$

在该情形下， $0 \leq | F_{2} \cup F_{2}^{e} | + | F_{3} \cup F_{3}^{e} | + | F_{4} \cup F_{4}^{e} | + | F_{c} | \leq 2$ 。根据命题4(1)和命题7得， $C W_{4} [V (C W_{4}^{2} - F_{2} - F_{2}^{e}) \cup V (C W_{4}^{3} - F_{3} - F_{3}^{e}) \cup V (C W_{4}^{4} - F_{4} - F_{4}^{e})] - F_{c}$ 是连通的，根据命题5得， $C W_{4} - F$ 是连通的，矛盾。

情况1.2.2： $| F_{1} \cup F_{1}^{e} | = 4$

在本情况中， $| F_{2} \cup F_{2}^{e} | + | F_{3} \cup F_{3}^{e} | + | F_{4} \cup F_{4}^{e} | + | F_{c} | = 3$ ，而且 $| V (C W_{4}^{1} - F_{1} - F_{1}^{e}) | = 2$ 。

情况1.2.2.1： $| F_{2} \cup F_{2}^{e} | = 3$

根据 $| F_{1} \cup F_{1}^{e} | = 4$ 得， $| F_{3} \cup F_{3}^{e} | + | F_{4} \cup F_{4}^{e} | + | F_{c} | = 0$ 。故根据命题4(1)、 $C W_{4}^{i} ≅ B S_{3}$ 和命题7得， $C W_{4} [V (C W_{4}^{3} - F_{3} - F_{3}^{e}) \cup V (C W_{4}^{4} - F_{4} - F_{4}^{e})] - F_{c}$ 是连通的。再由命题5，我们可以得 $C W_{4} [V (C W_{4}^{1} - F_{1} - F_{1}^{e}) \cup V (C W_{4}^{3} - F_{3} - F_{3}^{e}) \cup V (C W_{4}^{4} - F_{4} - F_{4}^{e})] - F_{c}$ ， $C W_{4} [V (C W_{4}^{2} - F_{2} - F_{2}^{e}) \cup V (C W_{4}^{3} - F_{3} - F_{3}^{e}) \cup V (C W_{4}^{4} - F_{4} - F_{4}^{e})] - F_{c}$ 都是连通的。因此， $C W_{4} - F$ 是连通的，矛盾。

情况1.2.2.2： $| F_{j} \cup F_{j}^{e} | \leq 2$ ， $j \in [2, 4]$

由命题4(1)、7得， $C W_{4} [V (C W_{4}^{2} - F_{2} - F_{2}^{e}) \cup V (C W_{4}^{3} - F_{3} - F_{3}^{e}) \cup V (C W_{4}^{4} - F_{4} - F_{4}^{e})] - F_{c}$ 是连通的。因为 $| F_{2} \cup F_{2}^{e} | + | F_{3} \cup F_{3}^{e} | + | F_{4} \cup F_{4}^{e} | + | F_{c} | = 3$ ，所以由命题4(2)和命题5可知， $C W_{4} - F$ 是连通的(矛盾)或 $C W_{4} - F$ 有两个分支，其中一个分支是孤立点。

情况1.3： $| F_{1} | = 3$

情况1.3.1： $5 \leq | F_{1} \cup F_{1}^{e} | \leq 7$

通情况1.2.1的讨论方式类似，可得 $C W_{4} - F$ 是连通的，矛盾。

情况1.3.2： $| F_{1} \cup F_{1}^{e} | = 4$

本情况的讨论方法与情况1.2.2的讨论方法一致，同样可得 $C W_{4} - F$ 是连通的(矛盾)或 $C W_{4} - F$ 有两个分支，其中一个分支是孤立点。

情况1.3.3： $| F_{1} \cup F_{1}^{e} | = 3$

在这种情况中， $| F_{2} \cup F_{2}^{e} | + | F_{3} \cup F_{3}^{e} | + | F_{4} \cup F_{4}^{e} | + | F_{c} | = 4$ ，且 $| V (C W_{4}^{1} - F_{1} - F_{1}^{e}) | = 3$ 。

情况1.3.3.1： $| F_{2} \cup F_{2}^{e} | = 3$

根据 $| F_{1} \cup F_{1}^{e} | = 3$ 得， $| F_{3} \cup F_{3}^{e} | + | F_{4} \cup F_{4}^{e} | + | F_{c} | = 1$ 。故根据命题4(1)、 $C W_{4}^{i} ≅ B S_{3}$ 和命题7得， $C W_{4} [V (C W_{4}^{3} - F_{3} - F_{3}^{e}) \cup V (C W_{4}^{4} - F_{4} - F_{4}^{e})] - F_{c}$ 是连通的。再由命题5，我们可以得到 $C W_{4} [V (C W_{4}^{1} - F_{1} - F_{1}^{e}) \cup V (C W_{4}^{3} - F_{3} - F_{3}^{e}) \cup V (C W_{4}^{4} - F_{4} - F_{4}^{e})] - F_{c}$ ， $C W_{4} [V (C W_{4}^{2} - F_{2} - F_{2}^{e}) \cup V (C W_{4}^{3} - F_{3} - F_{3}^{e}) \cup V (C W_{4}^{4} - F_{4} - F_{4}^{e})] - F_{c}$ 都是连通的。因此， $C W_{4} - F$ 是连通的，矛盾。

情况1.3.3.2： $| F_{j} \cup F_{j}^{e} | \leq 2$ ， $j \in [2, 4]$

由命题4(1)、7得， $C W_{4} [V (C W_{4}^{2} - F_{2} - F_{2}^{e}) \cup V (C W_{4}^{3} - F_{3} - F_{3}^{e}) \cup V (C W_{4}^{4} - F_{4} - F_{4}^{e})] - F_{c}$ 是连通的。由于 $C W_{4}^{i} ≅ B S_{3}$ ， $B S_{3} ≅ K_{3, 3}$ ，如果 $C W_{4}^{1} - F_{1}$ 是不连通的，那么 $C W_{4}^{1} - F_{1}$ 是三个孤立点。由于 $| F_{2} \cup F_{2}^{e} | + | F_{3} \cup F_{3}^{e} | + | F_{4} \cup F_{4}^{e} | + | F_{c} | = 4$ ，则 $C W_{4} - F$ 是连通的(矛盾)或 $C W_{4} - F$ 有两个分支，其中一个分支是孤立点。

情况1.4： $1 \leq | F_{1} | \leq 2$

情况1.4.1： $5 \leq | F_{1} \cup F_{1}^{e} | \leq 7$

通情况1.2.1的讨论方式类似，可得 $C W_{4} - F$ 是连通的，矛盾。

情况1.4.2： $| F_{1} \cup F_{1}^{e} | = 4$

本情况的讨论方法与情况1.2.2的讨论方法一致，同样可得 $C W_{4} - F$ 是连通的(矛盾)或 $C W_{4} - F$ 有两个分支，其中一个分支是孤立点。

情况1.4.3： $| F_{1} \cup F_{1}^{e} | = 3$

本情况可参考1.3.3的讨论方法，可得 $C W_{4} - F$ 是连通的(矛盾)或 $C W_{4} - F$ 有两个分支，其中一个分支是孤立点。

情况1.4.4： $1 \leq | F_{1} \cup F_{1}^{e} | \leq 2$

由于 $2 \geq | F_{1} \cup F_{1}^{e} | \geq | F_{2} \cup F_{2}^{e} | \geq | F_{3} \cup F_{3}^{e} | \geq | F_{4} \cup F_{4}^{e} | \geq 1$ 。因此，根据命题4(1)、命题6和命题7得， $C W_{4} - F$ 是连通的，矛盾。

情况2： $8 \leq | F | \leq 9$

情况2.1： $| F_{1} | = 6$

情况2.1.1： $6 \leq | F_{1} \cup F_{1}^{e} | \leq 9$

由 $8 \leq | F | \leq 9$ 得， $0 \leq | F_{2} \cup F_{2}^{e} | + | F_{3} \cup F_{3}^{e} | + | F_{4} \cup F_{4}^{e} | + | F_{c} | \leq 3$ ，故 $0 \leq | F_{3} \cup F_{3}^{e} | + | F_{4} \cup F_{4}^{e} | + | F_{c} | \leq 2$ 。根据命题4(1)和命题7得， $C W_{4} [V (C W_{4}^{3} - F_{3} - F_{3}^{e}) \cup V (C W_{4}^{4} - F_{4} - F_{4}^{e})] - F_{c}$ 是连通的。再根据命题5和 $| F_{1} | = 6$ 可以得到 $C W_{4} [V (C W_{4}^{2} - F_{2} - F_{2}^{e}) \cup V (C W_{4}^{3} - F_{3} - F_{3}^{e}) \cup V (C W_{4}^{4} - F_{4} - F_{4}^{e})] - F_{c}$ 是连通的，即 $C W_{4} - F$ 是连通的，矛盾。

情况2.2： $| F_{1} | = 5$

情况2.2.1： $7 \leq | F_{1} \cup F_{1}^{e} | \leq 9$

由于 $7 \leq | F_{1} \cup F_{1}^{e} | \leq 9$ ，故 $0 \leq | F_{2} \cup F_{2}^{e} | + | F_{3} \cup F_{3}^{e} | + | F_{4} \cup F_{4}^{e} | + | F_{c} | \leq 2$ 。根据命题4(1)和命题7得， $C W_{4} [V (C W_{4}^{2} - F_{2} - F_{2}^{e}) \cup V (C W_{4}^{3} - F_{3} - F_{3}^{e}) \cup V (C W_{4}^{4} - F_{4} - F_{4}^{e})] - F_{c}$ 是连通的。再根据命题4(2)和命题5，可以得到 $C W_{4} - F$ 是连通的，矛盾。

情况2.2.2： $| F_{1} \cup F_{1}^{e} | = 6$

在这种情况中， $2 \leq | F_{2} \cup F_{2}^{e} | + | F_{3} \cup F_{3}^{e} | + | F_{4} \cup F_{4}^{e} | + | F_{c} | \leq 3$ 。

如果 $| F_{2} \cup F_{2}^{e} | + | F_{3} \cup F_{3}^{e} | + | F_{4} \cup F_{4}^{e} | + | F_{c} | = 2$ ，根据命题7得， $C W_{4}^{i} - F_{i}$ 是连通的， $i \in [2, 4]$ 。根据命题4(1)，可以得到 $C W_{4} [V (C W_{4}^{2} - F_{2} - F_{2}^{e}) \cup V (C W_{4}^{3} - F_{3} - F_{3}^{e}) \cup V (C W_{4}^{4} - F_{4} - F_{4}^{e})] - F_{c}$ 是连通的。由于 $| F_{c} | \leq 2$ ，根据命题4(2)和命题5，可以得到 $C W_{4} - F$ 是连通的，矛盾。

如果 $| F_{2} \cup F_{2}^{e} | + | F_{3} \cup F_{3}^{e} | + | F_{4} \cup F_{4}^{e} | + | F_{c} | = 3$ 且 $| F_{2} \cup F_{2}^{e} | = 3$ ，则 $| F_{3} \cup F_{3}^{e} | = | F_{4} \cup F_{4}^{e} | = 0$ 且 $| F_{c} | = 0$ 。因此，根据命题4(1)和命题7，有 $C W_{4} [V (C W_{4}^{3} - F_{3} - F_{3}^{e}) \cup V (C W_{4}^{4} - F_{4} - F_{4}^{e})] - F_{c}$ 是连通的。由于 $| F_{c} | = 0$ ，那么根据命题4(2)和命题5，可得 $C W_{4} - F$ 是连通的，矛盾。若 $| F_{i} \cup F_{i}^{e} | \leq 2$ ，其中 $i \in [2, 4]$ 。由命题4(1)、7得， $C W_{4} [V (C W_{4}^{2} - F_{2} - F_{2}^{e}) \cup V (C W_{4}^{3} - F_{3} - F_{3}^{e}) \cup V (C W_{4}^{4} - F_{4} - F_{4}^{e})] - F_{c}$ 是连通的。由于 $| F_{c} | \leq 3$ ，那么 $C W_{4} - F$ 是连通的(矛盾)或 $C W_{4} - F$ 有两个分支，其中一个分支是孤立点。

情况2.2.3： $| F_{1} \cup F_{1}^{e} | = 5$

在这种情况中， $3 \leq | F_{2} \cup F_{2}^{e} | + | F_{3} \cup F_{3}^{e} | + | F_{4} \cup F_{4}^{e} | + | F_{c} | \leq 4$ 。

情况2.2.3.1： $3 \leq | F_{2} \cup F_{2}^{e} | \leq 4$

根据 $8 \leq | F | \leq 9$ ，得 $| F_{3} \cup F_{3}^{e} | + | F_{4} \cup F_{4}^{e} | + | F_{c} | = 0$ 。因此，根据命题4(1)、 $C W_{4}^{i} ≅ B S_{3}$ 和命题7，有 $C W_{4} [V (C W_{4}^{3} - F_{3} - F_{3}^{e}) \cup V (C W_{4}^{4} - F_{4} - F_{4}^{e})] - F_{c}$ 是连通的。由于 $| F_{c} | = 0$ ，那么根据命题4(2)和命题5，可得 $C W_{4} - F$ 是连通的，矛盾。

情况2.2.3.2： $| F_{i} \cup F_{i}^{e} | \leq 2$ ， $i \in [2, 4]$

由命题4(1)和命题7得， $C W_{4} [V (C W_{4}^{2} - F_{2} - F_{2}^{e}) \cup V (C W_{4}^{3} - F_{3} - F_{3}^{e}) \cup V (C W_{4}^{4} - F_{4} - F_{4}^{e})] - F_{c}$ 是连通的。且 $| V (C W_{4}^{1} - F_{1} - F_{1}^{e}) | = 2$ 。由于 $3 \leq | F_{2} \cup F_{2}^{e} | + | F_{3} \cup F_{3}^{e} | + | F_{4} \cup F_{4}^{e} | + | F_{c} | \leq 4$ ，故 $C W_{4} - F$ 是连通的(矛盾)或 $C W_{4} - F$ 有两个分支，其中一个分支是孤立点。

情况2.3： $| F_{1} | = 4$

情况2.3.1： $7 \leq | F_{1} \cup F_{1}^{e} | \leq 9$

同情况2.2.1的讨论方式一样，可得 $C W_{4} - F$ 是连通的，矛盾。

情况2.3.2： $| F_{1} \cup F_{1}^{e} | = 6$

同情况2.2.2的讨论方式一样，可得 $C W_{4} - F$ 是连通的(矛盾)或 $C W_{4} - F$ 有两个分支，其中一个分支是孤立点。

情况2.3.3： $4 \leq | F_{1} \cup F_{1}^{e} | \leq 5$

在这种情况中， $3 \leq | F_{2} \cup F_{2}^{e} | + | F_{3} \cup F_{3}^{e} | + | F_{4} \cup F_{4}^{e} | + | F_{c} | \leq 5$ 。若 $3 \leq | F_{2} \cup F_{2}^{e} | \leq 4$ ，根据 $8 \leq | F | \leq 9$ ，得 $| F_{3} \cup F_{3}^{e} | + | F_{4} \cup F_{4}^{e} | + | F_{c} | \leq 1$ 。根据命题4(1)、 $C W_{4}^{i} ≅ B S_{3}$ 和命题7，我们可以得到 $C W_{4} [V (C W_{4}^{3} - F_{3} - F_{3}^{e}) \cup V (C W_{4}^{4} - F_{4} - F_{4}^{e})] - F_{c}$ 是连通的。再根据命题4(2)和命题5，我们可以得到 $C W_{4} [V (C W_{4}^{2} - F_{2} - F_{2}^{e}) \cup V (C W_{4}^{3} - F_{3} - F_{3}^{e}) \cup V (C W_{4}^{4} - F_{4} - F_{4}^{e})] - F_{c}$ 是连通的。由于 $| F_{c} | \leq 1$ ，故通过命题4(1)、命题4(2)和命题5，我们有 $C W_{4} - F$ 是连通的，矛盾。若 $| F_{i} \cup F_{i}^{e} | \leq 2$ ，其中 $i \in [2, 4]$ 。由命题4(1)、7得， $C W_{4} [V (C W_{4}^{2} - F_{2} - F_{2}^{e}) \cup V (C W_{4}^{3} - F_{3} - F_{3}^{e}) \cup V (C W_{4}^{4} - F_{4} - F_{4}^{e})] - F_{c}$ 是连通的。由于 $3 \leq | F_{c} | \leq 5$ ，那么 $C W_{4} - F$ 是连通的(矛盾)或 $C W_{4} - F$ 有两个分支，其中一个分支是孤立点。

情况2.4： $| F_{1} | = 3$

情况2.4.1： $7 \leq | F_{1} \cup F_{1}^{e} | \leq 9$

同情况2.2.1的讨论方式一样，可得 $C W_{4} - F$ 是连通的，矛盾。

情况2.4.2： $| F_{1} \cup F_{1}^{e} | = 6$

同情况2.2.2的讨论方式一样，可得 $C W_{4} - F$ 是连通的(矛盾)或 $C W_{4} - F$ 有两个分支，其中一个分支是孤立点。

情况2.4.3： $4 \leq | F_{1} \cup F_{1}^{e} | \leq 5$

同情况2.3.3的讨论方式一样，可得 $C W_{4} - F$ 是连通的(矛盾)或 $C W_{4} - F$ 有两个分支，其中一个分支是孤立点。

情况2.4.4： $| F_{1} \cup F_{1}^{e} | = 3$

在这种情况中， $5 \leq | F_{2} \cup F_{2}^{e} | + | F_{3} \cup F_{3}^{e} | + | F_{4} \cup F_{4}^{e} | + | F_{c} | \leq 6$

情况2.4.4.1： $| F_{2} \cup F_{2}^{e} | = 3$

根据 $8 \leq | F | \leq 9$ ，得 $2 \leq | F_{3} \cup F_{3}^{e} | + | F_{4} \cup F_{4}^{e} | + | F_{c} | \leq 3$ 。若 $| F_{3} \cup F_{3}^{e} | = 3$ ，则 $| F_{4} \cup F_{4}^{e} | + | F_{c} | = 0$ 。由 $C W_{4}^{i} ≅ B S_{3}$ 和命题7，得 $C W_{4} [V (C W_{4}^{4} - F_{4} - F_{4}^{e})] - F_{c}$ 是连通的。由于 $3 (n - 2)! > 0 = | F_{c} |$ ，故可得 $C W_{4} [V (C W_{4}^{3} - F_{3} - F_{3}^{e}) \cup V (C W_{4}^{4} - F_{4} - F_{4}^{e})] - F_{c}$ ， $C W_{4} [V (C W_{4}^{2} - F_{2} - F_{2}^{e}) \cup V (C W_{4}^{4} - F_{4} - F_{4}^{e})] - F_{c}$ 是连通的。同理， $C W_{4} [V (C W_{4}^{1} - F_{1} - F_{1}^{e}) \cup V (C W_{4}^{4} - F_{4} - F_{4}^{e})] - F_{c}$ 是连通的，即 $C W_{4} - F$ 是连通的，矛盾。若 $| F_{i} \cup F_{i}^{e} | \leq 2$ ，其中 $i \in [3, 4]$ 。根据命题4(1)、 $C W_{4}^{i} ≅ B S_{3}$ 和命题7，我们可以得到 $C W_{4} [V (C W_{4}^{3} - F_{3} - F_{3}^{e}) \cup V (C W_{4}^{4} - F_{4} - F_{4}^{e})] - F_{c}$ 是连通的。由 $2 \leq | F_{c} | \leq 3$ 和命题4(1)我们可以得到， $C W_{4} [V (C W_{4}^{1} - F_{1} - F_{1}^{e}) \cup V (C W_{4}^{3} - F_{3} - F_{3}^{e}) \cup V (C W_{4}^{4} - F_{4} - F_{4}^{e})] - F_{c}$ ， $C W_{4} [V (C W_{4}^{2} - F_{2} - F_{2}^{e}) \cup V (C W_{4}^{3} - F_{3} - F_{3}^{e}) \cup V (C W_{4}^{4} - F_{4} - F_{4}^{e})] - F_{c}$ 都是连通的。因为 $| F_{j} \cup F_{j}^{e} | = 3$ ， $j \in [1, 2]$ ，所以 $C W_{4}^{1} - F_{1}$ 是连通的或者 $C W_{4}^{1} - F_{1}$ 是三个孤立点。 $C W_{4}^{2} - F_{2}$ 是连通的或者 $C W_{4}^{2} - F_{2}$ 是三个孤立点或者 $C W_{4}^{2} - F_{2}$ 有两个分支，其中一个分支是孤立点。如果 $C W_{4}^{j} - F_{j}$ 是连通的，那么根据命题4(1)，我们有 $C W_{4} - F$ 是连通的，矛盾。如果 $C W_{4}^{1} - F_{1}$ 是三个孤立点且 $C W_{4}^{2} - F_{2}$ 是三个孤立点或者 $C W_{4}^{2} - F_{2}$ 有两个分支，其中一个分支是孤立点，根据 $2 \leq | F_{3} \cup F_{3}^{e} | + | F_{4} \cup F_{4}^{e} | + | F_{c} | \leq 3$ ，则 $C W_{4} - F$ 是连通的(矛盾)或 $C W_{4} - F$ 有两个分支，其中一个分支是孤立点或 $C W_{4} - F$ 有三个分支，其中两个分支是孤立点。如果 $C W_{4}^{1} - F_{1}$ 是连通的， $C W_{4}^{2} - F_{2}$ 是不连通的，那么根据命题4(1)、命题4(2)和命题5以及 $2 \leq | F_{c} | \leq 3$ ，有 $C W_{4} - F$ 是连通的(矛盾)或 $C W_{4} - F$ 有两个分支，其中一个分支是孤立点。

情况2.4.4.2： $| F_{i} \cup F_{i}^{e} | \leq 2$ ， $i \in [2, 4]$

由命题4(1)和命题7得， $C W_{4} [V (C W_{4}^{2} - F_{2} - F_{2}^{e}) \cup V (C W_{4}^{3} - F_{3} - F_{3}^{e}) \cup V (C W_{4}^{4} - F_{4} - F_{4}^{e})] - F_{c}$ 是连通的。因为 $C W_{4}^{i} ≅ B S_{3}$ ，故 $C W_{4}^{1} - F_{1}$ 是连通的或者 $C W_{4}^{1} - F_{1}$ 是三个孤立点。如果 $C W_{4}^{1} - F_{1}$ 是连通的，根据命题4(1)，有 $C W_{4} - F$ 是连通的，矛盾。如果 $C W_{4}^{1} - F_{1}$ 是三个孤立点，且 $5 \leq | F_{c} | \leq 6$ ，那么根据命题4(2)和命题5，可得 $C W_{4} - F$ 有两个分支，其中一个分支是孤立点或者 $C W_{4} - F$ 有三个分支，其中两个分支是孤立点。

情况2.5： $1 \leq | F_{1} | \leq 2$

情况2.5.1： $7 \leq | F_{1} \cup F_{1}^{e} | \leq 9$

同情况2.2.1的讨论方式一样，可得 $C W_{4} - F$ 是连通的，矛盾。

情况2.5.2： $5 \leq | F_{1} \cup F_{1}^{e} | \leq 6$

同情况2.2.2的讨论方式一样，可得 $C W_{4} - F$ 是连通的(矛盾)或 $C W_{4} - F$ 有两个分支，其中一个分支是孤立点。

情况2.5.3： $| F_{1} \cup F_{1}^{e} | = 4$

本情况中，讨论方法类似于情况2.2.3，可得 $C W_{4} - F$ 是连通的(矛盾)或 $C W_{4} - F$ 有两个分支，其中一个分支是孤立点。

情况2.5.4： $| F_{1} \cup F_{1}^{e} | = 3$

本情况的讨论方法类似于情况2.4.4.，可得 $C W_{4} - F$ 是连通的(矛盾)或 $C W_{4} - F$ 有两个分支，其中一个分支是孤立点或者 $C W_{4} - F$ 有三个分支，其中两个分支是孤立点。

情况2.5.5： $1 \leq | F_{1} \cup F_{1}^{e} | \leq 2$

综上可得，本引理结果对于 $n = 4$ 成立。下证当 $n \geq 5$ 时，结果仍成立。

情况1： $| F_{1} \cup F_{1}^{e} | \leq 2 n - 6$

在这种情况中， $| F_{c} | \leq 4 n - 8$ ，且 $| F_{i} \cup F_{i}^{e} | \leq 2 n - 6$ ，其中 $i \in [1, n]$ 。根据定理2.7，对于 $i \in [1, n]$ ， $C W_{n}^{i} - F_{i} - F_{i}^{e}$ 是连通的。根据命题4(1)，可得在任意两个不同的子图 $C W_{n}^{i}^{'} s$ 之间有 $3 (n - 2)!$ 条独立的交叉边。由于 $n \geq 5$ ，故 $3 (n - 2)! > 4 n - 7$ 。因此， $C W_{n} [V (C W_{n}^{i} - F_{i} - F_{i}^{e}) \cup V (C W_{n}^{j} - F_{j} - F_{j}^{e})] - F_{c}$ 是连通的，其中 $i, j \in [1, n]$ ， $i \neq j$ ，即 $C W_{n} - F$ 是连通的，与 $C W_{n} - F$ 是不连通的矛盾。

情况2： $| F_{1} \cup F_{1}^{e} | = 2 n - 5$

情况2.1： $| F_{2} \cup F_{2}^{e} | \leq 2 n - 6$

根据定理2.7，可得对于 $i \in [2, n]$ ， $C W_{n}^{i} - F_{i} - F_{i}^{e}$ 是连通的。因为 $C W_{n}^{1} ≅ B S_{n - 1}$ ，所以根据定理 2.9， $C W_{n}^{1} - F_{1} - F_{1}^{e}$ 是连通的或 $C W_{n}^{i} - F_{i} - F_{i}^{e}$ 有两个分支，其中一个分支是一个孤立点。若 $C W_{n}^{1} - F_{1} - F_{1}^{e}$ 是连通的。因为当 $n \geq 5$ 时，有 $3 (n - 2)! > 4 n - 7$ ，所以根据命题4(1)，我们可以得到 $C W_{n} [V (C W_{n}^{i} - F_{i} - F_{i}^{e}) \cup V (C W_{n}^{j} - F_{j} - F_{j}^{e})] - F_{c}$ 是连通的，其中 $i, j \in [1, n]$ ， $i \neq j$ ，即 $C W_{n} - F$ 是连通的，矛盾。假设 $C W_{n}^{1} - F_{1} - F_{1}^{e}$ 有两个分支，其中一个分支是一个孤立点v。由于 $3 (n - 2)! > 2 n - 2$ ，通过命题4(1)，可得 $C W_{n} [V (C W_{n}^{2} - F_{2} - F_{2}^{e}) \cup V (C W_{n}^{3} - F_{3} - F_{3}^{e}) \cup \dots \cup V (C W_{n}^{n} - F_{n} - F_{n}^{e})] - F_{c}$ 是连通的。因为 $3 ((n - 1)! - (2 n - 5) - 1) > 2 n - 2$ ，其中 $n \geq 5$ ，所以根据命题5，我们可以得到 $C W_{n} [V (C W_{n}^{1} - F_{1} - F_{1}^{e} - v) \cup V (C W_{n}^{2} - F_{2} - F_{2}^{e}) \cup V (C W_{n}^{3} - F_{3} - F_{3}^{e}) \cup \dots \cup V (C W_{n}^{n} - F_{n} - F_{n}^{e})] - F_{c}$ 是连通的。因此， $C W_{n} - F$ 是连通的(矛盾)或 $C W_{n} - F$ 有两个分支，其中一个分支是一个孤立点。

情况2.2： $| F_{2} \cup F_{2}^{e} | = 2 n - 5$

由 $| F_{1} \cup F_{1}^{e} | = 2 n - 5$ 和 $| F | \leq 4 n - 7$ 得， $| F_{i} \cup F_{i}^{e} | \leq 3$ ， $i \in [3, n]$ ， $| F_{c} | \leq 3$ 。因为 $C W_{n}^{i} ≅ B S_{n - 1}$ ，所以根据定理2.7，可得 $C W_{n}^{i} - F_{i} - F_{i}^{e}$ 是连通的。因为 $3 (n - 2)! > 3$ ，所以根据命题4(1)，可以得到 $C W_{n} [V (C W_{n}^{3} - F_{3} - F_{3}^{e}) \cup V (C W_{n}^{4} - F_{4} - F_{4}^{e}) \cup \dots \cup V (C W_{n}^{n} - F_{n} - F_{n}^{e})] - F_{c}$ 是连通的。由定理2.9， $C W_{n}^{j} - F_{j} - F_{j}^{e}$ 是连通的或者 $C W_{n}^{j} - F_{j} - F_{j}^{e}$ 有两个分支，其中一个分支是一个孤立点 $v_{j}$ ， $j \in [1, 2]$ 。假设 $C W_{n}^{j} - F_{j} - F_{j}^{e}$ 是连通的。因为 $3 ((n - 1)! - (2 n - 5)) > 3$ ，所以 $C W_{n} - F$ 是连通的，矛盾。

不失一般性，我们假设 $C W_{n}^{1} - F_{1} - F_{1}^{e}$ 是不连通的， $C W_{n}^{2} - F_{2} - F_{2}^{e}$ 是连通的。因为 $n \geq 5$ ，所以 $3 ((n - 1)! - (2 n - 5) - 1) > 3$ ，所以 $C W_{n} - F$ 是连通的(矛盾)或 $C W_{n} - F$ 有两个分支，其中一个分支是一个孤立点。

若 $C W_{n}^{j} - F_{j} - F_{j}^{e}$ 是不连通的，即 $C W_{n}^{j} - F_{j} - F_{j}^{e}$ 有一个孤立点 $v_{j}$ 。由 $3 ((n - 1)! - (2 n - 5) - 1) > 3$ ，则 $C W_{n} [V (C W_{n}^{1} - F_{1} - F_{1}^{e} - v_{1}) \cup V (C W_{n}^{2} - F_{2} - F_{2}^{e} - v_{2}) \cup V (C W_{n}^{3} - F_{3} - F_{3}^{e}) \cup V (C W_{n}^{4} - F_{4} - F_{4}^{e}) \cup \dots$ $\cup (C W_{n}^{n} - F_{n} - F_{n}^{e})] - F_{c}$ 是连通的。假设 $v_{1}$ 与 $v_{2}$ 相连。那么根据命题4(2)和命题6，可以得到 $| N (v_{j}) \cap (V (C W_{n}^{2}) \cup V (C W_{n}^{3}) \cup \dots \cup V (C W_{n}^{n})) | = 2$ ，通过命题2和 $| F_{i} \cup F_{i}^{e} | \leq 3$ ， $i \in [3, n]$ ， $| F_{c} | \leq 3$ ，所以 $C W_{n} - F$ 是连通的，矛盾。若 $v_{1}$ 与 $v_{2}$ 不相连，则 $C W_{n} - F$ 是连通的(矛盾)或 $C W_{n} - F$ 有两个分支，其中一个分支是一个孤立点或 $C W_{n} - F$ 有三个分支，其中两个分支是孤立点。

情况3： $| F_{1} \cup F_{1}^{e} | = 2 n - 4$

本情况的讨论方法类似于情况2，可得 $C W_{n} - F$ 是连通的(矛盾)或 $C W_{n} - F$ 有两个分支，其中一个分支是一个孤立点或 $C W_{n} - F$ 有三个分支，其中两个分支是孤立点。

情况4： $2 n - 3 \leq | F_{1} \cup F_{1}^{e} | \leq 4 n - 13$

情况4.1： $2 n - 5 \leq | F_{2} \cup F_{2}^{e} | \leq 2 n - 4$

根据 $| F | \leq 4 n - 7$ ，得 $| F_{3} \cup F_{3}^{e} | + | F_{4} \cup F_{4}^{e} | + \dots + | F_{n} \cup F_{n}^{e} | \leq 1$ ， $| F_{c} | \leq 1$ ，所以根据命题4(1)， $C W_{n} [V (C W_{n}^{3} - F_{3} - F_{3}^{e}) \cup V (C W_{n}^{4} - F_{4} - F_{4}^{e}) \cup \dots \cup V (C W_{n}^{n} - F_{n} - F_{n}^{e})] - F_{c}$ 是连通的。因为 $n \geq 5$ ，所以 $3 (n - 2)! > 4 n - 7$ ，所以 $C W_{n} [V (C W_{n}^{1} - F_{1} - F_{1}^{e}) \cup V (C W_{n}^{3} - F_{3} - F_{3}^{e}) \cup \dots \cup V (C W_{n}^{n} - F_{n} - F_{n}^{e})] - F_{c}$ 是连通的， $C W_{n} [V (C W_{n}^{2} - F_{2} - F_{2}^{e}) \cup V (C W_{n}^{3} - F_{3} - F_{3}^{e}) \cup \dots \cup V (C W_{n}^{n} - F_{n} - F_{n}^{e})] - F_{c}$ 是连通的，即 $C W_{n} - F$ 是连通的，矛盾。

情况4.2： $| F_{2} \cup F_{2}^{e} | \leq 2 n - 6$

根据定理2.7，可得对于 $i \in [2, n]$ ， $C W_{n}^{i} - F_{i} - F_{i}^{e}$ 是连通的。因为 $n \geq 5$ ， $3 (n - 2)! > 4 n - 7$ ，所以根据命题4(1)，有 $C W_{n} [V (C W_{n}^{2} - F_{2} - F_{2}^{e}) \cup V (C W_{n}^{3} - F_{3} - F_{3}^{e}) \cup \dots \cup V (C W_{n}^{n} - F_{n} - F_{n}^{e})] - F_{c}$ 是连通的。根据命题10，可得 $C W_{n}^{1} - F_{1} - F_{1}^{e}$ 是连通的或者 $C W_{n}^{1} - F_{1} - F_{1}^{e}$ 有两个分支，其中一个分支是孤立点或 $C W_{n}^{1} - F_{1} - F_{1}^{e}$ 有三个分支，其中两个分支是孤立点。假设 $C W_{n}^{1} - F_{1} - F_{1}^{e}$ 是连通的。因为 $n \geq 5$ ，所以 $3 ((n - 1)! - (4 n - 13)) > 2 n - 4$ 。因此， $C W_{n} - F$ 是连通的，矛盾。假设 $C W_{n}^{1} - F_{1} - F_{1}^{e}$ 有两个分支，其中一个分支是孤立点。因为 $3 ((n - 1)! - (4 n - 13) - 1) > 2 n - 4$ ，其中 $n \geq 5$ ，所以 $C W_{n} - F$ 是连通的(矛盾)或 $C W_{n} - F$ 有两个分支，其中一个分支是孤立点。假设 $C W_{n}^{1} - F_{1} - F_{1}^{e}$ 有三个分支，其中两个分支是孤立点。因为当 $n \geq 5$ 时，有 $3 ((n - 1)! - (4 n - 13) - 2) > 2 n - 4$ ，所以 $C W_{n} - F$ 是连通的(矛盾)或 $C W_{n} - F$ 有两个分支，其中一个分支是一个孤立点或 $C W_{n} - F$ 有三个分支，其中两个分支是孤立点。

情况5： $4 n - 12 \leq | F_{1} \cup F_{1}^{e} | \leq 4 n - 7$

在这种情况中， $| F_{2} \cup F_{2}^{e} | + | F_{3} \cup F_{3}^{e} | + \dots + | F_{n} \cup F_{n}^{e} | + | F_{c} | \leq 5$ 。当 $n \geq 5$ ， $3 (n - 2)! > 5$ ，故由命题4(1)和定理2.7，有 $C W_{n} [V (C W_{n}^{3} - F_{3} - F_{3}^{e}) \cup V (C W_{n}^{4} - F_{4} - F_{4}^{e}) \cup \dots \cup V (C W_{n}^{n} - F_{n} - F_{n}^{e})] - F_{c}$ 是连通的。因为 $| F_{c} | \leq 5$ ， $C W_{n} [V (C W_{n}^{2} - F_{2} - F_{2}^{e}) \cup V (C W_{n}^{3} - F_{3} - F_{3}^{e}) \cup \dots \cup V (C W_{n}^{n} - F_{n} - F_{n}^{e})] - F_{c}$ 是连通的。若 $C W_{n}^{1} - F_{1} - F_{1}^{e}$ 是连通的，则根据命题4(1)，我们可以得到 $C W_{n} - F$ 是连通的，矛盾。若 $C W_{n}^{1} - F_{1} - F_{1}^{e}$ 是不连通的。由命题4(1)和命题4(2)以及 $| F_{2} \cup F_{2}^{e} | + | F_{3} \cup F_{3}^{e} | + \dots + | F_{n} \cup F_{n}^{e} | \leq 5$ 和 $| F_{c} | \leq 5$ ，可得 $C W_{n} - F$ 是连通的(矛盾)或 $C W_{n} - F$ 有两个分支，其中一个分支是一个孤立点。

定理4.6 对于任何整数 $n \geq 4$ ， $n κ λ (C W_{n}) = 4 n - 6$ 。

证明：令F是 $C W_{n}$ 的一个最小强自然割。那么根据引理4.5， $| F | \geq 4 n - 6$ 。令 $u = (1)$ ， $v = (12)$ ，并且令 $F = {u x : x \in {(1, i) : 3 \leq i \leq n} \cup {(i, i + 1) : 2 \leq i \leq n - 1} \cup {(2, n)} \cup {(12) (1, i) : 3 \leq i \leq n} \cup$ ${(12) (i, i + 1) : 2 \leq i \leq n - 1} \cup {(12) (2, n)}$ 。由命题2得， $C W_{n}$ 没有奇圈。因此，对于任意的 $x \in (C W_{n} - F)$ ， $d_{C W_{n}} (x) \geq 2 n - 2 - (2 n - 3) \geq 1$ 。因此，我们可以得到F是 $C W_{n}$ 的一个自然割，所以， $n κ λ (C W_{n}) \leq 4 n - 6$ 。结合 $| F | \geq 4 n - 6$ ，我们有 $n κ λ (C W_{n}) = 4 n - 6$ 。

5. 结论

本文研究了n维轮图 $C W_{n}$ 当 $g = 0$ 、 $g = 1$ 的强连通性质，得到了当 $g = 0$ 时，对于任何整数 $n \geq 4$ ， $κ λ (C W_{n}) = 2 n - 2$ 。进一步，在条件加强的基础上，即当 $g = 1$ 时，得到了 $n κ λ (C W_{n}) = 4 n - 6$ 。由于本文没有对 $g \geq 2$ 进行研究，因此这将是一个今后很有研究价值的课题。

致谢

本论文是在我的导师王世英教授的悉心指导下完成的。他渊博的专业知识，严谨的治学态度，精益求精的工作作风，诲人不倦的高尚师德，严于律己、严以律己、宽以待人的崇高风范，朴实无华、平易近人的人格魅力对本人影响深远。不仅使本人树立了远大的学习目标，掌握了基本的研究方法，还使本人明白了许多为人处事的道理。本次论文从选题到完成，每一步都倾注了导师大量的心血。在写论文的过程中，遇到了很多的问题，在王老师的耐心指导下，问题都得以解决。在此，谨向王老师表示崇高的敬意和衷心的感谢！

还要感谢我同小组的赵丽娜师姐和两位同门，是你们在平时论文中和我一起探讨问题，并指出我论文上的误区，使我能及时地发现问题把论文顺利的进行下去，没有你们的帮忙我不可能这样顺利地结稿，在此表示深深的谢意。

基金项目

国家自然科学基金资助项目(61772010)，山西省基础研究计划(202203021221128)。

文章引用

王苏,王世英. 轮图的强连通性
The Strong Connectivity of the Wheel Network[J]. 应用数学进展, 2023, 12(06): 3039-3054. https://doi.org/10.12677/AAM.2023.126305

参考文献

1. Bondy, J.A. and Murty, U.S.R. (2008) Graph Theory. Springer, New York.

2. Wei, F. and Wang, S. (2021) Struc-ture Connectivity and Substructure Connectivity of Wheel Networks. Theoretical Computer Science, 850, 20-29. https://doi.org/10.1016/j.tcs.2020.10.028

3. Wang, S. and Wang, M. (2019) The Strong Connectivity of Bub-ble-Sort Star Graphs. The Computer Journal, 62, 715-729. https://doi.org/10.1093/comjnl/bxy077

4. Guo, J. and Lu, M. (2021) Edge-Fault-Tolerant Strong Menger Edge Connectivity of Bubble-Sort Star Graphs. Discrete Applied Mathematics, 297, 109-119. https://doi.org/10.1016/j.dam.2021.03.006

5. Wang, S., Wang, Z. and Wang, M. (2016) The 2-Extra Connectivity and 2-Extra Diagnosability of Bubble-Sort Star Graph Networks. The Computer Jour-nal, 59, 1839-1856. https://doi.org/10.1093/comjnl/bxw037

6. Hou, F. (2013) Some New Results of the Wheel Networks and Bubble-Sort Star Networks. Master’s Thesis, Northwest Normal University, Lanzhou. (In Chi-nese)

7. Feng, W., Ren, J. and Wang, S. (2019) The Nature Diagnosability of Wheel Graph Networks Under the PMC Model and MM Model. Ars Combinatoria, 143, 255-287.

8. Feng, W., Ren, J., Enhe, C. and Wang, S. (2020) The 2-Good-Neighbor Connectivity of Wheel Graph Networks. Utilitas Mathematica Journal, 116, 139-167.

9. Cai, H., Liu, H. and Lu, M. (2015) Fault-Tolerant Maximal Local-Connectivity on Bubble-Sort Star Graphs. Discrete Applied Mathematics, 181, 33-40. https://doi.org/10.1016/j.dam.2014.10.006

10. Gu, M., Hao, R., Tang, S. and Chang, J. (2019) Analysis on Component Connectivity of Bubble-Sort Star Graphs and Burnt Pancake Graphs. Discrete Applied Mathematics, 279, 80-91. https://doi.org/10.1016/j.dam.2019.10.018

11. Wang, S., Wang, Z. and Wang, M. (2017) The 2-Good-Neighbor Connectivity and 2-Good-Neighbor Diagnosability of Bubble-Sort Star Graph Networks. Dis-crete Applied Mathematics, 217, 691-706. https://doi.org/10.1016/j.dam.2016.09.047

12. Feng, W. and Wang, S. (2020) The Diagnosability of Wheel Net-works with Missing Edges under the Comparison Model. Mathematics, 8, Article 1818. https://doi.org/10.3390/math8101818

13. Feng, W. and Wang, S. (2020) The 2-Extra Connectivity of Wheel Net-works. Mathematical Problems in Engineering, 2020, Article ID: 8910240. https://doi.org/10.1155/2020/8910240

14. Guo, J. and Lu, M. (2016) Conditional Diagnosability of Bubble-Sort Star Graphs. Discrete Applied Mathematics, 201, 141-149. https://doi.org/10.1016/j.dam.2015.07.026

15. Wang, M., Yang, W., Guo, Y. and Wang, S. (2016) Conditional Fault Tolerance in a Class of Cayley Graphs. International Journal of Computer Mathematics, 3, 67-82. https://doi.org/10.1080/00207160.2014.988615

16. He, S.J., Hao, R.X. and Cheng, E. (2018) Strongly Menger-Edge-Connectedness and Strongly Menger-Vertex- Connectedness of Reg-ular Networks. Theoretical Computer Science, 731, 50-67. https://doi.org/10.1016/j.tcs.2018.04.001

17. Wang, Y. and Wang, S. (2021) Edge-Fault-Tolerant Strong Menger Edge Connectivity of Bubble-Sort Graphs. AIMS Mathematics, 6, 13210-13221. https://doi.org/10.3934/math.2021763

18. Zhou, S. and Chen, L. (2010) Fault Tolerant Maximal Local Connectiv-ity of Alternating Group Networks. Proceedings of 2010 3rd International Congress on Image and Signal Processing, Yantai, 16-18 October 2010, 4394-4398. https://doi.org/10.1109/CISP.2010.5648134

期刊菜单