Advances in Education
Vol.
13
No.
09
(
2023
), Article ID:
71844
,
5
pages
10.12677/AE.2023.1391008
应用数理统计课程融入R软件的教学实践研究
黄彬
北京化工大学数理学院,北京
收稿日期:2023年8月2日;录用日期:2023年8月30日;发布日期:2023年9月6日

摘要
本文以正态性检验和回归分析为例,介绍了R软件在应用数理统计课程教学实践中的应用。课程教学融合统计软件和案例分析,这有助于加深学生对统计学理论知识的直观理解,激发学生的学习兴趣,提高学生数据分析实践能力。
关键词
应用数理统计,R软件,数据分析,实践能力

Research on Teaching Practice of Applied Mathematical Statistics by Using R Software
Bin Huang
School of Mathematics and Physics, Beijing University of Chemical Technology, Beijing
Received: Aug. 2nd, 2023; accepted: Aug. 30th, 2023; published: Sep. 6th, 2023

ABSTRACT
By taking normality test and regression analysis as examples, this paper mainly discusses the teaching practice of applied mathematical statistics by using R software. Software-assisted teaching through case study will help students to deepen their intuitive understanding of basic theory of statistics, stimulate their interest in learning, and ultimately improve their practical ability of data analysis.
Keywords:Applied Mathematical Statistics, R Software, Data Analysis, Practical Ability

Copyright © 2023 by author(s) and Hans Publishers Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY 4.0).
http://creativecommons.org/licenses/by/4.0/


1. 引言
应用数理统计是高等院校理工科、经管等相关专业研究生的一门公共基础课,教学内容涵盖参数估计、假设检验、方差分析、回归分析等统计方法,是一门实用性非常强的统计学科。在课程教学和实际应用中,经常会遇到复杂的公式推导和繁琐的统计计算,这都不可避免要使用统计软件。因此,在教学中注重实践环节,借助统计软件辅助教学,将理论知识和实际相结合,不仅可以将一些抽象难懂的内容可视化,提高学生的学习兴趣,还有助于提高学生的统计计算能力和解决实际问题的能力 [1] [2] 。
常用的统计软件有R、SAS、SPSS、Stata、Matlab等,他们的计算功能大同小异,各有优劣。其中R软件因其强大的统计计算、数据分析和绘图功能,吸引了越来越多的使用者。而且,R软件是免费开源的,它入门简单,扩展性强,有很多软件包可供使用,应用范围广泛。因此,在教学过程中,使用R软件进行辅助教学是非常好的一种选择。针对数理统计类课程的教学内容和特点,文献 [3] [4] [5] [6] [7] 介绍了R软件在课程教学中的应用优势和延伸功能,论证了R软件对实践教学的支撑作用。
结合本校的教学实践,以案例教学为例,本文将研究如何把R软件融入到应用数理统计课程中,利用R软件的计算和绘图功能展示统计方法的基本理论和计算过程,为课程教学改革提供具体思路。利用R软件辅助教学可以帮助学生加深对统计学理论知识的直观理解,提高学生的软件操作能力和统计计算能力,促进学以致用。
2. R软件在教学中的应用案例
本节通过几个案例来介绍如何在应用数理统计教学中使用R软件进行一些统计计算和案例分析。
2.1. 正态性检验
在数据分析中,经常需要判断数据是否服从正态分布。可通过画图和非参数检验方法相结合展示正态性检验的基本步骤。我们以84个伊特鲁利亚人(Etruscans)男子头颅的最大宽度(以mm计)的数据为例,先通过画概率直方图和QQ图的方式做初略的判断,观察数据分布的特征。
> data=read.table(width.txt,header=T) ##读取数据
> width=data$width; n=length(width)
> summary(width)##获取描述性统计量
从描述性分析的结果可以得到数据的最大值、最小值、中位数、均值、上下四分位数等信息。
> par(mfrow=c(1,2))
> hist(width,breaks=6,freq=FALSE,xlab=width,ylab=频数密度,main=直方图)
> lines(density(width)) #直方图和密度函数曲线的叠加
> qqnorm(width,main=Q-Q图); qqline(width) # QQ图
> par(mfrow=c(1,1))
从图1可以初略判断,该数据呈现正态分布的特征。更精确的正态性检验方法是非参数检验,常用的方法如:Pearson卡方检验,Shapiro-Wilk检验、K-S检验、Cramer-von Mises检验等。
## Pearson卡方检验
> br=c(-Inf,134.5,138.5,142.5,146.5,150.5, Inf)
> a=table(cut(width,breaks = br))#把数据分成6组,统计每组的频数
> a=as.data.frame(a); freq=a$Freq
> p=pnorm(br, mean(width), sd(width))
> K=length(br)-1; r=2
> p.hat=diff(p)#落在每组的概率
> chi=sum((freq-n*p.hat)^2/(n*p.hat))#Pearson统计量的值
> p.value=1-pchisq(chi, K-r-1)
> cat(chisq=, chidf=, K-r-1p-value=, p.value)

Figure 1. Histogram and QQ plot
图1. 直方图和Q-Q图
结果显示,Pearson卡方检验的p值为0.477 > 0.05,故可认为该数据来自正态分布总体。这里要注意,Pearson卡方检验的结果依赖于分组情况。还可利用Shapiro-Wilk检验、K-S检验、Cramer-von Mises检验等方法检验正态性。
> shapiro.test(width)
> library(nortest)
> lillie.test(width) #K-S检验
> cvm.test(width) #Cramer-von Mises检验
这3种检验方法的p值分别为0.689,0.132,0.395,均支持该数据来自正态分布总体的论断。
2.2. 线性回归
回归分析是研究变量间相关性的一种统计分析方法。“回归分析”这一词的由来要追溯到英语遗传学家F. Galton的一项工作,根据他的研究发现:儿子的身高受到父亲身高的影响,但儿子身高有回归到子代平均身高的趋势。我们以UsingR包中的数据father.son为例,利用R软件对其进行回归分析,验证Galton的论断。
> library(UsingR)
> data(father.son)
> n=length(x); x=father.son$fheight; y=father.son$sheight
> plot(x,y,xlab=父身高,ylab=子身高) #画散点图
> abline(lm(y~x)) #添加回归直线
> fit.lm=lm(y~x) #拟合模型
> summary(fit.lm)#输出结果
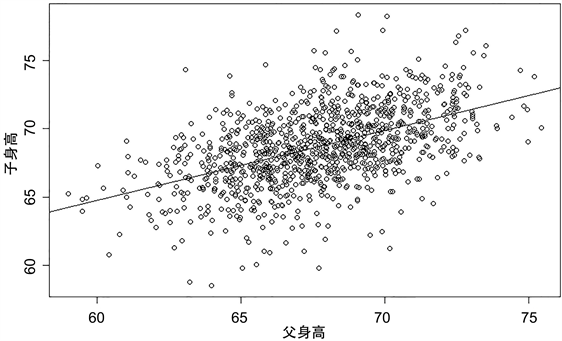
Figure 2. Scatter plot
图2. 散点图
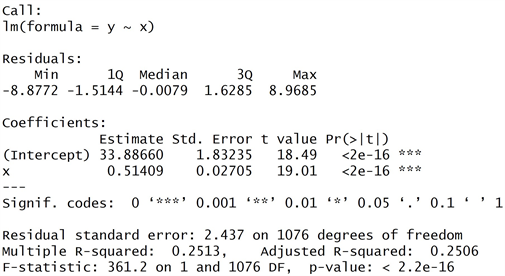
Figure 3. Running results
图3. 运行结果
从图2中可以看出,儿子身高y与父亲身高x具有比较明显的线性相关关系,因此可用线性回归模型来拟合它们的关系。使用函数summary()显示拟合的结果(见图3),回归方程可表示为
(单位:英寸)
这表明父亲身高每增加l英寸,儿子身高增加0.514英寸。且回归方程的显著性检验(F检验)的p值为 ,可见回归效果高度显著,即:儿子身高与父亲身高有密切的线性关系。
另外,为了验证“儿子身高有回归到子代平均身高的趋势”这一论断,需要对线性回归模型的回归系数(斜率项) 进行检验,即检验 。其R代码如下:
> X=cbind(1,x);
> beta=solve(t(X)%*%X)%*%t(X)%*%y;beta1=beta[2]
> RSS=t(y)%*%y-t(beta)%*%t(X)%*%y#残差平方和
> sigma=sqrt(RSS/(n-2))
> Sxx=sum(x^2)-sum(x)^2/n
> T=(beta1-1)*sqrt(Sxx)/sigma#检验统计量的值
> p.value=pt(T,n-2)#检验的p值
该t检验的p值为 ,故可拒绝 ,即认为 ,从而Galton的断言得到证实。
最后还可利用回归方程进行预测,通过运行如下R代码:
> predict(fit.lm,data.frame(x=71.2),interval=prediction,level=0.95)
> predict(fit.lm,data.frame(x=71.2),interval=confidence,level=0.95)
得出,若父亲的身高为71.2英寸,则可预测一个儿子的身高值为70.49英寸及95%的预测区间:(65.70, 75.28),还可预测儿子的平均身高值为70.49英寸及95%的置信区间:(70.25, 70.73)。
3. 结论
从几个应用案例可以看到,将R软件引入课程教学中,可用几行简单的代码实现复杂的统计计算,这有利于让学生摆脱繁琐的计算和公式推导,还能把抽象的理论知识直观化和具体化,加深学生对理论知识的直观理解,激发学生的学习兴趣。应用数理统计是一门实用性非常强的学科,在教学活动中,应以培养学生数据思维能力和创新实践能力为目标。因此,案例教学在统计软件的有效支撑下,将理论知识、软件应用与统计建模三者融为一体,有利于将理论知识和实际相结合,更大程度地提高学生统计软件的应用能力和数据分析实践能力,从而促进学以致用,提升教学质量,增强教学效果。
基金项目
北京化工大学2021年研究生教育教学改革项目(G-JG-PTKC202113, G-JG-PTZG202110);北京化工大学2022年数理学院本科教学教改项目。
文章引用
黄 彬. 应用数理统计课程融入R软件的教学实践研究
Research on Teaching Practice of Applied Mathematical Statistics by Using R Software[J]. 教育进展, 2023, 13(09): 6474-6478. https://doi.org/10.12677/AE.2023.1391008
参考文献
- 1. 周晓东, 王云娟. 基于统计软件的统计学教学研究与实践[J]. 大学教育, 2018(7): 45-48.
- 2. 黄彬. 基于研究生数据分析能力培养的应用数理统计课程教学改革探究[J]. 吉林化工学院学报, 2021, 38(6): 1-4.
- 3. 崔玉杰, 刘喜波. R和Python软件在《概率论与数理统计》教学中应用初探[J]. 教育教学论坛, 2017(12): 192-193.
- 4. 赵为华. R软件在概率论与数理统计案例教学中的应用[J]. 福建电脑, 2018, 34(5): 171-172.
- 5. 宋述芳, 迟乃荣, 吕震宙. R语言在数理统计教学中的应用及延伸[J]. 教育教学论坛, 2019(9): 231-233.
- 6. 李静, 李雪艳, 魏传华. 基于R软件“概率论与数理统计”课程的教学改革初探[J]. 教育进展, 2022, 12(12): 5690-5693. https://doi.org/10.12677/AE.2022.1212866
- 7. 徐锋, 蒋远营. 大数据时代统计学类专业教学中的R语言应用研究[J]. 高教学刊, 2022(13): 10-13.