 Applied Physics 应用物理, 2012, 2, 7-13 http://dx.doi.org/10.12677/app.2012.21002 Published Online January 2012 (http://www.hanspub.org/journal/app) The Stability of Density Stratified Liquid Film Flowing Down a Linear Heated Inclined Plate* Xiaochao Fan College of Electrical Engineering, Xinjiang University, Urumqi Email: fxc0102@126.com Received: Nov. 21st, 2011; revised: Dec. 20th, 2011; accepted: Dec. 22nd, 2011 Abstract: The flow and heat transfer in stratified liquid film falling down a linear heated inclined plate are described by the N-S equations, and the corresponding mathematical models are established. Then the governing equations and their boundary conditions of the small perturbation are derived. The equations are solved by the perturbation method, and then the expression of dispersion relation is obtained and analyzed. At last the effects of different factors on the stability of the film are discussed using numerical simulation. The stratification effect is not obvious, the liquid flow is stable. And the liquid film flow is instability because of linear heating. Keywords: Density Stratified Liquid Film; Linear Heated Plate; Perturbation Method; Flew and Heat; Stability Analysis 密度分层液膜沿线性加热斜面流动稳定性* 樊小朝 新疆大学电气工程学院,乌鲁木齐 Email: fxc0102@126.com 收稿日期:2011年11月21日;修回日期:2011 年12 月20 日;录用日期:2011 年12 月22日 摘 要:由N-S 方程及合理的边界条件对沿线性加热斜面下降的密度分层液膜流动和传热问题进行描述,建立 数学模型。进一步推导出液膜中小扰动满足的控制方程和边界条件。用摄动法进行求解,得到色散关系的表达 式,并对其进行分析。数值模拟不同因素对液膜稳定性的影响,得到分层效应不明显液膜流动越稳定,线性加 热对液膜流动起失稳作用。 关键词:密度分层液膜;线性加热平板;摄动法;流动传热;稳定性分析 1. 引言 薄液膜流动是工程热物理及流体力学等领域具 有重要研究意义的课题。自由下降液膜以其具有小流 量、小温差、高换热系数、高热流密度、结构简单、 动力消耗小等独特优点而成为一项高效传热传质技 术。与波状液膜沿倾斜平板流动有关的问题的研究十 分活跃[1-3]。薄液膜的贴壁流动具有很强的热交换能 力,因而在化工、核能、动力、制冷等领域得到广泛 的应用,如蒸汽透平叶片、航空发动机和微电子芯片 等元件的冷却,都存在着线性或非线性流动换热,在 一些传热设备的设计上,比如电厂中换热器、蒸发器、 冷凝器和热管也有重要作用[4-6]。 分层流是指密度(不可压缩流体)或熵(可压缩流 体)等非均匀的流体运动[7,8]。在现实情况中,液体液 膜不一定都是密度均匀的,也可能存在两层或多层流 体平行流动的情况,所以对于密度分层液膜的流动传 *基金项目:国家自然科学基金资助项目(51106132):分层液膜沿非 均匀受热斜面流动传热特性分析。 Copyright © 2012 Hanspub 7  密度分层液膜沿线性加热斜面流动稳定性 热稳定性研究也同样具有重要的实际意义。 关于分层薄膜流动及其稳定性的研究,Kao[9,10] 对沿平板下落的两层液膜进行了线性稳定性分析, Weinstein 和Kurz[11]对沿平板下落的三层液膜进行了 长波不稳定性研究,Loewenherz[12]和Chen[13]分别研 究了在小雷诺数情况下分层液膜流动的表面不稳定 性和表面波的形成。李欣[14]从分层流理论出发,建立 了带有粘性项的一般密度分层液膜小振幅内波和非 线性内波的流动模型,讨论了表征流动稳定性的特征 参数,并推导出在浅水假定下分层液膜流动中较一般 的非线性内波控制方程及其边界条件。田英[15]用N-S 方程和合理的边界条件对沿加热壁面下降的分层液 膜的流动和传热问题进行了数学描述,推导出分层液 膜中小扰动满足的控制方程和边界条件,对一定的液 膜密度分布进行了稳定性分析,数值模拟了不同因素 对分层液膜稳定性的影响。对加热液膜流动稳定性的 研究,印度Arghya Samanta[16]研究了非惯性液膜沿均 匀加热斜面下滑的稳定性,他用正则模法分析研究了 下降液膜的线性稳定性,又研究了液膜沿垂直的非均 匀加热斜面流动稳定性[17],假定壁面温度是线性变化 的,并利用长波摄动法得到非线性演化方程,用多尺 度方法进行了非线性稳定分析,研究了行波解的演化 方程,结果表明随着 Peclet 数的增加超临界不稳定区 域将会增加。 经调研,以前对液膜的研究有非分层液膜沿加热 平板流动,也有密度分层液膜沿恒温平板流动,将两 者结合起来没人研究过[18]。因此,本文对密度分层液 膜沿线性加热斜面流动进行研究。 2. 液膜流动模型 考虑分层液体薄膜在重力作用下沿底部加热的 倾斜平板下落,液膜垂直平均厚度为 d,平板与水平 夹角为 β,设自由面方程为 , y hxt,并且假设周围 的环境为无粘和静止的气体温度为T0,平板上的温度 分布为 ,其 中 10 TTxT 0 – m TT T,Tm为非均匀 加热平板上的最大温度,如图1。 在该坐标系下液膜流动的控制方程及边界条件, 无量纲化的控制方程为: 0 xy uv (1) 22 txyx Re uuuvupu (2) y 0 T 0 T 1 g x d β ρ(y) Figure 1. Diagram of stratified liquid flows along the heated slope 图1. 密度分层液膜沿加热斜面流动示意图 22cot txy y Re vuvvvpv (3) txy PrReu v (4) 以及边界条件: 0 uv y0 (5) 20 1 yx x uv My 1 (6) 0 yxx vpWe y (7) 01 tx hu vy (8) 0xy (9) 0 1 Bi y n (10) 下标表示求导,式中雷诺数 0 Reu d ,弗罗德 数22 0 F rugd,Weber 数2 00 sinWe gd ,Biot 数Bid k ,普朗特数 Pr ,Marangoni 数 Ma Td ,Ma ,Pr ,Re 之间的关系可用 2 M Ma PrRe 表示,法向 , ,1 x n , x y 。其中 u 、 v分别为水平、垂直方向的速 度,p0为环境压强, 为放热系数,k为导热系数,ν 为运动粘性系数,μ为动力粘性系数,κ为热扩散系 数。 为表面张力系数,与温度的关系式为: 0 TTT 0 T (11) 其中系数 γT 。 无量纲温度 0m TT TT 0 ,特征速度、时 间、压强和密度分别为: 2 0sinugd2 ,0 ud, 0singd ,0 。 假设 0Bi ,其物理意义:流体表面是绝热的, 这与长波演化方程的推导前提是一致的。下面对上述 无量纲方程进行小扰动展开和正则模求解,设 uuu ,vv ,ppp , , ,1h (12) 当0Bi ,1 时,存在基本流场: 8 Copyright © 2012 Hanspub  密度分层液膜沿线性加热斜面流动稳定性 Copyright © 2012 Hanspub 9 2 34 21 1cot 2 1312 3 uMyy py yy x PrReMPrReM y (13) 这一结果和文献[19]是一致的。 当密度 y e 在小参数 下展开为 1 y 时, 代表密度分层效果[18],可以得到基本流场为式(14)。 用 23 2 34 5 2 21 3 1 cot 11 2 12 13123036 uMyyy pyy yy 5 x PrReMy PrReMy (14) 由正则模方法,设 假设液膜不可压缩且非扩散,则有 ,,, ,,, ikx tikx t xytfyepxythye d0 dt (17) ,,, , ikx tikx t xytg yexte (15) 此式线性化后为: 其中 f,h,g,ξ分别为流函数、压力、温度、表 面波动沿 y向的无量纲幅值,在本文中ξ扰动的初始 值为一很小的量。2πk 为无量纲波数,λ为波长。 ω为角频率, r ii 。角频率与相速度的关系: c d0 d uv txy (18) 设 和 具有相同的指数因子,由上式得 k 。并且相速度 为扰动的无量纲复速 度,cr表示波动传播的速度,ci代表激励量,i为虚数 单位。 r ic i cc ikx t kfe ku w (19) 将扰动量代入,在代入过程中消去了压强项,最 后得到分层线性加热液膜的线性稳定性控制方程及 其边界条件为式(20),(21),(22(a-d)): 速度势函数有如下关系: uy ,vx (16) 424 2 22 2cot ik fu f kf kffff uc ucuc ikRe ucffkfuuf (20) 2 y gkgikPrReucgf f (21) 21 112 1 yy u fk fikMg cu 10 (22b) 00, 00ff (22a) 3 3 2 2141 2 1111111 1 yy y yy ikWepik p ik We fikReucf kWeikReuf uc ucu 0 (22c) 1 00 ,11221 f ggPrReMik uc 0 (22d) 方程(19)就是 O-S(Orr-Sommerfeld)方程,下面对 其进行求解。当密度为常数(1 )时,上面的方程和 文献[20]得到的方程是一致的。 3. 控制方程的求解 由于波长越长,扰动越不易衰减,流动越易趋向 不稳定,因此,分析液膜流动稳定性时,只需了解长 波扰动的增减趋势,即考察无量纲波数为零阶和一阶 小量的情况,设 22 010 1 ,ffkfOkg gkgOk 2 01 cckc Ok (23)  密度分层液膜沿线性加热斜面流动稳定性 其中“0”和“l”分别表示零阶和一阶小量的情 况, k为2π 一个无穷小量。将上面的式子带入方程 (20)至(22)中,在微分方程组中保留k的线性项,略去 二次以上的项。比较常数项,得 4 0 00 00 0 0 0 0 0 0 00, 00, 2 1 12 (1)0 00 112 f fRePr g ff f Mc f g gRePrM 0 1 0 f (24) 求解可以得到: 23 00 1 , 32 f y gPrReyMay (25) 比较 k的一次幂系数,得式(26) 4 1 11 111 2 1 41 1 00, 00, 20281 121222 0 333 14 1212 12cot10 33 fiReMy ff ffciMPrReM fiReiReMiRekWe a (26) 最后可以得到色散关系式(27),(28): 01 21cc kcMkc 1 (27) 2 2 1 2 2 8215 4 cot 15 32615 142 177 1410cot 31553 Ma Ma ci RekWeMa PrRe Pr iMa Ma ReMakWe PrRe Pr (28) 当0 时,得到色散关系式(29)。 2 2 1 8215 4 cot 15 32615 M a ci RekWeMa PrRe Pr Ma (29) 此结果与文献[20]得到的色散关系是一样的。 在式(27)中,实部代表在液膜内的传播速度 u0, 虚部表示扰动随时间的变化规律,当小于零时,扰动 将衰减或保持不变,流动保持稳定,当大于零时,扰 动随时间增长,流动将趋于失稳。Re代表惯性力和粘 性力的影响,We 代表表面张力的影响,Ma数是反映 表面张力梯度的参数,Fr 代表热对流和热传导的影 响, 代表密度分层的影响。 4. 数值模拟及稳定性分析 波数 k为实数,角频率 ω为复数,反映的扰动在 空间上是周期性的,其幅值随时间演化,称为时间模 式。当 ωi > 0 时,扰动模态是不稳定的;当 ωi = 0 时, 扰动模态是中性稳定的;当ωi < 0时,扰动模态是稳 定的在时间模式下,用 MATLAB 进行数值模拟,讨论 Re 数、Marangoni 数、We 数、角度、Pr 数以及分层 效应对流动稳定性的影响。 4.1. Re 数的影响 当ε = 0,k = 0,Ma = 0 时,利用(28)式可以得到 临界雷诺数为: 54cot c Re (30) 10 Copyright © 2012 Hanspub 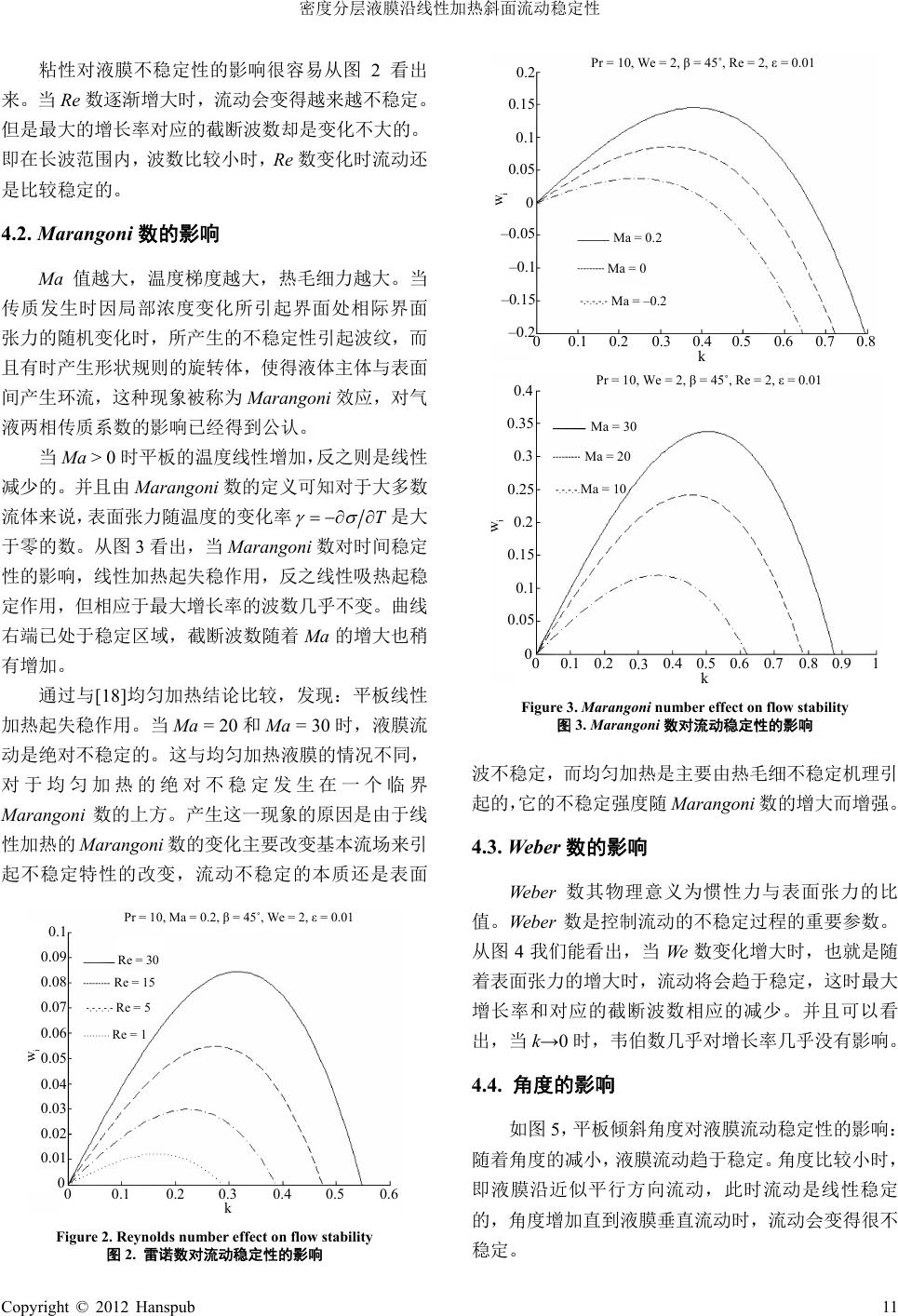 密度分层液膜沿线性加热斜面流动稳定性 粘性对液膜不稳定性的影响很容易从图 2看出 来。当 Re 数逐渐增大时,流动会变得越来越不稳定。 但是最大的增长率对应的截断波数却是变化不大的。 即在长波范围内,波数比较小时,Re数变化时流动还 是比较稳定的。 4.2. Marangoni 数的影响 Ma 值越大,温度梯度越大,热毛 细力 越大 。 当 传质发生时因局部浓度变化所引起界面处相际界面 张力的随机变化时,所产生的不稳定性引起波纹,而 且有时产生形状规则的旋转体,使得液体主体与表面 间产生环流,这种现象被称为Marangoni 效应,对气 液两相传质系数的影响已经得到公认。 当Ma > 0 时平板的温度线性增加,反之则是线性 减少的。并且由Marangoni 数的定义可知对于大多数 流体来说,表面张力随温度的变化率 T 是大 于零的数。从图 3看出,当Marangoni 数对时间稳定 性的影响,线性加热起失稳作用,反之线性吸热起稳 定作用,但相应于最大增长率的波数几乎不变。曲线 右端已处于稳定区域,截断波数随着 Ma的增大也稍 有增加。 通过与[18]均匀加热结论比较,发现:平板线性 加热起失稳作用。当 Ma = 20和Ma = 30时,液膜流 动是绝对不稳定的。这与均匀加热液膜的情况不同, 对于均匀加热的绝对不稳定发生在一个临界 Marangoni数的上方。产生这一现象的原因是由于线 性加热的 Marangoni 数的变化主要改变基本流场来引 起不稳定特性的改变,流动不稳定的本质还是表面 0.1 0.09 0.08 0.07 0.06 0.05 0.04 0.03 0.02 0.01 000.1 0.20.3 0.40.50.6 k w i Re = 30 Pr = 10, Ma = 0.2, β = 45˚, We = 2, ε = 0.01 Re = 15 Re = 5 Re = 1 Figure 2. Reynolds number effect on flow stability 图2. 雷诺数对流动稳定性的影响 0.2 0.15 0.1 0.05 0 –0.05 –0.1 –0.15 –0.2 00.1 0.20.3 0.40.50.6 0.7 0.8 k w i Pr = 10, We = 2, β = 45˚, Re = 2, ε = 0.01 Ma = –0.2 Ma = 0.2 Ma = 0 Pr = 10, We = 2, β= 45˚, Re = 2, ε= 0.01 0.4 0.3 0.2 0.1 0.4 0.50.60.70.8 0.9 0.3 0.2 0.1 00 k w i 1 0.35 0.25 0.15 0.05 Ma = 30 Ma = 20 Ma = 10 Figure 3. Marangoni number effect on flow stability 图3. Marangoni数对流动稳定性的影响 波不稳定,而均匀加热是主要由热毛细不稳定机理引 起的,它的不稳定强度随 Marangoni 数的增大而增强。 4.3. Weber 数的影响 Weber 数其物理意义为惯性力与表面张力的比 值。Weber 数是控制流动的不稳定过程的重要参数。 从图 4我们能看出,当 We 数变化增大时,也就是随 着表面张力的增大时,流动将会趋于稳定,这时最大 增长率和对应的截断波数相应的减少。并且可以看 出,当k→0时,韦伯数几乎对增长率几乎没有影响。 4.4. 角度的影响 如图 5,平板倾斜角度对液膜流动稳定性的影响: 随着角度的减小,液膜流动趋于稳定。角度比较小时, 即液膜沿近似平行方向流动,此时流动是线性稳定 的,角度增加直到液膜垂直流动时,流动会变得很不 稳定。 Copyright © 2012 Hanspub 11  密度分层液膜沿线性加热斜面流动稳定性 0.1 0.09 0.08 0.07 0.06 0.05 0.04 0.03 0.02 0.01 000.10.2 0.3 0.40.5 k w i We = 5 Pr = 10, Ma = 0.2, β = 45˚, Re = 2, ε = 0.01 We = 10 We = 20 We = 30 Figure 4. Weber number effect on flow stability 图4. 韦伯数对流动稳定性的影响 Pr = 10, Ma = 0.2, We = 2, Re = 2 0.4 0.3 0.2 0.1 0.40.5 0.60.70.8 0.9 0.3 0.2 0.1 –0.1 0 0 0.35 0.25 0.15 0.05 –0.05 β= 30˚ β= 45˚ β= 60˚ β= 90˚ k w i Figure 5. Angle number effect on f low stability 图5. 倾斜角度对流动稳定性的影响 4.5. Pr 的影响 Pr 表示热对流和热传导的影响,从图 6可以看出, 当Pr 数逐渐增大时,流动会变得越来越不稳定。 4.6. 分层效应的影响 分层效应对时间增长率的影响从图7可以看出: 在 小于 0.01 的范围内时,此时液膜的密度比较大, 其流动是稳定的,并且在这个范围内参数变化基本不 会引起流动不稳定,而随着 增大,则流动的不稳定 性越来越强,这说明随着 的增大,即随着密度的增 大,由分层效应引起的不稳定性越强。 5. 结论 本文用 N-S 方程和合理的边界条件建立密度变化 时沿倾斜线性加热平板流动液膜的控制方程及边界 条件,通过边界层理论一系列的无量纲、小扰动展开 以及正则模推导出 O-S方程及其边界条件。 在假设液膜密度为指数函数 y e 时,用摄动 法求得了密度在小参数 展开为 1 y 的假设条 件下的色散关系(波速c)的表达式。通过表达式可以看 出波速中的虚部是影响液膜流动稳定性的重要条件, 而它又是和参数Re、We、Ma、Pr 以及角度β和反映 分层效应的 等参数的变化是有关的。关于它们对流 动稳定性的影响,利用 MATLAB 进行了数值模拟分 析,最后得到结论: 1) 当波数、Pr 数、Re 数以及 Ma 数逐渐增大时 流动变得不稳定。 2) 当We数增大以及斜 面倾角越 小时流动 越 稳 定。 0.1 0.09 0.08 0.07 0.06 0.05 0.04 0.03 0.02 0.01 000.10.2 0.3 0.40.50.6 k w i Pr = 20 Re = 2, Ma = 0.2, β = 45˚, We = 2, ε = 0.01 Pr = 10 Pr = 1 Pr = 5 Figure 6. Pr number effect on flow stability 图6. Pr数对流动稳定性的影响 Pr = 10, Ma = 0.2,β= 45˚, Re = 2 0.2 0.1 0.4 0.5 0.3 0.2 0.1 00 k w i 0.25 0.15 0.05 ε= 0.2 ε= 0.1 ε= 0.05 Figure 7. Stratification effect on flow stability 图7. 分层效应对流动稳定性的影响 12 Copyright © 2012 Hanspub  密度分层液膜沿线性加热斜面流动稳定性 Copyright © 2012 Hanspub 13 3) 分层效应在 从0到0.01时,液膜流动是稳 定的,在这个范围内参数变化基本不会引起流动不稳 定;随着 增大,则流动的不稳定性越来越强,这说 明随着 的增大,即随着密度的增大,由分层效应引 起的不稳定性越强;此结论与田英[15]的研究是一致 的。 4) 平板线性加热对流动起失稳作用。与田英硕士 论文[15]均匀加热结论比较,线性加热产生Marangoni 效应,改变基本流场来引起不稳定特性的改变,流动 不稳定的本质还是表面波不稳定;而均匀加热主要由 热毛细不稳定机理引起的,它的不稳定强度随 Marangoni数的增大而增强。与胡军在力学季刊上发 表的文章[19]及其博士论文[20]中的研究是一致的。 5) 随着波数的增大,流动的不稳定性越强。 6. 致谢 感谢国家自然科学基金项目(51106132)的资助支 持! 参考文献 (References) [1] 程友良, 叶学民, 阎维平. 非线性表面张力对饱和液膜传热 稳定性的影响[J]. 华北电力大学学报, 2002, 29(2): 50-53. [2] 叶学民, 闫俊刚, 李春曦, 阎维平. 界面切应力和重力驱动下 受热过冷薄膜的破断模型研究[J]. 华北电力大学学报, 2010, 37(2): 63-68, 73. [3] 叶学民, 阎维平. 蒸发、等温或冷凝薄液膜二维表面波的通用 时空稳定性方程[J]. 中国电机工程学报, 2004, 24(3): 200- 205. [4] 阎维平, 叶学民, 李洪涛. 液体薄膜流的流动和传热特性[J]. 华北电力大学学报, 2005, 32(1): 59-65. [5] 王松岭, 张营, 李春曦, 叶学民. 切应力作用下的液膜稳定性 分析[J]. 中国电机工程学报, 2007, 27(8): 104-108. [6] 师晋生, 施明恒. 饱和下降液膜的稳定性研究[J]. 应用力学 学报, 1999, 16(4): 27-34. [7] 易家训. 分层流[M]. 北京: 高等教育出版社, 1983: 1. [8] 易家训. 流体力学[M]. 北京: 高等教育出版社, 1982: 169-173. [9] T. W. Kao. Stability of two-layer viscous stratified flow down an inclined plane. Physics Fluids, 1965, 8(5): 812-820. [10] T. W. Kao. Role of the interface in the stability of stratified flow down an inclined plane. Physics Fluids, 1965, 8(5): 2190-2194. [11] S. J. Weinstein, M. R. Kurz. Long-wavelength instabilities in three-layer flow down an incline. Physics Fluids A, 1991, 3(11): 2680-2687. [12] D. S. Loewenherz, C. J. Lawrence. The effect of viscosity stra- tification on the stability of a free surface flow at low Reynolds number. Physics Fluids A, 1989, 1(10): 1686-1693. [13] K. P. Chen. Wave formation in the gravity-driven low-Reynolds number flow of two liquid films down an inclined plane. Physics Fluids A, 1993, 5: 3038-3048. [14] 李欣. 波动液膜流动传热特性及稳定性研究[D]. 华北电力大 学, 2006. [15] 田英. 液膜流动传热特性及影响因素分析[D]. 华北电力大学, 2007. [16] A. Samanta. Stability of inertialess liquid film flowing down a heated inclined plane. Physicsand Applied Mathematics Unit, Indian Statistical Institute, 2008: 235-246. [17] A. Samanta. Stability of liquid film falling down a vertical non- uniformly heated wall. Physicsand Applied Mathematics Unit, Indian Statistical Institute, 2008: 15-23. [18] Y. L. Cheng, X. C. Fan and Y. Tian. Effect of stratification on stability of flow and heat transfer in the liquid film flowing down an inclined heated plate. Modern Physics Letters B, 2010, 24(13): 1461-1465. [19] 胡军, 胡国辉, 孙德军等. 薄膜沿加热平板下落的稳定性分 布[J]. 力学季刊, 2003, 24(1): 23-29. [20] 胡军. 薄膜沿加热平板下落的稳定性及其时空演化[D]. 中国 科学技术大学, 2004. |