Advances in Psychology
Vol.05 No.06(2015), Article ID:15520,10
pages
10.12677/AP.2015.56048
Multidimensional Item Response Theory: Psychometric Models, Parameter Estimation and Application
Peng Wang*, Xinli Zhu, Fang Wang
School of Psychology, Shandong Normal University, Jinan Shandong
Email: *pengsdnu@163.com
Received: Jun. 3rd, 2015; accepted: Jun. 23rd, 2015; published: Jun. 26th, 2015
Copyright © 2015 by authors and Hans Publishers Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/



ABSTRACT
Multidimensional Item Response Theory (MIRT) is the new development of modern psychometric theories. The psychometric models, parameter estimation and application of MIRT are overviewed in this paper. It is concluded that the development of MIRT models should be combined with cognitive construct, the method of MCMC should be used to enhance the parameter estimation of MIRT, the research of the mixed MIRT should be strengthened, and the method of maximum information should be used to get the total score of a test.
Keywords:Multidimensional Item Response Theory, Psychometric Model, Parameter Estimation
多维项目反应理论的计量模型、参数估计及应用
王鹏*,朱新立,王芳
山东师范大学心理学院,山东 济南
Email: *pengsdnu@163.com
收稿日期:2015年6月3日;录用日期:2015年6月23日;发布日期:2015年6月26日

摘 要
多维项目反应理论是现代心理测量理论的新发展,文章对多维项目反应理论的计量模型、参数估计及应用进行了综述,认为多维项目反应理论模型开发应与认知结构相结合,马尔科夫链蒙特卡洛方法能较好地实现多维项目反应理论的参数估计,应加强多种题型、多种多维项目反应模型结合的参数估计研究,建议使用基于最大信息量法的多维项目反应理论模型计算测验的总分。
关键词 :多维项目反应理论,计量模型,参数估计

1. 引言
相对经典测验理论(Classic Test Theory, CTT)而言,项目反应理论(Item Response Theory, IRT)在项目和测验质量分析、题库建设、计算机自适应测验编制等方面的作用,越来越受到研究者的青睐 (戴海琦,2010) 。近年来,随着认知科学、数学和计算机科学的发展,IRT模型的假设、理论和实际应用也出现一些新的进展,其中之一就是由以往注重单维模型(Unidimensional IRT, UIRT)向单维和多维模型(Multidimensional IRT, MIRT)并重转变。MIRT的提出是为了更好地对被试在完成一项测验任务时需要的多种能力、项目特征与答对概率之间的关系进行模型化。MIRT被认为是近20年来测验理论发展的主要新进展之一 (康春花,辛涛,2010) 。被试在对某一特定测验题目作答时,可能使用了不只一种能力;同样地,考试中的问题很可能需要许多技能和能力才能答对。特别是测量复杂的知识领域如自然科学时更是如此。尽管UIRT在一定条件下是有用的,但还是需要更复杂的IRT模型以准确反映被试和题目之间相互作用的复杂性。MIRT模型的发展正符合这一需要 (康春花,辛涛,2010) 。
2. 多维项目反应理论的计量模型
Bock,Horst,McDonald,Samejima等学者的研究工作,推动了MIRT的发展。MIRT的数学表达式包括多个描述测验中体现的被试知识和能力特征的参数,以及项目难度和区分度等题目特性的参数
(Reckase, 2009)
。MIRT建立的是被试在多维空间中的位置与其项目作答概率之间的关系。根据能力各维度 之间的关系,目前有两种主要的MIRT模型。
之间的关系,目前有两种主要的MIRT模型。
如果模型基于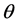 各维度的线性组合,这种线性组合可用在正态肩形函数或逻辑斯蒂克函数中,并通过这些函数来表示对某反应的概率。这意味着同样的总和可由很多种
各维度的线性组合,这种线性组合可用在正态肩形函数或逻辑斯蒂克函数中,并通过这些函数来表示对某反应的概率。这意味着同样的总和可由很多种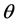 维度的组合得到。如果某一个
维度的组合得到。如果某一个 维度值较低,其它值相当高的维度
维度值较低,其它值相当高的维度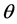 仍然可以使总和维持不变。具有这种性质的模型一般被称为“补偿模型”(compensatory models)。
仍然可以使总和维持不变。具有这种性质的模型一般被称为“补偿模型”(compensatory models)。
另一种模型的特点是,每一个题目涉及的认知任务可以分割成几个部分构成,每一个部分的作答概率可以使用单维IRT模型表示。而正确回答题目的概率则是每一部分概率的乘积。事实上,正确作答项目的概率肯定不会高于作答每一部分的最大概率,这降低了高维度值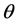 对低维度值
对低维度值 的补偿。这类模型被称为“非补偿模型”(noncompensatory models)。但一个高维度值的
的补偿。这类模型被称为“非补偿模型”(noncompensatory models)。但一个高维度值的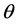 确实能产生相对较高的作答概率,有一定程度的补偿作用,所以
Reckase (2009)
也把这种模型称为“部分补偿模型”(partially compensatory models)。
确实能产生相对较高的作答概率,有一定程度的补偿作用,所以
Reckase (2009)
也把这种模型称为“部分补偿模型”(partially compensatory models)。
除了补偿和非补偿这种分类,MIRT也可以根据题目记分的形式分为二分模型和多级模型。下面结合这两种分类方法,对MIRT模型进行介绍。
2.1. 二分法记分的MIRT模型
由于探讨二分数据因素结构的需要,二分数据的MIRT模型通过扩展二分UIRT的形式开始出现 (Yao, Schwarz, 2006) 。
2.1.1. 补偿模型
2参数逻辑斯蒂克模型(M-2PL)的多维扩展形式可表示为:

其中,e的指数部分向量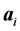 和
和 的运算方式是:
的运算方式是:
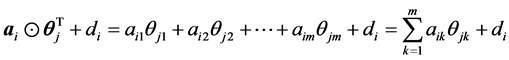
其中m为维度个数。该指数部分是向量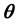 元素的线性组合,参数d是截距项,向量
元素的线性组合,参数d是截距项,向量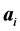 的元素作为斜率参数。
的元素作为斜率参数。
显然,MIRT的被试参数和项目参数要比同样形式的UIRT多很多,但由于补偿模型的各 元素之间有互补关系,所以可将各
元素之间有互补关系,所以可将各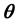 元素视为一个整体,与其对应的项目参数可以多维项目参数的形式表示。
Reckase (1985)
提出多维项目区分度(Multidimensional Item Discrimination, MDISC)和多维项目难度(Multidimensional Item Difficulty, MID)的表达式:
元素视为一个整体,与其对应的项目参数可以多维项目参数的形式表示。
Reckase (1985)
提出多维项目区分度(Multidimensional Item Discrimination, MDISC)和多维项目难度(Multidimensional Item Difficulty, MID)的表达式:
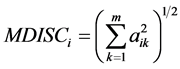
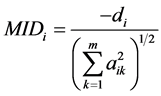
 和
和 的值和UIRT模型中的a参数和b参数有相同的解释。在M-2PL中,
的值和UIRT模型中的a参数和b参数有相同的解释。在M-2PL中,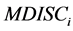 是
是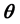 空间中,从原点出发到项目反应概率曲面上最大斜率点的方向斜率,是各维度综合区分能力的体现。
空间中,从原点出发到项目反应概率曲面上最大斜率点的方向斜率,是各维度综合区分能力的体现。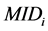 是
是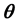 空间从原点沿最大斜率点的方向到作答概率0.5的等高线的距离。
空间从原点沿最大斜率点的方向到作答概率0.5的等高线的距离。
在多维3参数逻辑斯蒂克模型(M-3PL)中,伪猜测参数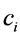 的意义变为
的意义变为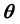 向量各维度值都极低时的答对概率
(Reckase, McKinley, 1991)
。M-3PL 的形式为:
向量各维度值都极低时的答对概率
(Reckase, McKinley, 1991)
。M-3PL 的形式为:
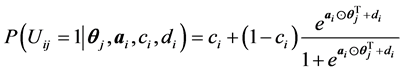
此外,在二分法记分的多维扩展模型中,还有多维Rasch模型 (Adams, Wilson, Wang, 1997) 、多维正态肩形模型 (Bock, Schilling, 2003) 。这些多维模型都是补偿模型,也可用于探索性或验证性非线性因素分析。
2.1.2. 非补偿模型
补偿模型的特点是,即使另外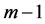 个维度值都很低,被试如果在m维度上值很高,那么仍然可以在项目上有很高的正确作答概率。但有些题目不符合上述情况,如做一道数学题需要数学计算和阅读两种能力,数学计算能力很高的人如读不懂题目,仍然无法答对题目。根据这种情况,
Sympson (1978)
提出了下面的多维模型。
个维度值都很低,被试如果在m维度上值很高,那么仍然可以在项目上有很高的正确作答概率。但有些题目不符合上述情况,如做一道数学题需要数学计算和阅读两种能力,数学计算能力很高的人如读不懂题目,仍然无法答对题目。根据这种情况,
Sympson (1978)
提出了下面的多维模型。
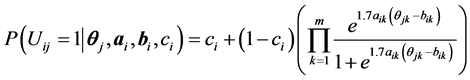
上式中,连乘部分采用的是2参数逻辑斯蒂克模型,连乘的每一部分各代表成功完成项目的一个维度任务的概率,项目的这些维度任务被认为是相互独立的,所以项目的答对概率采取了乘积的形式。但Sympson认为每个题目只有一个非零的下渐近线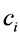 ,对每个题目不同的维度任务来说,没有相应的“伪猜测参数”。
,对每个题目不同的维度任务来说,没有相应的“伪猜测参数”。
实际上,上式是在3PL模型的基础上扩展成多维的,后来也有研究者使用了更简化的模型, Whitely (1980) 称之为多成分潜在特质模型(multicomponent latent trait model, MLTM), Maris (1995) 称之为“连接式Rasch模型”(conjunctive Rasch model),用以表示多个相互独立的认知成分对一个题目作答正确概率的影响,其表达式为:
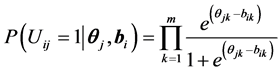
补偿模型和非补偿模型在人-题交互作用的表达方式上是不同的。非补偿模型使用的题目由不同的维度任务构成,这些不同的维度任务又对应着各自需要的技能或知识,题目的完成依赖于每个维度任务的完成。补偿模型则更侧重整体的作用,所有技能和知识一起对题目的所有方面发生影响。这方面的比较研究不多,如 Bolt和Lall (2003) 发现在英语用法测验中,补偿模型对数据的拟合比非补偿模型好。归根到底,使用哪种模型取决于人们在实际题目上的反应机制。
2.2. 多级记分的MIRT模型
二分法记分的MIRT模型已有多年的发展,但多级记分的MIRT模型的研究相对较晚。到目前为止,有关研究也仅限于补偿模型的探讨。 Muraki和Carlson (1993) 扩展得到了多维等级反应模型,近年还有研究在一套混合记分的测验中综合应用了多维3参数逻辑斯蒂克模型和多维拓广分部评分模型 (Yao, Schwarz, 2006) 。
2.2.1. 多维分部评分模型
多维分部评分模型(MPCM)是将Rasch模型扩展到多维多级的形式 (Kelderman, Rijkes, 1994) ,可表示为:
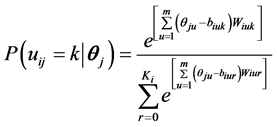
其中,
 是项目i的维度为u、类别为k的难度参数,
是项目i的维度为u、类别为k的难度参数,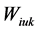 是预先确定的项目i在维度为u、类别为k的权重。
是预先确定的项目i在维度为u、类别为k的权重。
2.2.2. 多维拓广分部评分模型
分部评分项目i,能力向量为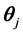 的被试,在MGPC中作答类别为k-1的概率为
(Yao, Schwarz, 2006)
:
的被试,在MGPC中作答类别为k-1的概率为
(Yao, Schwarz, 2006)
:
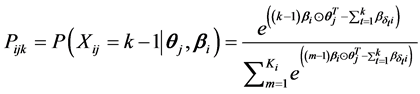
其中
 指被试j对项目i的作答类别。
指被试j对项目i的作答类别。
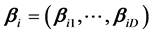 指维度数为D的项目区分度参数向量。
指维度数为D的项目区分度参数向量。
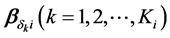 指阈限参数(或称a参数),令
指阈限参数(或称a参数),令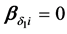 。
。
Yao和Schwarz (2006) 对此类模型考察,其参数估计方法已由体现Rasch模型特色的条件极大似然估计(CML)变成了马尔可夫链-蒙特卡洛方法(MCMC)。Yao和Schwarz分别使用了多维3参数逻辑斯蒂克模型(M-3PL)和多维拓广分部评分模型对多重选择题和论文式题目进行了参数估计。Yao和Schwarz对多维模型的项目参数、项目信息量、测验信息量、拟合评价等问题进行了较全面的计算。
2.2.3. 多维等级反应模型
Muraki和Carlson (1993) 将单维等级反应模型扩展为多维模型,项目反应函数使用的是正态肩形模型的形式。和单维模型一样,多维模型也假定题目作答由一些步骤构成,能做到第k步,必然已经成功完成前k-1步。这类模型也可用于后面类别包括前面所有类别的评定量表。比如,要评定一下在某项目上用的时间,如果某一个评定类别是“用了一个小时”,则意味着所有低于一个小时的类别均包含在内。多维等级反应模型计算被试得k分的概率与单维模型相似,其表达式为:
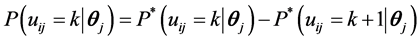
其中 ,
,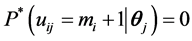
等级反应模型的正态肩形模型形式是,

将式1-4-24代入1-4-23,可得,
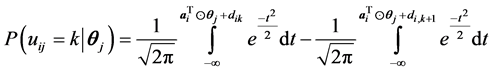
上述各种模型都只适用于某一种情况,如题目二分或题目多级,包括或不包括伪机遇参数等。但实际考试中,为提高测验的有效性,往往将不同类型的题目结合在一起使用。目前单参数逻辑斯蒂克模型和分部评分模型、2参数逻辑斯蒂克模型和等级反应模型等的结合,已用于混合项目类型(mixed item types)的测验 (Baker, Kim, 2004) 。但目前MIRT的混合项目类型的研究较为少见。
杨向东(2010) 认为,现有心理测量学模型,缺少实质理论的支持。他认为,揭示一般规律的认知研究与揭示个别差异的测量学研究相整合,构建认知测量模型(cognitive psychometric model),是将来模型发展的方向。事实上,前文提到的补偿模型和非补偿模型,在一定程度上也体现了被试问题解决过程的认知模型与心理测量学模型结合的特点。但还需要进一步结合具体领域的认知加工模型,并在测验开发之初就根据认知模型编制测验,在此基础上依据经验数据进行验证。另外,认知测量模型还需逐渐与具体情境结合,以解决复杂认知领域的建模、分析和解释等问题。这里并不是主张抛弃这些心理测量学模型,而是要加强实质性的认知加工模型与心理测量学模型之间的联结。
3. 多维项目反应理论模型的参数估计方法
3.1. 常见的参数估计方法
在项目反应理论发展过程中,出现的参数估计方法主要有 (Baker,Kim,2004;漆书青,2003) :条件极大似然估计(conditional maximum likelihood estimation, CMLE)、联合极大似然估计(joint maximum likelihood estimation, JMLE)、边际极大似然估计/EM算法(marginal maximum likelihood estimation and an EM algorithm, MMLE/EM)、边际贝叶斯估计(marginalized Bayesian estimation, MBE)等。
上述方法,基于UIRT的参数估计提出,有的后来逐渐用于MIRT的参数估计。特别是结合几个MIRT分析的统计软件,如TESTFACT
(Bock, Schilling, 2003)
、NOHARM
(Fraser, McDonald, 1988)
、ConQuest
(Wu, Adams, Wilson, 1997)
、POLYFACT
(Muraki, 1999)
等,降低了掌握统计学知识的要求,这些方法的使用者也越来越多。TESTFACT采用的估计方法是边际极大似然估计/EM算法,可用项目间四分相关(interitem tetrachoric correlations)对二分法记分项目进行因素分析。该软件使用的MIRT模型是多维2参数正态肩形模型,可得到项目和被试参数,使用者如输入下渐近线的信息,也可运行多维3参数正态肩形模型,但程序不能估计伪猜测参数,同时TESTFACT的维度数限制为15。NOHARM (Normal-Ogive Harmonic Analysis Robust Method)也是MIRT软件的代表之一。NOHARM的参数估计与TESTFACT不同,它通过被试-项目矩阵来拟合多维肩形补偿性MIRT模型,拟合时采用的是多项式近似、未加权最小二乘法,可进行探索性因素分析,其维度数可达到50。但NOHARM不提供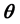 的估计值,所以,可通过NOHARM得到项目参数估计,然后输入TESTFACT得到能力参数估计。ConQuest主要用于估计Rasch模型一族的参数,这种项目和被试参数的估计有可观察的充分统计量。ConQuest能估计Rasch模型的MIRT扩展形式的参数,处理二分法记分的数据,采用的估计方法是极大似然估计。POLYFACT能处理多级数据,使用的模型是多维等级反应模型或拓广分部评分模型;它使用的是边际极大似然估计,执行的是验证性的参数结构,将题目与某一个特定维度相关联。
的估计值,所以,可通过NOHARM得到项目参数估计,然后输入TESTFACT得到能力参数估计。ConQuest主要用于估计Rasch模型一族的参数,这种项目和被试参数的估计有可观察的充分统计量。ConQuest能估计Rasch模型的MIRT扩展形式的参数,处理二分法记分的数据,采用的估计方法是极大似然估计。POLYFACT能处理多级数据,使用的模型是多维等级反应模型或拓广分部评分模型;它使用的是边际极大似然估计,执行的是验证性的参数结构,将题目与某一个特定维度相关联。
上述软件是应用较广的MIRT分析工具,可以发现,这些软件包括的MIRT模型还相对较少;有的软件不能同时输出项目参数估计和能力参数估计;还有的软件对模型的维度数量有一定的限制;主要处理二分数据的情形;还不能处理测验中包括混合记分类型题目的情况。这些软件的局限性,在一定程度上是由参数估计方法决定的,当IRT模型中的参数的个数或维度过多时,上述参数估计方法可能难于或无法实现模型的参数估计。在马尔科夫链蒙特卡洛方法(MCMC)引入IRT参数估计研究之后,许多复杂、高维模型的参数估计成为可能,MCMC方法是一种全新的参数估计方法 (Baker,Kim,2004;涂冬波,漆书青,蔡艳,戴海琦,丁树良,2008) 。下面介绍用于IRT参数估计的MCMC方法及其软件的研究情况。
3.2. 基于MCMC方法的参数估计
MCMC方法是一种动态的计算机模拟技术,它是根据任一多元理论分布,特别是以贝叶斯推断为中心的多元后验分布来模拟随机样本的一种方法。Monte Carlo方法的一个基本步骤是产生随机数,使之服从一个概率分布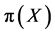 。目前常用的MCMC方法,包括Metrophs-Hasting (M-H)方法和Gibbs方法。M-H方法就是在以
。目前常用的MCMC方法,包括Metrophs-Hasting (M-H)方法和Gibbs方法。M-H方法就是在以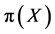 为平稳分布的马尔科夫链上产生相互依赖的样本。MCMC方法本质上是一个Monte Carlo综合程序,它的随机样本的产生与一条马尔科夫链有关。基于条件分布的迭代取样是另外一种重要的MCMC方法,其中最著名的特殊情况就是Gibbs抽样,它的特征是其潜在的马尔科夫链是通过分解一系列条件分布建立起来
(赵琪,2007)
。MCMC方法估计IRT参数的基本特点是:采用能力参数和项目参数交替迭代的方法生成马尔科夫链;然后采取截然不同于极大似然法的思路,发挥计算机模拟技术的优势,采集足够大的状态样本,用初等的方法来估计模型参数,避开了EM算法中的复杂计算,提高了估计的成功率
(王权,2006)
。
为平稳分布的马尔科夫链上产生相互依赖的样本。MCMC方法本质上是一个Monte Carlo综合程序,它的随机样本的产生与一条马尔科夫链有关。基于条件分布的迭代取样是另外一种重要的MCMC方法,其中最著名的特殊情况就是Gibbs抽样,它的特征是其潜在的马尔科夫链是通过分解一系列条件分布建立起来
(赵琪,2007)
。MCMC方法估计IRT参数的基本特点是:采用能力参数和项目参数交替迭代的方法生成马尔科夫链;然后采取截然不同于极大似然法的思路,发挥计算机模拟技术的优势,采集足够大的状态样本,用初等的方法来估计模型参数,避开了EM算法中的复杂计算,提高了估计的成功率
(王权,2006)
。
多参数、高维度IRT模型的参数估计,能较充分发挥MCMC方法的优势。国内外研究者已开始将MCMC方法用于MIRT的参数估计。 Jiang (2005) 采用MCMC方法的Gibbs抽样估计多维3参数逻辑斯蒂克模型的项目参数和被试参数。通过模拟研究考察了1个维度、2个维度和5个维度的情况。均方根误差(Root Mean Square Error, RMSE)结果显示,MCMC方法估计的精度较高。Jiang将自编MCMC程序与TESTFACT的估计结果进行了比较,发现前者的估计精度优于后者。 Zhang (2007) 也试图找到一种估计补偿性多维模型项目参数的合理方法。MCMC方法的估计结果中,项目区分度和难度的精度很高,伪猜测参数的精度相对较好。但作者对MCMC方法的计算负荷表示了担忧,如一般1条链的迭代要10,000次以上。初值的设置更接近项目参数,可能会减少计算负荷。 Bolt和Lall (2003) 使用MCMC方法比较了多维补偿模型(M-2PL)和多维非补偿模型(MLTM)的参数估计。采用模拟研究考察两种模型参数的返真性,设置样本(1000, 3000),项目数量(25, 50),能力维度之间的相关(0.0, 0.3, 0.6)。结果显示,采用MCMC的M-H算法能够保证两类模型较高的返真性,但MLTM随着能力维度相关的变高返真性变低。 付志慧(2010) 探讨了多维3参数逻辑斯蒂克模型的Gibbs抽样法,模拟实验表明,由Gibbs抽样所得的Bayes后验估计及其标准差与BILOG-MG软件所得结果是具有可比性的;还研究了多维等级反应模型下MCMC方法对含缺失数据的参数估计,发现在项目参数估计过程忽略缺失数据会带来相当大的偏差,而且待测潜在特性和缺失数据的相关性越强,偏差越大;反之,如不忽略缺失,并对缺失过程建模,偏差会减少。
目前,多数研究者用MCMC方法估计MIRT项目参数和被试参数,一般是以自编程序,或通过WinBUGS执行MCMC过程,一段程序一般考察一个多维模型,未能实现对混合记分项目类型的题目参数和被试参数联合估计,亦即不能解决两个或两个以上MIRT模型同时估计的问题。Yao等人开发的BMIRT (Bayesian Multivariate Item Response Theory)软件,为问题的解决提供了一种选择 (Reckase, 2009; Yao, Schwarz, 2006) 。BMIRT用MCMC方法中的M-H算法,估计多种MIRT模型的项目和被试参数,可处理二分和多级数据,并能实现混合记分项目类型中多个MIRT模型的同时估计,现对其进行简要介绍。
BMIRT使用的是MCMC方法中的M-H算法,其目标是通过一个稳定的分布模拟观察数据。所以,马尔科夫链的稳定分布是给定作答矩阵的模型参数的后验分布。
所有项目参数矩阵可表示为:
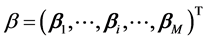
则似然方程是,

如测验中有混合记分类型题目,则1-4-27式中的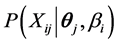 可根据不同的MIRT模型计算。
可根据不同的MIRT模型计算。
记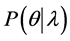 为某被试群体能力分布,分布参数为λ。譬如θ符合正态分布,则
为某被试群体能力分布,分布参数为λ。譬如θ符合正态分布,则 ,
, 为平均数,
为平均数,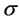 为方差和协方差矩阵。应用贝叶斯原理,其联合后验分布可写为,
为方差和协方差矩阵。应用贝叶斯原理,其联合后验分布可写为,
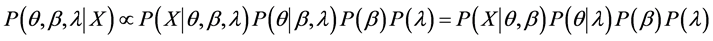
其中,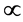 代表“正比于”。
代表“正比于”。
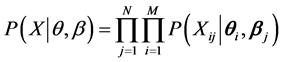

MCMC方法中的转移核t (transition kernel)是在某个给定当前参数值的状态的条件密度:
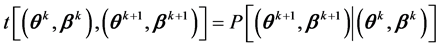
其中上标k和k + 1表示前一状态和后一状态。在BMIRT中,将转移核设置为两个条件概率的乘积:
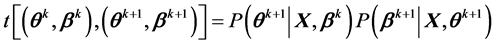
因为转移核分成了两个成分,对观察值的抽样也可以分两步。第一步从条件分布中抽取 ;然后这些抽取的值可以设定项目参数的条件分布。
;然后这些抽取的值可以设定项目参数的条件分布。
如果转移核可以用于马尔科夫链的模拟步骤,那么每一步的观察数据作为一个抽样样本保存,一般需要很长的马尔科夫链才能达到稳定分布。有时初始值的设置也会影响结果。在迭代初期的观察数据一般应予丢弃,这一阶段叫做“烧制”(burn-in)阶段。“burn-in”阶段之后的观察数据,用来估计稳定分布的项目参数和被试参数。分布的标准差即为参数估计的标准误。
基于MCMC方法进行参数估计,BMIRT还可以使用对含有缺失值的二分、多级数据,以及M-2PL、M-3PL、M-PCM、M-GRM等进行同时估计。在同样条件下与TESTFACT、NOHARM等软件进行比较,有良好的参数返真性。BMIRT在处理参数较多的多级、高维、混合模型时优势比较明显。
4. 多维项目反应理论在测验分析中的应用
随着MIRT的参数估计问题得以解决,它在测验分析中的应用价值也通过相关研究体现出来。MIRT有助于理解项目和测验究竟测什么这个问题,能够分析不同能力维度的区分能力,并可以报告被试在各个能力维度上的表现 (Zhang, 2007) 。MIRT几乎涵盖了UIRT发挥作用的所有方面,如测验结构效度证据、测验记分、测验等值 (谢晶,张厚粲,2009) 、计算机化自适应测验开发(computerized adaptive test, CAT)、项目功能差异检测(differential item functioning, DIF),等等。根据本文的目的,这里主要综述MIRT在测验结构效度证据、测验记分两方面的研究。
4.1. 多维项目反应理论的结构效度证据研究
检验测验的维度,为测验提供结构效度证据,几乎是目前文献中MIRT应用的最多的情况。
Akerman (1992) 认为根据项目参数(如区分度参数)所表示的每个项目向量的角度代表了该项目测量哪个能力维度。一个测验最有效的项目,可以从项目向量图中发现。也就是说,测量相似能力维度的有效项目应在一个范围明确的扇区中,Akerman称之为“效度扇区”。
基于IRT的项目因素分析,亦称“全息项目因素分析”(Full-information item factor analysis),能充分利用每名被试的作答向量,可深入考察潜在因素的数量 (Bock, Gibbons, Muraki, 1988) ,越来越受到研究者的重视。目前,为进一步考察特定潜在特质的多维性,研究者们借MIRT的一种简化形式——双因子模型(Bifactor Model),逐渐积累着相关的证据 (Gibbons, Bock, Hedeker, et al., 2007) 。双因子分析模型要求:每个题目在普通因素(the general factor)(下面矩阵的第一列)上都有非零负荷;但每个题目仅在一个群因素(the group factors)上有非零负荷;普通因素之间及与群因素之间正交。双因子模型的一个优势就是能够简化似然方程 (Akerman, 1992) 。

这种结构在教育、心理测量中并不少见,如阅读理解测验往往考核一个主要的目标技能和不同段落内容体现的多种知识领域技能 (Gibbons, Hedeker, 1992) 。可以说,涉及到题组或分量表的教育与心理测验,往往都可以通过MIRT的双因子模型考察其结构。如, Fukuhara (2009) 通过双因子结构的MIRT分析了带有题组的数据,模拟研究表明对题目效应以及DIF的考察可获得较高的精度。以往研究已考察了双因子模型与多维Samejima等级评分模型的结合,显然,双因子模型也可以与其他MIRT模型相结合,如前文提到的多维分部评分模型等。
在分析测验维度时,如何判断不同维度对数据的拟合情况,是很有争议的问题。
Berger和Knol (1990)
用模拟数据比较了MIRT的几种拟合指标,结果显示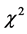 检验相对不可信,
检验相对不可信,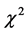 差异、AIC (Akaike’s information criterion)指标表现较好,但仍需更多的研究确认。另外,区分度参数矩阵的结构也是非常重要的参考信息。
差异、AIC (Akaike’s information criterion)指标表现较好,但仍需更多的研究确认。另外,区分度参数矩阵的结构也是非常重要的参考信息。
4.2. CTT、UIRT、MIRT在测验记分中的应用的比较
由于测验理论的发展,有的测验使用者主要基于CTT的方法记分,有的则开始使用IRT方法指导测验记分。下面结合CTT、UIRT、MIRT框架,介绍不同记分方法的比较研究。
在CTT框架中,将被试在每个题目上的得分累加得到总分是一种常见的方式,这种分数实际上将每一个题目的得分视为同等精度、同等重要的分数,显然与客观情况不符。 Rotou等人(2001) 假定真分数已知,通过模拟标准化测验的二分数据,比较CTT方法未加权得分、CTT方法加权得分与MIRT方法得分对真分数的“返真性”。其中CTT的加权是被试项目得分乘以项目与总分的点二列(point biserial)相关累加起来,MIRT的得分是根据项目反应函数计算的正确作答概率累加之和。结果显示,基于MIRT方法的加权分的返真性优于CTT未加权方法和加权方法。
DeMars (2005) 用Bifactor方法、MIRT、UIRT对包括两个分测验(subscale)的考试进行了分析,发现所有方法计算出的得分相关几乎都很高,但UIRT计算出的得分与其他结果的相关较低。由于实测数据无法比较三种方法的优劣,Demars又使用模拟数据评价三种估计方法的项目偏差(Bias)和均方根误差(RMSE),发现UIRT的Bias和RMSE最大,而Bifactor和MIRT估计的精度较高、比较接近。
一般考试都由几个部分或分测验(subscale)构成,学科专家编制的考试结构与因素分析的结构往往不一致
(Reckase, 2009)
,但人们记分的时候还是习惯用考试的各部分或分测验报告分数,并在分测验得分的基础上得到总分。上述研究证明,直接用原始分累加的方法可能误差较大。
Yao (2010)
通过对几种IRT模型的比较,建议使用MIRT模型报告分测验的分数和并用基于MIRT的最大信息量法报告测验总分。Yao使用模拟和真实数据对四种方法进行比较:a) UIRT模型;b) 高阶IRT模型(HO-IRT),即维度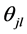 值是表示被试总能力的
值是表示被试总能力的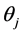 值的线性函数,
值的线性函数,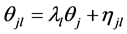 ,同时在每个分测验内部使用UIRT模型;c) MIRT模型;d) Bifactor模型。其中MIRT模型与Bifactor模型的区别是,MIRT模型不设置一个普通因素,而只是将各个分测验作为相应的维度,如Yao使用的测试包括5个分测验,则MIRT的维度为5,每个维度对应一个分测验包括的项目;Bifactor则包括6个维度,其中一个是普通因素。模拟研究显示,所有条件下参数估计、分测验得分的返真性MIRT比HO-IRT略好,但差异不大,二者比UIRT、Bifactor精度高;总分的返真性比较发现,Bifactor和UIRT的精度接近,基于最大信息量法的MIRT要显著优于Bifactor、UIRT、HO-IRT。
,同时在每个分测验内部使用UIRT模型;c) MIRT模型;d) Bifactor模型。其中MIRT模型与Bifactor模型的区别是,MIRT模型不设置一个普通因素,而只是将各个分测验作为相应的维度,如Yao使用的测试包括5个分测验,则MIRT的维度为5,每个维度对应一个分测验包括的项目;Bifactor则包括6个维度,其中一个是普通因素。模拟研究显示,所有条件下参数估计、分测验得分的返真性MIRT比HO-IRT略好,但差异不大,二者比UIRT、Bifactor精度高;总分的返真性比较发现,Bifactor和UIRT的精度接近,基于最大信息量法的MIRT要显著优于Bifactor、UIRT、HO-IRT。
5. 未来研究展望
项目反应理论考察被试特质与项目特征之间交互作用的方式,描述二者影响项目作答概率的数学模型。根据项目记分的类别,项目反应理论可分为二分法记分和多级记分两种模型;根据被试特质的维度数量,可分为单维项目反应理论和多维项目反应理论。随着模型的复杂化,模型参数的估计方法也经历了由条件极大似然估计、联合极大似然估计、边际似然估计、贝叶斯估计等的变化,近年来MCMC方法在高维、多级的多参数IRT模型中的作用,越来越受到研究者的重视 (涂冬波,蔡艳,戴海琦,丁树良,2011) 。
多维项目反应理论模型的发展需与心理学实质理论特别是认知加工理论相结合,这样不仅能发挥MIRT模型在选拨性考试、题库建设等方面的作用,而且能具体分析MIRT模型所考察的能力结构及其内部加工过程,从而为测验编制、认知诊断、补救教学等方面提供更明确的参考信息。这种途径开发的认知测量模型,将逐渐摆脱以往测验开发中“数据驱动”模型的影响。
现实测验的形式不断演变,有些复杂题目的记分类型往往不是单一的,被试体现出的实践技能一般也是多维的,需要加强多种题型、多种MIRT模型结合的参数估计研究及其他心理测量学分析。
项目反应理论在测验的误差分析方面,通过项目信息函数选取合适的项目,通过测验信息函数对特定能力点被试的估计误差进行分析,对整个测验的估计准确性进行考察,这是经典测量理论无法实现的方面;项目反应理论还可以通过MIRT对测验的维度进行分析,以提供测验结构效度证据;使用MIRT计算分测验的得分,在此基础上使用基于最大信息量法的MIRT计算测验的总分,相比其它模型的计算方法能提供较高的估计精度。
基金项目
全国教育科学“十二五”规划教育部重点2012年度课题(DIA120273)。
文章引用
王 鹏,朱新立,王 芳, (2015) 多维项目反应理论的计量模型、参数估计及应用
Multidimensional Item Response Theory: Psychometric Models, Parameter Estimation and Application. 心理学进展,06,365-375. doi: 10.12677/AP.2015.56048
参考文献 (References)
- 1. 戴海琦(2010). 心理测量学. 北京: 高等教育出版社.
- 2. 付志慧(2010). 多维项目反应模型的参数估计. 硕士论文, 吉林大学, 吉林.
- 3. 康春花, 辛涛(2010). 测验理论的新发展: 多维项目反应理论. 心理科学进展, 3期, 530-536.
- 4. 漆书青(2003). 现代测量理论在考试中的应用. 武汉: 华中师范大学出版社.
- 5. 涂冬波, 蔡艳, 戴海琦, 丁树良(2011). 多维项目反应理论: 参数估计及其在心理测验中的应用. 心理学报, 11期, 1329-1340.
- 6. 涂冬波, 漆书青, 蔡艳, 戴海琦, 丁树良(2008). IRT模型参数估计的新方法——MCMC算法. 心理科学, 1期, 177-180.
- 7. 王权(2006). “马尔科夫链蒙特卡洛”(MCMC)方法在估计IRT模型参数中的应用. 考试研究, 4期, 45-63.
- 8. 谢晶, 张厚粲(2009). 测验等值: 从IRT到MIRT. 心理学探新, 5期, 67-71.
- 9. 杨向东(2010). 测验项目反应机制与心理测量模型假设的对应性分析. 心理科学进展, 8期, 1349-1358.
- 10. 赵琪(2007). MCMC方法研究. 硕士论文, 山东大学, 济南.
- 11. Ackerman, T. A. (1994). Using multidimensional item response theory to understand what items and tests are measuring. Applied Measurement in Education, 4, 255-278.
- 12. Adams, R. J., Wilson, M., & Wang, W. (1997). The multidimensional random coefficients multinomial logit model. Applied Psychological Measurement, 21, 1-24.
- 13. Akerman, T. A. (1992). Assessing construct validity using multidimensional item response theory. Proceedings of the Annual Meeting of the American Educational Research Association, San Francisco, 20-24 April 1992.
- 14. Baker, F. B., & Kim, S. (2004). Item response theory parameter estimation techniques (2nd ed.). New York: Marcel Dekker, Inc.
- 15. Berger, M. P. F., & Knol, D. L. (1990). On the assessment of dimensionality in multidimensional item response theory models. Research Report from the Division of Educational Measure and Data Analysis, Enschede: University of Twente.
- 16. Bock, R. D., & Schilling, S. G. (2003). IRT based item factor analysis. In M. du Toit (Ed.), IRT from SSI: BILOG-MG, MULTILOG, PARSCALE, TESTFACT. Lincolnwood, IL: Scientific Software Internation-al.
- 17. Bock, R. D., Gibbons, R. D., & Muraki, E. (1988). Full-information item factor analysis. Applied Psychological Measurement, 12, 261-280.
- 18. Bolt, D. M., & Lall, V. F. (2003). Estimation of compensatory and noncompensatory multidimensional item response models using Markov Chain Monte Carlo. Applied Psychological Measurement, 27, 395-414.
- 19. DeMars, C. E. (2005). Scoring subscales using multidimensional item response theory models. Proceedings of the Annual Meeting of the American Psychological Association (ED496242), Washington DC, 18-21 August 2005.
- 20. Fraser, C., & McDonald, R. P. (1988). NOHARM: Least squares item factor analysis. Multivariate Behavioral Research, 23, 267-269.
- 21. Fukuhara, H. (2009). A differential item functioning model for testlet-based items using a bi-factor multidimensional item response theory model: A Bayesian approach. Ph.D. Thesis, Tallahassee, FL: Department of Educational Psychology and Learning Systems, Florida State University.
- 22. Gibbons, R. D., & Hedeker, D. (1992). Full information item bi-factor analysis. Psychometrika, 57, 423-436.
- 23. Gibbons, R. D., Bock, R. D., Hedeker, D., Weiss, D. J., Segawa, E., Bhaumik, D. K. et al. (2007). Full-information item bifactor analysis of graded response data. Applied Psychological Measurement, 31, 4-19.
- 24. Jiang, Y. L. (2005). Estimating parameters for multidimensional item response theory models by MCMC methods. Ph.D. Thesis, East Lansing, MI: Michigan State University.
- 25. Kelderman, H., & Rijkes, C. P. M. (1994). Loglinear multidimensional IRT models for polytomously scored items. Psychometrika, 59, 149-176.
- 26. Maris, E. (1995). Psychometric latent response models. Psychometrika, 45, 479-494.
- 27. Muraki, E. (1999). POLYFACT version 2 (Computer program). Princeton, NJ: Educational Testing Service.
- 28. Muraki, E., & Carlson, J. E. (1993). Full-information factor analysis for polytomous item responses. Proceedings of the Annual Meeting of the American Educational Research Association, Atlanta, 12-16 April 1993.
- 29. Reckase, M. D. (1985). The difficulty of test items that measure more than one ability. Applied Psychological Measurement, 30, 469-492.
- 30. Reckase, M. D. (2009). Multidimensional item response theory. New York: Springer Science + Business Media, LLC.
- 31. Reckase, M. D., & McKinley, R. L. (1991). The discriminating power of items that measure more than one dimension. Applied Psychological Measurement, 15, 361-373.
- 32. Rotou, O., Elmore, P. B., & Headrick, T. C. (2001). Number correct scoring: Comparison between classical true score theory and multidimensional item response theory. Proceedings of the Annual Meeting of the American Education Research Association, Seattle, 10-14 April 2001.
- 33. Sympson, J. B. (1978). A model for testing with multidimensional items. In D. J. Weiss (Ed.), Proceedings of the 1977 Computerized Adaptive Testing Conference. Minneapolis, MN: University of Minnesota.
- 34. Whitely, S. E. (1980). Multicomponent latent trait models for ability tests. Psychometrika, 45, 479-494.
- 35. Wu, M. L., Adams, R. J., & Wilson, M. R. (1997). ConQuest: Generalized item response modeling software. Victoria: ACER.
- 36. Yao, L. (2010). Reporting valid and reliable overall scores and domain scores. Monterey, CA: CTB/McGraw-Hill.
- 37. Yao, L., & Schwarz, R. D. (2006). A multidimensional partial credit model with associated item and test statistics: An application to mixed-format tests. Applied Psychological Measurement, 30, 469-492.
- 38. Zhang, L. T. (2007). The estimation of multidimensional item response theory models. Ph.D. Thesis, Columbia, SC: University of South Carolina.
NOTES
*通讯作者。