Pure Mathematics
Vol.4 No.05(2014), Article
ID:14075,17
pages
DOI:10.12677/PM.2014.45027
The Theory Caused by the Conditional Solution to a Type of Symmetric Nonlinear Equations
Yangtze College, East China Institute of Technology, Fuzhou
Email: 2318284432@qq.com
Copyright © 2014 by author and Hans Publishers Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/



Received: Jul. 14th, 2014; revised: Aug. 12th, 2014; accepted: Aug. 21st, 2014
ABSTRACT
This paper mainly discusses the solution under certain conditions of a class of nonlinear algebraic equations, and the definition of such equations is given; and at the same time, according to the new definition, it puts forward some new conjecture.
Keywords:The Topological Symmetry Equations

由一类对称非线性方程组的条件解所引发的
理论
周亚南
东华理工大学长江学院,抚州
Email: 2318284432@qq.com
收稿日期:2014年7月14日;修回日期:2014年8月12日;录用日期:2014年8月21日

摘 要
本文主要讨论了一类非线性代数方程组在某些条件下的解的情况,并给出了这类方程组的定义,同时,由新的定义又提出了一些新的猜想。
关键词
拓扑对称方程组

1. 引言及特殊的方程组的定义
本文是作者在研究数学史时,所发现的一个感兴趣的问题,他起源于对三角形全等的证明,当然他的证明或否定远远超出了初等数学,有关他的文献可以参考[1] 。下面给出含有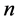 个未知量的这类方程组的定义:
个未知量的这类方程组的定义: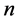 个未知量的每一个未知量定义为单元,即
个未知量的每一个未知量定义为单元,即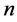 个未知量有
个未知量有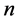 个单元。对于
个单元。对于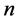 个未知量有如下的组合
个未知量有如下的组合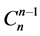 ,其中满足这种组合的未知量仅满足乘法律或者仅满足加法律,即从
,其中满足这种组合的未知量仅满足乘法律或者仅满足加法律,即从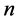 个未知量中选取
个未知量中选取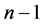 个未知量,这
个未知量,这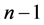 个未知量仅满足乘法律或者仅满足加法律,定义这种组合为基本组合,可知这种组合共有
个未知量仅满足乘法律或者仅满足加法律,定义这种组合为基本组合,可知这种组合共有 种,即基本组合有
种,即基本组合有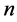 种,其中满足乘法律的基本组合定义为乘律基本组合,满足加法律的基本组合定义为加律基本组合。以集合
种,其中满足乘法律的基本组合定义为乘律基本组合,满足加法律的基本组合定义为加律基本组合。以集合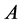 代表所有的单元,即
代表所有的单元,即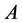 为全集,以集合
为全集,以集合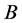 代表
代表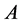 的子集,且
的子集,且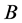 中含仅含有
中含仅含有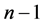 个单元,即组合
个单元,即组合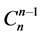 个单元,可知这
个单元,可知这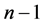 个单元仅满足乘法律或者仅满足加法律,定义
个单元仅满足乘法律或者仅满足加法律,定义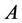 与
与 的差集为剩余集,其中剩余集所含的那个单元定义为剩余单元。定义集合
的差集为剩余集,其中剩余集所含的那个单元定义为剩余单元。定义集合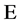 为超全集(含有
为超全集(含有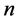 个单元),其中
个单元),其中
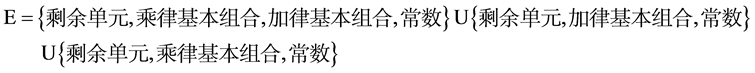
由上式知道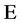 中含有四个元素或者三个元素,对超全集
中含有四个元素或者三个元素,对超全集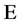 定义一种运算,对于
定义一种运算,对于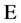 中的元素可以满足任何形式的数学运算以及混合运算,如:加法、乘法、减法、除法、对数、幂次方、根号等等,其中满足这种要求的表达式记为
中的元素可以满足任何形式的数学运算以及混合运算,如:加法、乘法、减法、除法、对数、幂次方、根号等等,其中满足这种要求的表达式记为 ,可知集合
,可知集合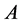 可以构造
可以构造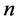 个超全集
个超全集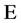 ,即
,即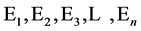 ,若
,若 个超全集
个超全集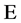 具有相同数学运算,即具有相同形式的数学表达式,我们称表达式
具有相同数学运算,即具有相同形式的数学表达式,我们称表达式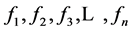 为一组拓扑对称表达式,而由
为一组拓扑对称表达式,而由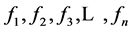 所组成的方程组称为拓扑对称方程组。若
所组成的方程组称为拓扑对称方程组。若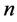 个超全集
个超全集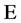 不具有相同数学运算,即不具有相同形式的数学表达式,我们称表达式
不具有相同数学运算,即不具有相同形式的数学表达式,我们称表达式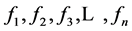 为一组拓扑非对称表达式,而由
为一组拓扑非对称表达式,而由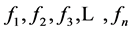 所组成的方程组称为拓扑非对称方程组。对于不满足上述任何形式的方程组,我们定义为一般拓扑方程组。
所组成的方程组称为拓扑非对称方程组。对于不满足上述任何形式的方程组,我们定义为一般拓扑方程组。
例:三个未知量 ,从中选取
,从中选取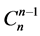 个未知量,可知共有3种,它们分别是
个未知量,可知共有3种,它们分别是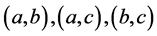 ,既有三种基本组合,又如基本组合
,既有三种基本组合,又如基本组合 满足加法律和乘法律其形式如下:
满足加法律和乘法律其形式如下: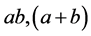 ,其中
,其中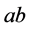 为乘律基本组合,
为乘律基本组合,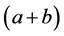 为加律基本组合。又如由单元
为加律基本组合。又如由单元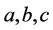 构造的下面的方程组
构造的下面的方程组
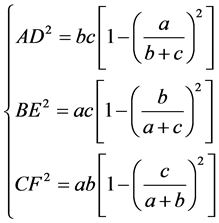 (1.1)
(1.1)
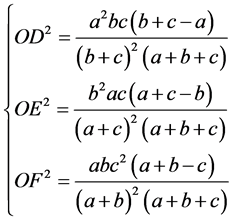 (1.2)
(1.2)
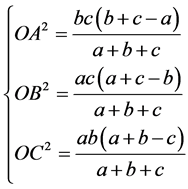 (1.3)
(1.3)
可知其为拓扑对称方程组,其中对于方程式 来说
来说 为剩余单元,其中
为剩余单元,其中

构成一个超全集。对于含有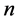 个单元的拓扑对称方程组,当这
个单元的拓扑对称方程组,当这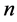 个单元同时增加相同的倍数时,这个拓扑方对称程组的每个方程式不变,即方程组不变,定义这种方程组为完全线性代数方程组,如下面含有
个单元同时增加相同的倍数时,这个拓扑方对称程组的每个方程式不变,即方程组不变,定义这种方程组为完全线性代数方程组,如下面含有 三个单元的方程组:
三个单元的方程组:
 (1.4)
(1.4)
使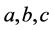 满足
满足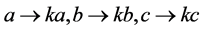 ,可知方程组(1.4)不变,即为完全线性代数方程组,这种方程组有无穷多组解,且满足
,可知方程组(1.4)不变,即为完全线性代数方程组,这种方程组有无穷多组解,且满足 ,
, 是其中一组解,
是其中一组解,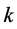 为系数,即
为系数,即 也是方程组的一组解。同样,对于含有
也是方程组的一组解。同样,对于含有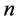 个单元的拓扑对称方程组,当这
个单元的拓扑对称方程组,当这 个单元同时增加相同的倍数时,这个拓扑方对称程组的每个方程式发生变化,方程组中的方程式
个单元同时增加相同的倍数时,这个拓扑方对称程组的每个方程式发生变化,方程组中的方程式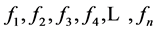 的比值:
的比值: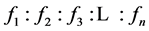 的比值不变,满足这个关系式子的方程组,定义为满足线性代数方程组。如上面的方程组(1.1)~(1.3)就是这样的方程组,即为满足线性代数方程组。本文主要讨论了方程组(1.1)(1.2)(1.3)在单元
的比值不变,满足这个关系式子的方程组,定义为满足线性代数方程组。如上面的方程组(1.1)~(1.3)就是这样的方程组,即为满足线性代数方程组。本文主要讨论了方程组(1.1)(1.2)(1.3)在单元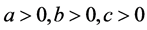 情况下的解的情况,可知方程组(1.1)(1.3)在此情况下至多有一解,方程组(1.2)在此情况下至多有两解。
情况下的解的情况,可知方程组(1.1)(1.3)在此情况下至多有一解,方程组(1.2)在此情况下至多有两解。
2. 几个引理及其证明
对于单元来说我们定义一种运算,如单元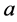 ,定义
,定义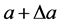 表示单元
表示单元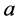 变大,即用符号
变大,即用符号 表示变大,同理可以定义
表示变大,同理可以定义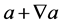 表示单元
表示单元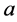 变小,即用符号
变小,即用符号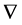 表示单元
表示单元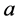 变小。下面我们再次来讨论方程组(1.2)在
变小。下面我们再次来讨论方程组(1.2)在 的情况下的解的情况。这里字母
的情况下的解的情况。这里字母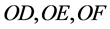 表示为不为零常数,或者赋予
表示为不为零常数,或者赋予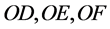 一组常数,如3,4,5。
一组常数,如3,4,5。
引理2.1:单元 满足下面三个式子
满足下面三个式子
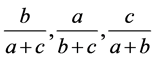 (2.1)
(2.1)
当单元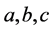 满足变化:
满足变化: 且
且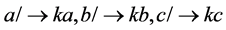 时(符号
时(符号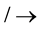 表示:不变为),式子(2.1)必有一个变大,一个变小。
表示:不变为),式子(2.1)必有一个变大,一个变小。
证明:当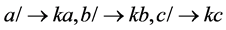 时,单元
时,单元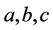 有下面几种变化组合
有下面几种变化组合
 (2.11)
(2.11)
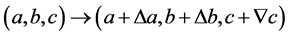 (2.12)
(2.12)
 (2.13)
(2.13)
 (2.14)
(2.14)
 (2.15)
(2.15)
 (2.16)
(2.16)
 (2.17)
(2.17)
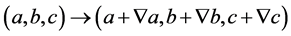 (2.18)
(2.18)
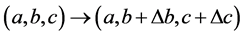 (2.19)
(2.19)
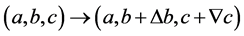 (2.20)
(2.20)
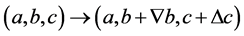 (2.21)
(2.21)
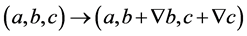 (2.22)
(2.22)
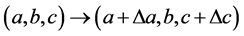 (2.23)
(2.23)
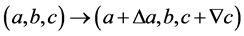 (2.24)
(2.24)
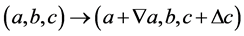 (2.25)
(2.25)
 (2.26)
(2.26)
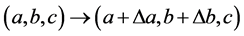 (2.27)
(2.27)
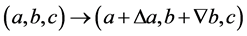 (2.28)
(2.28)
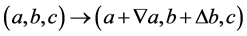 (2.29)
(2.29)
 (2.30)
(2.30)
上式(2.11)(2.18)是相似于其余各式,其证法是将满足(2.11)(2.18)的单元 同时缩小或同时增加相同的倍数,且使这种组合中的其中一个单元与上式其余组合中的一个组合满足至少有一个单元相等,则可知(2.11)(2.18)满足其余各种组合。
同时缩小或同时增加相同的倍数,且使这种组合中的其中一个单元与上式其余组合中的一个组合满足至少有一个单元相等,则可知(2.11)(2.18)满足其余各种组合。
当
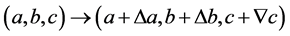 (2.12)
(2.12)
时式(2.1)满足下面的变化
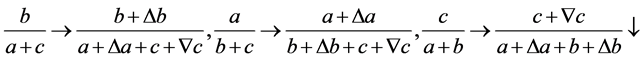
符号 表示变小,那么仅需证明
表示变小,那么仅需证明 中必有一个变大即可,将(2.12)做变化,其形式如下:
中必有一个变大即可,将(2.12)做变化,其形式如下:
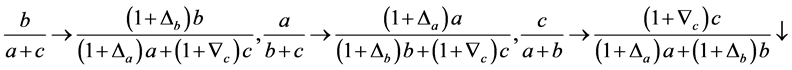
则: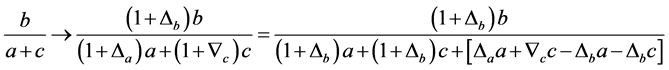
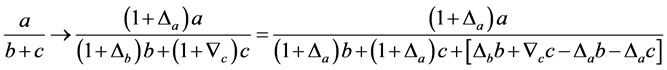
式中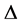 表示一个大于零的数,如
表示一个大于零的数,如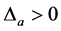 ;同样
;同样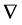 表示一个小于零的数,如
表示一个小于零的数,如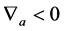 。则可知下面式子必有一个变小
。则可知下面式子必有一个变小
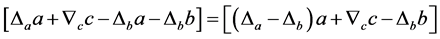

所以式子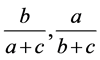 中必有一个变大,即当
中必有一个变大,即当
 (2.12)
(2.12)
式子(2.1)必有一个变大,一个变小。
当 (2.13)时,式(2.1)满足下面的变化
(2.13)时,式(2.1)满足下面的变化
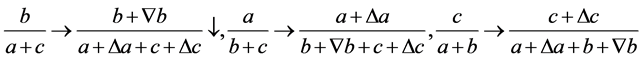
由(2.12)的证明可知当满足(2.13)时,式子(2.1)中的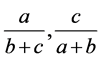 中也必有一个变大,故式子(2.1)必有一个变大,一个变小。
中也必有一个变大,故式子(2.1)必有一个变大,一个变小。
当
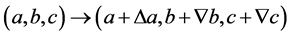 (2.14)
(2.14)
则式(2.1)满足下面的变化
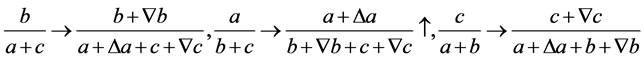
符号 表示变大,同样仅需证明
表示变大,同样仅需证明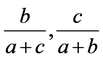 中必有一个变小即可,证明如下:
中必有一个变小即可,证明如下:

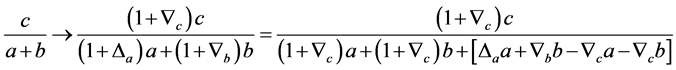
同样由上式[]可知式子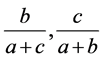 中必有一个变小。
中必有一个变小。
注释:[]代表 ,即代表中括号和其内部的算子。
,即代表中括号和其内部的算子。
当
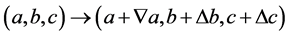 (2.15)
(2.15)
时,在形式上相似于(2.12),由于式(2.1)的对称性可知其在(2.15)的情况下必有一个变大一个变小。在下文中我们以≈代表形式上的相似,如(2.12)≈(2.15)≈(2.13),表示(2.15)(2.12)(2.13)在形式上相似,即表示单元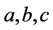 中一个变小,两个变大。若一个命题其命题和结论都相似,定义为全相似命题,可知上面的两个子命题为全相似命题。
中一个变小,两个变大。若一个命题其命题和结论都相似,定义为全相似命题,可知上面的两个子命题为全相似命题。
当
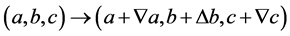 (2.16)
(2.16)
可知(2.16)≈(2.14),由于式(2.1)的对称性可知其在(2.16)的情况下必有一个变大一个变小,同样可知其二个命题为全相似命题。
当
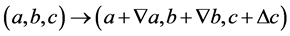 (2.17)
(2.17)
可知(2.16)≈(2.14)≈(2.17),故式(2.1)在(2.17)的情况下必有一个变大一个变小。
由上面的(2.12)(2.13)(2.14)(2.15)(2.16)(2.17)以及(2.12)≈(2.15)≈(2.13)和(5.16)≈(5.14)≈(5.17)之间的相似,以及是子命题之间的全相似命题。同样可知(2.19)(2.20)(2.21)(2.22)(2.23)(2.24)(2.25)(2.26)(2.27)(2.28) (2.29)(2.30)也存在着相似结构,可知(2.20)≈(2.21)≈(2.24)≈(2.25)≈(2.28)≈(2.29),(2.19)≈(2.23)≈(2.27),(2.22)≈(2.26)≈(2.30),可知要讨论四种情况,在这里我们讨论四种情况,由(2.20)≈(2.21)≈(2.24)≈(2.25)≈ (2.28)≈(2.29),我们讨论(2.20)和(2.21),讨论如下
当
 (2.20)
(2.20)
式子(2.1)有如下的变化
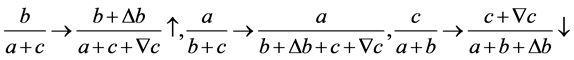
可知式(2.1)必有一个变大一个变小。
当
 (2.21)
(2.21)
式子(2.1)有如下的变化
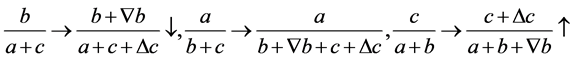
可知式(2.1)必有一个变大一个变小。
由(2.19)≈(2.23)≈(2.27),我们讨论(2.19)讨论如下:
当
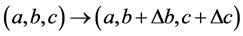 (2.19)
(2.19)
式(2.1)有下列的变化
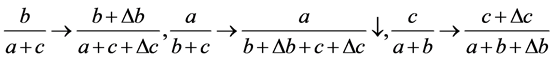
同样,我们仅需证明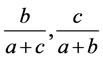 必有一个变大即可,证明如下:
必有一个变大即可,证明如下:

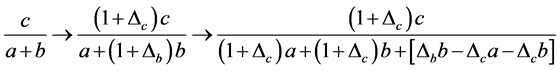
由[]可知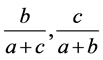 必有一个变大,故可知式(2.1)必有一个变大一个变小。
必有一个变大,故可知式(2.1)必有一个变大一个变小。
由(2.22)≈(2.26)≈(2.30),我们仅讨论(2.22),讨论如下:
当
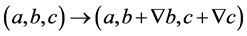 (2.22)
(2.22)
式(2.1)有如下变化
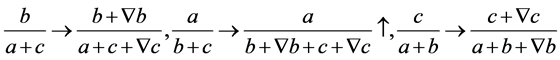
同样,我们仅需证明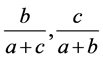 中必有一个变小即可,证明如下:
中必有一个变小即可,证明如下:

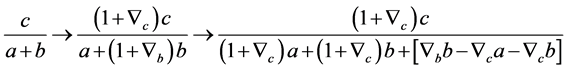
同样由[]可知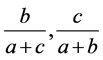 必有一个变小,故可知式(2.1)必有一个变大一个变小。故我们证明了引理1。
必有一个变小,故可知式(2.1)必有一个变大一个变小。故我们证明了引理1。
从上面的例子我们不难看出我们仅需证明(2.12)(2.14)(2.20)(2.21)(2.19)(2.22)这六种情况,满足这样一组最小的证明的子命题组数组定义为最小组,最小组的个数定义为最小基,由上面可知其中一组最小组为(2.12)(2.14)(2.20)(2.21)(2.19)(2.22),最小基为6。
对于方程组(1.2)来说,要讨论其在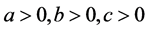 的情况下解的的情况,还必须讨论下面的引理:
的情况下解的的情况,还必须讨论下面的引理:
引理2.2:使方程组(1.2)中的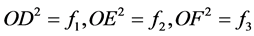 ,则下列两个命题成立
,则下列两个命题成立
(1) 若 ,那么有
,那么有 ,若还存在一个未知量
,若还存在一个未知量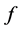 使其满足
使其满足
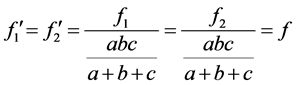 (2.2)
(2.2)
那么在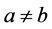 时必有
时必有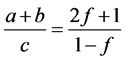 成立。
成立。
(2) 若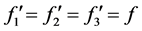 ,那么仅有
,那么仅有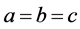 成立。
成立。
证明:(1) 当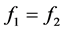 时,很明显存在
时,很明显存在 ,将上面的
,将上面的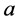 替换为
替换为 ,或者
,或者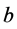 替换为
替换为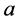 即可得证。
即可得证。
当存在一个未知量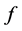 使其满足(2.2)时,则有下面的式子成立
使其满足(2.2)时,则有下面的式子成立
 (2.3)
(2.3)
由(2.3)可以得到下面的式子
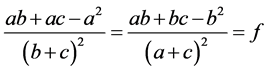 (2.4)
(2.4)
由(2.4)则可以的到下面的式子
 (2.5)
(2.5)
由(2.5)式便可得到
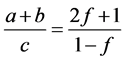 (2.6)
(2.6)
(2) 当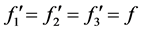 时,可知必有一解
时,可知必有一解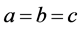 成立,下面证明其唯一性
成立,下面证明其唯一性
证明:若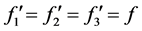 ,则可知存在下面三个关系
,则可知存在下面三个关系
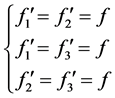 (2.7)
(2.7)
由(2.7)以及引理2.2中的(1)以及方程组的对称性可知有下列几种情况
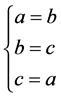 (2.71)
(2.71)
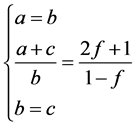 (2.72)
(2.72)
 (2.73)
(2.73)
 (2.74)
(2.74)
 (2.75)
(2.75)
 (2.76)
(2.76)
 (2.77)
(2.77)
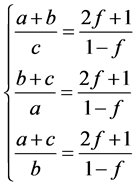 (2.78)
(2.78)
由(2.71)到(2.78),可知具有下面的相似性:
(2.72)≈(2.73)≈(2.75),(2.74)≈(2.76)≈(2.77),(2.71)≈(2.71),(2.78)≈(2.78)。
当满足(2.72)≈(2.73)≈(2.75)时,我们取(2.72),由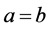 ,
,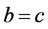 可知
可知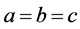 ,又因为
,又因为

现在证明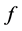 的不可能性由原方程组(1.2)可知单元
的不可能性由原方程组(1.2)可知单元 满足下面关系
满足下面关系
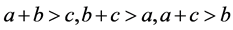
又因为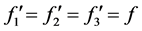 可以验证
可以验证 所以这种情况不存在。
所以这种情况不存在。
当满足(2.71)≈(2.71)时,很明显有
当满足(2.78)≈(2.78)时,有下列方程组成立

所以,当满足(2.78)≈(2.78)时,必有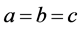 。
。
当满足(2.74)≈(2.76)≈(2.77)时,我们选取(2.74)来作为研究对象,则仅从(2.74)得到 ,又因为
,又因为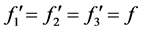 所以原方程组可以变为下列式子
所以原方程组可以变为下列式子
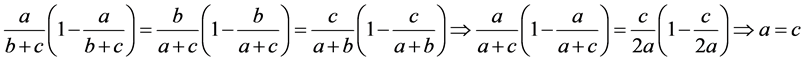
故此种情况下必有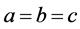 ,此时我们完全证明了引理2,证毕。
,此时我们完全证明了引理2,证毕。
3. 方程组(1.2)在 的情况下解的判定
的情况下解的判定
下面开始证明方程组(1.2)在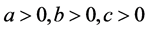 的情况下解的情况,在上面证明引理2.2时,我们引入了
的情况下解的情况,在上面证明引理2.2时,我们引入了 三个未知量去替代
三个未知量去替代 ,为了方便我们仍以
,为了方便我们仍以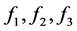 三个未知量替代
三个未知量替代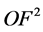
 ,因为方程组(1.2)中的方程组是满组线性代数代数方程组,若方程组在
,因为方程组(1.2)中的方程组是满组线性代数代数方程组,若方程组在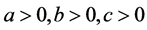 的情况下的解唯一,那么必存在其
的情况下的解唯一,那么必存在其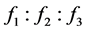 唯一,即其比值具有唯一性,于是有下列式子
唯一,即其比值具有唯一性,于是有下列式子
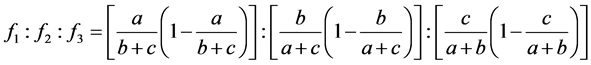 (3.1)
(3.1)
可以知道式子(3.1)满组完全线性比,由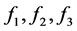 ,可知可以分为下列几种情况
,可知可以分为下列几种情况
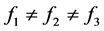 (3.11)
(3.11)
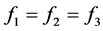 (3.12)
(3.12)
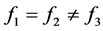 (3.13)
(3.13)
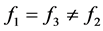 (3.14)
(3.14)
 (3.15)
(3.15)
由上面的(3.11)到(3.15)可知要讨论三种情况(3.11),(3.12),(3.13)≈(3.14)≈(3.15),于是我们讨论(3.11),(3.12),(3.13)三种情况。
Case i:当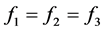 (3.12)时,由引理2.2可知必有
(3.12)时,由引理2.2可知必有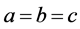 ,后代入原方程组其解具有唯一性,此时
,后代入原方程组其解具有唯一性,此时 的大小与
的大小与 的大小有关。
的大小有关。
Case ii:当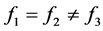 (3.13)时,由引理2.2可知要分为三种情况,如下
(3.13)时,由引理2.2可知要分为三种情况,如下
(1) 
(2) 
(3)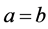 和
和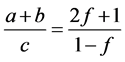 共同的情况
共同的情况
当(1)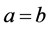 时,式子(3.1)可以变为下面的式子
时,式子(3.1)可以变为下面的式子
 (3.2)
(3.2)
当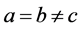 时,
时, 有下面的两种关系(1)
有下面的两种关系(1) 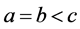 (2)
(2) 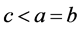
当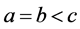 时,可知式子(2.1)满足下面的关系
时,可知式子(2.1)满足下面的关系
 (3.3)
(3.3)
下面变化 ,但必须保证
,但必须保证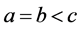 ,由(3.3)式可知当
,由(3.3)式可知当 变大时,式子(3.2)有下列变化
变大时,式子(3.2)有下列变化
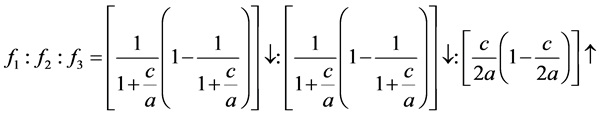
当 变小时
变小时
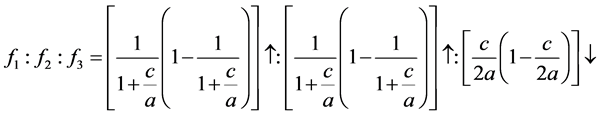
当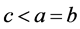 时,可知式子(2.1)满足下面的关系
时,可知式子(2.1)满足下面的关系
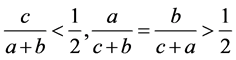 (3.4)
(3.4)
同样变化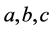 ,但必须保证
,但必须保证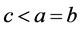 ,由(3.3)式可知当
,由(3.3)式可知当 变大时,式子(3.2)有下
变大时,式子(3.2)有下

当 变小时
变小时

当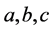 成倍增大时,
成倍增大时,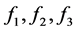 也必成倍增大,代入方程组(1.2)即可,即可知在
也必成倍增大,代入方程组(1.2)即可,即可知在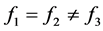 的情况下,当
的情况下,当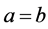 时,方程组(1.2)仅有一解在
时,方程组(1.2)仅有一解在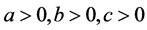 的情况下。
的情况下。
当(2) 时,将(3.1)转换为下列比例式
时,将(3.1)转换为下列比例式
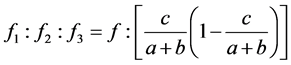 (3.5)
(3.5)
这里我们再次对(2)进行讨论,由均值不等式可知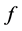 满足下列关系式
满足下列关系式
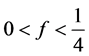 (3.6)
(3.6)
由(3.6)式可以得到下列两个式子
 (3.7)
(3.7)
由(3.7)式可以得到下列不等式

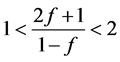
对(3.5)进行讨论,现在对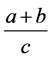 进行讨论,当
进行讨论,当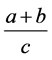 变大时,可知
变大时,可知 变小,
变小,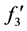 变大。当
变大。当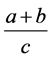 变小时,可知
变小时,可知 变大,
变大,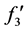 变小。可知在
变小。可知在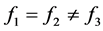 的情况下,当(2)
的情况下,当(2) 时,方程组(1.2)仅有一解在
时,方程组(1.2)仅有一解在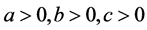 的情况下。
的情况下。
当(3)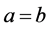 和
和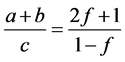 共同的情况,即当
共同的情况,即当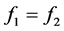 时,存在
时,存在 和
和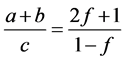 这两种情况,那么我们仅需判断,在此两种情况下的
这两种情况,那么我们仅需判断,在此两种情况下的 是否相等即可。
是否相等即可。
当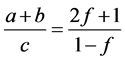 时,可知下面的式子成立
时,可知下面的式子成立
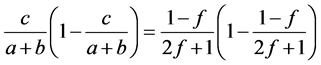 (3.8)
(3.8)
当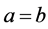 时,由式子(2.3)可以得到下面的式子
时,由式子(2.3)可以得到下面的式子
 (3.9)
(3.9)
由式子(3.9)可以得到下列两个式子
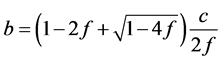 或者
或者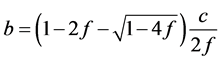 (3.10)
(3.10)
由(3.10)可以得到下面的式子
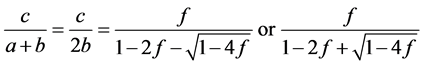 (3.12)
(3.12)
由(3.12)可以得到下面的式子
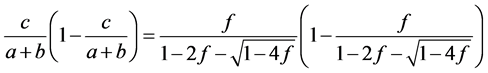 (3.13)
(3.13)
或者

由式子(3.8)和(3.12)可知此二式相等,当二式相等时,可以得到下面一个关于 的方程式
的方程式
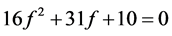 (3.14)
(3.14)
由上面式子可知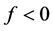 ,故不存在
,故不存在 使第三种情况成立,故当
使第三种情况成立,故当 (3.13)时,方程组(1.2)仅有一解。
(3.13)时,方程组(1.2)仅有一解。
Case iii:当(3.11)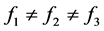 时,因为满足完全线性比,所以假定
时,因为满足完全线性比,所以假定 保持不变,讨论式子(3.1),则可知
保持不变,讨论式子(3.1),则可知 有下列几种情况
有下列几种情况
(1) 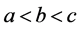 (2)
(2)  (3)
(3) 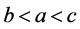 (4)
(4) 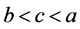 (5)
(5) 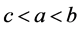 (6)
(6)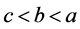
当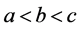 (1)时,
(1)时,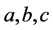 有下列的关系式子
有下列的关系式子
 或者
或者 (3.15)
(3.15)
若保持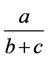 不变,则由引理1可知
不变,则由引理1可知 必发生变化,于是讨论下列三种情况
必发生变化,于是讨论下列三种情况
(1) 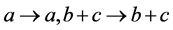
(2) 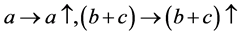
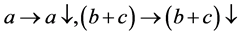
当(1)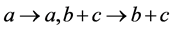 时,可知
时,可知 中必有一个变大,一个变小,于是可知式子
中必有一个变大,一个变小,于是可知式子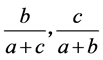 ,必有一个变大一个变小,由(3.15)可知式子(3.1)具有唯一性,又因为
,必有一个变大一个变小,由(3.15)可知式子(3.1)具有唯一性,又因为
(1)≈(2)≈(3),所以其它情况和(1)相同不做讨论。
当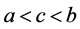 时,
时, 有下列的关系式子
有下列的关系式子
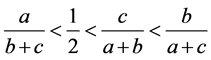 或者
或者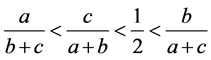 (3.16)
(3.16)
同样式子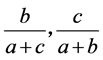 ,必有一个变大一个变小,由(3.16)可知式子(3.1)具有唯一性。
,必有一个变大一个变小,由(3.16)可知式子(3.1)具有唯一性。
当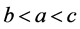 时,
时, 有下列的关系式子
有下列的关系式子
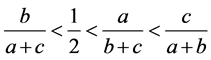 或者
或者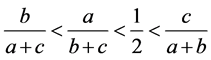 (3.17)
(3.17)
同样式子 ,必有一个变大一个变小,由(3.17)可知式子(3.1)具有唯一性。
,必有一个变大一个变小,由(3.17)可知式子(3.1)具有唯一性。
当 时,
时,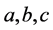 有下列的关系式子
有下列的关系式子
 或者
或者 (3.18)
(3.18)
同样可知式子 ,必有一个变大一个变小,由(3.18)可知式子(3.1)具有唯一性。
,必有一个变大一个变小,由(3.18)可知式子(3.1)具有唯一性。
当 时,
时,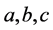 有下列的关系式子
有下列的关系式子
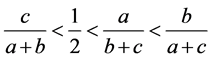 或者
或者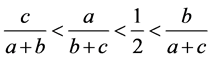 (3.19)
(3.19)
同样可知式子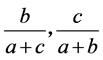 ,必有一个变大一个变小,由(3.19)可知式子(3.1)具有唯一性。
,必有一个变大一个变小,由(3.19)可知式子(3.1)具有唯一性。
当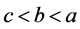 时,
时,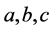 有下列的关系式子
有下列的关系式子
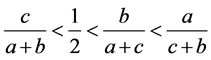 或者
或者 (3.20)
(3.20)
同样可知式子 ,必有一个变大一个变小,由(3.20)可知式子(3.1)具有唯一性,所以当
,必有一个变大一个变小,由(3.20)可知式子(3.1)具有唯一性,所以当 满足上述情况时其解具有唯一性,证毕。
满足上述情况时其解具有唯一性,证毕。
说明:在Case III中,我们并没有证明方程组(1.2)的唯一性,要证明其唯一性,我们还必须证明其(3.15)到(3.20)之间的不可能同时存在性。
证明:当单元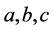 满足(3.15)到(3.20)时,
满足(3.15)到(3.20)时,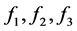 满足下面的关系
满足下面的关系
(1) 当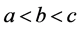 (1)时,有
(1)时,有
(2)当 时,有
时,有
(3) 当 时,有
时,有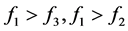
(4)当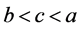 时,有
时,有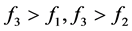
(5) 当 时,有
时,有
(6) 当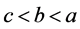 时,有
时,有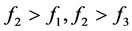
可知有(1)(6)≈(2)(4)≈(3)(5),这是三种情况,我们仅需证明其中一种即可说明理由,即有(1)(6)时,不可能有(2)(4)、(3)(5),于是仅需证明在(1)(6)情况下,方程组(1.2)不可能有两组解即可,首先证明当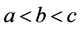 (1)时,有
(1)时,有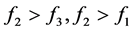 。
。
当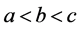 时,可知式子(3.15)成立,由(3.15)可知要分两种情况讨论,讨论如下:
时,可知式子(3.15)成立,由(3.15)可知要分两种情况讨论,讨论如下:
当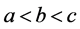 满足
满足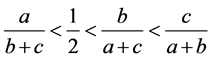 时,由均值不等式性质可知有
时,由均值不等式性质可知有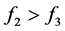 ,下面证明
,下面证明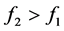 ,将
,将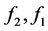 两式做差,如下
两式做差,如下
 (3.21)
(3.21)
有(3.21)可知
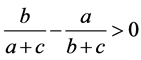 ,
,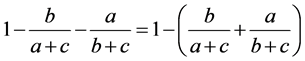
则有下面的不等式
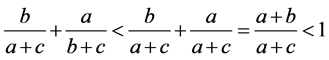
可知
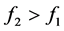
当 满足
满足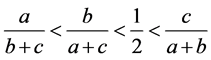 时,有均值不等式性质可知
时,有均值不等式性质可知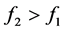 ,下面证明
,下面证明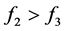 ,同样的道理做差则有下列式子
,同样的道理做差则有下列式子
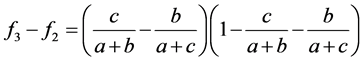 (3.22)
(3.22)
有(3.22)可知
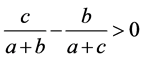 ,
,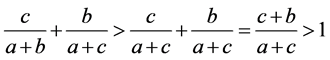
于是当 (1)时,有
(1)时,有 ,其他同里可证。
,其他同里可证。
由(1)(6),我们可以知道(1)(6)有下列的关系式子
当(1)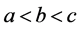 时,有
时,有 ,当(6)
,当(6)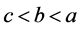 时,有
时,有 ,若此两种情况下有
,若此两种情况下有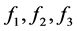 相等,则有下列的情况,由上面的证明以及其需要我们引入三个未知量
相等,则有下列的情况,由上面的证明以及其需要我们引入三个未知量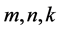 ,当
,当 ,使其满足下面的式子
,使其满足下面的式子
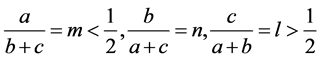 (3.23)
(3.23)
同理,当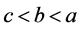 时,有下面的式子成立
时,有下面的式子成立
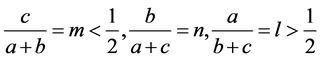 (3.24)
(3.24)
添加内容当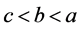 时,还存在下面的式子成立
时,还存在下面的式子成立
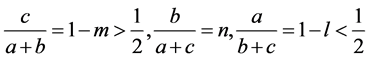 (3.25)
(3.25)
由(3.23)可以得到下面的式子成立
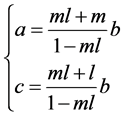 (3.26)
(3.26)
由(3.26)可得下面的式子
 (3.27)
(3.27)
同样有(3.25)可得下面的式子
 (3.28)
(3.28)
 (3.29)
(3.29)
由(3.27)(3.29)可知存在下面两种情况
(1) 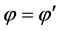 (2)
(2) 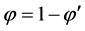
当(1)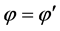 时,由其对称性可以得到
时,由其对称性可以得到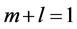 ,由
,由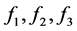 以及式子(3.1)可知此种情况不成立。
以及式子(3.1)可知此种情况不成立。
当(2) 时,可以得到下面的式子成立
时,可以得到下面的式子成立
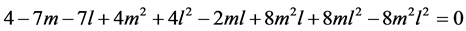 (3.30)
(3.30)
可知存在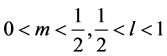 使式子(4.1)成立,故可能存在两个解使方程组(1.2)成立。
使式子(4.1)成立,故可能存在两个解使方程组(1.2)成立。
4. 方程组(1.2)存在两个解的构造的设想法
在这里主要由式子(3.30)去构造使方程组(1.2)存在两个解的方程组,即去构造一个 为常数的方程组(1.2)。
为常数的方程组(1.2)。
由式子(3.30)可以得到一组真实解关于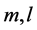 ,代入到(3.26)(3.28)可以得到两组关系式,分别记为(4.1)(4.2),为了区别这两种情况我们有下列标记:
,代入到(3.26)(3.28)可以得到两组关系式,分别记为(4.1)(4.2),为了区别这两种情况我们有下列标记:
当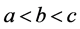 时,
时, 标记为
标记为 ,当
,当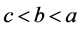 时,
时, ,标记为
,标记为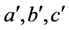 ,由方程组(1.2)可以得到下面的式子成立
,由方程组(1.2)可以得到下面的式子成立
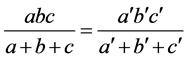 (4.3)
(4.3)
由式子(4.3)可以得到下面的式子成立
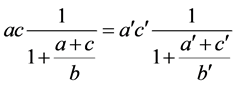 (4.4)
(4.4)
由(3.26)(3.27)(3.28)(3.29)以及(4.4)式以及 的真实解,可以得到一个式子
的真实解,可以得到一个式子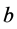 与
与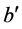 的关系式子,给
的关系式子,给 赋值便可得到一个
赋值便可得到一个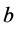 的值,由(3.26)(3.28)可以得到
的值,由(3.26)(3.28)可以得到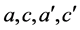 的值,即为方程组的两组解,将其代入到方程组(1.2)即可得到
的值,即为方程组的两组解,将其代入到方程组(1.2)即可得到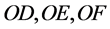 的值,那么就证明了方程组(1.2)可能存在两个解。此时由
的值,那么就证明了方程组(1.2)可能存在两个解。此时由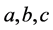 和
和 得到的两组
得到的两组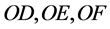 必然对应相等,请读者构造一个这样的三角行,所以方程组(1.2)在
必然对应相等,请读者构造一个这样的三角行,所以方程组(1.2)在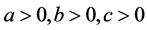 至多有两个解,作者曾用Matlab对方程组(1.2)做了大量的数据实验可知方程组(1.2)至多存在两解,有兴趣请参见中国预印本网站(893)。
至多有两个解,作者曾用Matlab对方程组(1.2)做了大量的数据实验可知方程组(1.2)至多存在两解,有兴趣请参见中国预印本网站(893)。
5. 方程组(1.1)在 的情况下解的判定
的情况下解的判定
首先,我们将要证明方程组(1.1)在 的情况下解的情况,同样令
的情况下解的情况,同样令 ,且假设单元
,且假设单元 满足
满足 ,则
,则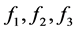 存在下面的关系
存在下面的关系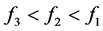 。在方程组(1.2)中,当单元
。在方程组(1.2)中,当单元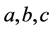 满足
满足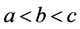 时,并不一定存在
时,并不一定存在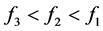 。故有如下定义,含有
。故有如下定义,含有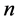 个单元的方程组,当这
个单元的方程组,当这 个单元具有一定的序列,即存在某种大小关系时,相应的
个单元具有一定的序列,即存在某种大小关系时,相应的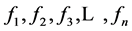 也存在某种相应的序列,即存在某种大小关系时,称这样的方程组为同化形方程组,同样当有
也存在某种相应的序列,即存在某种大小关系时,称这样的方程组为同化形方程组,同样当有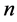 个单元的方程组,当这
个单元的方程组,当这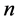 个单元具有一定的序列,即存在某种大小关系时,相应的
个单元具有一定的序列,即存在某种大小关系时,相应的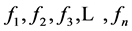 不存在某种相应的序列,即不存在某种大小关系时,称这样的方程组为异化形方程组,同样可以证明方程组(2.1)为同化形方程组。
不存在某种相应的序列,即不存在某种大小关系时,称这样的方程组为异化形方程组,同样可以证明方程组(2.1)为同化形方程组。
引理5.1:因为方程组(1.1)(1.3)为同化形方程组,所以在方程组(1.1)(1.3)中,当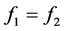 时必仅有
时必仅有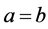 ,当
,当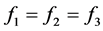 时,仅有
时,仅有 .
.
有引理5.1可知,我们仅需讨论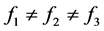 的情况。又因为方程组(1.1)是满足线性代数方程组,同样的做比值式,则有如下的形式
的情况。又因为方程组(1.1)是满足线性代数方程组,同样的做比值式,则有如下的形式
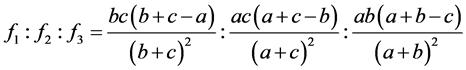 (5.1)
(5.1)
因为方程组(1.1)为拓扑对称方程组,故有引理2.1可知要进行下面的六种讨论
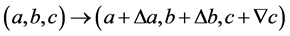 (2.12)
(2.12)
 (2.14)
(2.14)
 (2.19)
(2.19)
 (2.20)
(2.20)
 (2.21)
(2.21)
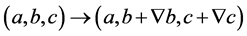 (2.22)
(2.22)
现就上面六种情况讨论如下
 (2.12)
(2.12)
式子(5.1)具有下面的变化(在上面的六种变化中,同样要保证单元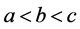 )
)

此时,用这种方法并不能证明在
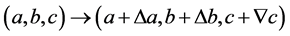 (2.12)
(2.12)
情况下,方程组仅有一解,于是我们弱化其结论,当
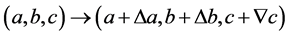 (2.12)
(2.12)
可知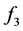 将要变大,令变化后的
将要变大,令变化后的 为
为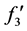 ,则
,则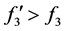 所以其弱化结论将要证明当
所以其弱化结论将要证明当
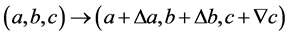 (2.12)
(2.12)
方程组仅有一解
当
 (2.14)
(2.14)
可知式子(5.1)有下面变化

同样在这种情况下,仅能弱化其结论,可知其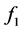 将要变小,所以其弱化结论将要证明当
将要变小,所以其弱化结论将要证明当
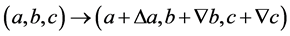 (2.14)
(2.14)
方程组仅有一解
当
 (2.20)
(2.20)
式子(5.1)具有下面的变化
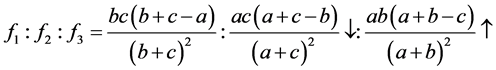
此时,可以证明在此情况下其解具有惟一性。
当
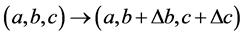 (2.19)
(2.19)
式子(5.1)具有下面的变化

令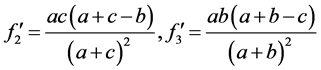 ,可知
,可知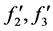 中也必有一个变大,同样要弱化其结论,可知
中也必有一个变大,同样要弱化其结论,可知 将要变大,而
将要变大,而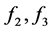 中也必有一个变大,故在弱化其结论情况下
中也必有一个变大,故在弱化其结论情况下
当
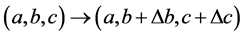 (2.19)
(2.19)
方程组仅有一解。
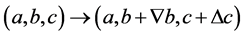 (2.21)
(2.21)
其式子(5.1)有下面的变化
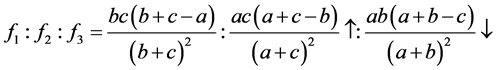
此时,可以证明在此情况下其解具有惟一性。
当
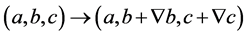 (2.22)
(2.22)
式子(5.1)有下面的变化
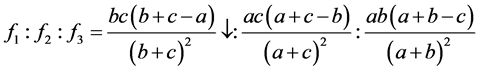
同样可知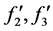 中也必有一个变小,同样要弱化其结论,可知
中也必有一个变小,同样要弱化其结论,可知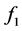 将要变小,而
将要变小,而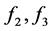 中也必有一个变小,故在弱化其结论情况下
中也必有一个变小,故在弱化其结论情况下
当
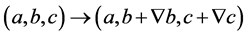 (2.22)
(2.22)
方程组仅有一解。
最后说明:为什么说是弱化结论,因为我们仅能证明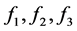 中的一个变大或变小,并不能保证其余两项中存在向相反的方向变化,故可能存在同向变化,即
中的一个变大或变小,并不能保证其余两项中存在向相反的方向变化,故可能存在同向变化,即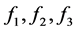 都变大,或都变小,此时,可能存在另一组
都变大,或都变小,此时,可能存在另一组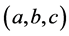 的解满足方程组(1.1),但是有上面的六种变化可知方程组(1.1)在
的解满足方程组(1.1),但是有上面的六种变化可知方程组(1.1)在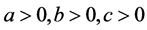 情况下至多有一解,用同样的方法可以证明方程组(1.3)在
情况下至多有一解,用同样的方法可以证明方程组(1.3)在 情况下至多有一解
情况下至多有一解
证毕。
6. 总结与展望
基于本文作者给出如下感兴趣的定义及猜想:在异化形方程组中,当这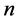 个单元具有一定的序列,即存在某种大小关系时,
个单元具有一定的序列,即存在某种大小关系时, 中可以确定其大小的表达式的个数定义为确数,如方程组(1.2)当假设单元
中可以确定其大小的表达式的个数定义为确数,如方程组(1.2)当假设单元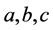 具有一定的大小关系时,在表达式
具有一定的大小关系时,在表达式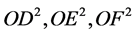 中可以确定一个数在三个中最大,而其余两个则无法判断其大小,为此确数为1,这种不能够确定其大小的表达式的个数定义为非确数。又如含有
中可以确定一个数在三个中最大,而其余两个则无法判断其大小,为此确数为1,这种不能够确定其大小的表达式的个数定义为非确数。又如含有 个单元的同化形方程组,可知其确数为
个单元的同化形方程组,可知其确数为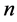 。为此有下面的猜想
。为此有下面的猜想
猜想1:含有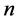 个单元的异化形拓扑对称方程组,在这
个单元的异化形拓扑对称方程组,在这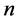 个单元都大于零时的方程组的解的最大个数为非确数。
个单元都大于零时的方程组的解的最大个数为非确数。
猜想2:含有 个单元的同化形拓扑对称方程组,在这
个单元的同化形拓扑对称方程组,在这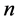 个单元都大于零时,方程组至多有一个解。
个单元都大于零时,方程组至多有一个解。
问题3:对于拓扑对称方程组, 之间的关系与方程组解的个数的关系(这里的解指单元大于零的解)。
之间的关系与方程组解的个数的关系(这里的解指单元大于零的解)。
问题4:能否将本文中的方法推广到一般的方程组上去,或者完成某种分类问题。
猜想5:此猜想是由猜想1,猜想2所延伸的猜想,对于含有三个单元的拓扑对称方程组,其解的个数(这里的解指单元大于零的解)至多为3。
猜想6:对于含有个 单元的拓扑对称方程组,其解的个数(这里的解指单元大于零的解)至多为
单元的拓扑对称方程组,其解的个数(这里的解指单元大于零的解)至多为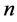 。
。
问题7:能否将本文应用在密码学领域。以上7个问题作为作者今后发展的方向。
参考文献 (References)
- [1] Zhou, Y.N. (2014) A kind of proof about triangles’s congruent and a new kind of elimination method. Open Science Repository Mathematics, open-access, e23050492.