Pure Mathematics
Vol.05 No.02(2015), Article ID:14912,4
pages
10.12677/PM.2015.52008
Partial Orders on U-Superabundant Semigroups
Yanan Yang, Xueming Ren
School of Science, Xi’an University of Architecture & Technology, Xi’an Shaanxi
Email: 376548195@qq.com
Received: Feb. 18th, 2015; accepted: Feb. 27th, 2015; published: Mar. 5th, 2015
Copyright © 2015 by authors and Hans Publishers Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/



ABSTRACT
The partial orders 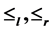 and
and 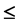 on U-superabundant semigroups
on U-superabundant semigroups  are defined. It is pro- ved that the partial order
are defined. It is pro- ved that the partial order  about the multiplication on
about the multiplication on  is compatible if and only if that the U-superabundant semigroups
is compatible if and only if that the U-superabundant semigroups 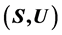 is a locally generalized Clifford semigroup.
is a locally generalized Clifford semigroup.
Keywords:U-Superabundant Semigroups, Partical Order, Compatiblility, Generalized Clifford Semigroup

U-超富足半群上的偏序
杨亚楠,任学明
西安建筑科技大学理学院,陕西 西安
Email: 376548195@qq.com
收稿日期:2015年2月18日;录用日期:2015年2月27日;发布日期:2015年3月5日

摘 要
定义了U-超富足半群 上的偏序
上的偏序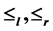 及£。证明了偏序
及£。证明了偏序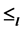 关于
关于 上的乘法是相容的,当且仅当
上的乘法是相容的,当且仅当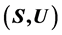 为局部广义Clifford半群。
为局部广义Clifford半群。
关键词 :U-超富足半群,偏序,相容性,广义Clifford半群

1. 引言
令S为一半群,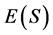 为S的幂等元集合.取定
为S的幂等元集合.取定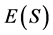 的一个非空子集U,称其为S的投射元集。由Lawson的文献[1] ,半群S上的关系
的一个非空子集U,称其为S的投射元集。由Lawson的文献[1] ,半群S上的关系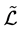 和
和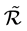 分别定义如下:
分别定义如下:

易知,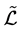 ,
,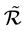 均为S上的等价关系。它们的交
均为S上的等价关系。它们的交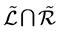 用
用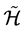 来表示,它们的连
来表示,它们的连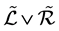 用
用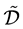 来表示。易证
来表示。易证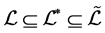 ,
, 。据文献[2] 知,当S为正则半群时,
。据文献[2] 知,当S为正则半群时, ,
,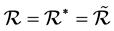 。
。
若半群S的每一个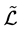 类和每一个
类和每一个 类都含有U中的元素,则称U-半群S为半富足半群。若U-半富足半群S满足同余条件,即
类都含有U中的元素,则称U-半群S为半富足半群。若U-半富足半群S满足同余条件,即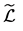 为S上的右同余,
为S上的右同余,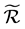 为S上的左同余,则称S为富足半群。每一个
为S上的左同余,则称S为富足半群。每一个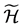 类都含有U中的元素的U-富足半群,称其为U-超富足半群,记为
类都含有U中的元素的U-富足半群,称其为U-超富足半群,记为 。易知,完全正则半群,超富足半群都是U-超富足半群。
。易知,完全正则半群,超富足半群都是U-超富足半群。
2. 准备知识
令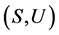 为U-超富足半群,且
为U-超富足半群,且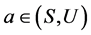 。本文总记元素a所在的
。本文总记元素a所在的 -类的U中的元素为
-类的U中的元素为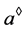 。
。 为由a生成的最小U允许左理想;对偶地,
为由a生成的最小U允许左理想;对偶地,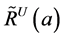 为由a生成的最小U允许右理想。本文将主要研究U-超富足半群
为由a生成的最小U允许右理想。本文将主要研究U-超富足半群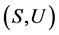 上的几个偏序。我们先给出以下几个引理。
上的几个偏序。我们先给出以下几个引理。
引理1 [3] 在U-超富足半群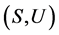 中,令
中,令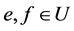 ,则有
,则有
(1)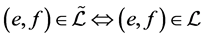 ;
;
(2) 。
。
引理2 [4] 令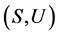 为U-超富足半群,且
为U-超富足半群,且 。若
。若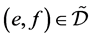 ,则
,则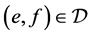 。
。
引理3 [4] 在U-超富足半群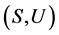 中,
中, 。
。
引理4 [4] 在U-超富足半群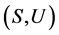 中,
中, 。
。
引理5 [4] 令S为半群,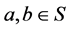 ,则
,则
(1)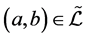 ,当且仅当
,当且仅当 ;
;
(2)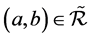 ,当且仅当
,当且仅当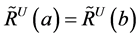 。
。
推论6 令S为半群,对任意的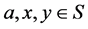 ,则
,则
(1)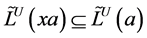 ;
;
(2)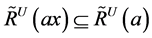 。
。
证明 (1) 因 是包含a的S的一个左理想,而
是包含a的S的一个左理想,而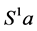 是包含a的最小左理想,故
是包含a的最小左理想,故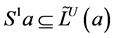 。于是,
。于是,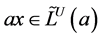 。这就证明了
。这就证明了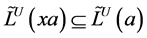 。
。
类似地,我们可以证明(2)。
引理7 [4] 在U-超富足半群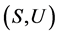 中,若
中,若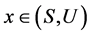 ,
,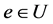 ,则下列两款成立:
,则下列两款成立:
(1)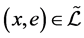 ,当且仅当对于任意
,当且仅当对于任意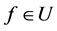 ,
, 。特别地,
。特别地,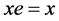 。
。
(2)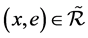 ,当且仅当对于任意
,当且仅当对于任意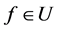 ,
,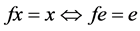 。特别地,
。特别地,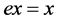 。
。
引理8 [5] 令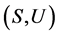 为U-超富足半群,
为U-超富足半群,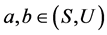 。若
。若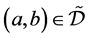 ,则
,则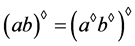 。
。
3. 主要结果及证明
首先,回忆在半群S的幂等元集 上的两个前序
上的两个前序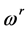 和
和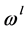 。
。
令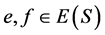 ,如下定义前序
,如下定义前序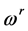 与
与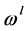 :
:
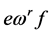 ,当且仅当
,当且仅当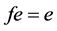 ;
;
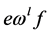 ,当且仅当
,当且仅当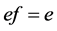 ;
;
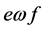 ,当且仅当
,当且仅当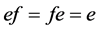 。
。
现在,我们给出U-超富足半群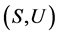 上的几个偏序的定义。
上的几个偏序的定义。
定义1 令 为U-超富足半群,则关于任意
为U-超富足半群,则关于任意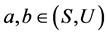 ,
,
(1)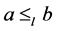 ,当且仅当
,当且仅当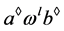 且
且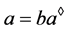 ;
;
(2)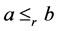 ,当且仅当
,当且仅当 且
且 ;
;
(3)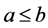 ,当且仅当
,当且仅当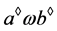 且
且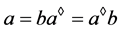 。
。
定理2 令 为U-超富足半群,则
为U-超富足半群,则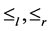 及
及 均为
均为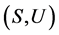 上的偏序。
上的偏序。
证明 我们只需证明定义1(1),类似地可证明(2),由(1)及(2),即可得(3)。
自反性。令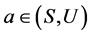 ,因
,因 为U-超富足半群,则
为U-超富足半群,则 ,由引理7,有
,由引理7,有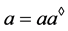 ,又由
,又由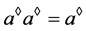 ,即
,即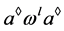 ,故
,故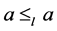 。
。
反对称性。令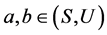 ,
,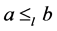 且
且 。则由定义1(1)得,
。则由定义1(1)得,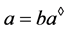 ,
, 且
且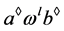 ,即
,即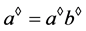 。注意到
。注意到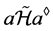 ,则
,则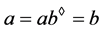 。
。
传递性。令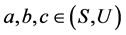 ,
,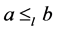 且
且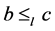 ,则由定义1(1)得,
,则由定义1(1)得,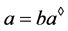 ,
,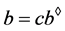 且
且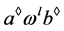 ,
, 。则
。则 ,
,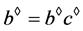 ,注意到,
,注意到,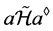 ,
, ,则
,则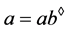 ,
,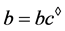 ,因此,
,因此,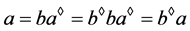 ,注意到
,注意到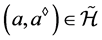 ,故
,故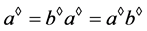 ,类似可得,
,类似可得,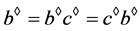 ,故
,故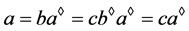 ,
, ,注意到
,注意到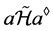 ,则
,则 ,即
,即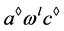 ,因此
,因此 。
。
命题3 令 为U-超富足半群,
为U-超富足半群,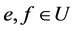 且
且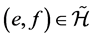 ,则
,则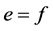 。
。
证明 因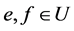 ,且
,且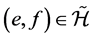 ,则
,则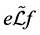 且
且 。由引理1可得,
。由引理1可得, 且
且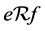 ,即
,即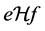 ,则
,则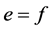 。
。
命题4 令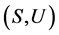 为U-超富足半群,
为U-超富足半群,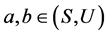 且
且 ,若
,若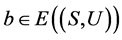 ,则
,则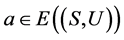 。
。
证明 据定义1(1),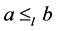 ,当且仅当
,当且仅当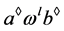 且
且 。由假设,若
。由假设,若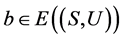 ,注意到
,注意到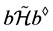 ,由命题3,则
,由命题3,则 。从而
。从而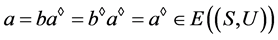 。
。
半群S上的关系r称为左相容的,若关于任意 ,
,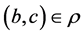 蕴涵
蕴涵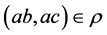 ,对偶地,可有r为右相容的,半群S上的关系r称为相容的,如果r既为左相容的,又为右相容的。
,对偶地,可有r为右相容的,半群S上的关系r称为相容的,如果r既为左相容的,又为右相容的。
定义5 完全正则半群S称为Clifford半群,若S中每个幂等元都是可交换的。
定义6 U-富足半群S称为广义Clifford半群,若S中每个投射元都在S的中心里。
定义7 半群S称为局部P半群,若关于任意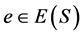 ,
,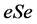 满足性质P。
满足性质P。
定理8 若 是U-超富足半群,则
是U-超富足半群,则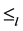 关于
关于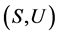 上的乘法是相容的,当且仅当
上的乘法是相容的,当且仅当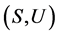 为局部广义Clifford半群。
为局部广义Clifford半群。
证明 必要性。首先,证明关于任意 ,
, 为
为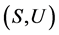 的一个子半群。
的一个子半群。
若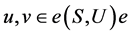 ,则存在
,则存在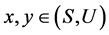 ,使得
,使得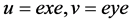 ,由此可得,
,由此可得,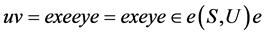 ,即
,即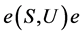 为
为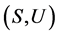 的一个子半群。
的一个子半群。
其次,容易验证,若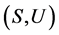 为U-超富足半群,则
为U-超富足半群,则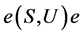 也为U-超富足半群。
也为U-超富足半群。
最后,若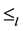 关于S上的乘法是相容的,则关于任意
关于S上的乘法是相容的,则关于任意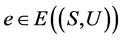 ,
,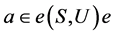 且
且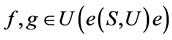 ,有
,有 及
及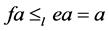 ,
, 。据命题3,可得
。据命题3,可得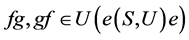 。注意到,
。注意到,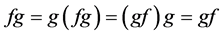 ,又若
,又若 ,则
,则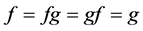 。若
。若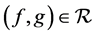 ,则
,则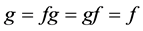 。
。
由文献[4] 知,在U-超富足半群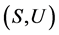 中,有
中,有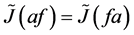 ,即
,即 。又因
。又因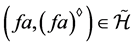 且
且 ,则
,则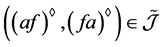 ,又据引理4得,
,又据引理4得,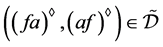 ,则据引理3,存在
,则据引理3,存在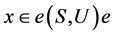 ,使得
,使得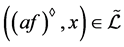 且
且 。注意到
。注意到 ,故
,故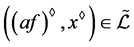 且
且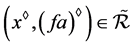 。因在正则条件下,
。因在正则条件下,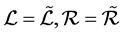 ,则
,则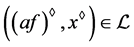 且
且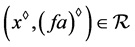 ,因此根据以上的推导,可得
,因此根据以上的推导,可得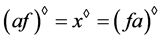 ,
,
又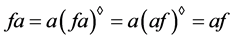 ,因此
,因此 中的投射元都在中心上。至此,我们证明了
中的投射元都在中心上。至此,我们证明了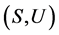 是一个局部广义Clifford半群。
是一个局部广义Clifford半群。
充分性。首先,证明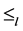 关于
关于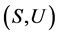 上的乘法是左相容的。
上的乘法是左相容的。
令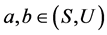 且
且 ,由定义1(1)知,
,由定义1(1)知,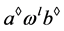 ,
,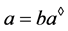 。则
。则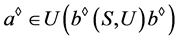 ,且关于任意
,且关于任意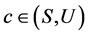 ,有
,有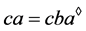 。因
。因 且
且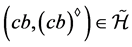 ,则
,则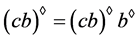 。由此可得
。由此可得
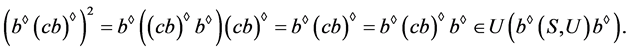
从而,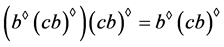 且
且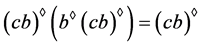 ,因此
,因此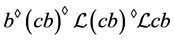 。注意到
。注意到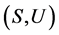 为局部广义Clifford半群,
为局部广义Clifford半群,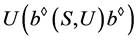 为一个半格,则我们可得
为一个半格,则我们可得
(a)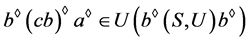 ;
;
(b)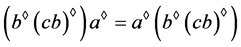 ;
;
(c)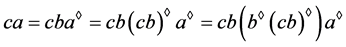 ;
;
(d) 。
。
据引理5及推论6,可得
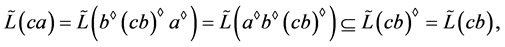
因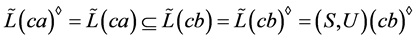 ,故存在
,故存在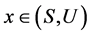 ,使得
,使得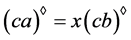 。因此
。因此 ,另外,由(a),(d)及命题3得,
,另外,由(a),(d)及命题3得,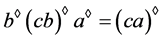 ,则有,
,则有,
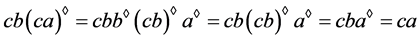 .
.
因此,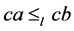 。即
。即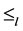 关于
关于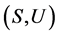 上乘法是左相容的。
上乘法是左相容的。
下证, 关于
关于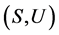 上的乘法是右相容的。
上的乘法是右相容的。
令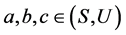 ,且
,且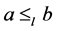 ,则
,则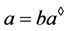 ,从而
,从而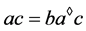 ,注意到
,注意到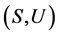 为U-超富足半群,则有
为U-超富足半群,则有
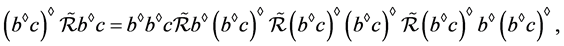
则可得到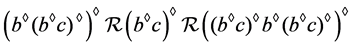 ,且注意到
,且注意到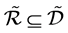 ,则有
,则有
 .
.
据引理8,可得,
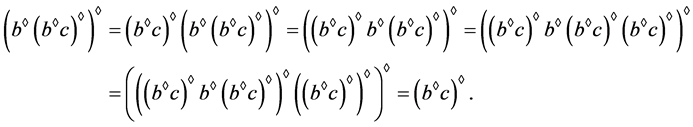
从而,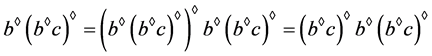 。
。
因此,可得
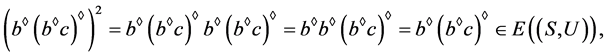
且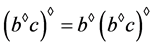 。这蕴含着
。这蕴含着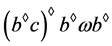 ,由此可得
,由此可得
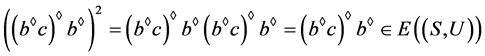 。
。
从而,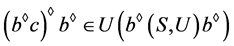 ,注意到
,注意到 ,
,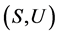 为局部广义Clifford半群且
为局部广义Clifford半群且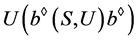 为一个半格,有
为一个半格,有
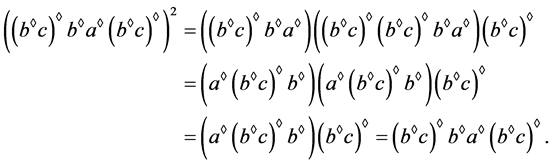
易知, 。令
。令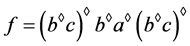 ,则
,则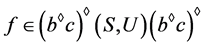 且
且 。因为
。因为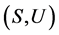 为局部广义Clifford半群,有
为局部广义Clifford半群,有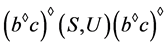 为广义Clifford半群,从而可得
为广义Clifford半群,从而可得
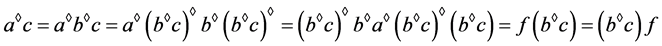 。
。
注意到, 且
且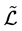 为
为 上的右同余,则可得
上的右同余,则可得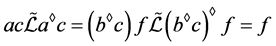 ,从而可得
,从而可得
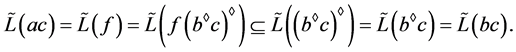
由左相容性的证明过程可知,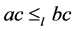 ,即
,即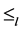 关于
关于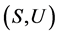 上乘法是右相容的。
上乘法是右相容的。
至此,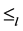 关于
关于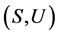 上乘法是相容的得到了证明。
上乘法是相容的得到了证明。
基金项目
国家自然科学基金项目(批准号:11471255)。
文章引用
杨亚楠,任学明, (2015) U-超富足半群上的偏序
Partial Orders on U-Superabundant Semigroups. 理论数学,02,54-58. doi: 10.12677/PM.2015.52008
参考文献 (References)
- 1. Lawson, M.V. (1990) Rees matrix semigroups. Proceedings of the Edinburgh Mathematical Society, 33, 23-37.
- 2. Petrich, M. and Reilly, N.R. (1999) Completely regular semigroups. New York, John Wiley & Sons.
- 3. Lawson, M.V. (1991). Semigroups and ordered categories. I. the reduced case. Journal of Algebra, 141, 422-462.
- 4. 任学明, 岑嘉评, 郭聿琦 (2009) 半群的广义Clifford定理.中国科学(A辑), 10, 1211-1215.
- 5. Qiu, X.W., Guo, X.J. and Shum, K.P. (2013) Strongly rpp semigroups endowed with some natural partial orders. Journal of Semigroup Theory and Applications, 7, 2051-2937.