Pure Mathematics
Vol.05 No.03(2015), Article ID:15366,9
pages
10.12677/PM.2015.53018
The Extreme Points and Rotundity of Orlicz-Sobolev Spaces
Fayun Cao
College of Sciences, Shanghai University, Shanghai
Email: caofayun@126.com
Received: May 7th, 2015; accepted: May 22nd, 2015; published: May 29th, 2015
Copyright © 2015 by author and Hans Publishers Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/



ABSTRACT
In this paper we give a modular norm for Orlicz-Sobolev spaces, and obtain a necessary and sufficient condition for the Orlicz-Sobolev spaces which is formed by strictly convex N function to be rotund.
Keywords:Orlicz-Sobolev Spaces, Extreme Points, Rotund, Modular Norm
Orlicz-Sobolev空间的端点与严格凸性
曹法赟
上海大学理学院,上海
Email: caofayun@126.com
收稿日期:2015年5月7日;录用日期:2015年5月22日;发布日期:2015年5月29日

摘 要
本文在Orlicz-Sobolev空间上给出了一种模范数,给出了由严格凸N函数生成Orlicz-Sobolev空间严格凸的充要条件。
关键词 :Olicz-Sobolev空间,端点,严格凸,模范数

1. 引言
Orlicz空间是泛函分析的一个重要分支,它深入地研究了比熟知的 空间更加广泛的一类空间,Sobolev空间是20世纪初形成的有着重要价值的数学模型,在方程理论有着重要的应用价值,Orlicz-Sobolev空间则是Sobolev空间的重要推广,Orlicz-Sobolev空间的发展不仅完善了Banach空间理论,而且为解决实际问题提供了丰富的模型。空间的严格凸性在最佳逼近和最优化控制等领域有着直接的应用。所以研究Orlicz-Sobolev空间的严格凸性有着深远的意义。本文在Orlicz-Sobolev空间上给出了一种模范数,得到了摸与范数的关系式。给出了了由严格凸N函数生成的Orlicz-Sobolev空间严格凸的充要条件。2001年,陈述涛和胡长英[1] 给出了Orlicz-Sobolev空间关于Luxemburg范数的端点和严格凸的充要条件,但是文章中已经假定
空间更加广泛的一类空间,Sobolev空间是20世纪初形成的有着重要价值的数学模型,在方程理论有着重要的应用价值,Orlicz-Sobolev空间则是Sobolev空间的重要推广,Orlicz-Sobolev空间的发展不仅完善了Banach空间理论,而且为解决实际问题提供了丰富的模型。空间的严格凸性在最佳逼近和最优化控制等领域有着直接的应用。所以研究Orlicz-Sobolev空间的严格凸性有着深远的意义。本文在Orlicz-Sobolev空间上给出了一种模范数,得到了摸与范数的关系式。给出了了由严格凸N函数生成的Orlicz-Sobolev空间严格凸的充要条件。2001年,陈述涛和胡长英[1] 给出了Orlicz-Sobolev空间关于Luxemburg范数的端点和严格凸的充要条件,但是文章中已经假定 满足
满足 条件,同年二人 [2] 讨论Orlicz-Sobolev空间关于最大值范数的端点和严格凸的性质,但未对空间严格凸的充要条件进行深入讨论,本文给出了一种新的Luxemburg范数,在此范数形成的Orlicz-Sobolev空间与Orlicz有着很多平行的性质,可以用研究Orlicz空间的方法来研究Orlicz-Sobolev空间。
条件,同年二人 [2] 讨论Orlicz-Sobolev空间关于最大值范数的端点和严格凸的性质,但未对空间严格凸的充要条件进行深入讨论,本文给出了一种新的Luxemburg范数,在此范数形成的Orlicz-Sobolev空间与Orlicz有着很多平行的性质,可以用研究Orlicz空间的方法来研究Orlicz-Sobolev空间。
2. 预备知识
定义 1 [3] :函数 为
为 函数是指
函数是指 满足如下条件:
满足如下条件:
1) 为偶的,连续的,凸函数且
为偶的,连续的,凸函数且 ;
;
2) 当时 时,
时, ;
;
3) ,
, 。
。
若还有: ,有
,有 则称
则称 是严格凸的。
是严格凸的。
用 表示
表示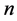 维Euclid空间
维Euclid空间 中的有界集,
中的有界集, 是定义在
是定义在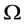 上Lebesgue可测函数,
上Lebesgue可测函数,


 ,
, 是
是 的线性子空间,在
的线性子空间,在 上定义如下实值函数:
上定义如下实值函数:
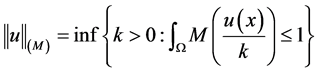
则 为Banach空间。
为Banach空间。
定义2 [4] :称 在区间
在区间 仿射是指:
仿射是指: 使得
使得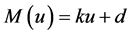 ,
, 。
。
定义3 [4] : 是指:
是指: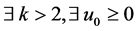 ,满足:
,满足:

若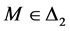 则有
则有 。
。
定义4 [4] :设 为
为 函数,
函数, ,若
,若 且
且 ,则有
,则有 ,就称
,就称 为
为 的严格凸点,其严格凸点全体记为
的严格凸点,其严格凸点全体记为 。
。
定义5 [5] :设 是Banach空间,
是Banach空间, 是其单位闭球,
是其单位闭球, 为单位球面,
为单位球面, ,若
,若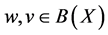 ,且
,且 ,则有
,则有 就称
就称 为
为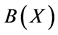 的端点,其端点的全体记为
的端点,其端点的全体记为 ,若有
,若有 ,则称
,则称 是严格凸空间。
是严格凸空间。
定义6 [6] :设 为
为 函数,
函数, 是
是 中有界连通开集,定义如下集合:
中有界连通开集,定义如下集合:

其中 为
为 的
的 阶弱导数,则
阶弱导数,则 为
为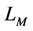 的线性子空间,在
的线性子空间,在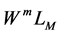 上定义如下两实值函数:
上定义如下两实值函数:

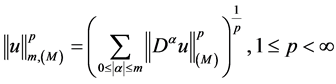
则 ,
, 均是Banach空间。
均是Banach空间。
3. 主要结果
定理1 设 为
为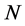 函数,
函数, 为
为 中有界连通开集,在
中有界连通开集,在 上定义如下实值函数:
上定义如下实值函数:

则 为Banach空间。
为Banach空间。
证明:容易证明 是
是 上的范数,记
上的范数,记 为满足
为满足 的
的 个数,
个数, ,下面证明
,下面证明 与
与 等价,因为
等价,因为

所以 ,另一方面
,另一方面

从而有 ,故两者等价,故
,故两者等价,故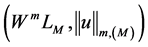 为Banach空间。
为Banach空间。
定理2 设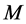 为
为 函数,
函数, 为
为 中有界连通开集,设
中有界连通开集,设 则有:
则有:
1) 若 ,则
,则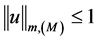 ;
;
2)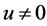 ,则
,则 ;
;
3) 若 ,则
,则 ;
;
4) 若 ,则
,则 。
。
证明:1) 由 的定义容易证明。
的定义容易证明。
2) 由 的定义知
的定义知 ,使得
,使得 ,且有如下三条性质:
,且有如下三条性质:
①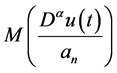 非负可测,
非负可测,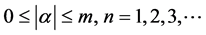
② ,
,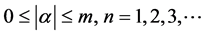
③ 
由Levy定理可知: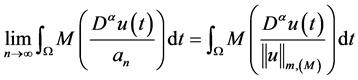 ,所以有:
,所以有:

即 ,所以
,所以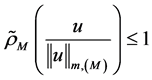 。
。
3) ,则
,则 ,则3)成立;
,则3)成立;
 ,由
,由 的凸性可知:
的凸性可知:

从而 。
。
4) 因为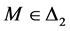 所以
所以 ,故
,故 关于
关于 在
在 上连续,于是
上连续,于是 关于
关于 在
在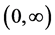 上连续,对于
上连续,对于 ,有
,有 ,结合3)可得
,结合3)可得

定理3 设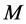 为
为 函数,
函数, 为
为 中有界连通开集,
中有界连通开集, 若有:
若有:
1) 
2) 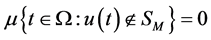
则
证明:设 由定理2知
由定理2知
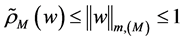 ,由
,由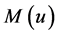 的凸性可知:
的凸性可知:
 (1)
(1)

从而以上不等式中各项均相等,所以
 (2)
(2)
结合(1) (2)得:
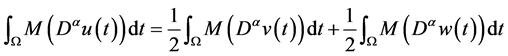
特别地当 时
时

再由 得
得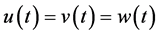 a.e on
a.e on ,所以
,所以 。
。
定理4 为
为 函数,
函数, 为
为 中有界连通开集,
中有界连通开集, 。若存在
。若存在 以及
以及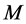 的仿射区间
的仿射区间 满足:
满足:

则
证明:记 ,由于
,由于 内部非空所以取
内部非空所以取 ,使得
,使得 ,
, ,并且
,并且 。
。
定义如下两个函数:


则 ,
, 令:
令:


 且
且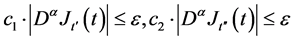 ,
, ,取
,取 。
。
定义如下函数:

则 ,
, ,
, 。
。
令 在
在 上为:
上为:

则:

所以 ,同理可得
,同理可得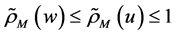 由定理2知
由定理2知 ,再由
,再由 可知
可知 。
。
定理5 设 为严格凸
为严格凸 函数,
函数, 为
为 中有界连通开方体,则
中有界连通开方体,则
 严格凸的充要条件是
严格凸的充要条件是 。
。
证明 充分性:结合定理3与定理2的4)可证得。
必要性:假设 则存在
则存在 ,使得
,使得

令 不妨设
不妨设 ,取
,取 :
: 和
和 满足:
满足: ,取
,取 和
和 使得
使得 ,依次可取得
,依次可取得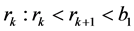 和
和 满足
满足 ,
, ,显然有
,显然有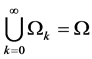 并且当
并且当 时
时 ,令
,令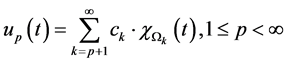 则:
则:

所以
 ,
, 使得
使得 从而:
从而:

由 的定义可知
的定义可知 ,由
,由 的任意性知
的任意性知 ,所以
,所以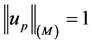 。
。
取 ,当
,当 时,有
时,有
取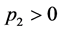 ,当
,当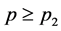 时,有
时,有

令



则


当 时
时

而





从而 有
有


从而 。又因为:
。又因为:

所以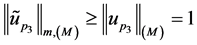 ,故
,故 。
。
令 ,
,

当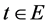 时
时

取 ,使得
,使得 ,
, ,
, ,且
,且
 。
。
定义如下两个函数:

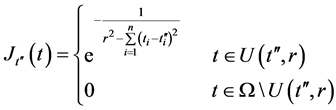
则 令:
令:
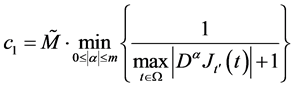

 且
且 ,
, ,取
,取 ,定义如下函数:
,定义如下函数:

则 ,
, ,
, 。
。
所以:
即 ,同理得
,同理得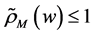 ,所以
,所以 ,而
,而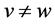 ,所以
,所以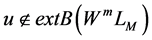 ,这与
,这与 严格凸相矛盾所以假设不成立,故
严格凸相矛盾所以假设不成立,故 。
。
推论1 设 为严格凸
为严格凸 函数,
函数, 为
为 中有界连通开方体,则
中有界连通开方体,则
 当且仅当
当且仅当 。
。
文章引用
曹法赟, (2015) Orlicz-Sobolev空间的端点与严格凸性
The Extreme Points and Rotundity of Orlicz-Sobolev Spaces. 理论数学,03,111-120. doi: 10.12677/PM.2015.53018
参考文献 (References)
- 1. 陈述涛, 胡长英 (2001) Orlicz-sobolev空间关于Luxemburg范数的端点与严格凸性. 哈尔滨师范大学自然科学学报, 2, 1-6.
- 2. 胡长英, 陈述涛 (2001) Orlicz-sobolev空间关于最大值范数的端点. 黑龙江大学自然科学学报, 4, 14-16.
- 3. 吴从忻 (1983) 奥尔里奇空间. 黑龙江科学技术出版社, 哈尔滨.
- 4. Chen, S.T. (1996) Geometry of Orlicz spaces. Polish Scientific Publisher, Warszawa, 356: 1-204.
- 5. 定光桂 (1984) 巴拿赫空间引论. 科学出版社, 北京.
- 6. Adams, R.A. (1983) Sobolev. 人民教育出版社, 北京.