Pure Mathematics
Vol.05 No.04(2015), Article ID:15728,5
pages
10.12677/PM.2015.54023
A Characterization for Locally Projectively Flat Berwald Type (α, β)-Metrics
Changtao Yu
School of Mathematical Sciences, South China Normal University, Guangzhou Guangdong
Email: yct9858@sohu.com
Received: Jul. 4th, 2015; accepted: Jul 16th, 2015; published: Jul. 22nd, 2015
Copyright © 2015 by author and Hans Publishers Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/



ABSTRACT
Berwald type  -metrics are those Finsler metrics expressed as
-metrics are those Finsler metrics expressed as , where
, where  is a Riemannian metric, and
is a Riemannian metric, and  is a 1-form. In this paper, by using a special deformations for
is a 1-form. In this paper, by using a special deformations for  and
and  due to
due to , we provide a characterization for locally projectively flat Berwald tpye
, we provide a characterization for locally projectively flat Berwald tpye  -metrics. Our characterization is simpler than the corresponding results of other researchers. Moreover, the geometrical structure of locally projectively flat Berwald type
-metrics. Our characterization is simpler than the corresponding results of other researchers. Moreover, the geometrical structure of locally projectively flat Berwald type  -metrics is much clearer.
-metrics is much clearer.
Keywords:Finsler Geometry,  -Metrics, Projective Flatness
-Metrics, Projective Flatness

局部射影平坦Berwald型(α, β)度量的一个刻画
余昌涛
华南师范大学数学科学学院,广东 广州
Email: yct9858@sohu.com
收稿日期:2015年7月4日;录用日期:2015年7月16日;发布日期:2015年7月22日

摘 要
Berwald型 度量是形如
度量是形如 的芬斯勒度量,其中
的芬斯勒度量,其中 是一个黎曼度量,
是一个黎曼度量, 是一个1形式。本文利用
是一个1形式。本文利用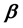 对
对 和
和 做一种特殊的度量形变,由此可以得到局部射影平坦Berwald型
做一种特殊的度量形变,由此可以得到局部射影平坦Berwald型 度量的一个刻画。该刻画不仅比其他研究者的相应方法和结论简单,而且从中我们可以看到局部射影平坦Berwald型
度量的一个刻画。该刻画不仅比其他研究者的相应方法和结论简单,而且从中我们可以看到局部射影平坦Berwald型 度量更为明确的几何结构。
度量更为明确的几何结构。
关键词 :芬斯勒几何,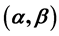 度量,射影平坦
度量,射影平坦

1. 引言
1900年,希尔伯特提出了23个数学问题,其中第四问题是求解所有以直线段为连接两点的最短路径的距离函数。在光滑情形下,希尔伯特第四问题便是求解所有欧氏空间的开集上以直线段为测地线的芬斯勒度量,具有这种性质的芬斯勒度量被称为是射影平坦的[1] 。芬斯勒度量是比黎曼度量更广泛的一类度量,它取消了对范数是二次型的限制[2] 。
有一些芬斯勒度量和黎曼度量比较接近,如Randers度量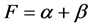 是由一个黎曼度量
是由一个黎曼度量 和一个1形式
和一个1形式 相加而得到的[3] 。而比Randers度量更一般的一类度量具有
相加而得到的[3] 。而比Randers度量更一般的一类度量具有 的形式,其中
的形式,其中 是一个光滑函数。这类度量被称为
是一个光滑函数。这类度量被称为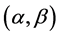 度量[4] 。当
度量[4] 。当 ,相应的
,相应的 度量便是Randers度量。
度量便是Randers度量。 度量具有良好的可计算性的特点,且其性质和黎曼度量比较接近,这使得对于这类度量的研究极大地丰富和发展了芬斯勒几何的相关领域。
度量具有良好的可计算性的特点,且其性质和黎曼度量比较接近,这使得对于这类度量的研究极大地丰富和发展了芬斯勒几何的相关领域。
1929年,Berwald构造了一个芬斯勒度量如下,
 ,
,
这个度量是单位球体 上具有常旗曲率
上具有常旗曲率 且测地线全为直线段的芬斯勒度量[5] 。其中,旗曲率是黎曼几何中截面曲率的自然推广,刻画了芬斯勒流形在一个点附近的弯曲程度[2] 。如果取黎曼度量
且测地线全为直线段的芬斯勒度量[5] 。其中,旗曲率是黎曼几何中截面曲率的自然推广,刻画了芬斯勒流形在一个点附近的弯曲程度[2] 。如果取黎曼度量 和1形式
和1形式 如下,
如下,
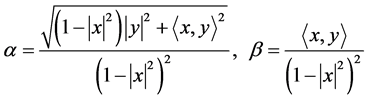 ,
,
则上述度量 可表示为
可表示为
 ,
,
这类度量现在被称为Berwald型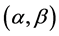 度量或平方型
度量或平方型 度量[6] 。
度量[6] 。
Berwald型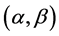 度量是一类特殊而重要的芬斯勒度量,它是除了Randers度量以外另一类具有良好几何性质的
度量是一类特殊而重要的芬斯勒度量,它是除了Randers度量以外另一类具有良好几何性质的 度量。关于Berwald型
度量。关于Berwald型 度量已经有不少结果。例如,2007年,B.Li和Z.Shen证明了,若
度量已经有不少结果。例如,2007年,B.Li和Z.Shen证明了,若 是一个局部射影平坦且具有常截面曲率的
是一个局部射影平坦且具有常截面曲率的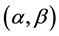 度量,则除了局部闵可夫斯基度量以外,
度量,则除了局部闵可夫斯基度量以外, 或者是Randers型度量,或者是Berwald型度量[7] 。2011年,L.Zhou进一步证明了,若Berwald型度量具有常旗曲率,则它必定是局部射影平坦的[8] 。2014年,Z.Shen和作者给出了Berwald型
或者是Randers型度量,或者是Berwald型度量[7] 。2011年,L.Zhou进一步证明了,若Berwald型度量具有常旗曲率,则它必定是局部射影平坦的[8] 。2014年,Z.Shen和作者给出了Berwald型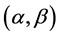 度量是爱因斯坦度量的一个简洁刻画[9] -[11] 。
度量是爱因斯坦度量的一个简洁刻画[9] -[11] 。
2. 预备知识
定义2.1 [1] :设 是一个
是一个 维光滑流形,是
维光滑流形,是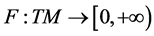 其切丛上的非负函数。如果
其切丛上的非负函数。如果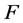 满足如下条件:
满足如下条件:
(1) 正齐性: ;
;
(2) 光滑性:在带孔切丛 上
上 是
是 函数;
函数;
(3) 正则性:对于任意非零向量 ,
,

构成正定的矩阵,则称 是
是 上的一个芬斯勒度量。
上的一个芬斯勒度量。
定义2.2 [1] :设 是
是 维光滑流形
维光滑流形 上的一个芬斯勒度量。如果对于
上的一个芬斯勒度量。如果对于 上的任意一点
上的任意一点 ,均存在
,均存在 的某个局部坐标系
的某个局部坐标系 ,使得在该坐标系下
,使得在该坐标系下 的所有测地线均为直线,则称
的所有测地线均为直线,则称 是局部射影平坦的芬斯勒度量。
是局部射影平坦的芬斯勒度量。
一个基本的结论是,如果 是局部射影平坦的芬斯勒度量,则在上述局部坐标系
是局部射影平坦的芬斯勒度量,则在上述局部坐标系 下,
下,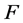 的测地系数
的测地系数 可表示为
可表示为
 ,
,
其中 是切丛
是切丛 上的标量函数,反之亦然[4] 。若
上的标量函数,反之亦然[4] 。若 是一个黎曼度量,则其测地系数
是一个黎曼度量,则其测地系数 可由其黎曼联络系数给出,即
可由其黎曼联络系数给出,即 。黎曼联络系数
。黎曼联络系数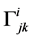 可利用下式确定:
可利用下式确定:
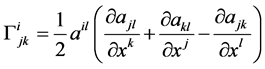 。
。
设 是一个光滑的正值函数,
是一个光滑的正值函数, 是开集
是开集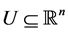 上的黎曼函数,
上的黎曼函数,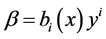 是满足模长
是满足模长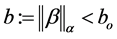 的1形式。则形如
的1形式。则形如

的芬斯勒度量称为 度量[4] 。
度量[4] 。
引理2.3 [4] :由上式确定的非负函数 是一个芬斯勒度量的充分必要条件是函数
是一个芬斯勒度量的充分必要条件是函数 满足
满足
 ,
,
其中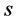 和
和 是满足
是满足 的任意实数。
的任意实数。
由上述引理易得下面的结果:
引理2.4 [4] : 是芬斯勒度量的充分必要条件是
是芬斯勒度量的充分必要条件是 。
。
3. 主要结果
利用经典的有理项无理项分离技巧,Z. Shen and G. C.Yildirim证明了如下结论:
定理3.1 [12] :设 是开集
是开集 上的芬斯勒度量。则
上的芬斯勒度量。则 是射影平坦的,当且仅当
是射影平坦的,当且仅当
 (1)
(1)
 (2)
(2)
其中 是
是 上的函数,
上的函数, 是
是 上的1形式。
上的1形式。
在此基础上,X. Mo, Z. Shen和C. Yang得到了如下的结论:
定理3.2 [6] :若Randers度量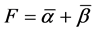 是局部射影平坦的,且具有迷向S曲率,则存在
是局部射影平坦的,且具有迷向S曲率,则存在 ,使得对于
,使得对于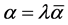 ,
, ,芬斯勒度量
,芬斯勒度量 是局部射影平坦的。
是局部射影平坦的。
在本文,我们将利用一种特殊的度量形变,给出不同于上述结果的另一种刻画。为此,我们先引入一些基本记号。我们用 表示
表示 关于
关于 的协变导数的分量,即
的协变导数的分量,即
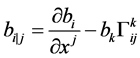 ,
,
并且记
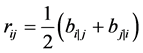 ,
, ,
, ,
,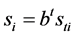 ,
,
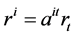 ,
, ,
, ,
, ,
, ,
,
其中 是度量矩阵
是度量矩阵 的逆矩阵,
的逆矩阵, 是
是 关于
关于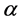 的对偶向量场的分量。同时,注意记号
的对偶向量场的分量。同时,注意记号 和
和 分别表示
分别表示 和
和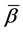 关于相应的黎曼度量
关于相应的黎曼度量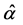 和
和 的协变导数。
的协变导数。
引理3.3:设 为
为 关于
关于 模长,则
模长,则
 。
。
证明:
 。
。
引理3.4:设 ,
,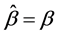 ,则
,则
 , (3)
, (3)
 。 (4)
。 (4)
证明:设
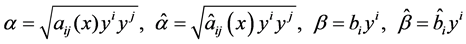 ,
,
由假设知,
 ,
,
所以
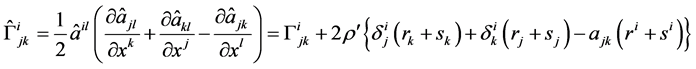 ,
,
 ,
,
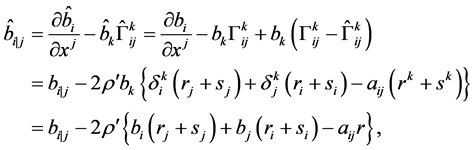
从而引理得证。
由(1)和(3)易知,为了使 是射影平坦的,即使得
是射影平坦的,即使得 的测地系数
的测地系数 具有
具有 的形式,只需使
的形式,只需使
 ,
,
由(2)易知
 ,
,
从而
 ,
,
于是,可取
 ,(5)
,(5)
此时,由(3)和(4)知
 。 (6)
。 (6)
引理3.5:设 ,
, ,则
,则
 。 (7)
。 (7)
证明:由假设知,
 ,
,
从而引理得证。
在(5)的基础上,由(6)和(7)易知
 ,
,
从而若取
 , (8)
, (8)
则
 ,
,
即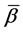 是关于
是关于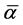 的闭的共形1形式。
的闭的共形1形式。
上述讨论表明,若 是局部射影平坦的,则通过对
是局部射影平坦的,则通过对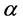 和
和 实施适当的形变,可以得到一个局部射影平坦的黎曼度量
实施适当的形变,可以得到一个局部射影平坦的黎曼度量 以及关于它的闭的共形1形式
以及关于它的闭的共形1形式 。显然,上述形变过程是可逆的,从而我们可以从
。显然,上述形变过程是可逆的,从而我们可以从 和
和 出发,构造局部射影平坦的芬斯勒度量
出发,构造局部射影平坦的芬斯勒度量 。由此,我们便得到如下定理:
。由此,我们便得到如下定理:
定理3.6:芬斯勒度量 是局部射影平坦的,当且仅当
是局部射影平坦的,当且仅当
 ,
,
其中是 局部射影平坦的黎曼度量,
局部射影平坦的黎曼度量, 是关于
是关于 的闭的共形1形式,
的闭的共形1形式,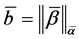 。此时,
。此时,
 。
。
证明:结合前面的讨论,我们只需再计算 与
与 的关系。事实上,
的关系。事实上,
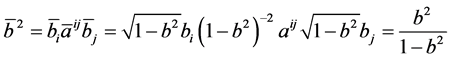 ,
,
从而
 ,
,
从而由(5)和(8)知
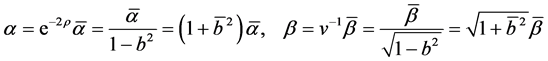 ,
,
定理得证。
基金项目
受国家自然科学基金资助,项目号11401225。
文章引用
余昌涛, (2015) 局部射影平坦Berwald型(α, β)度量的一个刻画
A Characterization for Locally Projectively Flat Berwald Type (α, β)-Metrics. 理论数学,04,150-155. doi: 10.12677/PM.2015.54023
参考文献 (References)
- 1. 沈一兵, 沈忠民 (2013) 现代芬斯勒几何初步. 高等教育出版社, 北京.
- 2. Bao, D., Chern, S.-S. and Shen, Z.M. (2000) An introduction to riemann-finsler geometry. Graduate Texts in Mathe- matics, Volume 200, Springer. http://dx.doi.org/10.1007/978-1-4612-1268-3
- 3. Cheng, X.Y. and Shen, Z.M. (2012) Finsler geometry—An approach via randers spaces. Science Press, Beijing.
- 4. Chern, S.-S. and Shen, Z.M. (2005) Riemann-finsler geometry. World Scientific, Singapore.
- 5. Berwald, L. (1929) Über die n-dimensionalen Geometrien konstanter Krümmung. in denen die Geraden die kürzesten sind. Mathematische Zeitschrift, 30, 449-469. http://dx.doi.org/10.1007/BF01187782
- 6. Mo, X.H., Shen, Z.M. and Yang, C.H. (2006) Some constructions of projectively flat finsler metrics. Science in China (Series A), 49, 703-714. http://dx.doi.org/10.1007/s11425-006-0703-7
- 7. Li, B.L. and Shen, Z.M. (2007) On a class of projectively flat finsler metrics with constant flag curvature. International Journal of Mathematics, 18, 749. http://dx.doi.org/10.1142/S0129167X07004291
- 8. Zhou, L.F. (2010) A local classfication of a class of (α,β) metrics with constant flag curvature. Differential Geometry and its Applications, 28, 170-193. http://dx.doi.org/10.1016/j.difgeo.2009.05.008
- 9. Shen, Z.M. and Yu, C.T. (2014) On einstein square metrics. Publicationes Mathematicae-Debrecen, 85, 413-424. http://dx.doi.org/10.5486/PMD.2014.6015
- 10. Chen, B., Shen, Z.M. and Zhao, L.L. (2013) On a class of ricci-flat finsler metrics in finsler geometry. Journal of Geometry and Physics, 70, 30-38. http://dx.doi.org/10.1016/j.geomphys.2013.03.009
- 11. Sevim, E.S., Shen, Z.M. and Zhao, L.L. (2012) On a class of ricci-flat douglas metrics. International Journal of Mathematics, 23, 1250046. http://dx.doi.org/10.1142/S0129167X12500462
- 12. Shen, Z.M. and Yildirim, G.C. (2008) On a class of projectively flat metrics with constant flag curvature. Canadian Journal of Mathematics, 60, 443-456. http://dx.doi.org/10.4153/CJM-2008-021-1