Pure Mathematics
Vol.05 No.05(2015), Article ID:16060,5
pages
10.12677/PM.2015.55029
Convergence on Preconditioned Block AOR Iterative Method of H-Matrix
Chunyun Zhao
Zhangye Middle School, Zhangye Gansu
Email: zyzxzcy@126.com
Received: Aug. 30th, 2015; accepted: Sep. 18th, 2015; published: Sep. 21st, 2015
Copyright © 2015 by author and Hans Publishers Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/



ABSTRACT
We consider block AOR preconditioned iterative method for solving the linear system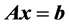 , using the preconditioning technology. When the coefficient matrix A is an H-matrix, the convergence results of the presented method are given.
, using the preconditioning technology. When the coefficient matrix A is an H-matrix, the convergence results of the presented method are given.
Keywords:H-Matrix, Block AOR Iterative Method, The Preconditioned Matrix, The Convergence

一种H-矩阵的块预条件AOR迭代法的收敛性
赵春云
张掖中学,甘肃 张掖
Email: zyzxzcy@126.com
收稿日期:2015年8月30日;录用日期:2015年9月18日;发布日期:2015年9月21日

摘 要
本文利用块预条件技术考虑了解线性方程组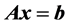 的块预条件AOR迭代法。当方程组的系数矩阵
的块预条件AOR迭代法。当方程组的系数矩阵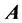 是H-矩阵时,得出了该方法的收敛性结果。
是H-矩阵时,得出了该方法的收敛性结果。
关键词 :H-矩阵,块AOR迭代法,预条件矩阵,收敛性

1. 引言
考虑线性方程组:
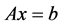 (1)
(1)
其中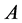 是
是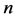 阶方阵,
阶方阵,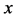 与
与 是
是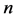 维向量。对(1)基本的迭代解法是:
维向量。对(1)基本的迭代解法是:
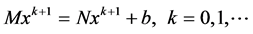 (2)
(2)
其中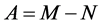 且
且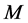 是非奇异矩阵,这样(2)也可被写成:
是非奇异矩阵,这样(2)也可被写成:
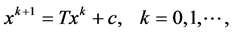
其中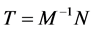 ,
,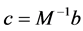 。
。
对矩阵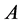 做如下分块:
做如下分块:
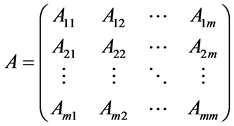 (3)
(3)
这儿,每个对角块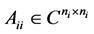 ,
,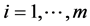 ,非奇,并且
,非奇,并且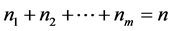 。如果
。如果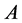 是非奇的,我们称
是非奇的,我们称 是非奇块矩阵。
是非奇块矩阵。
通常,把矩阵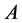 分裂成:
分裂成:
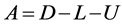
其中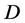 ,
,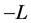 和
和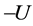 分别是(3)中
分别是(3)中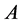 的块对角,严格块下三角和严格块上三角部分,这样,矩阵
的块对角,严格块下三角和严格块上三角部分,这样,矩阵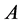 的块AOR迭代矩阵为:
的块AOR迭代矩阵为:

其中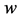 和
和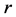 是两个实参数,并且
是两个实参数,并且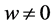 。特别地,当
。特别地,当 和
和 取一些特殊值时,我们得到块SOR,块Gauss-Seidel和块Jacobi迭代法。
取一些特殊值时,我们得到块SOR,块Gauss-Seidel和块Jacobi迭代法。
为了更好的解(1),引入了非奇块预条件矩阵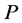 ,即考虑:
,即考虑:
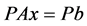 (4)
(4)
那么(4)的块AOR迭代格式为:
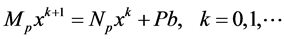 (5)
(5)
其中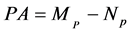 ,
,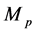 是非奇异矩阵。这样(5)也可以表示为:
是非奇异矩阵。这样(5)也可以表示为:
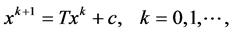
这儿,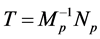 ,
, 。相似地,我们有块预条件SOR迭代法,块预条件Gauss-Seidel迭代法和块预条件Jacobi迭代法。
。相似地,我们有块预条件SOR迭代法,块预条件Gauss-Seidel迭代法和块预条件Jacobi迭代法。
如果 是一个
是一个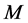 -矩阵,Alanelli等在[1] 中取
-矩阵,Alanelli等在[1] 中取 ,其中
,其中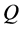 是由
是由 所构成的块对角矩阵(
所构成的块对角矩阵(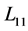 是
是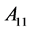 做
做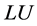 三角分解的下三角矩阵):
三角分解的下三角矩阵):
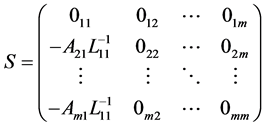
从文献[1] 可以看出若块预条件矩阵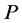 选择得合适,必将会提高迭代方法的收敛速度。本文在已经有的预条件矩阵的基础上引入参数,对(1)中系数矩阵
选择得合适,必将会提高迭代方法的收敛速度。本文在已经有的预条件矩阵的基础上引入参数,对(1)中系数矩阵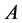 是
是 -矩阵的情形进行了考虑,引入了新的块预条件矩阵,理论上分析了块预条件迭代法的收敛性。
-矩阵的情形进行了考虑,引入了新的块预条件矩阵,理论上分析了块预条件迭代法的收敛性。
2. 预条件迭代法
我们考虑预条件矩阵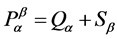 ,其中
,其中
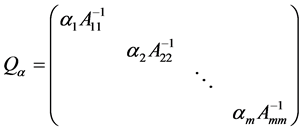 ,
,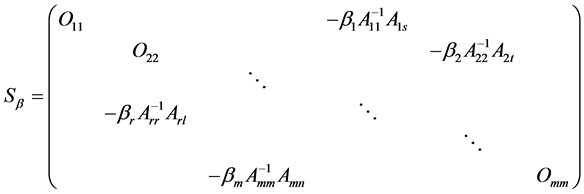
令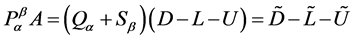 ,则
,则
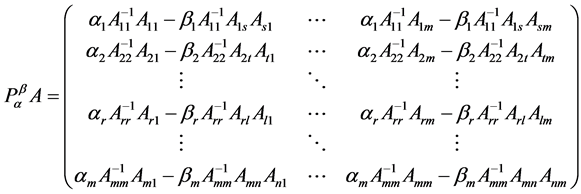
其中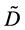 是由
是由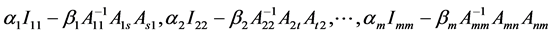 所构成的块对角矩阵,
所构成的块对角矩阵,
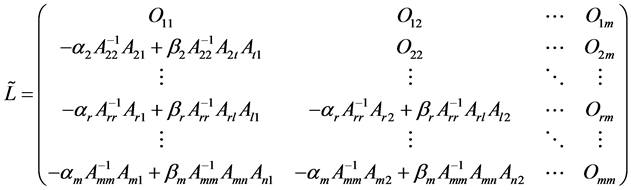
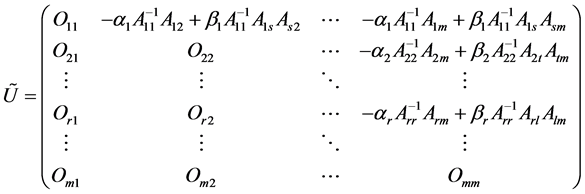
如果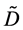 非奇,那么
非奇,那么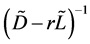 是存在的,这样,我们就可以定义
是存在的,这样,我们就可以定义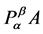 的块预条件AOR迭代法。即:
的块预条件AOR迭代法。即:
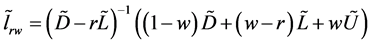
让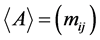 表示矩阵
表示矩阵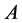 的比较矩阵,这儿
的比较矩阵,这儿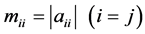 ,
,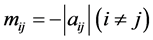 。
。
在上面的定义下,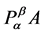 的比较矩阵为
的比较矩阵为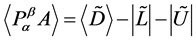 ,即:
,即:
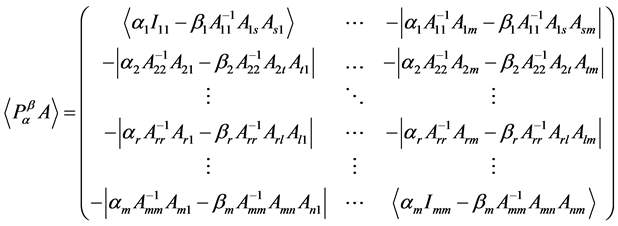
3. 预备知识
定义1 [2] :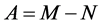 ,
, 非奇,被称为矩阵
非奇,被称为矩阵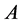 的一个分裂。如果
的一个分裂。如果 ,
,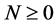 ,那么
,那么 被称为正则分裂。如果
被称为正则分裂。如果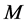 是非奇
是非奇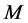 -矩阵,
-矩阵,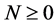 ,那么
,那么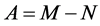 被称为
被称为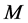 -分裂。
-分裂。
引理1 [2] :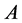 是
是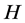 -矩阵的充要条件是存在
-矩阵的充要条件是存在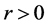 使
使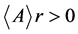 ,其中
,其中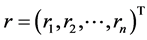 。
。
引理2 [3] [4] :如果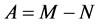 是
是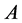 的一个
的一个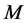 -分裂,那么
-分裂,那么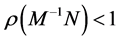 的充要条件是
的充要条件是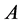 是一个非奇
是一个非奇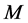 -矩阵。
-矩阵。
引理3 [5] :设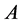 和
和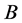 是两个
是两个 阶方阵且
阶方阵且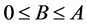 ,那么
,那么 。
。
引理4 [3] [6] :如果 是
是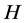 -矩阵,那么
-矩阵,那么 。
。
引理5 [7] :如果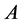 和
和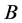 是两个
是两个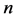 阶矩阵,那么
阶矩阵,那么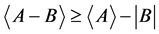 。
。
4. 主要结论及证明
定理1:让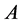 是一个非奇
是一个非奇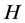 -矩阵,若有
-矩阵,若有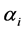 ,
,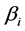 都大于0且:
都大于0且:
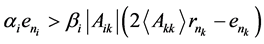
那么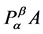 也是一个非奇
也是一个非奇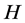 -矩阵。其中
-矩阵。其中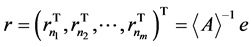 且
且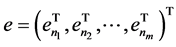 和
和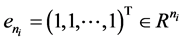 ,
,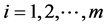 ,且与矩阵
,且与矩阵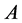 有相同的分块形式。
有相同的分块形式。
证明:由于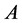 是一个非奇
是一个非奇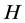 -矩阵,那么
-矩阵,那么 。
。
令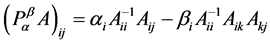 ,
,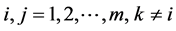 那么:
那么:
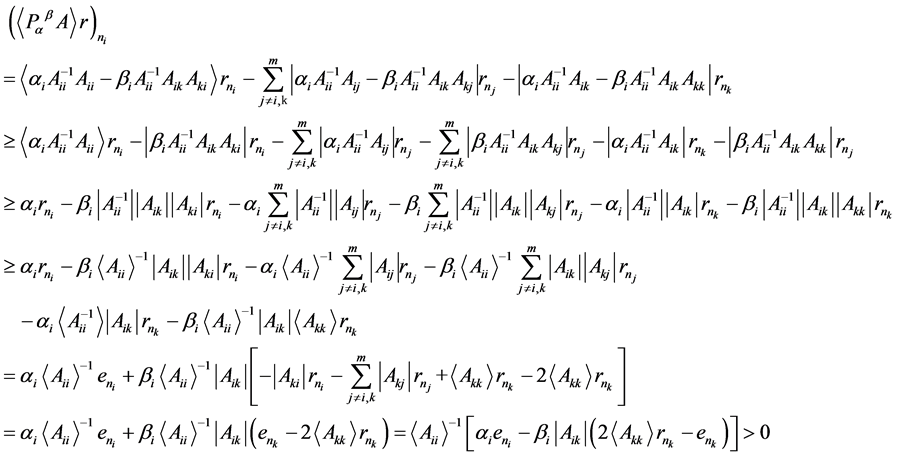
因此, 是一个非奇
是一个非奇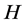 -矩阵,所以
-矩阵,所以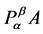 是一个非奇
是一个非奇 -矩阵。
-矩阵。
定理2:如果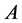 是一个非奇
是一个非奇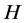 -矩阵,
-矩阵,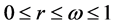 ,
,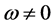 ,并且
,并且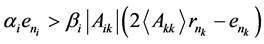 。
。
那么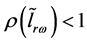 。
。
证明:由定理1知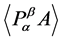 是一个非奇
是一个非奇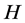 -矩阵,且
-矩阵,且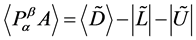 。
。
那么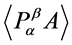 的AOR迭代矩阵为:
的AOR迭代矩阵为:
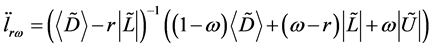
由引理2知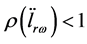 。因为:
。因为:
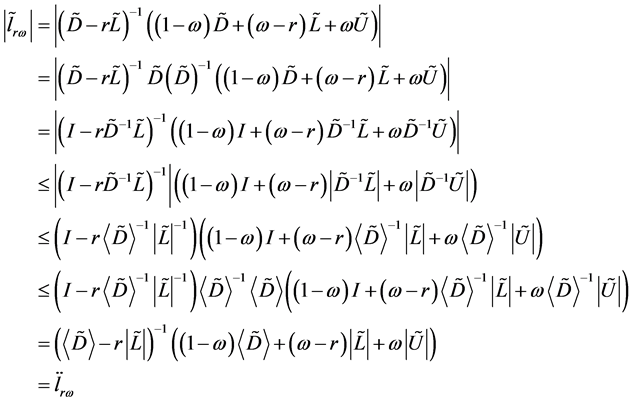
所以,由引理3,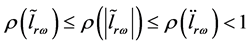 。
。
文章引用
赵春云. 一种H-矩阵的块预条件AOR迭代法的收敛性
Convergence on Preconditioned Block AOR Iterative Method of H-Matrix[J]. 理论数学, 2015, 05(05): 207-211. http://dx.doi.org/10.12677/PM.2015.55029
参考文献 (References)
- 1. Anelli, M. and Hadjidimos, A. (2004) Block Gauss elimination followed by a classical. Iterative method for the solution of linear systems. Computational and Applied Mathematics, 163, 381-400. http://dx.doi.org/10.1016/j.cam.2003.08.045
- 2. 王学忠, 李晓梅 (2012) H-矩阵的预条件对角占优性. 理论数学, 1, 39-44.
- 3. Li, W. and You, Z.Y. (1998) The multi-parameters overrelaxation method. Journal of Computational Mathematics, 16, 231-238.
- 4. Varga, R.S. (1981) Matrix iterative analysis. Prentice-Hall, Englewood Cliffs.
- 5. Berman, A. and Plemmons, R.J. (1994) Nonnegative matrices in the mathematical sciences. SIAM, Philadelphia. http://dx.doi.org/10.1137/1.9781611971262
- 6. Kolotilina, L.Yu. (1995) Two-sided bounds for the inverse of an H-matrix. Linear Algebra and Its Applications, 225, 117-123. http://dx.doi.org/10.1016/0024-3795(93)00325-T
- 7. 黄延祝, 杨传胜 (2007) 特殊矩阵分析及应用. 科学出版社, 北京.