Pure Mathematics
Vol.05 No.06(2015), Article ID:16436,6
pages
10.12677/PM.2015.56040
Approximate Inertial Manifold of Strongly Damped Wave Equation
Sufang Zhang, Jianwen Zhang
College of Mathematics, Taiyuan University of Technology, Taiyuan Shanxi
Received: Nov. 4th, 2015; accepted: Nov. 21st, 2015; published: Nov. 27th, 2015
Copyright © 2015 by authors and Hans Publishers Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/



ABSTRACT
In this paper, the global attractor approximation by smooth manifold is considered in strongly damped equation. A nonlinear approximate inertial manifold of strongly damped wave equation is constructed. The order of approximation of the inertial manifold to the global attractor is obtained.
Keywords:Strongly Damped, Approximate Inertial Manifold, Wave Equation

强阻尼波动方程的近似惯性流形
张素方,张建文
太原理工大学数学学院,山西 太原

收稿日期:2015年11月4日;录用日期:2015年11月21日;发布日期:2015年11月27日

摘 要
本文主要研究了强阻尼波动方程的整体吸引子由光滑流形来逼近。构造了强阻尼波动方程的一个非线性近似惯性流形,并得到了该近似惯性流形逼近整体吸引子的阶数估计。
关键词 :强阻尼,近似惯性流形,波动方程

1. 引言
本文研究了下列一类带强阻尼项 的高维波动方程:
的高维波动方程:
 (1)
(1)
其中 为有界光滑闭区域,
为有界光滑闭区域, 为常数,函数
为常数,函数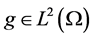 。
。
该波动方程来自非线性弹性杆在纵向形变波传播与弱非线性作用下空间变换离子波传播问题见[1] [2] ,这是一个具有耗散性质的无穷维动力系统,而耗散动力系统的基本特征由相应的整体吸引子所表现见[3] [4] 。由于整体吸引子结构复杂,甚至有些物理系统的整体吸引子的分形维数是无限维的。考虑到在实际中的应用,如数值模拟,G. Foias等在见[5] 首次引进了惯性流形的概念,具体思想是把整体吸引子嵌入到一个适当的光滑的有限维流形,原系统在这个有限维流形上约化以后的动力学行为能通过一个常微分方程来实现。但是保证惯性流形存在的条件十分苛刻,于是想到了用一种近似的、光滑的、比较容易求解的流形去逼近整体吸引子和惯性流形,这就是近似惯性流形,近似惯性流形是有限维的光滑流形,且系统的每一个解在有限的时间里进入它的狭小的邻域内见[6] [7] 。
2. 预备知识
引进空间 ,
, ,
, ,则
,则 ,
,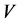 ,
, 均为Hilbert空间且空间
均为Hilbert空间且空间 ,
,
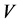 ,上的范数分别为:
,上的范数分别为: ,
, ,
,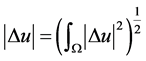 ,空间
,空间 ,
,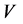 上的内积为:
上的内积为: ,
,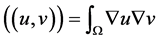 。
。
设 为
为 ,则
,则 为无界正自共轭算子,原方程(1)可化为如下的微分系统:
为无界正自共轭算子,原方程(1)可化为如下的微分系统:
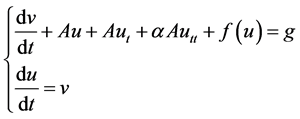 (2)
(2)
因为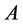 为无界正自共轭算子,
为无界正自共轭算子, 是紧的,
是紧的, 在
在 中稠,所以
中稠,所以 具有由算子
具有由算子 的特征向量所组成的正交基
的特征向量所组成的正交基 ,
, ,
, ,设
,设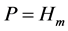 为
为 的投影。
的投影。 为
为 的投影。设
的投影。设 ,
, ,
, ,
, ,则把投
,则把投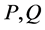 作用在方程(2)上有
作用在方程(2)上有
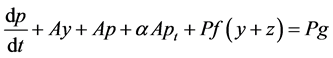 (3)
(3)
 (4)
(4)
 (5)
(5)
 (6)
(6)
函数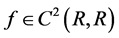 ,满足下面的条件:
,满足下面的条件:
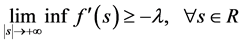 (7)
(7)
 (8)
(8)
 (9)
(9)
其中 为常数。
为常数。
定理1:设 ,如果
,如果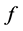 满足条件(7)-(9),
满足条件(7)-(9),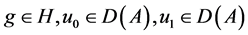 ,则方程(1)存在唯一解
,则方程(1)存在唯一解 ,且满足
,且满足

证明:略由Faedo-Galerkin方法,我们可以获得唯一解见[7] [8]
引理1:设 ,
,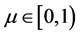 ,如果函数
,如果函数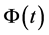 是定义在
是定义在 上绝对连续的正函数,即对任意的
上绝对连续的正函数,即对任意的 ,
, ,
, ,且满足不等式
,且满足不等式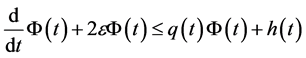 ,则存在
,则存在 ,当
,当 时,
时,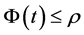 ,
,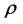 是常数,见[7] 。
是常数,见[7] 。
3. 主要结果及其证明
设 为banbch空间,空间
为banbch空间,空间 模分别记为
模分别记为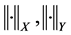 ,对任意
,对任意 ,空间
,空间 上的模记为
上的模记为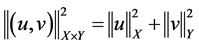 。
。
定理2:设 ,如果
,如果 满足条件(7)~(9),
满足条件(7)~(9), ,则存在
,则存在 ,当
,当 时,
时, 。
。
证明:设 ,在
,在 中让(1)与
中让(1)与 作内积,可得
作内积,可得

设 且
且 ,
,
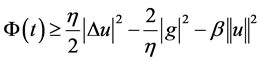 (10)
(10)
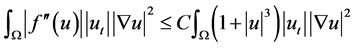 (11)
(11)
 (12)
(12)
 (13)
(13)
由(10)~(13)式,可得
 (14)
(14)
 (15)
(15)
 (16)
(16)
设 ,
, ,此时(14)式可以重写为
,此时(14)式可以重写为
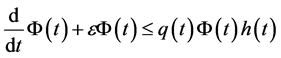 (17)
(17)
定理证毕。
现考虑问题(2)的近似惯性流形,设 为
为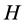 在
在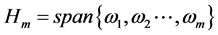 上的正交投影。
上的正交投影。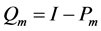 。令
。令 ,则(2)等价于
,则(2)等价于
 (18)
(18)
 (19)
(19)
为用光滑流形逼近整体吸引子,先设
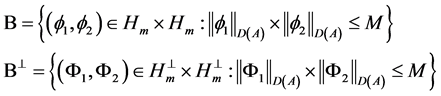
定义映射 即
即 ,且满足
,且满足
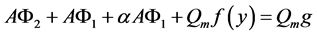 (20)
(20)
 (21)
(21)
则 是原方程的近似惯性流形。
是原方程的近似惯性流形。
首先证明映射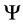 的存在性。
的存在性。
定理3设 充分大,使得
充分大,使得 且
且 ,则映射
,则映射 存在,且有
存在,且有 。
。
证明:定义映射 ,任意
,任意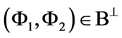 ,有
,有 ,
,
满足
 (22)
(22)
 (23)
(23)
为证明映射 的存在性,只需证明映射
的存在性,只需证明映射 存在不动点,因此只需证明
存在不动点,因此只需证明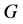 为压缩映射。
为压缩映射。
下证 。由于
。由于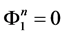 ,所以
,所以 。再由(22),有
。再由(22),有

由定理1知 有界,由条件(7)~(9)知
有界,由条件(7)~(9)知 有界,所以有
有界,所以有 ,即
,即
 (24)
(24)
所以有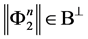 。
。
下证 为压缩映射。由于
为压缩映射。由于 是常值映射,所以存在.
是常值映射,所以存在.
其次设 ,由
,由 ,及(24),有
,及(24),有
 (25)
(25)
 (26)
(26)
上述两式相减得,
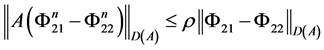 (27)
(27)
所以
 (28)
(28)
只要 足够大,就可使得
足够大,就可使得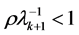 ,即
,即 为压缩映射,所以
为压缩映射,所以 是存在的,
是存在的,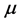 为系统的近似惯性流行。
为系统的近似惯性流行。
定理4:设 充分大,使得
充分大,使得 且
且 ,则存在正常数
,则存在正常数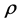 ,有
,有

证明:用(21)减去(19),得

由定理1,紧嵌入定理及poincare不等式有 ,所以
,所以
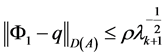 (29)
(29)
用(5)减去(19),得
 (30)
(30)
所以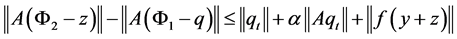 。
。
由定理1知 有界,由条件(7)~(9)知
有界,由条件(7)~(9)知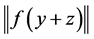 有界,所以
有界,所以 有界,故
有界,故
 (31)
(31)
由(29)(31),定理得证。
基金项目
国家自然科学基金(11172194)、山西省软科学(2014041007-3)。
文章引用
张素方,张建文. 强阻尼波动方程的近似惯性流形
Approximate Inertial Manifold of Strongly Damped Wave Equation[J]. 理论数学, 2015, 05(06): 278-283. http://dx.doi.org/10.12677/PM.2015.56040
参考文献 (References)
- 1. Clarkson, P.A., Leveque, R.J. and Saxton, R.A. (1986) Solitary-Wave Interaction in Elastic Rods. Studies in Applied Mathematics, 75, 95-122. http://dx.doi.org/10.1002/sapm198675295
- 2. Seyler, C.E. and Fanstermacher, D.L. (1984) Asymmetric Regularized Long Wave Equation. Physics of Fluids, 27, 58-66.
- 3. Xie, Y.Q. and Zhong, C.K. (2009) Asymptotic Behavior of a Class Nonlinear Evolution Equation. Nonlinear Analysis, 71, 5095-5105. http://dx.doi.org/10.1016/j.na.2009.03.086
- 4. Xie, Y.Q., Yang, L. and Qin, G.X. (2007) Strain Solitary Waves in a Nonlinear Elastic Rod. Journal of Hunan University, 34, 58-61.
- 5. Foias, C., Sell, G. and Temam, R. (1985) Varies Inertilles des Equations Differentials Dissipative. C. R. Acad Sci. Paris Ser I Math, I301, 139-142.
- 6. 蒲志林, 陈光淦. 非线性Schodinger-Boussnesq的近似惯性流形[J]. 四川师范大学学报: 自然科学版, 2005, 28(4): 419-421.
- 7. 魏赟赟, 陈光淦. 非自治反应扩散方程的近似惯性流形[J]. 四川师范大学学报: 自然科学版, 2005, 28(4): 419-421.
- 8. Xie, Y.Q. and Zhong, C.K. (2007) The Existence of Global Attractors for a Class Nonlinear Evolution Equation. Journal of Mathematical Analysis and Applications, 336, 54-69. http://dx.doi.org/10.1016/j.jmaa.2006.03.086