Pure Mathematics
Vol.06 No.02(2016), Article ID:17249,5
pages
10.12677/PM.2016.62017
Entire Solutions of Fermat Type Functional Equations
Jiangmei Duan, Min Su
Department of Mathematics, Yunnan Normal University, Yunnan Kunming

Received: Mar. 10th, 2016; accepted: Mar. 23rd, 2016; published: Mar. 30th, 2016
Copyright © 2016 by authors and Hans Publishers Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/



ABSTRACT
In this paper, a new proof is given for the result that if , there are no non-constant entire solutions of the functional equation
, there are no non-constant entire solutions of the functional equation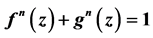 .
.
Keywords:Fermat Type Functional Equation, Entire Functions, Normal Families Theory

关于Fermat型函数方程的整函数解
段江梅,苏敏
云南师范大学数学学院,云南 昆明

收稿日期:2016年3月10日;录用日期:2016年3月23日;发布日期:2016年3月30日

摘 要
本文对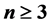 时,函数方程
时,函数方程 没有非常数整函数解的结果给出新的证明。
没有非常数整函数解的结果给出新的证明。
关键词 :Fermat型函数方程,整函数,正规族理论

1. 引言及主要结果
1637年法国数学家费马提出了如下猜想:当 时,丢番图方程
时,丢番图方程 没有非平凡的整数解。1994年这个猜想被英国数学A. Wiles完全证明。要寻找方程
没有非平凡的整数解。1994年这个猜想被英国数学A. Wiles完全证明。要寻找方程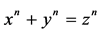 在整数环上的非平凡解,可以转化为求代数曲线
在整数环上的非平凡解,可以转化为求代数曲线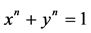 上的有理点。
上的有理点。
然而早在1965年,当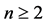 时,关于Fermat型函数方程
时,关于Fermat型函数方程
 (1)
(1)
在整函数环,或是亚纯函数域上的非平凡解的状况已经完全清楚了。容易证明:当 时,函数方程(1)不存在非常数的整函数解;当
时,函数方程(1)不存在非常数的整函数解;当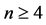 时,函数方程(1)不存在非常数亚纯函数解。
时,函数方程(1)不存在非常数亚纯函数解。
类似地,研究丢番图方程 整数解的存在性问题可以转化为研究方程
整数解的存在性问题可以转化为研究方程 的有理数解的存在性问题。然而,当
的有理数解的存在性问题。然而,当 时,方程
时,方程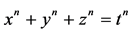 整数解的状况不是十分清楚。
整数解的状况不是十分清楚。
相应地,不妨先考虑当 时,Fermat型函数方程
时,Fermat型函数方程
 (2)
(2)
在整函数环,或是亚纯函数域上的非平凡解。对于该问题的研究已有如下结论:
1985年W. K. Hayman [1] 证明了:当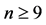 时,方程(2)不存在非常数亚纯解;当
时,方程(2)不存在非常数亚纯解;当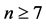 时,方程(2)不存在非常数整函数解。此外,当
时,方程(2)不存在非常数整函数解。此外,当 时,G. G. Gundersen [2] - [4] 等人找到了满足方程(2)的非常数整函数解;当
时,G. G. Gundersen [2] - [4] 等人找到了满足方程(2)的非常数整函数解;当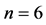 时,G. G. Gundersen [5] 构造了满足方程(2)的非常数亚纯解。
时,G. G. Gundersen [5] 构造了满足方程(2)的非常数亚纯解。
近期,苏敏 [6] 等人证明了:当 时,方程(2)不存在级小于1的非常数整函数解;当
时,方程(2)不存在级小于1的非常数整函数解;当 时,方程(2)不存在级小于1的非常数亚纯函数解。
时,方程(2)不存在级小于1的非常数亚纯函数解。
本文主要利用正规族理论的知识对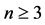 时,函数方程(1)没有非常数整函数解的结果给出新的证明。
时,函数方程(1)没有非常数整函数解的结果给出新的证明。
对于探究函数方程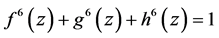 整函数解的存在性,运用本文的方法,利用正规族理论的Zalcman引理对特殊情况的整函数解作降级处理,具有一定的可行性。
整函数解的存在性,运用本文的方法,利用正规族理论的Zalcman引理对特殊情况的整函数解作降级处理,具有一定的可行性。
定理1:当 时,函数方程(1)没有级小于等于1的非常数整函数解。
时,函数方程(1)没有级小于等于1的非常数整函数解。
定理2:当 时,函数方程(1)没有非常数整函数解。
时,函数方程(1)没有非常数整函数解。
2. 几个概念与引理
在定理1的证明之前,先介绍本文中常用的几个概念与引理:
定义1 [7] :设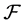 为区域
为区域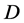 内的一族亚纯函数,如果从该族中的每一个函数序列
内的一族亚纯函数,如果从该族中的每一个函数序列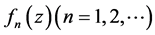 可以选出一个子序列
可以选出一个子序列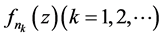 满足下列两个条件之一:
满足下列两个条件之一:
1) 在
在 内闭一致收敛;
内闭一致收敛;
2)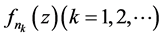 在
在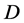 内闭一致趋于
内闭一致趋于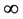 ,
,
则称此函数族 在
在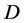 内是正规的。
内是正规的。
定义2 [7] :设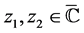 ,我们称一非负实数为
,我们称一非负实数为 与
与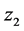 之间的球面距离,记作
之间的球面距离,记作 :
:

定义3 [7] :设 在
在 内亚纯,我们称
内亚纯,我们称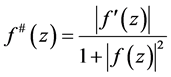 为
为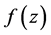 的球面导数。
的球面导数。
定义4 [7] :设 为
为 上的亚纯函数,
上的亚纯函数,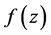 的级定义为
的级定义为 。
。
引理1 [8] :设 为
为 上的非常数亚纯函数,其级
上的非常数亚纯函数,其级 有穷,则对于
有穷,则对于 ,存在
,存在 ,使得
,使得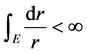 ,且
,且
 .
.
引理2 [7] :(Marty定则)设 为区域
为区域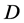 内的一族亚纯函数。
内的一族亚纯函数。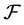 在
在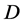 内正规的充要条件是:对于
内正规的充要条件是:对于 内的任一有界闭区域
内的任一有界闭区域 ,存在相应的正数
,存在相应的正数 (与
(与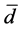 有关),使得对于
有关),使得对于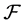 中的每一个函数
中的每一个函数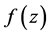 ,有
,有

即 。
。
引理3 [7] :设 为区域
为区域 内的一族亚纯函数。如果
内的一族亚纯函数。如果 在
在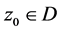 内不正规,则存在
内不正规,则存在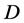 中的点列
中的点列 ,
,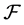 中的函数列
中的函数列 ,正数列
,正数列 及
及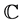 上的非常数亚纯函数
上的非常数亚纯函数 ,使得当
,使得当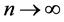 时,
时, 且
且
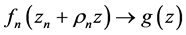 (按球面距离在上内闭一致收敛),
(按球面距离在上内闭一致收敛),
并且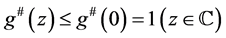 。特别地,
。特别地, 的级不超过2。
的级不超过2。
引理4 [7] :设 为整函数。若
为整函数。若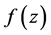 的球面导数
的球面导数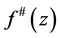 有界,则
有界,则 的级至多为1。
的级至多为1。
引理5 [7] :若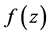 是无穷级亚纯函数,则存在一个序列
是无穷级亚纯函数,则存在一个序列 ,使得当
,使得当 时,有
时,有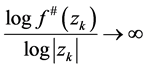 。
。
3. 定理的证明
3.1. 定理1的证明
假设函数方程(1)存在级小于等于1的非常数整函数解 ,则
,则 一定线性无关,故
一定线性无关,故 。
。
由(1)式可得方程组

令 ,则
,则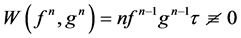 ,显然
,显然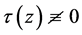 。
。
另一方面,由克莱姆法则得
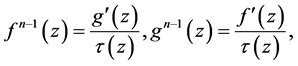
从而
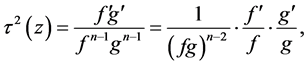 (3)
(3)
故 。
。
由题设和(1)式知: ,
,
故由引理1知:对任意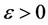 ,存在
,存在 ,使
,使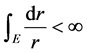 ,且
,且
 ,
,
从而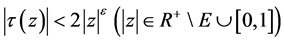 ,
,
又由于 为整函数,所以
为整函数,所以 为常数,设
为常数,设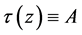 。下面证明:
。下面证明: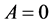 。
。
我们断言: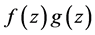 为非常数整函数。事实上,若
为非常数整函数。事实上,若 ,则
,则
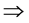
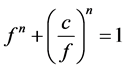 ,所以
,所以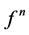 不取0,1,这与
不取0,1,这与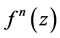 至多有一个有穷picard例外值矛盾。
至多有一个有穷picard例外值矛盾。
由于 为非常数整函数,故存在
为非常数整函数,故存在 ,使当
,使当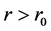 时,
时,
 (4)
(4)
又由(3)、(4)式及引理1知:对上述的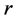 及
及 ,存在
,存在 ,使
,使 ,且
,且
 ,
,
由于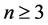 ,令
,令 ,
,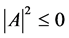 ,故
,故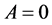 即
即 ,矛盾,定理1得证。
,矛盾,定理1得证。
3.2. 定理2的证明
假设函数方程(1)存在非常数的整函数解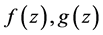 ,那么由
,那么由 的任意性可以得到一组无穷级的整函数解
的任意性可以得到一组无穷级的整函数解 。
。
由于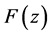 是无穷级整函数,由引理5知存在一个序列
是无穷级整函数,由引理5知存在一个序列 ,使得当
,使得当 时,有
时,有
 (5)
(5)
记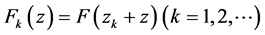 ,
,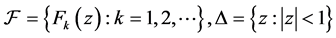 ,由于
,由于

结合(5)式知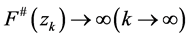 ,所以
,所以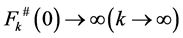 。于是由引理2知:
。于是由引理2知: 在原点的某邻域内不正规,从而由引理3知:存在点列
在原点的某邻域内不正规,从而由引理3知:存在点列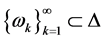 ,正数列
,正数列 ,
, 中的函数列不妨仍记为
中的函数列不妨仍记为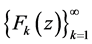 以及
以及 中的非常数整函数
中的非常数整函数 ,使得当
,使得当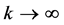 时,
时, ,且
,且
 (按球面距离在上内闭一致收敛),
(按球面距离在上内闭一致收敛),
即
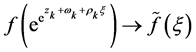 (按球面距离在上内闭一致收敛),
(按球面距离在上内闭一致收敛),
并且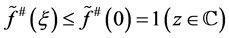 ,再由引理4知,
,再由引理4知,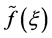 的级
的级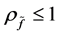 ,
,
此时必存在函数列 ,
,
使得当 时,
时,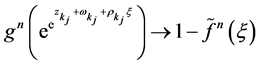 (按球面距离在
(按球面距离在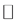 上内闭一致收敛),
上内闭一致收敛),
故存在非常数的整函数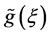 使得
使得 ,
,
即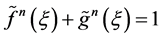 ,故
,故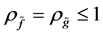 ,与定理1矛盾,定理2得证。
,与定理1矛盾,定理2得证。
文章引用
段江梅,苏 敏. 关于Fermat型函数方程的整函数解
Entire Solutions of Fermat Type Functional Equations[J]. 理论数学, 2016, 06(02): 116-120. http://dx.doi.org/10.12677/PM.2016.62017
参考文献 (References)
- 1. Hayman, W.K. (1985) Waring’s Problem für analytische Funktionen. Bayerische Akademie der Wissenschaften Ma-thematisch-Naturwissenschaftliche Klasse. Sitzungsberichte, 1984, 1-13.
- 2. Molluzzo, J. (1972) Monotonicity of Quadrature Formulas and Polynomial Representation. Doctoral Thesis, Yeshiva University, New York.
- 3. Green, M. (1975) Some Picard Theorems for Holomorphic Maps to Algebraic Varieties. American Journal of Mathematics, 97, 43-75. http://dx.doi.org/10.2307/2373660
- 4. Gundersen, G.G. and Kauya Tohge. (2004) Entire and Meromor-phic Solutions of . Symposium on Complex Differential and Functional Equations, Report Series No. 6, Department of Mathematics, University of Joensuu, Joensuu, 57-67.
- 5. Gundersen, G.G. (1998) Me-romorphic Solutions of . Analysis, 18, 285-290.
- 6. 苏敏, 李玉华. 关于函数方程非平凡亚纯解的研究[J]. 云南师范大学学报: 自然科学版, 2009, 29(2): 41-44.
- 7. 顾永兴, 庞学诚, 方明亮. 正规族理论及其应用[M]. 北京: 科学出版社, 2007.
- 8. Chiang, Y.M. and Feng, S.J. (2008) On the Nevanlinna Characteristic of and Difference Equations in the Complex Plane. The Ramanujan Journal, 16, 105-129. http://dx.doi.org/10.1007/s11139-007-9101-1
- 9. 杨乐. 值分布理论及其新研究[M]. 北京: 科学出版社, 1982.