云南师范大学数学学院,云南 昆明
收稿日期:2023年6月5日;录用日期:2023年7月7日;发布日期:2023年7月14日

摘要
半群分解是一类经典的半群理论研究课题。本文主要围绕正则*–半群的可分解性进行研究。首先介绍正则*–半群及可分解的正则*–半群的相关概念,再用正则*–半带和群的半直积给出了可分解的正则*–半群和E-酉可分解的正则*–半群的刻画,推广了逆半群的相关结果。
关键词
正则*–半群,可分解,半直积

On Factorizable Regular*-Semigroups
Yuxin Wang
School of Mathematics, Yunnan Normal University, Kunming Yunnan
Received: Jun. 5th, 2023; accepted: Jul. 7th, 2023; published: Jul. 14th, 2023

ABSTRACT
Factorization of semigroups is a classic topic in semigroup theory. Factorizable regular*-semigroups are studied in this paper. The related concepts of regular*-semigroups and factorizable regular*-semigroups are introduced, and some characterizations of factorizable regular*-semigroups and E-unitary factorizable regular*-semigroups are obtained by the semidirect products of regular*-semibands and groups. This generalizes the corresponding results of inverse semigroups.
Keywords:Regular*-Semigroup, Factorizable, Semidirect Product

Copyright © 2023 by author(s) and Hans Publishers Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY 4.0).
http://creativecommons.org/licenses/by/4.0/


1. 引言
众所周知,群的分解是研究群的结构的重要方式。与此相仿,半群的分解理论在半群研究中也占有重要地位。上世纪60年代末,Tolo在 [1] 中介绍了半群分解的一些基本事实。逆半群是半群理论中研究成果最丰富的一类半群(见 [2] )。上世纪70年代,Chen和Hsieh在 [3] 中研究了可分解的逆半群。随后文献 [4] [5] 分别研究了弱可分解逆半群和可分解的变换半群。关于可分解的逆半群的更详细的结果可参见综述文章 [6] 。作为逆半群的一种推广,纯正半群在上世纪70年代被引入,目前也取得了比较丰富的结果(见 [7] )。特别的,2007年,文献 [8] 研究了纯正半群的可分解性。1978年,Nordahl和Scheiblich在文献 [9] 中介绍了逆半群的另一种推广形式,即正则*–半群。随后,这类半群得到了众多学者的关注,至今仍不断有新的结果出现(见 [10] )。本文的目的是介绍并研究正则*–半群的可分解性。在给出正则*–半群的一些必要概念和结果后,提出了可分解正则*–半群的概念,然后用正则*–半带和群的半直积给出了可分解的正则*–半群的结构。
2. 预备知识
设
是半群。记S的幂等元集为
。对任意
,记
.
设
是映射。称
为正则*–半群,若下述公理成立:
,
,
.
记
,并称
中元素为S的投射元。
引理2.1 [9] 设
是正则*–半群。
(1)
,
。
(2) 对任意
,
,有
。
(3) 每个
-类和
-类均含唯一的投射元。
(4)
当且仅当
。
(5)
当且仅当
。
称半群S正则,若对任意
,有
。易见,正则*–半群是正则半群。正则半群S称为纯正半群,若
形成S的子半群(子带)。
引理2.2 [7] 设
是正则*–半群。则S纯正当且仅当对任意
,有
。
设
为正则*–半群。记
生成的子半群为
,即
.
由引理2.1(1),
。若
,则称S是正则*–半带。特别的,若
,则称S是正则*–带。容易看出,若
是纯正的正则*–半群,则
形成正则*–带。
命题2.3 设
是正则*–半群。则
是正则*–半带。特别地,若S含单位元1,则
是含单位元的正则*–半带。
证明. 任取
,其中
。则
,
故
对运算*封闭,从而
是S的正则*–子半群。对任意
,有
,从而
。于是
。这表明
。故
是正则*–半带。若S含单位元1,则
,于是
是含单位元的正则*–半带。
设S是正则*–半群,称S是E-酉的,如果对任意
及
,
蕴含
。
命题2.4 设S是E-酉的正则*–半群。则
是正则*–带。
证明. 设
,
。则
。由于S是E-酉的,故
。由引理2.2知S纯正,从而
是正则*–带。由引理2.1(1)及
的定义知
,
从而
。
3. 主要结果及其证明
本节设S为正则*–半群,U是群,设U在S上有作用
,
且满足以下条件:对任意
及
,
,
,
,
.
在集合
上定义
,
.
命题3.1
关于上述运算形成正则*–半群,称为S和U的半直积,记为
。若S有单位元1,则
是
的单位元。进一步的,有
,
,
.
特别的,若S是正则*–半带,则
。
证明. 设
。则
这表明
是半群。又因为
,
故
是正则*–半群。进一步的,有
,从而
,
.
故
是
的单位元。另一方面,由上述证明知
。这说明
.
对任意
,有
.
故
。据引理2.1知
。最后由
及
的定义立得
。
命题3.2 设
是正则*–半群S与群U的半直积。则
(1)
当且仅当
。
(2)
当且仅当
。
证明. 由引理2.1(4)及事实
和
知(1)成立。另一方面,由引理2.1(5)及
和
知(2)成立。
称正则*–半群S是可分解的,若存在S的子群G使得
,且G的单位元为S的投射元。
下面的例子指出,可分解的正则*–半群未必是逆半群。
例3.3 设
是指标集,
,其中
.
记
。在S上定义乘法如下:对任意
,
,
.
则S关于乘法作成矩形带。记
,其中e是单位元。在
上规定一元运算“*”如下:
.
易验证
是正则*–半群且
,
。又
的单位元e所在的
-类只有e本身,所以
的单位群为
。于是
。故
是可分解的正则*–半群,并且
不是逆半群。
下面给出可分解的正则*–半群的一些性质。
命题3.4 设S是可分解的正则*–半群且
。则
(1) 对任意
,g在G中的逆元为
。
(2)
。
(3) G的单位元是S的单位元,记为1。
(4)
,其中
是S的单位群,即S的单位元1所在的
-类
。
证明. (1) 设1是G的单位元,
是g在G中的逆元。则由假设条件知
且 。另一方面,有
。另一方面,有 。故由引理2.1(3)知
,
。于是
。
。故由引理2.1(3)知
,
。于是
。
(2) 设
。因为
,所以存在
和
,使得
。由命题2.3及(1),
。故
。
(3) 设G的单位元是1。因为
,所以对任意
,存在
,
使得
。因此
。由(2)知
。所以对任意
,存在
,
使得
。因此
。这表明1是S的单位元。
(4) 因为
是S的包含1的极大子群,所以
。任取
。则由
知,存在
和
使得
。故
,从而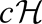 。由(1)和引理2.1(4)知
。记
,其中
。则由
知
。类似可证
。故
,从而
。这表明
。于是
。
。由(1)和引理2.1(4)知
。记
,其中
。则由
知
。类似可证
。故
,从而
。这表明
。于是
。
由命题3.4易得可分解的逆半群的下述已知结果。
命题3.5 [3] 设S是可分解的逆半群且
。则
(1)
。
(2) G的单位元是S的单位元,记为1。
(3)
,其中
是S的单位群,即S的单位元1所在的
-类
。
定理3.6 设S是正则*–半群。则下述几条等价:
(1) S可分解。
(2) S是某个含单位元的正则*–半带C和某个群U的半直积
的投射生成元分离的
-同态像。
(3) S是幺半群且是某个正则*–半带C和某个群U的半直积
的
-同态像。
证明. (1)
(2)。设S可分解。由命题3.4知S含单位元且
,其中
是S的单位群。据命题2.3,
是含单位元的正则*–半带。规定
在
上的作用如下:
,
,
,
,
则对任意
及
,由命题3.4(1),有
,  ,
,
,
.
由命题3.1可得
和
的半直积
。定义
,
.
下证
是投射生成元分离的满的
-同态。由命题3.1及命题2.3知
.
设
且
。则
,从而
。这表明
是投射生成元分离的。由于S可分解,故对任意
,存在
,
使得
。于是
且
。故
是满射。设
。则
,
.
因此
是
-同态。
若S是E-酉的,则由命题2.4知
。设
。则
。若
,则
,从而
。注意到
且S是E-酉的,有
。由于
,故
,从而
,
。这说明
是单射。故当S是E-酉可分解的正则*–半群时,
是同构映射。此时S同构于某个含单位元的正则*–带和某个群的半直积。
(2)
(3)。显然。
(3)
(1)。设S有单位元1,C是正则*–半带,U是群,
是C和U的半直积。又设
是
-满同态。则
。设
。则
.
于是
,
其中
。这表明,存在
使得
。
设
。则
据命题3.2,有
和
。于是
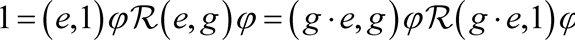 . (3.1)
. (3.1)
由
知
,从而
.
这导致
。据(3.1),
。由g的任意性得
。另一方面,由
及命题3.2得
,从而由(3.1)得 ,即
,即 ,于是
。
,于是
。
设
。因为S是
的
-同态像,故存在
,使得
,从而由
知
由命题3.1知
,从而
。据(3.1)式,有
.
故
。这就证明了S可分解。
推论3.7 设S是正则*–半群,则S是E-酉可分解的当且仅当S同构于某个含单位元的正则*–带和某个群的半直积。
证明. 由定理3.6证明中(1)
(2)部分的最后一段可得必要性。下证充分性。设B是一个含单位元的正则*–带,G是群,
是B和G的半直积。由命题2.3知S是幺半群。据定理3.6,S可分解。另一方面,据命题3.1知
。设
,
且
。
注意到
,
有
,从而
。故
是E-酉的。
将定理3.6及推论3.7用到逆半群的情况,有以下推论。
推论3.8 [2] 设S是逆半群。则下述几条等价:
(1) S可分解。
(2) S是某个含单位元的半格E和某个群G的半直积
的幂等元分离的
-同态像。
(3) S是幺半群且是某个半格E和某个群G的半直积
的
-同态像。
推论3.9 [2] 设S是逆半群,则S是E-酉可分解的当且仅当S同构于某个含单位元的半格和某个群的半直积。
文章引用
王钰鑫. 可分解的正则*–半群
On Factorizable Regular*-Semigroups[J]. 理论数学, 2023, 13(07): 1938-1945. https://doi.org/10.12677/PM.2023.137199
参考文献
- 1. Tolo, K. (1969) Factorizable Semigroups. Pacific Journal of Mathematics, 31, 523-535.
https://doi.org/10.2140/pjm.1969.31.523
- 2. Lawson, M.V. (1998) Inverse Semigroups, the Theory of Partial Symmetries. World Scientific, New York.
https://doi.org/10.1142/3645
- 3. Chen, S.Y. and Hsieh, S.C. (1974) Factorizable Inverse Semigroups. Semigroup Forum, 8, 283-297.
https://doi.org/10.1007/BF02194773
- 4. Tirasupa, Y. (1979) Weakly Factorizable Inverse Semigroups. Semigroup Forum, 18, 283-291.
https://doi.org/10.1007/BF02574193
- 5. Tirasupa, Y. (1979) Factorizable Transformation Semigroups. Semigroup Forum, 18, 15-19.
https://doi.org/10.1007/BF02574171
- 6. FitzGerald, D.G. (2010) Factorizable Inverse Monoids. Semigroup Fo-rum, 80, 484-509.
https://doi.org/10.1007/s00233-009-9177-6
- 7. Howie, J.M. (1995) Fundamentals of Semigroup Theory. Oxford University Press, New York.
- 8. Hartmann, M. (2007) Almost Factorizable Orthodox Semigroups. Semigroup Forum, 74, 106-124.
https://doi.org/10.1007/s00233-006-0618-1
- 9. Nordahl, T.E. and Scheiblich, H.E. (1978) Regular*-Semigroups. Semigroup Forum, 16, 369-377.
https://doi.org/10.1007/BF02194636
- 10. East, J. and Azeef Muhammed, P.A. (2023) A Groupoid Approach to Regular*-Semigroups. arXiv:2301.04845v1






 。另一方面,有
。另一方面,有 。故由引理2.1(3)知
,
。于是
。
。故由引理2.1(3)知
,
。于是
。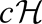 。由(1)和引理2.1(4)知
。记
,其中
。则由
知
。类似可证
。故
,从而
。这表明
。于是
。
。由(1)和引理2.1(4)知
。记
,其中
。则由
知
。类似可证
。故
,从而
。这表明
。于是
。 ,
,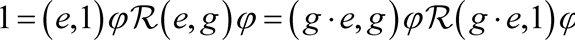 . (3.1)
. (3.1) ,即
,即 ,于是
。
,于是
。