Applied Physics
Vol.08 No.02(2018), Article ID:23801,9
pages
10.12677/APP.2018.82014
The Charged Distribution on the Surface of a Conductor under the Action of the Charged Linear Body
Qili Liao, Ya Deng, Yan Yu
College of Mobile Telecommunications, Chongqing University of Posts and Telecom, Chongqing

Received: Feb. 4th, 2018; accepted: Feb. 19th, 2018; published: Feb. 26th, 2018

ABSTRACT
The charged distribution on the surface of the ground infinite conductor plane and the conductor ball is calculated under the action of the uniformly charged linear body with the superposition principle and Mathematica software. At the same time, the induced charge distribution changing with angle and distance of the image is drawn.
Keywords:Charged Density Distribution, Uniform Charged Linear Body, Infinite Conductor Flat, Conductor Ball, Mathematica
带电线状体作用下的导体表面电荷分布
廖其力,邓娅,余艳
重庆邮电大学移通学院,重庆
收稿日期:2018年2月4日;录用日期:2018年2月19日;发布日期:2018年2月26日

摘 要
本文采用电磁学理论中的镜像法,利用叠加原理和Mathematica数学软件,计算了均匀带电线状体附近的接地无限大导体平面和带电导体球上的感应电荷分布,同时绘出了感应电荷分布随角度和距离变化的图像。
关键词 :电荷分布密度,接地无限大导体平面,导体球,均匀带电线状体,Mathematica

Copyright © 2018 by authors and Hans Publishers Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/


1. 引言
导体表面的电荷分布情况不仅与导体表面的形状有关,还与周围带电体的形状、距离和电量等因素有关,许多文献给出的都是定性描述 [1] [2] [3] [4] ,且大多是由实验来作定性研究。但对于特殊形状的导体,如接地无限大导体平面、导体球等,当它周围是一些形状规则的带电体(线状体)时,利用电磁学中的镜像法和数学计算软件 [5] [6] [7] ,导体表面电荷的分布就可作定量研究。本文基于电磁学理论中的镜像法,运用电场的叠加原理和Mathematica数学软件,分别计算均匀带电线状体作用下在接地无限大导体平面和导体球表面上产生的感应电荷的分布,给出解析结果,同时绘出电荷面密度随角度和距离变化的图像。
2. 均匀带电线状体在接地导体平面上产生的感应电荷分布
当导体置于电场中处于静电平衡时,其表面上的电场强度按电磁场理论为 [1] [2] [3] [4] ,其中 为电荷面密度, 为真空中的介电常数, 为该处外法线单位矢量。则该处的电荷面密度大小为 。下面先考虑电场为点电荷的情况。
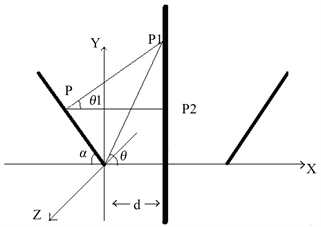
如图1(a)所示,设位于坐标原点 的点电荷 带正电量为 ,它到时无限大接地导体平面的距离为 ,则在导体平面上产生的感应负电荷为 , 轴正方向垂直于导体平面向右。按电磁理论中的镜像法,点电荷 与导体平面上的感应电荷 在导体平面左侧空间产生的作用效果(包括力学的和电磁学的)等效于该点电荷经导体平面成像于 处的负点电荷 共同产生的效果。由此,在导体平面上任一点 处的电场强度大小为 [2] [3] :

 (a)(b)
(a)(b)
Figure 1. Inductive charge distribution in the plane of a grounded conductor. Grounding conductor plane around the point charge; (b) Grounding conductor plane around a charged linear body
图1. 带电体在接地导体平面产生的感应电荷分布。(a) 点电荷周围的接地导体平面;(b) 带电线状体周围的接地导体平面
(1)
其中 ( )为 连线与 轴的夹角,逆时针方向为正。该 处感应负电荷面密度大小为:
(2)
接下来计算均匀带电线状体在导体平面产生的电荷面密度分布情况。建立如图1(b)所示的笛卡尔直角坐标系,设均匀带电线状长 ,均匀带正电为 ,它离导体平面最近的端点为坐标原点 ,垂直于导体平面向右为 轴正方向, 轴在 轴与线状体所决定的平面内, 轴与 、 轴满足右手螺旋系。坐标原点到导体平面的距离为 ,设线状体与 轴负方向夹角为 ,在线状体任取一点 (其中 ),过该点作导体平面的垂线交平面于 点,在导体平面上任取一点 ,其中 角是 连线 轴正方向夹角,称其极角; 角是 点在 平面上的投影点与坐标原点的连线与 轴正方向夹角,称其方位角。则 连线与 的夹角 的余弦值可由立体解析几何中位矢 与 的点积给出,这里的 、 、 分别是 、 、 轴正方向的单位矢。夹角 的余弦值为:
(3)
在 处取一个微元电荷 ,其中 ,当导体平面处于静电平衡时,它在 的产生的感应负电荷面密度大小为:
(4)
其中 ,对 根式中表达式进行展开化简,令 ,则可化为 ,由(4)式可以看出,当导体平面上任
一点
确定,既
、
确定,线状体上任一点
在导体平面上
点处产生的电荷面密度只与
是有关,既利用了电场的叠加原理(在数学上是积分),
将 代入(4)式,对变量
关于(4)式积分,可得出均匀带电线状体在导体平面上
处产生的感应负电荷面密度大小:
代入(4)式,对变量
关于(4)式积分,可得出均匀带电线状体在导体平面上
处产生的感应负电荷面密度大小:
(5)
由此可以看出现,导体平面上任一处的感应负电荷面密度跟均匀带电线状体自体的特征量(电量 和长度 )有关,还跟它与导体平面的相对位置(距离 、夹角 、极角 和方位 )有关。
由(5)式可验证导体平面上总的感应负电荷量大小:
给出两种特殊情况下导体平面上的感应负电荷面密度分布:
A当 时,既均匀带电线状体与导体平面垂直,可得:
(6)
当 较小时,可将(6)式中的根式函数按 用泰列级数展开,得到:
(7)
将(7)式代入(6)式,当 ,这时线状体变为点电荷,其电荷面密度为(2)式。
B当 时,既带电线状体与导体平面平行,可得:
(8)
同样当 较小时,可将(8)式中的函数按 用泰列级数展开,得到:
将上式代入(8),当 ,线状体变为点电荷,(8)式变为(2)式。
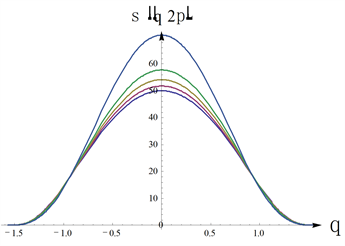
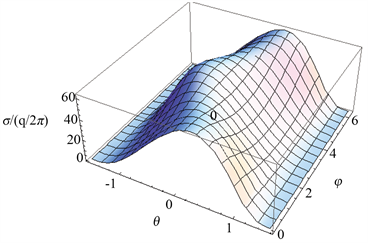
为了直观形象展示导体平面上感应负电荷的分布规律,绘出了均匀带电线状体作用下导体平面处于静电平衡时,其表面上的感应负电荷面密度随距离和角度变化而变化的图像。在图2中,参数取如下值: , ;(a) 图中是方位角 的情况,既是 所决定的平面与导体平面( )的相交直线处电荷密度随角 而变化的情况;(b) 图是在 平面与导体平面( )的交直线上电荷密度随角 而变化。在这两个图中,在第一象限内的图线自下而上分别对应 的情况;从这两个图中可以看出,在带电线状体自体特征量( 、 )及与导体平面相对位置( 、 )确定时,电荷密度分布与极角 和方位角 有关,且随极角 增大而减小且趋于零,仅当 时,既线状体与导体平面垂直,电荷面密度只与极角 有关,与方位角 无关。的图(c)、(d)分别是 、 时电荷密度随角 和 而变化的三D图像。这四个图都清楚表明,电荷面密度随极角 增大而减小且趋于零。
3. 均匀带电线状体作用下的导体球表面上电荷分布
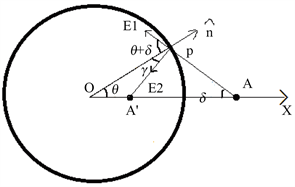
如图3(a)所示,设导体球(或球壳)半径为 ,球心处为坐标系的原点,在 轴上的点电荷 ( )带正电为 ,导体球处于静电平衡时其表面上产生的感应负电荷为 ,点电荷 与球面上的感应负电荷在球外空间产生的作用效果等效于该点电荷经球面成像于 处的负点电荷 和该点电荷共同在导体球外空间产生的作用效果,其中 、感应电荷量为 [3] 。当导体球接地时,点电荷 和像点电荷 在导体球表面上任一点 处感应负电荷面密度大小由 有:
(9)
其中 、 分别是点电荷 和像点电荷 在导体球表面点 处产生的电场强度, 是点电荷 和像点电荷 在导体球表面点 处产生的合场强; 是 连线与 轴正方向的夹角; 是 连线
 (a)
(a)
 (b)
(b)
 (c)
(c)
 (d)
(d)
Figure 2. Distribution of induced charge varies with angles. (a) Distribution of induced negative charge varies with different angles ( ); (b) Distribution of induced negative charge density varies with different angles ( ); (c) Distribution of induced negative charge varies with and ( ); (d) Distribution of induced negative charge density varies with and ( )
图2. 导体平面上的电荷密度随角度的变化。(a) 当 时 随角 而变化;(b) 当 时 随角而变化;(c) 当 时 随角 和 而变化;(d) 当 时 随角 和 而变化
 (a)
(a)
 (b)
(b)
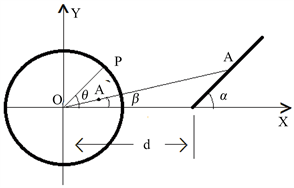
Figure 3. Charged body and charged conductor ball. (a) Point charge and charged conductor sphere; (b) Uniform charged linear and conductor spheres
图3. 带电体与带电导体球。(a) 点电荷与带电导体球;(b) 均匀带电线状体与导体球
与 轴负方向的夹角, 是 连线与 连线的夹角;利用三角形的正、余弦定理将
、 、 、 代入(9)式,其中 、 。由此可得:
(10)
由 、 可证明:
(11)
即可验证 处的电场强度只有法线分量,其切线分量为零,即处于静电平衡时其电场度与表面(等势面)垂直。由(10)式也可验证导体球上感应电荷量为:
(12)
当导体球所带净电荷为零且不接地时,由独立作用原理和叠加原理导体球面可知,感应正电荷在导体球表面上的分布具有球对称性,它在球外空间(包括球面上)产生的作用效果等效于等量正点电荷 位于球心处在球外空间产生的作用效果。则导体球面任一点 处感应电荷面密度大小为:
(13)
接下来研究在均匀带电线状体作用下导体球表面的电荷分布密度。
如图3(b)所示,设半径为 的导体球的球心为坐标系的坐标原点,球心与线状体最近一端的端点的连线为 轴,线状体最近一端到球心的距离为 ,与 轴正方向的夹角为 , 轴在 轴与均匀带正电量为 、长为 的线状体所决定的平面内,由于导体球表面上感应电荷分布只与极角 有关,与方位角 无关,故只选择用二维坐标系 就足以描述感应电荷分布。在线状体上任一点 处取一微元电荷 ,由电磁理论中的镜像法,该电荷在导体球产生的感应负电荷(像)的位置 ,其中 , 是 与 轴的夹角,感应负电荷的电量 。则该微元电荷 在导体表面上任一点 产生感应负电荷面密度大小由(10)式有:
(14)
其中 是 与 轴正方向的夹角。由三角形正余弦定理有 、 、 ,将它们代入(14)式,再令 和 ,(14)式可化为下式:
(15)
由(15)式可以看出,当导体球上任一点 确定,既 确定,线状体上任一点 在导体球上 点处产生的电荷面密度是 的函数,利用了电场的叠加原理,既对(15)式中的变量 积分,再将 、 代入后可得到在导体球表面上感应负电荷的电荷面密度大小分布:
(16)
由(16)式可以看出现,导体球表面上的感应负电荷面密度跟均匀带电线状体的电量 和长度 有关,还跟它与导体球表面的距离 、夹角 和极角 有关。
当 时,既线状体的延长线通过导体球的球心,导体球表面上电荷分布:
(17)
当 时,可将(17)式中的根式和对数函数按 用泰列级数展开,得到:
将上式代入(17)式,当 时,再将 换成 ,这时均匀带电线状体就是变为点电荷,于是(17)式变为点电荷对应的(10)式。
均匀带电线状体在导体球上产生的感应电荷量为:
(18)
当 时,可将(18)式中的对数函数按 级数展开,当 时,带电线状体的(18)式就变为点电荷对应的(12)式。
也可从(16)式得到相同的结果:
当不接地导体球带净电荷为 时,同样由独立作用原理和叠加原理可知,电荷 和感应正电荷 在导体球表面上的分布具有球对称性,它们在球外空间(包括球面上)产生的作用效果等效于在球心处等量点电荷 在球外空间产生的效果。其表面的电荷面密度的分布为:
(19)
其中 、 分别为(16)式和(18)式。
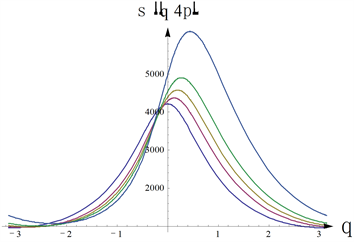
为了直观展示均匀带电线状体作用下在导体球表面上产生的感应电荷分布情况,图4给出了感应电荷面密度随距离 、极角 和夹角 的分布规律。在这四个图中,相同参数选择取为 、 。图4(a)为导体球接地,线状体最近端与球心连线与 轴正方向的夹角 在不同角度时导体球上的感应负电荷面密度大小随 分布的情况,其中 ,图线自上而下分别对应于夹角为 的情况,从图线可看出,仅当 ,既带电线状体的延长线通过导体球心,电荷面密度分布才具有 轴的对称性,但这些图线都反映了电荷面密度随着极角 的增大而减小但不趋于零。
 (a)
(a)
 (b)
(b)
 (c)
(c)
 (d)
(d)
Figure 4. Charge distribution on the surface of a conductor sphere. (a) Distribution of induced negative charge with different angles; (b) Distribution of induced negative charge density varies with different distance and angles; (c) Distribution of induced charge density varies with different angles; (d) Distribution of induced charge density with different distance and angles
图4. 导体球表面上的电荷分布。(a) 感应负电荷密度在不同夹角时随 的分布;(b) 感应负电荷密度随 和 的分布;(c) 电荷密度在不同夹角时随 的分布;(d) 电荷密度随 和 的分布
图4(b)为导体球接地,线状体近端与球心连线夹角为 时感应负电荷大小随距离 和极度 分布的三维情形。图4(c)为导体球净电荷为零且不接地,线状体近端与球心连线在不同夹角时导体球表面感应(正、负)电荷随 分布的情况,其中 ,第四象限的图线自上而下分别对应于夹角为 的情形,这些图线显示:在第一、二象限内感应电荷面密度为正的表示在这些区域出现感应净的正电荷,由独立作用原理可以理解为感正电荷具有球对称性,之所以出现净的正感应电荷,是该处感应负电荷分布相对较少,叠加(中和)后表现为正,表明感应电荷为(净)正的区域出现在极度 相对较大的区域,既远离带电线状体的地方;同理在第三、四象限内感应负电荷出现在极度 相对较小的区域,既离带电线状体相对近的地方;出现感应电荷面密度为零的地方是该处感应正、负电荷面密度相等,叠加(中和)后为零。图4(d)为导体球净电荷为零且不接地,线状体近端与球心连线与 轴夹角为 时感应(正、负)电荷导体球表面随距离 和角度 分布的三维情形。
4. 结束语
本文基于电磁场理论中的镜像法,借助于Mathematica研究了均匀带电线状体作用下接地无限大导体平面和带电导体球表面的电荷密度分布,给出了解析表达式,并绘出电荷密度随距离和角度变化而变化的图像。虽然均匀带电线状和无限大导体平面只是理想模型,但当带电棒的长度远大于其直径时可近似为线状体;当导体平面尺寸远大于带电棒长度且距离导体平面足够近时,也可视为无限大导体平面,知道了电荷面密度由 就可得到该处的电场强度。故以上的研究可作为实际情况的一种近似,它的研究具有一定的理论价值和实际意义。
文章引用
廖其力,邓 娅,余 艳. 带电线状体作用下的导体表面电荷分布
The Charged Distribution on the Surface of a Conductor under the Action of the Charged Linear Body[J]. 应用物理, 2018, 08(02): 116-124. http://dx.doi.org/10.12677/APP.2018.82014
参考文献 (References)
- 1. 赵凯华, 陈熙谋. 电磁学(上) [M]. 北京: 高等教育出版社, 1985: 127-146.
- 2. 梁灿彬, 秦光戎, 梁竹健. 电磁学[M]. 北京: 高等教育出版社, 1980: 64-86, 104-106.
- 3. 郭硕鸿. 电动力学[M]. 北京: 高等教育出版社, 1979: 71-76.
- 4. 谢国亚, 林朝金, 廖其力. 大学物理教程(下) [M]. 长春: 吉林大学出版社, 2012: 31-36.
- 5. 廖其力, 余艳, 邓娅, 邓敏艺, 白克钊. 用Mathematica研究环形电流平面内磁场[J]. 广西物理, 2016, 37(1): 54-56.
- 6. 杨天虎. 两共轴带电圆环作用力的计算[J]. 大学物理, 2016, 35(8): 29-31.
- 7. 王福谦, 贾兰芳, 王磊. 接地条形体板对均匀电场的影响及其数值模拟[J]. 大学物理, 2017, 36(2): 36-38.