Applied Physics
Vol.
12
No.
06
(
2022
), Article ID:
52702
,
8
pages
10.12677/APP.2022.126040
一种基于半圆形开口谐振环结构的太赫兹环偶极子超表面设计
王晨,王爽*
天津职业技术师范大学电子工程学院,天津
收稿日期:2022年5月13日;录用日期:2022年6月15日;发布日期:2022年6月22日

摘要
设计了一种基于半圆形开口谐振环结构太赫兹环偶极子谐振的超表面,超表面的单元结构由金属结构层及基底介质组成。金属结构层由一对对称半圆形开口谐振环和一个矩形金属条构成。利用电磁仿真软件研究了半圆形半径r及开口距离d对超表面谐振频率、品质因子Q值等电磁特性的影响;通过计算超材料多极子的散射功率研究内部机理。发现超表面的谐振响应随着半径和开口间距的改变而发生变化;该设计实现了一种新型太赫兹波段的平面环偶极子超表面,为太赫兹功能器件的开发和应用提供了更多的可能性。
关键词
超表面,环偶极子,半圆形开口谐振环,太赫兹波

Terahertz Toroidal Dipole Metasurface Design with Split Semiring Resonator Structure
Chen Wang, Shuang Wang*
School of Electronic Engineering, Tianjin University of Technology and Education, Tianjin
Received: May 13th, 2022; accepted: Jun. 15th, 2022; published: Jun. 22nd, 2022

ABSTRACT
A metasurface based on Terahertz (THz) toroidal dipole resonance of split semi-ring resonator structure is designed. The unit structure of metasurface consists of a pair of symmetric semicircular split ring, a metal strip and a substrate medium. The influence of the change of semicircular radius (r) and opening distance (d) on the electromagnetic characteristics of metasurfaces such as resonance frequency and quality factor (Q) was investigated by using the electromagnetic simulation software. It is found that the resonant response of the metasurface varies with the radius (r) and the spacing gap between split semiring. The design implements a new terahertz band planar toroidal dipole metasurface, which provides more possibilities for the development and application of terahertz functional devices.
Keywords:Metasurface, Toroidal Dipole, Semicircle Split Ring Resonator, Terahertz Band

Copyright © 2022 by author(s) and Hans Publishers Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY 4.0).
http://creativecommons.org/licenses/by/4.0/


1. 引言
经典电动力学中,通常有电多极子和磁多极子两大多极子系统 [1]。而作为第三类辐射源的环偶极子,虽然是通过电多极子或磁多极子相干作用产生,但却具有与众不同的特性。环偶极子的概念于1957年提出,也被称作“Anapole” [2]。环偶极子可等效为多个磁偶极子首尾相连围成的一个环形结构 [3]。由于在自然界中常被电多极子和磁多极子所掩盖,环偶极子的研究一直没有显著进展,但超材料的出现为环偶极子的研究提供了有效手段。超材料可以通过人工设计,用来实现自然材料所不具备的电磁特性 [4] [5] [6]。材料的介电常数反映了单元对外加电场的响应,磁导率反映了单元对外加磁场的响应。通过设计超材料阵列的结构和大小,我们可以改变它的ε和μ [7]。其中具有二维结构的超材料,称之为超表面(metasurface)。为了后续方便器件化,本设计采用超表面二维结构。目前,超材料已应用于对环偶极子电磁响应特性的研究之中。从微波波段开始,随后研究光波波段环偶极子超材料直至延伸至太赫兹波段环偶极子超材料。通过设计超材料的单元结构,增强环偶极子谐振强度同时抑制其他谐振,使得环偶极子谐振达到可观测范围,超材料为研究环偶极子机制提供了有效的研究手段 [8] [9] [10] [11]。2015年天津大学的丁春峰从品质因子Q值的角度入手,在太赫兹频段仿真分析并通过测试验证了若干具有较高Q值的稳定结构的环偶极子超材料,讨论了高Q值背后的共振特性 [12]。2018年天津职业技术师范大学的王爽等设计并加工了一种柔性二维平面结构的太赫兹环偶极子超材料,在理论分析和数值计算上证明了这种环偶极子共振也可以产生于简易的二维平面结构超表面中。本文通过对二维环偶极子超表面单元结构的设计,来研究太赫兹波段环偶极子的产生原理。超表面微结构由三个谐振耦合而成。超表面单元结构采用半圆形开口环结构,两个半圆形开口谐振环沿xoz平面对称,金属谐振条位于x轴上。然后利用CST MICROWAVE STUDIO (CST)软件进行电磁仿真,对环偶极子超表面的结构及电磁特性及电磁场以及电流分布情况进行分析,同时计算超表面多极子的散射功率,用于研究环偶极子的特性和内部机理。
2. 超表面的单元结构
开口谐振环(SRR)是构成环偶极子超材料的最基本的模型结构之一,在滤波器、吸波器等领域有着广泛的应用。开口谐振环最经典的形式是在高导电性能的金属环上打开一个或几个开口间隙,开口间隙往往由空气或者其它介电材料充当。在外加时变电磁场的条件下,开口谐振环将会在其金属环上激发出环形的表面电流,电荷将聚集在开口处。本文结构是在SRR的基础上设计而来。
图1为基于半圆形开口谐振环结构的环偶极子超表面的单元结构。该单元结构由金属层和介质层组成,金属层包括两个半圆形金属环及矩形金属条,其中上下两个开口金属环关于xoz平面对称。矩形开口环的金属材料为铝,铝具有焦耳损耗小的特点,可以减少金属的非辐射损耗。介质基底材料为聚酰亚胺(polyimide),该材料的介电性能良好,在太赫兹频段具有高透射率、低损耗等特性。半圆形开口谐振环超表面的单元结构尺寸,分别是单元结构的周期长、宽a × a = 328 μm × 328 μm,金属环的外径r = 60 μm,金属条长度b = 224 μm,金属条宽度、金属环宽度均为w = 6 μm,开口间距d = 12 μm;超表面的金属环的厚度为0.2 μm。基底介质厚度为20 μm。在空间中,单元结构呈周期性排列,形成二维周期阵列,构成了半圆形开口谐振环的超表面结构。

Figure 1. Schematic diagram of metasurface element structure
图1. 超表面单元结构示意图
3. 基于半圆形开口谐振环结构的环偶极子超表面的电磁仿真与分析
本实验采用CST软件实现超表面的结构设计并对其进行太赫兹频段的电磁性能仿真。在CST软件系统中设计构造出半圆形开口环环偶极子超表面的单元结构,并设置好相应的材料特性及尺寸参数,如图1所示。设置仿真频率范围为0~1.2 THz,电磁波沿Z轴射入,电场沿X轴极化,磁场的方向沿着Y轴。基于上述结构的设计,接下来利用CST软件对其进行时域仿真,得到THz频段的透射曲线,并在谐振处进行磁场和表面电流的仿真分析。图2是基于半圆形开口谐振环结构的超表面的透射曲线,观察到曲线有两个谐振点,分别位于0.35 THz和0.46 THz处,我们将其称为低频谐振点和高频谐振点。当两个谐振点的距离较为接近时,会产生电磁感应透明(EIT)效应。EIT效应是原子物理中一种非常重要的物理现象 [13] [14]。一般情况下,当两个共振发生相干耦合时,破坏性干涉会抑制较宽的共振,产生一个诱导的透明窗口。EIT效应由亮模和暗模耦合产生,其中亮模是具有较高辐射损耗的超辐射态,暗模是具有高Q值的次辐射态 [15] [16]。当频率为0.35 THz时,环偶极子的Q值为25。当频率为0.46 THz时,环偶极子的Q值为33。两个相邻环偶极子共振的耦合干扰最终形成类EIT现象 [17] [18] [19] [20]。
低谐振频率点和高频谐振点表面电流和磁场的分布如图3所示。观察超表面的电流分布,可以看出在外加电磁辐射的作用下,在金属环的表面形成电流环,电流绕着两金属环流动。由图3(a)可知,金属结构上半部分电流逆时针流动,从而形成一个指向Z轴正方向的磁偶极子;下半部分电流顺时针流动,从而形成一个指向Z轴负方向的磁偶极子。这一对磁偶极子,相互耦合,最终形成了图3(b)所示的沿着x轴方向的环偶极子。同时可以发现,图3(a)中,金属条电流沿x轴正方向,根据右手定则,可产生环形
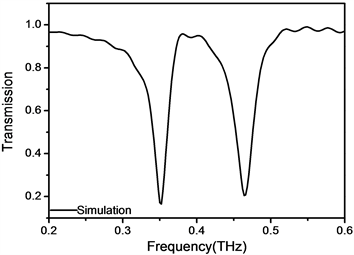
Figure 2. Transmission curve of metasurface based on semicircular resonant ring structure
图2. 基于半圆形开口谐振环结构的超表面的透射曲线
磁场。磁场在xoy平面中,y大于零区域沿z轴正方向,y小于零区域沿z轴负方向,与之前两个半圆形开口谐振环磁场方向一致,对环偶极子起到增强作用。
由图3(c)可知,金属结构上半部分电流逆时针流动,从而形成一个指向Z轴正方向的磁偶极子;下半部分电流顺时针流动,从而形成一个指向Z轴负方向的磁偶极子。这一对磁偶极子,相互耦合,最终形成了图中3(b)所示的沿着x轴方向的环偶极子。同时可以发现,图3(b)中,金属条电流沿x轴正方向,根据右手定则,可产生环形磁场,磁场在xoy平面,y大于零区域沿z轴负方向,y小于零区域沿z轴正方向,与之前两个半圆形开口谐振环磁场方向相反,对环偶极子起到减弱作用。比较图3(a)和图3(b)可以观察到图3(b)图环偶极子强度弱于图3(a)图环偶极子强度。
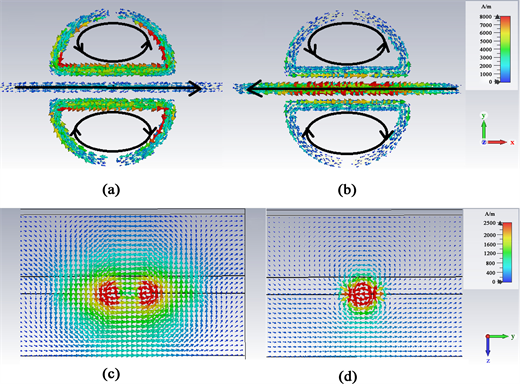
Figure 3. (a) Low-frequency surface current distribution; (b) Low-frequency magnetic field distribution; (c) High-frequency surface current distribution; (d) High-frequency magnetic field distribution
图3. 金属结构超表面(a) 低频表面电流分布;(b) 低频磁场分布;(c) 高频表面电流分布;(d) 高频磁场分布
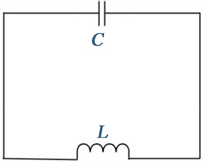
超表面上下两部分由完全对称半圆形开口谐振环组成,在不考虑金属条的情况下,我们根据开口谐振环的LC等效谐振电路,研究超表面的电磁特性。图4(a)是低频谐振的等效电路,它由一个等效电容和等效电感组成,其中等效电容来自于谐振环的开口,等效电感来自金属环本身的自感效应,这样我们可以用公式(1)来描述谐振的频率 [21]:
(公式1)
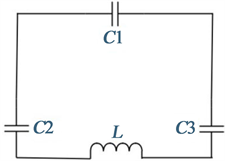
同时,在高频谐振处,等效电感同样来自金属环自身的自感效应,而等效电容来自三个地方,分别是金属环的开口间距以及金属环左右两边相反方向表面电流连接处,其中对谐振影响起主要作用的依然是开口间距。高频谐振处的等效电路如图4(b)所示,其中C1代表开口间距处的等效电容,C2和C3代表金属环左右两边相反方向表面电流连接处的等效电容。高频谐振处的谐振频率可以用公式(2)表示:
(公式2)
 (a)
(a)
 (b)
(b)
Figure 4. Resonant open ring equivalent circuit model. (a) Low-frequency resonant equivalent circuit; (b) High-frequency resonant equivalent circuit
图4. 谐振开口环等效电路模型。(a) 低频谐振等效电路;(b) 高频谐振等效电路
4. 环偶极子超表面的数据分析
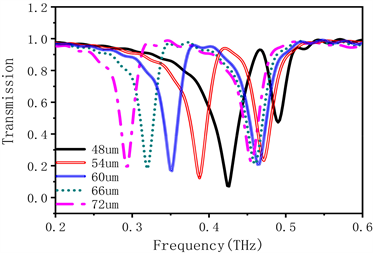
下面分析结构参数外径r对谐振的影响。在保持其他参数不变的情况下只改变两个半圆环的外径r = 48 μm、r = 54 μm、r = 60 μm、r = 66 μm、r = 72 μm、r = 78 μm。通过仿真和计算我们得到了不同r情况下的超表面透射曲线,如图5(a)所示。随着r增大,低频谐振点向低频移动,变化范围较大,从0.425 THz移动到0.3 THz;同时,低频谐振点的透射系数略有减小,从0.18到0.03。随着r增大,高频谐振点向低频移动,变化范围较小,从0.48 THz移动到0.46 THz;透射系数逐渐减小,从0.43到0.2。可以看出随着外径r的增大,无论是低频谐振还是高频谐振都发生不同程度的红移。在低频谐振处,根据公式(1)来解释,当谐振环的外径增大时,开口处的等效电感随之增大,而等效电容基本不发生变化,这就导致了谐振的频率减小,低频谐振产生红移。同样地,对于高频谐振,根据公式(2),当谐振环的外径增大时,等效电感增大,而等效电容基本不发生变化,这样谐振频率也会减小,在高频谐振处产生红移现象。
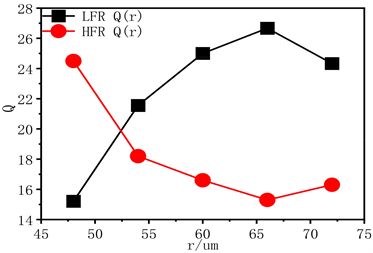
图5(b)为低频高频谐振点Q值随半径r变化曲线。随着外径r的增大,低频谐振的Q值逐渐增大,超表面的非辐射损耗随之减小;r = 66 μm时达到峰值26.7,当r进一步增大时Q值开始减小。随着外径r的增大,高频谐振的Q值逐渐减小,超表面的非辐射损耗随之增大;r = 66 μm时达到最小值15.3,当r进一步增大时Q值略有增大。高Q环偶极子超表面有助于制备高效的超表面功能器件。
 (a)
(a)
 (b)
(b)
Figure 5. (a) Transmission curve and (b) Q value of the metasurface of semicircular resonant structure with different outer diameters r
图5. 不同外径r的半圆形开口谐振结构超表面。(a) 透射曲线;(b) Q值
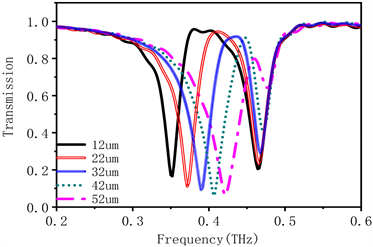
接下来研究开口间距d对半圆形开口谐振环结构的超表面电磁特性的影响。保持其他参数不变,改变开口间距d = 12 μm、22 μm、32 μm、42 μm、52 μm。通过仿真和计算我们得到了不同开口间距d情况下的超表面透射曲线,如图6(a)所示。
在图6(a)中,我们可以观察到随着开口间距d的增大,低频谐振点向高频移动,频率从0.35 THz逐渐蓝移至0.42 THz。由公式(2)可知 [22],随着开口距离d的增大,等效电容随之减小,同时金属环的长度减小导致等效电感的减小,最终谐振频率随之增加。同时,随着d增大低频谐振点的透射系数略有减小,从0.15到0.05。高频谐振点没有明显位移,但其透射系数逐渐增大,从0.2到0.62。图6(b)为低频谐振点的Q值变化曲线。随着开口间距d的增大,低频谐振的Q值逐渐减小,超表面的非辐射损耗随之增大,d = 42 μm时达到最低点13.5,当d进一步增大时Q值增大。随着开口间距d的增大,高频谐振的Q值逐渐增大,超表面的非辐射损耗逐渐减小,d = 52 μm时达到最大值26.6。
 (a)
(a)
 (b)
(b)
Figure 6. (a) Transmission curve; (b) Q value of the metasurface of semicircular resonant structure with different outer diameters R
图6. 不同外径r的半圆形开口谐振结构超表面。(a) 透射曲线;(b) Q值
为了进一步研究超表面透射光谱中两个谐振的机理,根据多极矩理论 [23] [24],我们计算了谐振系统中多极子的散射功率。电偶极子Px沿x轴,磁偶极子Mz沿z轴,环形偶极子Tx沿x轴。图7给出了等效状态下的超表面多极子散射功率图。环形偶极子的散射功率比其他多极子高几个数量级,这说明环偶极子在0.2~0.8 THz是主要谐振。同时,在散射功率曲线的变化趋势上,环形偶极子与磁偶极子基本相同,这与上面关于磁偶极子耦合形成环形偶极子的讨论是一致的。

Figure 7. Scattering power of a metasurface multipole
图7. 超表面多极子的散射功率
5. 结论
本文提出一种基于半圆形开口谐振环结构的太赫兹环偶极子超表面。通过电磁仿真软件CST进行超表面电磁特性的时域仿真,研究超表面电磁特性,分析了超表面的表面电流及磁场分布。环偶极子超表面在0.2~1.2 THz呈现低频和高频两个谐振峰,并且产生类EIT效应。在太赫兹波的作用下,上下两侧产生方向相反的磁偶极子,磁偶极子首尾连接相互耦合实现了环偶极子的电磁响应。通过计算超材料多极子的散射功率,证明了环偶极子的存在。研究r、d对电磁特性的影响。随着r增大,低频谐振点向低频移动,变化范围较大,从0.425 THz移动到0.3 THz。高频谐振点向低频移动,变化范围较小,从0.48 THz移动到0.46 THz。随着r的增大,低频谐振的Q值逐渐增大,最终达到最大值26.7;高频谐振的Q值逐渐减小,最小值为15.3。随着d增大,低频谐振点向高频移动,频率从0.35 THz逐渐蓝移至0.42 THz,Q值逐渐减小直至最小值13.5;高频谐振的Q值逐渐增大,最终达到最大值26.6。本文所设计的结构在两个谐振峰均有环偶极子,且在低频谐振处可以得到高Q值26.7。高Q值是超表面高性能的体现,有利于高性能太赫兹功能器件的研发。根据麦克斯韦公式可知,此设计超材料可以用于微波和光波频段。
基金项目
利用近场增强实现基于石墨烯和超材料复合结构的可调谐非线性太赫兹调制器件(国家自然科学基金61705167);太赫兹实时可编程超材料器件研究(天津市教委科研计划项目2020KJ125)。
文章引用
王 晨,王 爽. 一种基于半圆形开口谐振环结构的太赫兹环偶极子超表面设计
Terahertz Toroidal Dipole Metasurface Design with Split Semiring Resonator Structure[J]. 应用物理, 2022, 12(06): 343-350. https://doi.org/10.12677/APP.2022.126040
参考文献
- 1. 郭林燕. 环形偶极子超介质的实现与特性研究[D]: [博士学位论文]. 武汉: 华中师范大学, 2016.
- 2. 王爽, 李泉, 王晨. 环偶极子研究现状与太赫兹频段应用展望[J]. 天津职业技术师范大学学报, 2016, 26(4): 28-31+35.
- 3. 李珍珍. 基于磁环偶极子的双频高Q值电磁波超材料的设计研究[D]: [硕士学位论文]. 南京: 南京航空航天大学, 2016.
- 4. O’Hara, J.F., Singh, R., Brener, I., Smirnova, E., Han, J., Taylor, A.J., et al. (2008) Thin-Film Sensing with Planar Terahertz Metamaterials: Sensitivity and Limitations. Optics Express, 16, 1786-1786. https://doi.org/10.1364/OE.16.001786
- 5. Dong, Z.G., Zhu, J., Rho, J., Li, J.-Q., Lu, C., Yin, X.B., et al. (2012) Optical Toroidal Dipolar Response by an Asymmetric Double-Bar Meta material. Applied Physics Letters, 101, Article ID: 144105. https://doi.org/10.1063/1.4757613
- 6. Smith, D.R., Pendry, J.B. and Wiltshire, M.C. (2004) Metamaterials and Negative Refractive Index. Science, 305, 788-792. https://doi.org/10.1126/science.1096796
- 7. Song, S., Yu, S., Li, H. and Zhao, T. (2022) Ultra-High Q-Factor Toroidal Dipole Resonance and Magnetic Dipole Quasi-Bound State in the Continuum in an All-Dielectric Hollow Metasurface. Laser Physics, 32, Article ID: 025403 (8 p). https://doi.org/10.1088/1555-6611/ac46cf
- 8. Carletti, L., Zilli, A., Moia, F., Toma, A., Finazzi, M., De Angelis, C., et al. (2021) Steering and Encoding the Polarization of the Second Harmonic in the Visible with a Monolithic LiNbO3 Metasurface.ACS Photonics, 8, 731-737. https://doi.org/10.1021/acsphotonics.1c00026
- 9. Zubyuk, V., Carletti, L., Shcherbakov, M. and Kruk, S. (2021) Resonant Dielectric Meta-Surfaces in Strong Optical Fields. APL Materials, 9, Article ID: 060701. https://doi.org/10.1063/5.0048937
- 10. Lee, C.W., Choi, H.J. and Jeong, H. (2020) Tunable Metasurfaces for Vis-ible and SWIR Applications. Nano Convergence, 7, Article No. 3. https://doi.org/10.1186/s40580-019-0213-2
- 11. 牧凯军, 张振伟, 张存林. 太赫兹科学与技术[J]. 中国电子科学研究院学报, 2009, 4(3): 221-230+237.
- 12. 丁春峰. 高Q值共振的太赫兹超材料研究[D]: [博士学位论文]. 天津: 天津大学, 2015.
- 13. Boller, K.J., Imamo, L.A. and Harris, S.E. (1991) Observation of Electromagnetically Induced Transparency. Physical Review Letters, 66, 2593-2596. https://doi.org/10.1103/PhysRevLett.66.2593
- 14. Abdelwaheb, O., Bruno, G., Loic, B., De Rosny, J. and Dahoo, P.R. (2015) Electromagnetically Induced Transparency in Symmetric Planar Metamaterial at THz Wave-lengths. Photonics, 2, 308-316. https://doi.org/10.3390/photonics2010308
- 15. Luk’Yanchuk, B., Zheludev, N.I., Maier, S.A., Halas, N.J., Nord-lander, P., Giessen, H., et al. (2010) The Fano Resonance in Plasmonic Nanostructures and Metamaterials. Nature Mate-rials, 9, 707-715. https://doi.org/10.1038/nmat2810
- 16. Liang, D., Zhang, H., Gu, J., Li, Y., Tian, Z., Ouyang, C., et al. (2017) Plasmonic Analog of Electromagnetically Induced Transparency in Stereo Metamaterials. IEEE Journal of Selected Topics in Quantum Electronics, 23, Article No. 4700907. https://doi.org/10.1109/JSTQE.2017.2657681
- 17. Han, S., Cong, L., Gao, F., Singh, R. and Yang, H. (2016) Observation of Fano Resonance and Classical Analog of Electromagnetically Induced Transparency in Toroidal Metamaterials. Annalen der Physik, 528, 352-357. https://doi.org/10.1002/andp.201600016
- 18. Dayal, G., Chin, X.Y., Soci, C. and Singh, R. (2016) High-Q Whispering-Gallery-Mode-Based Plasmonic Fano Resonances in Coupled Metallic Metasurfaces at Near Infrared Frequencies. Advanced Optical Materials, 4, 1295-1301. https://doi.org/10.1002/adom.201600356
- 19. Francescato, Y., Giannini, V. and Maier, S.A. (2012) Plasmonic Systems Unveiled by Fano Resonances. ACS Nano, 6, 1830-1838. https://doi.org/10.1021/nn2050533
- 20. Singh, R., Al-Naib, I.A.I., Koch, M. and Zhang, W. (2011) Sharp Fano Resonances in THz Metamaterials. Optics Express, 19, 6312-6319. https://doi.org/10.1364/OE.19.006312
- 21. Ahmadivand, A., Gerislioglu, B., Tomitaka, A., Manickam, P., Kaushik, A., Bhansali, S., et al. (2018) Extreme Sensitive Metasensor for Targeted Biomarkers Identification Using Colloidal Nanoparticles-Integrated Plasmonic Unit Cells. Biomedical Optics Express, 9, 373-386. https://doi.org/10.1364/BOE.9.000373
- 22. 王胜磊. 磁环形矩及其在开口谐振环中的实现与特性研究[D]: [硕士学位论文]. 哈尔滨: 哈尔滨工业大学, 2014.
- 23. Ahmadivand, A., Gerislioglu, B., Ramezani, Z. and Ghoreishi, S.A. (2019) Demonstration of Robust Plexcitonic Coupling in Organic Molecules-Mediated Toroidal Meta-Atoms. Advanced Optical Materials, 7, Article ID: 1901248. https://doi.org/10.1002/adom.201901248
- 24. Ge, L., Liu, L., Dai, S., Chai, J., Song, Q., Xiang, H., et al. (2016) Unidirectional Scattering Induced by the Toroidal Dipole Moment in the System of Plasmonic Nanoparticles. Optics Express, 25, 10853-10862. https://doi.org/10.1364/OE.25.010853
NOTES
*通讯作者。