Computer Science and Application
Vol.07 No.02(2017), Article ID:19839,12
pages
10.12677/CSA.2017.72017
An Improved Artificial Bee Colony Algorithm Based on Hooke-Jeeves Method
Yuehong Sun1,2, Yaying Ding2
1Jiangsu Provincial Key Laboratory for Numerical Simulation Large Scale Complex Systems, Nanjing Jiangsu
2School of Mathematical Sciences, Nanjing Normal University, Nanjing Jiangsu

Received: Feb. 4th, 2017; accepted: Feb. 25th, 2017; published: Feb. 28th, 2017

ABSTRACT
Artificial bee colony algorithm (ABC) is a relatively new swarm intelligence optimization method, which is superior to other population-based intelligent algorithms. However, ABC algorithm also has certain limitation because its updating formula is not good at exploitation. In order to enhance the exploitation capacity of ABC, this paper presents a new algorithm called an improved artificial bee colony algorithm based on Hooke-Jeeves method (IHABC). The altered formulas of employed bees and onlooker bees in IHABC not only keep exploration ability but also increase exploitation to a great extent. In addition, the algorithm optimizes initial base point selection in Hooke-Jeeves search phase by upper-middle individual and modifies step size formula of exploratory move, so that the whole population evolves spontaneously in the right direction. To test the effectiveness of the proposed algorithm, we compare IHABC with ABC and Hooke-Jeeves artificial bee colony algorithm (HABC). The numerical experimental results of 30 benchmark functions clearly indicate that IHABC gets higher approximate solution precision in solving unconstrained optimization problems.
Keywords:Swarm Intelligence, Artificial Bee Colony Algorithm, Hooke-Jeeves Search, Local Exploitation Capacity, Unconstrained Optimization Problems
基于Hooke-Jeeves的改进人工蜂群算法
孙越泓1,2,丁亚英2
1江苏省大规模复杂系统数值模拟重点实验室,江苏 南京
2南京师范大学数学科学学院, 江苏 南京
收稿日期:2017年2月4日;录用日期:2017年2月25日;发布日期:2017年2月28日

摘 要
人工蜂群算法(ABC)是新近提出的一种基于群智能的优化方法,它比其他基于种群的智能算法更优异,但蜂群的搜索更新公式在算法的局部寻优能力上存在缺陷。因此本文致力于将擅长局部寻优的搜索机制引入人工蜂群算法,提出了一种基于Hooke-Jeeves的改进人工蜂群算法(IHABC)。IHABC算法改进了采蜜蜂和跟随蜂的搜索公式,期望保留全局搜索能力的同时能更大限度地增加算法的局部寻优能力;采用质量中上的个体优化Hooke-Jeeves搜索法的初始基点以确保局部寻优的有效性;改进Hooke-Jeeves方法的探索移动的步长公式。为了检测新算法的性能,将其与人工蜂群算法、Hooke-Jeeves人工蜂群算法(HABC)进行比较分析,30个基准函数上的数值实验结果表明,IHABC算法在求解无约束优化问题时得到的近似解有更高的精度。
关键词 :群智能,人工蜂群算法,Hooke-Jeeves搜索,局部寻优能力,无约束优化问题

Copyright © 2017 by authors and Hans Publishers Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/


1. 引言
人工蜂群算法(Artificial Bee Colony algorithm, ABC) [1] [2] 属于智能优化方法之一,由Karaboga和Basturk受蜜蜂觅食行为启发而提出。它以结构简单、应用范围广、表现优异等特点,受到优化领域学者们的关注。但是Zhu和Kwong [3] 指出ABC的搜索公式精于全局搜索,疏于局部寻优。为了改善ABC算法的性能,memetic算法 [4] 将ABC算法与局部寻优方法相结合,充分利用两种算法的优势,即将ABC算法的全局搜索能力贡献给memetic算法,使得它比单用局部寻优方法更不容易陷入局部最优;同时将局部寻优的能力贡献给ABC算法,使得它比单用全局搜索算法能更快地收敛。Bansal等 [5] 在ABC算法中加入黄金分割搜索(Golden Section Search, GSS),提出MeABC算法。Gao等 [6] 将Powell方法与ABC结合提出PABC算法,充分利用ABC的全局搜索能力,将任意选出的个体往当前种群的适应度值最大的个体方向进行略微调整,在调整后的新个体上用Powell方法进行局部寻优。
2011年Kang等 [7] 将Rosenbrock转轴法与原始ABC结合,得到了RABC算法。Kang等 [8] 2013年进一步尝试将Hooke-Jeeves直接搜索方法与人工蜂群算法ABC结合,命名为HABC,其全局搜索阶段与ABC类似,仅将适应度计算公式改为公式(7),并对当前种群中目标函数值最小的个体用Hooke-Jeeves方法进行局部寻优。
本文在HABC基础上,对采蜜蜂和跟随蜂的候选解产生公式做了改动,期望保留全局搜索能力的同时能更大程度地增加算法的局部寻优能力,从而加快算法的收敛速度。另外,对Hooke-Jeeves方法的初始基点进行优化,提高局部寻优的有效性并避免其陷入局部最优。数值实验表明提出的新算法在求解无约束优化问题时具有一定的优越性。
2. 人工蜂群算法和Hooke-Jeeves方法
为了便于描述新算法,首先对人工蜂群算法和改进的Hooke-Jeeves方法进行简要说明。
2.1. 人工蜂群算法
人工蜂群算法用于求解无约束优化问题
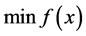 (1)
(1)
其中自变量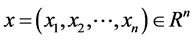 ,n指维数。目标函数
,n指维数。目标函数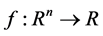 。具体步骤如下:
。具体步骤如下:
步骤一:初始化。
初始化种群大小NP,食物源数目 ,采蜜蜂数目NS。接着随机产生NS个n维实向量(n指优化问题的维数),令
,采蜜蜂数目NS。接着随机产生NS个n维实向量(n指优化问题的维数),令 表示产生的第i个向量,每维分量的生成公式如下:
表示产生的第i个向量,每维分量的生成公式如下:
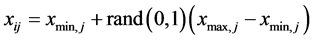 (2)
(2)
式中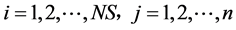 ,
,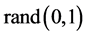 是
是 之间服从均匀分布的随机数,
之间服从均匀分布的随机数,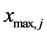 和
和 表示第j维的上下界。
表示第j维的上下界。
将这些向量随机分配给NS只采蜜蜂,用公式(3)计算每只采蜜蜂对应食物源的适应度值,同时用变量Xbest记录适应度值最大的食物源。
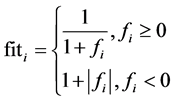 (3)
(3)
步骤二:重复地对食物源进行更新,直到终止条件满足。
① 采蜜蜂阶段
基于旧的食物源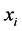 产生一个候选解
产生一个候选解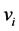 ,公式如下:
,公式如下:
 (4)
(4)
式中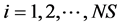 ;k是从集合
;k是从集合 中随机选择的一个整数,并且k必须不同于i;j是从集合
中随机选择的一个整数,并且k必须不同于i;j是从集合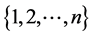 中随机选择的一个整数;
中随机选择的一个整数;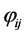 是服从[−1,1]之间均匀分布的随机数。
是服从[−1,1]之间均匀分布的随机数。
计算并比较候选解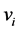 和食物源
和食物源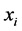 两者的适应度值,用贪婪算子在
两者的适应度值,用贪婪算子在 和
和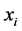 间做选择:如果
间做选择:如果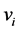 的适应度值不小于
的适应度值不小于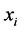 的适应度值,那么用
的适应度值,那么用 替代
替代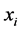 ;否则
;否则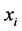 保留。
保留。
② 跟随蜂阶段
跟随蜂根据每个食物源 的被选择概率
的被选择概率 ,利用轮盘赌算子决定
,利用轮盘赌算子决定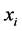 是否被选择进行更新,即只有当随机数
是否被选择进行更新,即只有当随机数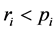 时,才用公式(4)产生
时,才用公式(4)产生 的一个候选食物源
的一个候选食物源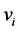 ,计算并比较候选解和旧食物源的适应度值,用贪婪算子在两者之间做取舍。其中每个食物源的被选择概率
,计算并比较候选解和旧食物源的适应度值,用贪婪算子在两者之间做取舍。其中每个食物源的被选择概率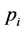 的公式如下:
的公式如下:
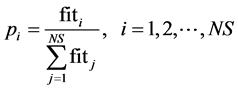 (5)
(5)
③ 侦查蜂阶段
如果有食物源 在Limit循环次数之内一直没有被更新,那么
在Limit循环次数之内一直没有被更新,那么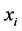 就会被抛弃,用公式(2)产生一个新的食物源来代替
就会被抛弃,用公式(2)产生一个新的食物源来代替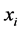 。Limit是预先给定的一个值。
。Limit是预先给定的一个值。
④ 更新gbest
找出当前种群中的最大适应度值,与原来的Fitbest比较,适应度值更高的作为新的Fitbest,同时将Fitbest对应的食物源存入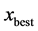 中。
中。
步骤三:输出最终的 作为优化问题的近似解。
作为优化问题的近似解。
2.2. Hooke-Jeeves方法
Hooke-Jeeves方法包含两种类型的移动:探测移动(exploratory move)和模式移动(pattern move)。在确定了一个初始基点之后,探测移动依次沿n个坐标轴进行,用以确定新的基点和有利于函数数值下降的方向;模式移动沿相邻两个基点连线方向进行,试图顺着“山谷”使函数值更快地减小。这两种移动交替地进行直到终止条件满足,如图1所示,带箭头的实线为探测移动,不带箭头的实线为模式移动。
探测移动的主要步骤描述在算法1中(见图2)。假定x0是基点,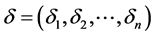 是n个方向上各自的步长,
是n个方向上各自的步长,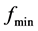 是当前目标函数的最小值。x1是过渡向量,用于存储探测移动后得到的点。如果探测移动成功,即两个解x0和x1满足关系
是当前目标函数的最小值。x1是过渡向量,用于存储探测移动后得到的点。如果探测移动成功,即两个解x0和x1满足关系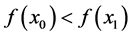 ,那么从x0处以
,那么从x0处以 为方向进行模式移动,模式移动后得到的点记为
为方向进行模式移动,模式移动后得到的点记为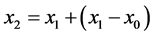 。Hooke-Jeeves方法的主要步骤见算法2 (图3)。算法2中引入了辅助步长
。Hooke-Jeeves方法的主要步骤见算法2 (图3)。算法2中引入了辅助步长 用于终止算法;步长缩减率
用于终止算法;步长缩减率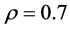 。
。
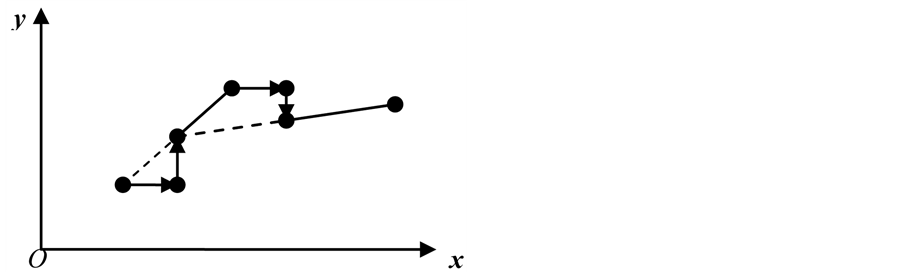
Figure 1. An example of Hooke-Jeeves method
图1. Hooke-Jeeves方法的一个例子

Figure 2. The main steps of exploratory move
图2. 探测移动主要步骤

Figure 3. The main steps of Hooke-Jeeves Method
图3. Hooke-Jeeves方法主要步骤
3. 基于Hooke-Jeeves的改进人工蜂群算法
为了加快基于Hooke-Jeeves的人工蜂群算法HABC [8] 的收敛速度,并且防止算法陷入局部最优,我们提出基于Hooke-Jeeves的改进人工蜂群算法。本节首先描述三个改进策略,随后对新算法进行具体说明。
3.1. 采蜜蜂更新公式
在采蜜蜂阶段,根据文献 [9] 将候选解的产生公式改为
 (6)
(6)
式中,指标r1和r2是从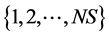 里随机选的两个不同的整数,且均不同于i;
里随机选的两个不同的整数,且均不同于i; 是当前种群中最好的个体(指目标函数最小的个体);j是从
是当前种群中最好的个体(指目标函数最小的个体);j是从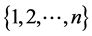 里随机取的一个整数;
里随机取的一个整数;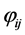 是[−1,1]之间服从均匀分布的随机数。原始的候选解公式(4)精于全局搜索、疏于局部寻优,导致算法的收敛速度减慢。而公式(6)是在前一次迭代后得到的最好个体附近产生候选解,这样充分利用了最好个体的信息,并且大大增加了算法的局部寻优能力,从而提升了收敛速度。
是[−1,1]之间服从均匀分布的随机数。原始的候选解公式(4)精于全局搜索、疏于局部寻优,导致算法的收敛速度减慢。而公式(6)是在前一次迭代后得到的最好个体附近产生候选解,这样充分利用了最好个体的信息,并且大大增加了算法的局部寻优能力,从而提升了收敛速度。
另外蜂群个体的适应度值计算公式如下:
 (7)
(7)
式中, 是指函数值按从大到小排序后第i个解在整个种群中的顺序号;SP是选择压力,取值为[1.0, 2.0],实验中取了中间值1.5;NS是食物源数目。
是指函数值按从大到小排序后第i个解在整个种群中的顺序号;SP是选择压力,取值为[1.0, 2.0],实验中取了中间值1.5;NS是食物源数目。
3.2. 跟随蜂更新公式
在跟随蜂阶段,根据文献 [10] 将候选解的产生公式改为
 (8)
(8)
式中,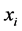 是第i个食物源;
是第i个食物源;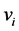 是第i个食物源的候选解,d是从
是第i个食物源的候选解,d是从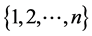 里依次取的整数;
里依次取的整数; 是当前种群中的最好个体,
是当前种群中的最好个体,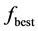 是将
是将 带入公式(3)得到的值;
带入公式(3)得到的值; 是[−1,1]之间服从均匀分布的随机数;j是从
是[−1,1]之间服从均匀分布的随机数;j是从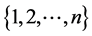 里随机取的一个整数。公式(8)将
里随机取的一个整数。公式(8)将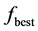 作为候选解产生公式的误差校正项乘子,根据参考文献 [10] 所述,此举能够加快算法的收敛速度。
作为候选解产生公式的误差校正项乘子,根据参考文献 [10] 所述,此举能够加快算法的收敛速度。
3.3. 局部寻优初始基点的选择
在Hooke-Jeeves方法中,每Nc次循环后以最好个体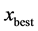 为基点进行一次Hooke-Jeeves搜索,如果此时
为基点进行一次Hooke-Jeeves搜索,如果此时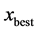 为靠近局部最优解的点,那算法很容易就陷入了局部最优。PABC [6] 算法是采用从任意解往最好解方向移动后的新个体上进行搜索,虽然能一定程度上避免陷入局部最优,但是对于任取的个体,即使往最好个体方向上移动之后仍无法确定会不会很偏离最优值。
为靠近局部最优解的点,那算法很容易就陷入了局部最优。PABC [6] 算法是采用从任意解往最好解方向移动后的新个体上进行搜索,虽然能一定程度上避免陷入局部最优,但是对于任取的个体,即使往最好个体方向上移动之后仍无法确定会不会很偏离最优值。
本文对Hooke-Jeeves方法进行的局部搜索做了改动,一个很自然的想法就是折中处理,即取目标函数值处于中间的个体,再往最好个体方向稍做移动得到新的个体U,以U为基点进行Hooke-Jeeves搜索。U的生成公式如下:
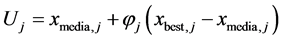 (9)
(9)
式中, ;
;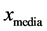 表示目标函数值位于中间的个体;
表示目标函数值位于中间的个体; 表示目标函数值最小的个体;
表示目标函数值最小的个体;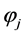 是[0,1]之间服从均匀分布的随机数。本文还将探测移动的步长公式更改为:
是[0,1]之间服从均匀分布的随机数。本文还将探测移动的步长公式更改为:
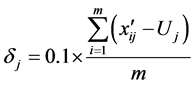 (10)
(10)
式中,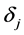 指第
指第 维的探测移动步长值;
维的探测移动步长值;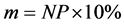 是用于计算步长的个体数;
是用于计算步长的个体数;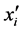 是按目标函数值从大到小排序后序号为i的个体;
是按目标函数值从大到小排序后序号为i的个体; 是用公式(9)得到的新个体。该步长公式取的是前m个最好解与新解U之间的平均距离,也就是以U为基点,朝着前m个最好解的方向进行搜索。迭代初期,由于种群的多样性,
是用公式(9)得到的新个体。该步长公式取的是前m个最好解与新解U之间的平均距离,也就是以U为基点,朝着前m个最好解的方向进行搜索。迭代初期,由于种群的多样性,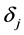 会偏大;随着种群渐渐收敛,种群间的差距会渐渐缩小,从而步长也会随之减小。
会偏大;随着种群渐渐收敛,种群间的差距会渐渐缩小,从而步长也会随之减小。
U与 的选取使得Hooke-Jeeves搜索在一个相对不错的个体上沿着指向最好解的方向进行,既避免了在较差解上Hooke-Jeeves搜索的浪费,又避免了在最好解上Hooke-Jeeves搜索的停滞。Hooke-Jeeves搜索方法的终止参数是
的选取使得Hooke-Jeeves搜索在一个相对不错的个体上沿着指向最好解的方向进行,既避免了在较差解上Hooke-Jeeves搜索的浪费,又避免了在最好解上Hooke-Jeeves搜索的停滞。Hooke-Jeeves搜索方法的终止参数是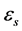 ,当辅助步长
,当辅助步长 时,算法会自动跳出局部搜索循环。选取Hooke-Jeeves搜索得到的个体与
时,算法会自动跳出局部搜索循环。选取Hooke-Jeeves搜索得到的个体与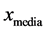 中函数值较小的那个个体,从整体上把握种群的发展方向。
中函数值较小的那个个体,从整体上把握种群的发展方向。
3.4. 改进算法
我们提出的新算法称为基于Hooke-Jeeves的改进人工蜂群算法,简记为IHABC。算法的大体框架同HABC一致,主要有两个阶段:
第一阶段是全局搜索阶段,用人工蜂群算法ABC搜索较优质的解,采蜜蜂阶段改用公式(6),跟随蜂阶段改用公式(8),其它地方与ABC算法相同。
第二阶段是局部寻优阶段,每NC次循环调用一次Hooke-Jeeves方法对公式(9)得到的新解U进行局部寻优,对应的步长用公式(10)计算。接着进行如1.2节所述的两种移动:探测移动和模式移动,探测移动一次只考虑一个分量用以确定合适的寻优方向,而下一步的模式移动是为了在探测移动得到的方向上进行加速寻优。这两种移动交替进行不断重复直到开采阶段的终止条件满足,得到的结果记为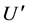 。比较
。比较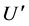 与
与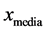 两者的目标函数值,目标函数值更小者替代原来的
两者的目标函数值,目标函数值更小者替代原来的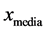 。
。
搜索阶段和开采阶段重复进行直到终止条件满足,终止条件可以是最大函数计算次数、最大循环次数或者与理论最优值之间的差异很小等。为了表述更清晰,图4给出了IHABC算法(算法3)的整个过程。
4. 数值实验
本实验是在Windows XP系统,Intel Core13(2.4GHz CPU/2G)的环境下运行的,使用Matlab 2012b软件编写的程序。本节将ABC算法、HABC算法以及IHABC算法在30个基准函数 [11] 上做了测试,比较了三个算法独立运行50次得到的基准函数最小值的平均值和标准差。

Figure 4. The main steps of IHABC
图4. IHABC主要步骤
4.1. 基准函数和参数设置
基准函数是从检验全局优化算法表现的函数库中选出的有代表性的函数,涵盖了不同的维数、不同的特点(单峰U/多峰M、可分S/不可分N),基本信息见表1,具体的表达式详见参考文献 [7] 和 [11] 。由于多峰函数和不可分函数能较好地检测智能优化算法的优劣,我们选择了16个多峰不可分函数,10个单峰不可分函数,1个多峰可分函数,2个单峰可分函数。
为了便于比较,三个算法中ABC阶段的参数设置均取相同的值:种群数NP = 50;食物源数目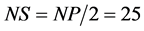 ;limit = NS × n,n指优化问题的维数;最大函数计算次数300000。HABC中参数设置见文献 [8] ,IHABC中其它参数设置如下:
;limit = NS × n,n指优化问题的维数;最大函数计算次数300000。HABC中参数设置见文献 [8] ,IHABC中其它参数设置如下: ,
,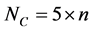 ,
, ,
,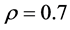 ,
,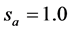 ,
,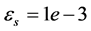 。
。
4.2. 实验结果
每个算法在基准函数C01-C30上独立运行50次得到函数最小值的平均值和标准差总结在表2中,较好的实验结果用黑色粗体标出。
在单峰可分Sphere (SP)函数C27上,新算法IHABC算法在50次实验中均取得了全局最小值0,标准差也为零,求解精度和算法的稳定性都超过了ABC和HABC算法;在单峰可分离Quartic (QU)函数
Table 1. The information of benchmark functions
表1. 函数基本信息
Table 2. The results of ABC, HABC and IHABC on function C01-C30
表2. ABC、HABC和IHABC算法在函数C01-C30上的结果
C20上,ABC和HABC的性能相当,其平均最优值为0.0370203和0.0351516,标准差为0.00797128和0.00822433,而IHABC的平均最优值为1.76447e−05,标准差为1.42544e−05,比ABC和HABC算法提高了3个数量级。多峰可分Michalewicz (MI)函数C17,取参数m = 10和维数n = 5时,它有5!个局部最优点,三种算法的平均最优值均达到全局最小值−4.68766,HABC和ABC算法的标准差均为2.75367e−15,IHABC的标准差为2.54399e−15,IHABC算法标准差最小。
对于单峰不可分Beale (BE)函数C01、Matyas (MA)函数C03、Colville (CO)函数C08、Rosenbrock (RO)函数C25、Schwefel’s Ridge (SR)函数C26、Schwefel’s problem 2.22 (S22)函数C28和Zakharov (ZA)函数C29,均无局部最小值,只有一个全局最小值,IHABC算法在50次试验中均找到了全局最小值0,标准差是0,寻优性能高于ABC和HABC算法。其中Colville函数在唯一最小值点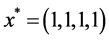 附近有一个鞍点,所以HABC算法的平均最优值为1.4811e−06,而ABC算法在50次试验中未能找到全局最小值,其平均最优函数值为0.169416,最好的一次寻优结果为
附近有一个鞍点,所以HABC算法的平均最优值为1.4811e−06,而ABC算法在50次试验中未能找到全局最小值,其平均最优函数值为0.169416,最好的一次寻优结果为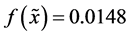 ,其中
,其中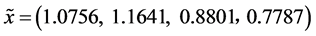 ;Rosenbrock函数是单模态的高维函数,变量间相互关联,其内部是一个长而狭窄,形如抛物线的平坦山谷地带,最小值点
;Rosenbrock函数是单模态的高维函数,变量间相互关联,其内部是一个长而狭窄,形如抛物线的平坦山谷地带,最小值点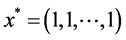 位于其中,ABC算法很难收敛于全局最优值
位于其中,ABC算法很难收敛于全局最优值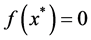 ,ABC和HABC算法的50次实验的平均最优值分别为0.213231和5.04318e−06,ABC算法的求解精度比IHABC算法低。
,ABC和HABC算法的50次实验的平均最优值分别为0.213231和5.04318e−06,ABC算法的求解精度比IHABC算法低。
对于单峰不可分函数Helical valley problem (HV) C07、Powell (PO)函数C19和Schwefel’s Problem 2.21 (S21)函数C21,多峰不可分函数Perm (PE) C09和Power Sum (PS) C10,IHABC算法的寻优精度和稳定性要优于HABC和ABC算法,HABC算法则优于ABC算法。
对于多峰不可分函数Shekel’s Foxholes (SF)函数C04、Shubert (SH)函数C05、Hartman 3 (H3,4)函数C06,Shekel’s Problem Family (S4,10)函数C11和Hartman 6 (H6,4)函数C15,三种算法的平均最优值均能达到全局最小值,分别为0.998004、−186.731、−3.86278、−10.5364和−3.322;Goldstein and Price (GP)函数C02、Fletcher-Powell (FP)函数C12和Griewank (GR)函数C24,IHABC算法和HABC算法性能相当,平均最优值都取到了全局最小值,寻优性能和稳定性都超过了ABC算法;对于Weierstrass (WE)函数C22、Ackley (AC)函数C23 (n = 30维)和Ackley (AC)函数C30 (n = 100维),HABC算法和ABC算法性能相当,IHABC算法优于IHABC和ABC,能够得到全局最小值0,标准差也为0,对于Ackley函数,30维和100维时IHABC算法的寻优结果一样,表明了该算法的稳健性。
对于多峰不可分函数Whitley (WI) C18,维数n = 10时,全局最小值点为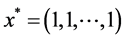 ,全局最小值为
,全局最小值为 ,ABC算法在50次实验中均找不到全局最小值;IHABC算法有43次找到全局最小值0,有7次找到局部最小值0.9865;HABC算法有47次找到全局最小值0,有2次寻优得到0.9865,还有1次找到的最优值为6.6613e−16,HABC在函数C18上寻优精度最高。
,ABC算法在50次实验中均找不到全局最小值;IHABC算法有43次找到全局最小值0,有7次找到局部最小值0.9865;HABC算法有47次找到全局最小值0,有2次寻优得到0.9865,还有1次找到的最优值为6.6613e−16,HABC在函数C18上寻优精度最高。
Modified Langerman函数C13,C14,C16是非对称的复杂多模态函数,其局部最优解个数未知且随机分布,随着维数的增加,搜索难度增大。当维数n = 2时,三种算法在50次实验中均取得了全局最小值−1.08094,IHABC算法的标准差最小,算法最稳定;当维数n = 5时,50次实验中ABC、HABC、IHABC算法的平均最优值分别为−0.964959,−0.963356和−0.954508,标准差分别为0.000142,0.008745和0.016397,50次实验中三种算法分别42次、48次和33次得到全局最小值−0.965,IHABC算法10次得到局部最小值−0.9398,ABC算法在n = 5时,性能最好;当维数n = 10时,ABC、HABC、IHABC算法的平均最优值分别为−0.533924、−0.569837和−0.6077,标准差分别为0.084979、0.143236和0.221634,50次实验中,ABC、HABC和IHABC算法分别有0、3和4次达到全局最小值−0.9605,分别有47、43和24次寻优得到局部最小值−0.5132,意味着该函数在多个点处取得局部极小值−0.5132,ABC算法另外三次的寻优结果为−0.8057,−0.8059和−0.9649,HABC算法还得到局部最优值−0.9080三次,−0.8060一次,IHABC算法得到局部最优值−0.2749四次,−0.4286三次,−0.4829和−0.9645各两次,−0.5164、−0.5168、−0.5170、−0.8019、−0.80306、−0.9585、−0.9614、−0.9637、−0.9640、−0.9641和−0.9644各一次。与ABC、HABC算法相比,IHABC算法的通用性和局部寻优能力更强,在得到全局最小值的同时,能搜索到更多的局部最优值。
总体来说,新算法IHABC的性能在23个函数上优于HABC算法,在5个函数上与HABC相当,在2个函数上略逊于HABC算法。实验结果证明了IHABC算法比HABC以及ABC算法在寻优精度上有了相当程度的提高。
5. 结论
基于Hooke-Jeeves的人工蜂群算法HABC,其全局搜索能力与局部寻优能力不均衡,局部寻优阶段初始解的选择易导致算法陷入局部最优,为解决这些问题本文提出基于Hooke-Jeeves的改进人工蜂群算法IHABC。新算法通过三个改进策略分别对蜂群的采蜜蜂更新公式、跟随蜂更新公式和局部寻优阶段的初始基点的选择以及局部寻优的步长进行了调整,最后将算法在30个测试函数上进行了数值实验。实验结果表明,新算法与HABC和ABC算法相比,在大部分测试函数上得到的全局最优解的精度更高,算法更稳定。
基金项目
教育部人文社会科学青年基金项目(12YJCZH179),江苏省大规模复杂系统数值模拟重点实验室开放基金项目(201601)。
文章引用
孙越泓,丁亚英. 基于Hooke-Jeeves的改进人工蜂群算法
An Improved Artificial Bee Colony Algorithm Based on Hooke-Jeeves Method[J]. 计算机科学与应用, 2017, 07(02): 134-145. http://dx.doi.org/10.12677/CSA.2017.72017
参考文献 (References)
- 1. Karaboga, D. and Basturk, B. (2008) On the Performance of Artificial Bee Colony (ABC) Algorithm. Applied Soft Computing, 8, 687-697. https://doi.org/10.1016/j.asoc.2007.05.007
- 2. Karaboga, D. and Akay, B. (2009) A Comparative Study of Artificial Bee Colony Algorithm. Applied Mathematics and Computation, 214, 108-132. https://doi.org/10.1016/j.amc.2009.03.090
- 3. Zhu, G.P. and Kwong, S. (2010) Gbest-Guided Artificial Bee Colony Algorithm for Numerical Function Optimization. Applied Mathematics and Computation, 217, 3166-3173. https://doi.org/10.1016/j.amc.2010.08.049
- 4. Urselmann, M., Barkmann, S., Sand, G., et al. (2011) A Memetic Algorithm for Global Optimization in Chemical Process Synthesis Problems. IEEE Transactions on Evolutionary Computation, 15, 659-683. https://doi.org/10.1109/TEVC.2011.2150753
- 5. Bansal, J.C., Sharma, H., Aryak, V., et al. (2013) Memetic Search in Artificial Bee Colony Algorithm. Soft Computing, 17, 1911-1928. https://doi.org/10.1007/s00500-013-1032-8
- 6. Gao, W.F., Liu, S.Y. and Huangl, L. (2013) A Novel Artificial Bee Colony Algorithm with Powell’s Method. Applied Soft Computing, 13, 3763-3775. https://doi.org/10.1016/j.asoc.2013.05.012
- 7. Kang, F., Li, J. and Ma, Z. (2011) Rosenbrock Artificial Bee Colony Algorithm for Accurate Global Optimization of Numerical Functions. Information Science, 181, 3508-3531. https://doi.org/10.1016/j.ins.2011.04.024
- 8. Kang, F., Li, J. and Li, H. (2013) Artificial Bee Colony Algorithm and Pattern Search Hybridized for Global Optimization. Applied Soft Computing, 13, 1781-1791. https://doi.org/10.1016/j.asoc.2012.12.025
- 9. Gao, W.F. and Liu, A.Y. (2012) A Modified Artificial Bee Colony Algorithm. Computers & Operations Research, 39, 687-697. https://doi.org/10.1016/j.cor.2011.06.007
- 10. Banharnsakun, A. and Achalakul, T. (2011) The Best-So-Far Selection in Artificial Bee Colony Algorithm. Applied Soft Computing, 11, 2888-2901. https://doi.org/10.1016/j.asoc.2010.11.025
- 11. Chelouah, R. and Siarry, P. (2000) A Continuous Genetic Algorithm Designed for the Global Optimization of Multimodal Functions. Journal of Heuristics, 6, 191-213. https://doi.org/10.1023/A:1009626110229
