Hans Journal of Data Mining
Vol.
12
No.
02
(
2022
), Article ID:
50032
,
10
pages
10.12677/HJDM.2022.122014
基于核相似性的模糊多核最小二乘支持向量机
宋菲菲1,2,何强1,2*,王恒友1,2,张长伦1,2,陈琳琳1,2
1北京建筑大学理学院,北京
2北京建筑大学大数据建模理论与技术研究所,北京
收稿日期:2022年3月2日;录用日期:2022年3月31日;发布日期:2022年4月8日

摘要
最小二乘支持向量机(Least Squares Support Vector Machine, LSSVM)由于同等对待所有样例,从而易受噪声干扰,影响分类性能。模糊LSSVM的提出一定程度上克服了以上问题。本文给出了一种新的样例隶属度计算方法,其在特征空间中,利用每一样例与其他样例核相似性获得隶属度,并将其应用于模糊多核LSSVM (Fuzzy Multi-Kernel LSSVM, FMK-LSSVM),得到具有强鲁棒性的基于核相似性的模糊多核LSSVM。实验结果验证该方法的可行性与有效性。
关键词
最小二乘支持向量机,隶属度,多核学习,核相似性

Kernel Similarity-Based Fuzzy Multi-Kernel Least Squares Support Vector Machine
Feifei Song1,2, Qiang He1,2*, Hengyou Wang1,2, Changlun Zhang1,2, Linlin Chen1,2
1School of Science, Beijing University of Civil Engineering and Architecture, Beijing
2Institute of Big Data Modelling and Technology, Beijing University of Civil Engineering and Architecture, Beijing
Received: Mar. 2nd, 2022; accepted: Mar. 31st, 2022; published: Apr. 8th, 2022

ABSTRACT
Least squares support vector machine (LSSVM) is vulnerable to noise and affects the classification performance because it treats all samples equally. Fuzzy LSSVM overcomes the above problems by introducing membership. In this paper, we develop a new method to compute membership. In the feature space, the membership degree is obtained by using the kernel similarity between each sample and other samples, and applied to fuzzy multi-kernel LSSVM (FMK-LSSVM) to obtain a strong robust FMK-LSSVM. Experimental results verify the feasibility and effectiveness of this method.
Keywords:LSSVM, Membership, Multi-Kernel Learning, Kernel Similarity

Copyright © 2022 by author(s) and Hans Publishers Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY 4.0).
http://creativecommons.org/licenses/by/4.0/


1. 引言
支持向量机(Support Vector Machine, SVM)以统计学理论为基础 [1] [2],是一种性能良好的机器学习方法,有效地解决了局部极小值点、小样本、非线性等实际问题,目前已成功应用于模式识别、回归预测、聚类问题等诸多领域,有力地推动了机器学习理论与应用的发展。但是SVM由于需要求解二次优化问题,使其具有高时间复杂度。1999年Suykens等提出最小二乘支持向量机(LSSVM) [3],通过求解线性方程组来得到决策模型,大大降低了算法计算量。LSSVM利用核技巧解决非线性可分性问题,但同时也带来了核选择难题,为解决这一问题,各类多核学习方法被引入LSSVM,即多核组合代替单核 [4] [5] [6] [7],即多核LSSVM (Multi-Kernel LSSVM, MK-LSSVM) [8]。
由于同等对待每一样例,包括LSSVM在内的各类SVM算法都易受噪音数据影响。模糊隶属度的引入,得到模糊SVM (Fuzzy SVM, FSVM) [9],一定程度上缓解了这一问题。当然这一思想同样适用于LSSVM,从而有了模糊LSSVM (Fuzzy LSSVM, F-LSSVM) [10]。对于FSVM与F-LSSVM来说,求得样例隶属度都是至关重要的。现有各类隶属度计算方法,都是基于对噪音的检测。一般而言,噪音应该被赋予较小的隶属度,从而降低其对最终决策函数的影响。有基于Kohonen自组织映射、模糊性指数和模糊c-maan算法等技术的隶属度计算方法 [9]。也有学者将隶属度设置为点与其类中心之间距离的函数 [11] [12] [13]。此外,通过考虑样例的属性和决策之间的不一致性,He等提出了一类基于模糊粗糙集的隶属度计算方法 [14]。上述隶属度的引入,一定程度上提高了SVM的鲁棒性。但所有隶属度计算方法都未结合SVM算法本身特点,只是在样例所在原始空间中度量其相似性程度,从而计算隶属度。然而SVM是在特征空间中实现对样例的分割。原始空间与特征空间的不一致可能造成传统隶属度并不能很好反映样例在特征空间中的重要性程度。本文中,针对MK-LSSVM,通过其组合核获得特征空间中的样例相似性,给出一种基于样本核相似性的隶属度计算方法。从而得到了基于核相似性的模糊MK-LSSVM (Kernel Similarity-Based FMK-LSSVM, KS-FMKLSSVM)。
本文后续内容安排如下,第2节介绍LSSVM、MK-LSSVM和FMK-LSSVM的相关知识;基于核相似性的隶属度计算方法和KS-FMKLSSVM算法在第3节中详细说明;第4节给出实验结果,第5节为结论。
2. 相关知识
2.1. 最小二乘支持向量机(LSSVM)
与经典SVM相同,LSSVM模型通过最优超平面解决分类问题,其主要思想是通过核函数实现在高维特征空间中对样例的线性分割。特征空间中的最优分割超平面对应于原始空间中的非线性分割函数。
设有训练集 ,其中 。 为某非线性映射,将样本由原空间映入高维特征空间,SVM在特征空间中构造最优分割超平面 [1]。设 与b为特征空间中分割超平面的法向量与偏置。超平面为 。LSSVM需要求解以下二次规划问题:
(1)
其中C为惩罚系数、 为松弛变量。引入拉格朗日乘子,可得对偶问题 [3]:
(2)
式中: , 是所有元素为1的列向量,I是N阶单位矩阵,其中 , 为核函数 [2]。通过求解上述方程组得到LSSVM决策函数:
(3)
2.2. 多核LSSVM
核函数度量了样本在特征空间中的相似性,但是单个核对样本相似性的刻画能力往往有限,核函数与核参数的选择对LSSVM性能有关键影响。然而,当前并不存核函数选择的通用方法,大多靠经验或试算,效果往往不理想且效率低下。作为核方法的重要成果,多核学习近年来已成为机器学习领域广大学者的研究热点 [4] [5] [6] [7]。多核的意义主要体现在通过多个核函数组合可以更准确地表达数据间的相似性,同时也克服了核函数选择这一难题。多核学习成果的引入将使我们可以通过使用多个核函数,而不是一个核函数来表达样本间的相似性,即通过多个核函数的融合来得到样本间最终的相似性 [15]。将多核学习引入到LSSVM,即得到多核LSSVM (MK-LSSVM)。有效避免了核函数及其参数选择难题。线性加权组合是最常用的多核组合方式:
(4)
其中, 分别是基础核与核权重,本文采用该种加权求和的组合方式。在LSSVM模型中,用多核替代单核,得到MK-LSSVM决策函数为:
(5)
MK-LSSVM性能很大程度上依赖于组合核,而其关键就是核权重。本文中,利用核对齐方法 [16] [17] [18],通过求解以下优化问题来得到核权重 :
(6)
这里K是组合核矩阵, 是两个矩阵间的Frobenius内积,其中
(7)
显然,A越大,则组合核矩阵K与理想核矩阵 间的距离越小,即组合核对数据相似性刻画能力越强 [16]。为方便求解,(6)式可变形为下述优化问题 [17]:
(8)
其中, 是正则项系数。
2.3. 模糊多核LSSVM
LSSVM继承了SVM的优点,实现了结构风险最小化,但也继承了对噪声敏感的缺点。为此,引入隶属度得到模糊LSSVM [10],提升了LSSVM鲁棒性。设 为样本 的隶属度,则训练集可表示为 ,其中 ,模糊多核LSSVM的模型为:
(9)
相应对偶问题为:
(10)
(10)式中, , ,其他符号含义与(2)式相同。通过求解上述方程组得到LSSVM决策函数:
(11)
显然,当 时,FMK-LSSVM模型退化为MK-LSSVM。
3. 基于核相似性的FMK-LSSVM
标准的LSSVM因为平等的对待每个样例,所以易受噪音影响而性能变差。为了缓解这种现象,模糊隶属度被引入,得到模糊LSSVM,使每一训练样例因为重要性不同而对分割超平面产生不同的影响,从而提升算法鲁棒性。模糊隶属度的计算是模糊LSSVM的关键。本节通过数据间的核相似性衡量每个样本的隶属度,为与其核相似性高的样例赋予较高的隶属度,为噪音赋予较低的隶属度,来降低噪音的影响。
SVM中的核函数不仅将原空间中的问题转换为特征空间的问题,还有效衡量了数据间的相似性。此处,使用FMK-LSSVM的组合核来度量样本间相似性,两个样例间的核函数值越大,则表明这两个样例间的相似性越高。对于某一样例,与其相似性大且标签一致的样例越多,则该样例越能代表此类数据的特征,应赋予较大的隶属度,反之亦然。基于上述思想,本节提出了一种基于核相似性的隶属度计算方法。主要过程如下。
首先利用组合核函数计算训练集俩俩样本之间的核函数值,并从大到小排序。通过参数 确定衡量相似性大小的阈值 ,若两样例间核函数值大于 ,则认为其相似性大;从而可以得到每个样例与其相似度大的同类与异类样例数,最终通过S型函数计算得到每个样例的隶属度值 [19]。S型函数表达式为 ,其可使正常样例与噪音的隶属度差异更大,最大程度降低噪音的干扰,其中S型函数中的参数 用来控制这种差异性的程度。本文中,我们取 。隶属度函数可被写为:
(12)
其中 分别是与样例 类别相同且相似性达到阈值 的样例个数, 分别为与样例 类别相同且相似性达到阈值 的核函数值的和,计算公式如下:
(13)
(14)
此外, 。
主要计算过程如算法1所示:
将基于核相似性引入FMK-LSSVM,即得到KS-FMKLSSVM。下节中,将通过实验验证KS-FMKLSSVM的可行性与有效性。
4. 实验
论文中的数据选自UCI中的二分类数据集。本节中将KS-FMKLSSVM与其他3类LSSVM方法进行对比。分别是普通MK-LSSVM、基于模糊粗糙集隶属度的模糊多核LSSVM (Fuzzy Rough Set Based FMK-LSSVM, FR-FMKLSSVM)和基于欧氏距离隶属度 [13] 的模糊多核LSSVM (Euclidean Distance Based FMK-LSSVM, ED-FMKLSSVM)。所选数据集的信息如表1所示。
Table 1. The information of UCI dataset in experiment
表1. 实验中的UCI数据集信息
实验中均是选择70%作为训练集,30%作为测试集,重复10次试验求平均得到最终结果。为检验算法鲁棒性,每次训练集中随机选取20%样例改变其标签,作为噪音放回训练集中。此外,本节中多核算法中组合核都由7个高斯核作为基本核组合而成,核参数分别为 。各个算法测试经度与训练时间结果表2和表3所示。
Table 2. Testing accuracy (%) values of 4 algorithms
表2. 4种方法的测试精度(%)
Table 3. Training time (s) of 4 algorithms
表3. 4种方法的训练时间(s)
实验结果显示,本文提出的KS-FMKLSSVM在UCI的8个数据集上,分类精确都较其他算法有较明显提高,而时间消耗与其他方法相比并没有显著增加,尤其是与其他FMK-LSSVM算法相比,时间支出基本相当。这也验证了本文所提隶属度计算方法的可行性与有效性。
ROC曲线是机器学习常用的模型性能比较指标,曲线横纵坐标分别是假正例率和真正利率。A算法的ROC曲线被B算法的曲线“包住”,则B算法性能优于前者;如果曲线交叉,可以根据ROC曲线下面积大小进行比较,也即AUC值 [20]。图1是部分数据集上4中算法的ROC曲线。从图中我们可以看出,在各个数据集上,KS-FMKLSSVM算法的ROC曲线都“包住”了其他三种算法的曲线,即KS-FMKLSSVM的综合性能是最佳的,进一步验证了本文给出的隶属度计算方法的有效性。
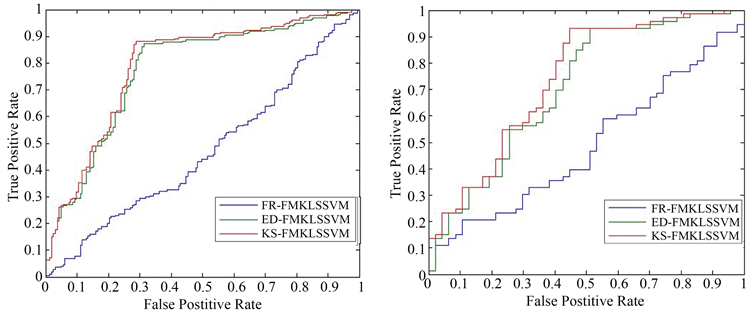
为进一步检验所提KS-FMKLSSVM的鲁棒性,我们以sonar数据为例,展示不同噪声水平下,本文所提方法与其他方法的分类效果的变化情况,结果如图2所示。
从图2可以看出,随着噪音水平的升高,KS-FMKLSSVM的性能在所有四种算法中表现最佳,分类精度最高,且受噪音影响相对较小,这表明了本文提出的隶属度方法可以最大程度提高FMK-LSSVM的鲁棒性。
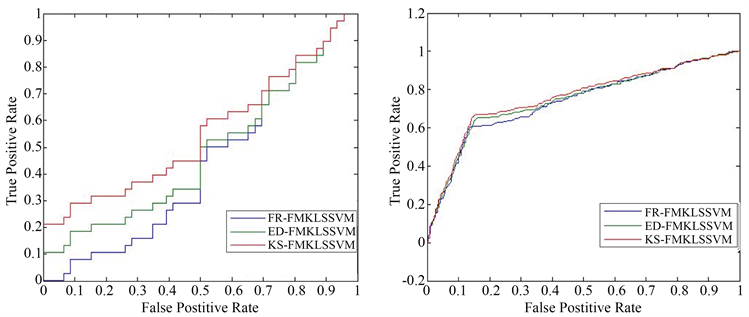 (a) bupa (b) Abalonel
(a) bupa (b) Abalonel
 (c) Winequality(d) Wilt
(c) Winequality(d) Wilt (e) Parkinsons (f) hepatitis
(e) Parkinsons (f) hepatitis
Figure 1. ROC graphs of some data sets
图1. 部分数据集的ROC曲线
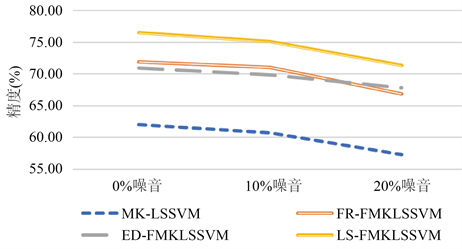
Figure 2. Comparison of robustness of 4 algorithms on sonar
图2. Sonar数据集上4种算法鲁棒性比较
5. 结论
本文针对FMK-LSSVM,提出一种新的隶属度计算方法。该方法以MK-LSSVM中的组合核函数来度量样例间的相似性程度,通过每一样例附近与其相似的同类与异类样例比例的差值来获得该样例的隶属度,并引入到FMK-LSSVM。该隶属度区别于已有的各类隶属度计算方法,其直接以各样例在MK-LSSVM特征空间中的相似性来获得隶属度。LSSVM决策函数同样是在特征空间中构造产生,从而使得该隶属度与LSSVM保持一致性,仿真实验结果也验证了所提方法的有效性。
上述工作虽然取得了一定成果,但仍存在不完善之处,后续相关研究,拟从以下几个方面展开:
1) 模糊隶属度算法中的阈值仍是经验值,后续将进一步研究,设计启发式阈值选取方法,以进一步提高FMK-LSSVM的鲁棒性;
2) 可将线性加权求和的多核模型扩展到局部多核学习模型,使最终的分类器模型进一步利用到样本的信息,提升算法性能。
基金项目
国家自然科学基金(62072024,61473111);北京市教委一般项目(KM202110016001);北京建筑大学科学研究基金(KYJJ2017017,Y19-19,Y18-11,PG2021094);住房和城乡建设部科学技术计划北京建筑大学北京未来城市设计高精尖创新中心开放课题(NO. UDC2019033324,UDC201703332);北京建筑大学课程建设重点培育项目“高等数学ZDXX202008”。
文章引用
宋菲菲,何 强,王恒友,张长伦,陈琳琳. 基于核相似性的模糊多核最小二乘支持向量机
Kernel Similarity-Based Fuzzy Multi-Kernel Least Squares Support Vector Machine[J]. 数据挖掘, 2022, 12(02): 123-132. https://doi.org/10.12677/HJDM.2022.122014
参考文献
- 1. Cortes, C. and Vapnik, V. (1995) Support-Vector Networks. Machine Learning, 20, 273-297. https://doi.org/10.1007/BF00994018
- 2. Vapnik, V. (1998) Statistical Learning Theory. Wiley, New York.
- 3. Suykens, J.A.K. and Vandewalle, J. (1999) Least Squares Support Vector Machine Classifiers. Neural Pro-cessing Letters, 9, 293-300. https://doi.org/10.1023/A:1018628609742
- 4. Zhao, Y.G., Song, Z., Zheng, F. and Shao, L. (2018) Learning a Multiple Kernel Similarity Metric for Kinship Verification. Information Sciences, 430-431, 247-260. https://doi.org/10.1016/j.ins.2017.11.048
- 5. Mehmet, G. and Ethem, A. (2011) Multiple Kernel Learn-ing Algorithms. Journal of Machine Learning Research, 12, 2211-2268.
- 6. Wang, T., Lu, J. and Zhang, G. (2018) Two-Stage Fuzzy Multiple Kernel Learning Based on Hilbert-Schmidt Independence Criterion. IEEE Transactions on Fuzzy Systems, 26, 3703-3714. https://doi.org/10.1109/TFUZZ.2018.2848224
- 7. Wang, Z., Zhu, Z. and Li, D. (2020) Collaborative and Geo-metric Multi-Kernel Learning for Multi-Class Classification. Pattern Recognition, 99, 107050. https://doi.org/10.1016/j.patcog.2019.107050
- 8. Gautam, C. and Tiwari, A. (2018) Localized Multiple Kernel Support Vector Data Description. 2018 IEEE International Conference on Data Mining Workshops (ICDMW), Singa-pore, 17-20 November 2018, 1514-1521. https://doi.org/10.1109/ICDMW.2018.00224
- 9. Lin, C. and Wang, S. (2002) Fuzzy Support Vector Machines. IEEE Transactions on Neural Networks, 13, 464-471. https://doi.org/10.1109/72.991432
- 10. Song, F.F. and He, Q. (2021) Kernel-Target Alignment based Fuzzy Multi-Kernel Least Squares Support Vector Machine. International Journal of Intelligent Information and Management Science, 10, 113-119.
- 11. Huang, H.P. and Liu, Y.H. (2001) Fuzzy Support Vector Machines for Pattern Recognition and Data Mining. International Journal of Fuzzy Systems, 4, 826-835.
- 12. Liu, S.Y. and Du, Z.U. (2007) An Improved Fuzzy Support Vector Machine Method. CAAI Transactions on Intelligent Systems, 2, 30-33.
- 13. 曾山, 同小军, 桑农, 等. 基于对应分析的冗余模糊C均值聚类算法研究. 华中科技大学学报(自然科学版), 2012(40), 107-111.
- 14. He, Q. and Wu, C.X. (2011) Membership Evaluation and Feature Selection for Fuzzy Support Vector Machine Based on Fuzzy Rough Sets. Soft Computing, 15, 1105-1114. https://doi.org/10.1007/s00500-010-0577-z
- 15. De Diego, I.M., Muñoz, A. and Moguerza, J.M. (2010) Methods for the Combination of Kernel Matrices within a Support Vector Framework. Machine Learning, 78, Article No. 137. https://doi.org/10.1007/s10994-009-5135-5
- 16. Wang, T.H., Zhao, D.Y. and Tian, S.F. (2015) An Overview of Kernel Alignment and Its Applications. Artificial Intelligence Review, 43, 179-192. https://doi.org/10.1007/s10462-012-9369-4
- 17. Cortes, C., Mohri, M. and Rostamizadeh, A. (2012) Algorithms for Learning Kernels Based on Centered Alignment. Journal of Machine Learning Research, 13, 795-828.
- 18. Wang, T., Qiu, Y. and Hua, J. (2020) Centered Kernel Alignment Inspired Fuzzy Support Vector Machine. Fuzzy Sets and Sys-tems, 394, 110-123. https://doi.org/10.1016/j.fss.2019.09.017
- 19. He, Q., Zhang, Q.S., Wang, H.Y. and Zhang, C.L. (2020) Local Similarity Based Fuzzy Multiple Kernel One-Class Support Vector Machine. Complexity, 2020, Article ID: 8853277. https://doi.org/10.1155/2020/8853277
- 20. 周志华. 机器学习[M]. 北京: 清华大学出版社, 2016.
NOTES
*通讯作者。
