Statistics and Application
Vol.05 No.01(2016), Article ID:17282,9
pages
10.12677/SA.2016.51005
The Absolute Ruin Risk Model with Constant Interest Investment and a Linear Threshold Dividend Strategy
Ting He, Lijun Wu*
College of Mathematics and System Sciences, Xinjiang University, Urumqi Xinjiang

Received: Mar. 10th, 2016; accepted: Mar. 25th, 2016; published: Mar. 31st, 2016
Copyright © 2016 by authors and Hans Publishers Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/



ABSTRACT
In this paper, the classical absolute ruin risk model and that model with interference are researched based on constant interest investment and a linear threshold barrier dividend strategy. First, renewal equations of moment-generating function and n-th moment with present value of total dividends until absolution ruin are obtained. Second, partial integro-differential equations of Gerber-Shiu function are given.
Keywords:Linear Threshold Dividend, Absolute Ruin Risk Model, Gerber-Shiu Function, Renewal Equation

基于常利率投资和线性阈值分红策略下的绝对破产模型
贺婷,吴黎军*
新疆大学数学与系统科学学院,新疆 乌鲁木齐

收稿日期:2016年3月10日;录用日期:2016年3月25日;发布日期:2016年3月31日

摘 要
在本文中,我们研究基于常利率投资和线性阈值分红策略下的经典的绝对风险破产模型和带干扰的绝对破产风险模型问题。首先,本文得到累计分红现值的矩母函数和累计分红现值的n-阶矩函数的更新方程。然后,著名的Gerber-Shiu期望折现罚金函数所满足的更新方程及边界条件采用类似的方法也可以获得。
关键词 :线性分红阈值,绝对破产,常利率投资,更新方程,Gerber-Shiu期望折现罚金函数

1. 引言
在复合Poisson风险模型 [1] 中,保险公司的盈余过程通常被刻画为
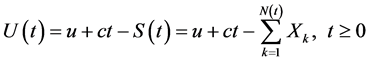 (1)
(1)
盈余模型(2.1)就是著名的经典风险模型。
保险公司在实际经营过程中,除了索赔的不确定因素外,公司自身经营状况、市场的通货膨胀等随机因素也会对保险公司的资产运作产生重要的影响。为了体现这种不确定性,Gerber (1970) [2] 通过引入布朗运动表示公司不确定性的支出或收入,建立了如下带扰动的风险模型:
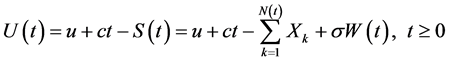 (2)
(2)
其中,(1)和(2)中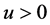 是保险公司初始盈余;
是保险公司初始盈余;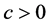 是保费收入率;
是保费收入率; 是服从参数为
是服从参数为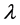 的Poission过程,表示直到
的Poission过程,表示直到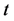 时刻为止的索赔次数;
时刻为止的索赔次数; 为独立同分布随机变量序列,表示索赔额;(2)中
为独立同分布随机变量序列,表示索赔额;(2)中 是常数,表示扰动强度;
是常数,表示扰动强度;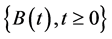 是标准布朗运动。假设
是标准布朗运动。假设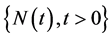 ,
,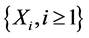 和
和 是相互独立的。
是相互独立的。
在本文中,我们假设当保险公司盈余低于0时,保险公司可以以利率 进行贷款,其贷款量恰好等于当时的赤字,这样就使得盈余水平恢复到0水平,公司可以跟以前一样继续进行经营下去,同时公司会从其保费收入中拿出部分收入来连续偿还贷款 [3] 。对于投资利率 [4] [5] 和红利策略 [6] ,我们假设红利支付方式采取线性阈值分红策略 [7] ,当公司盈余处在0到
进行贷款,其贷款量恰好等于当时的赤字,这样就使得盈余水平恢复到0水平,公司可以跟以前一样继续进行经营下去,同时公司会从其保费收入中拿出部分收入来连续偿还贷款 [3] 。对于投资利率 [4] [5] 和红利策略 [6] ,我们假设红利支付方式采取线性阈值分红策略 [7] ,当公司盈余处在0到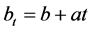 之间 [8] [9] 时,
之间 [8] [9] 时,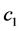 为单位时间公司收取的保费,a
为单位时间公司收取的保费,a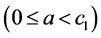 为红利率,盈余会收到投资利率为
为红利率,盈余会收到投资利率为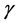 的投资收入,此时只涉及到投资收入,不涉及红利支付。当公司盈余超过
的投资收入,此时只涉及到投资收入,不涉及红利支付。当公司盈余超过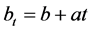 时,红利以a分发,发完红利之后的净保费率以
时,红利以a分发,发完红利之后的净保费率以 表示,盈余会收到投资利率为
表示,盈余会收到投资利率为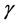 的投资收入。
的投资收入。
将上述假设引入到模型(1)和(2)中,新的盈余过程分别定义为:
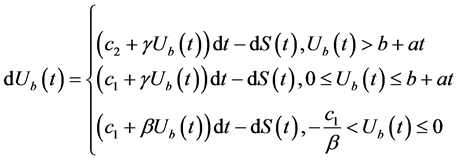 (3)
(3)
和
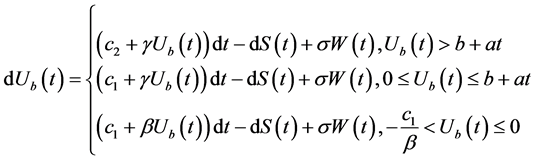 (4)
(4)
其中,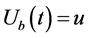 是初始资本。
是初始资本。
定义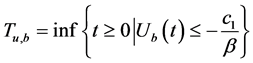 为绝对破产时刻,且对任意
为绝对破产时刻,且对任意 ,均有
,均有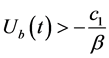 ,则
,则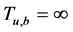 。令
。令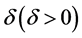 表示折现利息力,
表示折现利息力,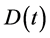 为
为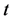 时刻之前的累积红利支付额,则绝对破产时刻前所有红利支付的精算现值定义为
时刻之前的累积红利支付额,则绝对破产时刻前所有红利支付的精算现值定义为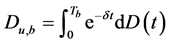 ;
;
红利支付的矩母函数为 ;
;
红利支付的n-阶矩函数为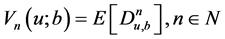 。
。
Gerber-Shiu期望折现罚金函数为
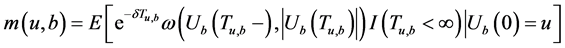
其中, 是示性函数,
是示性函数, 为绝对破产前瞬时盈余;
为绝对破产前瞬时盈余; 为绝对破产赤字,罚金函数
为绝对破产赤字,罚金函数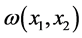 是定义在
是定义在 上的任意非负可测函数。
上的任意非负可测函数。
贯穿于本章,我们假设函数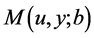 ,
,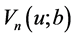 和
和 在各自的定义域上关于
在各自的定义域上关于 和
和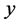 是足够光滑的。
是足够光滑的。
2.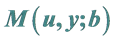 和
和 所满足的积分–微分方程
所满足的积分–微分方程
由初始资本的取值不同,矩母函数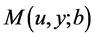 记为
记为
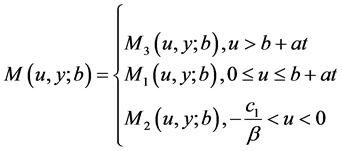
针对模型(4)带常利率投资和线性阈值分红策略下带扰动的绝对破产模型
定理2.1. 当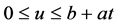 时有
时有
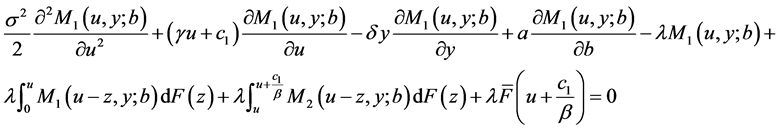 (5)
(5)
当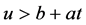 时有
时有
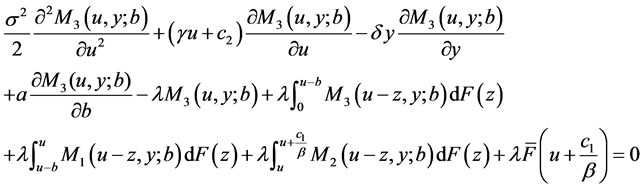 (6)
(6)
当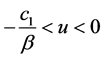 时有
时有
 (7)
(7)
其中边界条件为
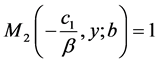 (8)
(8)
 (9)
(9)
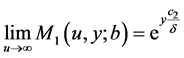 (10)
(10)
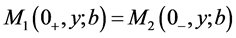 (11)
(11)
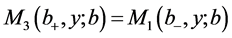 (12)
(12)
证明:为方便起见,不妨假设
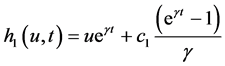 ,
, ,
,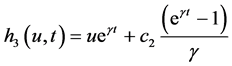
1) 当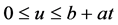 时,考虑一个非常小的时间区间
时,考虑一个非常小的时间区间 ,其中
,其中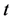 足够小,使得
足够小,使得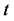 时刻的盈余达不到线性阈值
时刻的盈余达不到线性阈值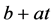 ,既有
,既有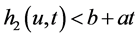 。考虑首次索赔时刻和索赔额,及索赔额是否导致绝对破产,可得
。考虑首次索赔时刻和索赔额,及索赔额是否导致绝对破产,可得
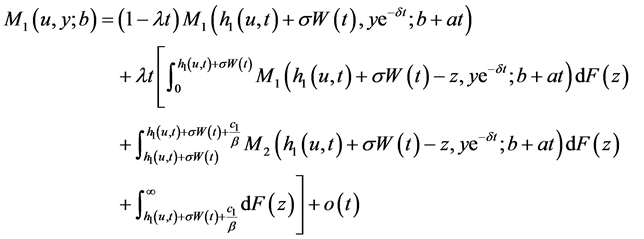 (13)
(13)
将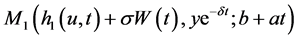 用Taylor展开有
用Taylor展开有
 (14)
(14)
将(14)带入(13)中,两边同除以 ,再令
,再令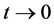 ,得到方程(5)。
,得到方程(5)。
2) 采用同样的方法,当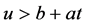 有
有
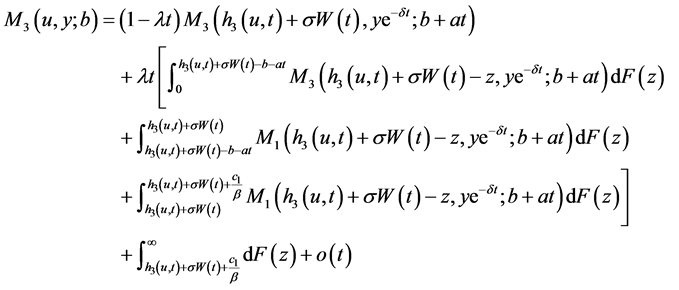 (15)
(15)
将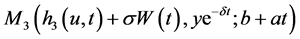 用Taylor展开有
用Taylor展开有
 (16)
(16)
将(16)带入(15)中,两边同除以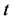 ,再令
,再令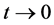 ,得到方程(6)。
,得到方程(6)。
3) 当 时,令
时,令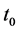 是方程
是方程 的根,即
的根,即 它表示在
它表示在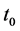 之前没有索赔发生时的盈余恢复到0水平的时刻,满足当
之前没有索赔发生时的盈余恢复到0水平的时刻,满足当 时有
时有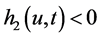 ,
,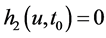 。另一方面当
。另一方面当 时,
时, 表示
表示 之前没有索赔发生时的盈余。利用首次索赔时刻和索赔额大小,由全概率公式有
之前没有索赔发生时的盈余。利用首次索赔时刻和索赔额大小,由全概率公式有
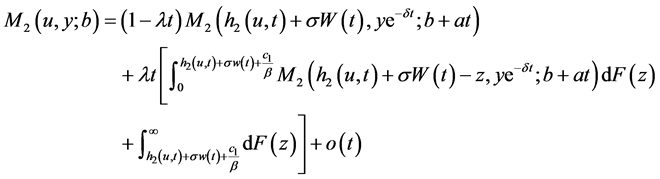 (17)
(17)
将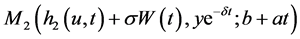 用Taylor展开有
用Taylor展开有
 (18)
(18)
将(18)带入(17)中,两边同除以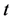 ,再令
,再令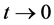 ,得到方程(7)。
,得到方程(7)。
下面验证边界条件:
当 时,则绝对破产即可发生,从而没有红利支付,因此(8)成立。
时,则绝对破产即可发生,从而没有红利支付,因此(8)成立。
当 时,则没有分红被支付,因此(9)成立。
时,则没有分红被支付,因此(9)成立。
当 时,
时, 。又因
。又因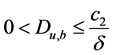 ,从而(10)成立。
,从而(10)成立。
对于(11)和(12),方法类似于Wan [10] 。
注2.1:在定理2.1中当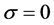 时,我们就得到带常利率投资和线性阈值分红策略下的绝对破产模型,即(3)所对应
时,我们就得到带常利率投资和线性阈值分红策略下的绝对破产模型,即(3)所对应 所满足的积分–微分方程。
所满足的积分–微分方程。
注2.2:在定理2.1中当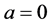 时,我们就得到带常利率投资和阈值分红策略下的带扰动的绝对破产模型,此结果类似于于文广 [11] 的博士论文。
时,我们就得到带常利率投资和阈值分红策略下的带扰动的绝对破产模型,此结果类似于于文广 [11] 的博士论文。
同样 可根据初始盈余的不同定义为
可根据初始盈余的不同定义为
 (19)
(19)
其中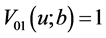 。
。
利用表示定理 可得
可得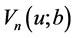 所满足的积分–微分方程。
所满足的积分–微分方程。
定理2.2. 当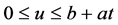 时有
时有
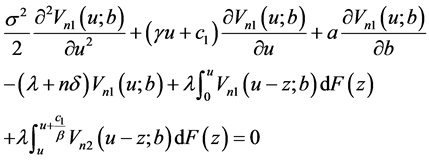 (20)
(20)
当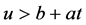 时有
时有
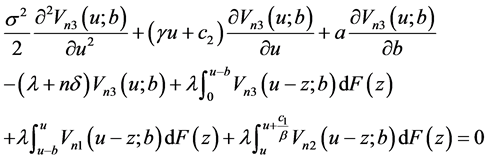 (21)
(21)
当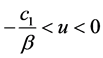 时有
时有
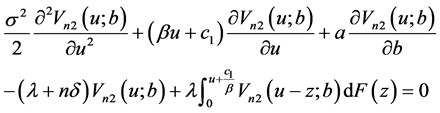 (22)
(22)
其中边界条件为
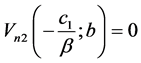 (23)
(23)
 (24)
(24)
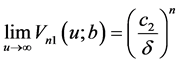 (25)
(25)
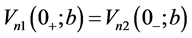 (26)
(26)
 (27)
(27)
证明:方法类似于定理2.1。
注2.3:在定理2.2中当 时,我们就得到带常利率投资和线性阈值分红策略下的绝对破产模型,即(3)所对应
时,我们就得到带常利率投资和线性阈值分红策略下的绝对破产模型,即(3)所对应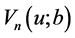 所满足的积分–微分方程。
所满足的积分–微分方程。
注2.4:在定理2.2中当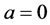 时,我们就得到带常利率投资和阈值分红策略下的带扰动的绝对破产模型,此结果类似于于文广 [11] 的博士论文。
时,我们就得到带常利率投资和阈值分红策略下的带扰动的绝对破产模型,此结果类似于于文广 [11] 的博士论文。
3. Gerber-Shiu期望折现罚金函数
在这部分中将给出著名的Gerber-Shiu期望折现罚金函数所满足的偏积分–微分方程。
由初始盈余的取值不同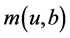 定义为
定义为
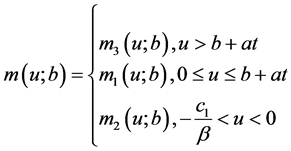 (28)
(28)
定理3.1. 当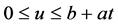 时有
时有
 (29)
(29)
当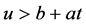 时有
时有
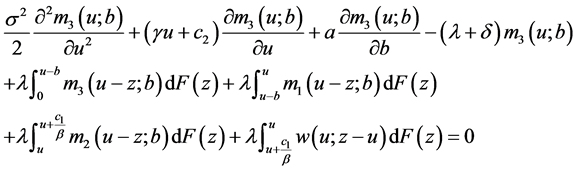 (30)
(30)
当 时有
时有
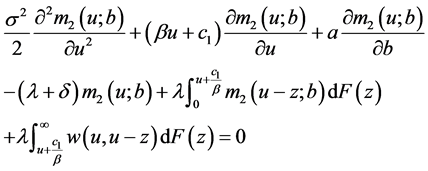 (31)
(31)
其中边界条件为
 (32)
(32)
 (33)
(33)
 (34)
(34)
证明:
1) 当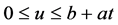 时,考虑一个非常小的时间区间
时,考虑一个非常小的时间区间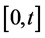 ,其中
,其中 足够小,使得
足够小,使得 时刻的盈余达不到线性阈值
时刻的盈余达不到线性阈值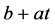 ,既有
,既有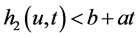 。考虑首次索赔时刻和索赔额,及索赔额是否导致绝对破产,可得
。考虑首次索赔时刻和索赔额,及索赔额是否导致绝对破产,可得
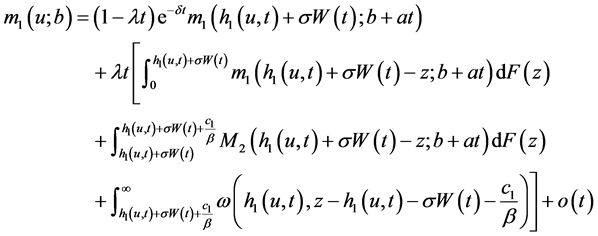 (35)
(35)
使用与(13)相似的方法可得(29)。
2) 采用同样的方法,当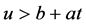 有
有
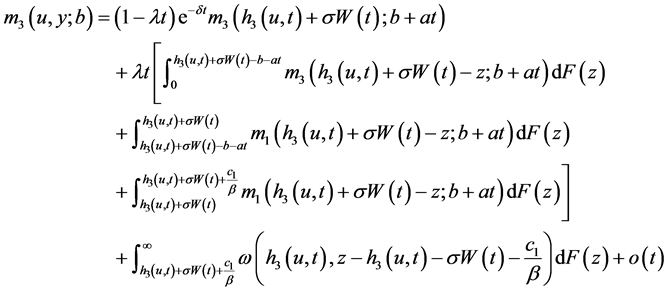 (36)
(36)
使用与(15)相似的方法可得(30)。
3) 当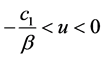 时,有
时,有
 (37)
(37)
使用与(17)相似的方法可得(31)。
边界条件可采用相同的方法得到。
注3.1:在定理3.1中当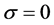 时,我们就得到带常利率投资和线性阈值分红策略下的绝对破产模型,即(3)所对应
时,我们就得到带常利率投资和线性阈值分红策略下的绝对破产模型,即(3)所对应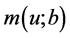 所满足的积分–微分方程。
所满足的积分–微分方程。
注3.2:在定理3.1中当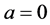 时,我们就得到带常利率投资和阈值分红策略下的带扰动的绝对破产模型,此结果类似于于文广 [11] 的博士论文。
时,我们就得到带常利率投资和阈值分红策略下的带扰动的绝对破产模型,此结果类似于于文广 [11] 的博士论文。
4. 结论
本文将投资策略采用常利率的投资和分红策略推广到线性阈值的分红策略两方面去研究绝对破产模型下的红利支付的矩母函数和红利支付的n-阶矩函数以及著名Gerber-Shiu期望折现罚金函数,更加接近真实市场。
基金项目
国家自然科学基金资助项目(11361058)。
文章引用
贺婷,吴黎军. 基于常利率投资和线性阈值分红策略下的绝对破产模型
The Absolute Ruin Risk Model with Constant Interest Investment and a Linear Threshold Dividend Strategy[J]. 统计学与应用, 2016, 05(01): 39-47. http://dx.doi.org/10.12677/SA.2016.51005
参考文献 (References)
- 1. Cramer, H. (1930) On the Mathematical Theory of Risk. Skandia Jubillee Volume, Stockholm.
- 2. Gerber, H.U. (1970) An Extension of the Renewal Equation and Its Application in the Collective Theory of Risk. Journal of Computational and Applied Mathematics, 3-4, 205-210. http://dx.doi.org/10.1080/03461238.1970.10405664
- 3. Gerber, H.U. and Yang, H. (2007) Absolute Rain Probabilities in a Jump Diffusion Risk Model with Investment. North American Actuarial Journal, 11, 159-169. http://dx.doi.org/10.1080/10920277.2007.10597474
- 4. Zeng, F.Z. and Xu, J.S. (2013) The Perturbed Dual Risk Model with Constant Interest and a Threshold Dividend Strategy. Abstract and Applied Analysis, 2013, Article ID: 981076. http://dx.doi.org/10.1155/2013/981076
- 5. 彭丹, 侯振挺, 刘再明. 常利率和门限分红策略下带干扰的poisson风险模型的绝对破产模型问题[J]. 应用数学学报, 2012, 35(5): 885.
- 6. De Finetti, B. (1957) Su un’impostazione alternativa dell teoria colletiva del rischio. Transactions of the XV International Congress of Actuaries, 2, 433-443.
- 7. 张燕, 寇冰煜, 毛磊. 线性红利边界下带干扰的风险模型的破产理论[J]. 西安工业大学学报, 2015, 35(1): 8-15.
- 8. Liu, D.H. and Liu, Z.M. (2011) The Perturbed Compound Poisson Risk Model with Linear Dividend Barrier. Journal of Computational and Applied Mathematics, 235, 2357-2363. http://dx.doi.org/10.1016/j.cam.2010.10.034
- 9. Gao, S. and Liu, Z.M. (2010) The Perturbed Compound Poisson Risk Model with Constant Interest and a Threshold Dividend Strategy. Journal of Computational and Applied Mathematics, 233, 2181-2188. http://dx.doi.org/10.1016/j.cam.2009.10.004
- 10. Wan, N. (2007) Dividend Payments with a Threshold Strategy in the Compound Poisson Risk Model Perturbed by Diffusion. Insurance: Mathematics and Economics, 40, 509-523. http://dx.doi.org/10.1016/j.insmatheco.2006.08.002
- 11. 于文广. 保险风险模型的破产理论与分红策略的研究[D]: [博士学位论文]. 济南: 山东大学, 2014.