Statistics and Application
Vol.06 No.01(2017), Article ID:19902,29
pages
10.12677/SA.2017.61005
The Sample Covariance Matrix and the Sample Correlation Matrix and Their Applications in the Sample Principal Component
Yingying Zhang, Tengzhong Rong
Department of Statistics and Actuarial Science, College of Mathematics and Statistics, Chongqing University, Chongqing
Received: Feb. 25th, 2017; accepted: Mar. 14th, 2017; published: Mar. 17th, 2017

ABSTRACT
We give the properties and proofs of the sample principal component, and discuss them in two different conditions: from S on to calculate principal component and from R on to calculate principal component. From S on to calculate principal component, we give 7 properties (S1)-(S7) and their proofs, and the relationships stated by these properties get full display in Figure 1. Similarly, from R on to calculate principal component, we give 7 properties (R1)-(R7) and their proofs, and the relationships stated by these properties get full display in Figure 2. Finally we give two numerical simulation examples to verify the correctness of properties (S1)-(S7) and (R1)-(R7).
Keywords:Sample Covariance Matrix, Sample Correlation Matrix, Sample Principal Component, Properties and Proofs, R Software
样本协方差矩阵和样本相关矩阵及其在样本主成分中的应用
张应应,荣腾中
重庆大学数学与统计学院统计与精算学系,重庆
收稿日期:2017年2月25日;录用日期:2017年3月14日;发布日期:2017年3月17日

摘 要
我们给出了样本主成分的性质及证明,分两种情况讨论:从S出发求主成分和从R出发求主成分。在从S出发求主成分中,给出了7个性质(S1)-(S7)及它们的证明,这些性质说明的关系在图1中得到了充分的展现。同样,在从R出发求主成分中,给出了7个性质(R1)-(R7)及它们的证明,这些性质说明的关系在图2中得到了充分的展现。最后我们给出了两个数值模拟的例子来验证性质(S1)-(S7)和(R1)-(R7)的正确性。
关键词 :样本协方差矩阵,样本相关矩阵,样本主成分,性质及证明,R软件

Copyright © 2017 by authors and Hans Publishers Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/


1. 引言
主成分分析(Principal Component Analysis, PCA)或称主分量分析,是一种降维的统计方法。通过正交变换将一组可能存在相关性的变量转换为一组线性不相关的综合变量,同时根据实际需要从中可以取出几个较少的综合变量尽可能多地反映原来变量的信息,转换后的这组综合变量叫主成分。主成分分析首先是由卡尔∙皮尔森(Karl Pearson)对非随机变量引入的,尔后霍特林将此方法推广到随机向量的情形。信息的大小通常用方差来衡量。
为研究总体主成分和样本主成分的性质,需要定义总体或样本的协方差(矩阵)和相关系数(矩阵)。它们的定义及性质请参见 [1] 。总体主成分的性质在 [2] - [10] 中已有很好的总结及证明,但是他们对样本主成分的性质讨论却不多。由于总体的协方差矩阵和相关系数矩阵一般是未知的,而样本资料阵一般是已知的,人们一般采用样本主成分进行计算,从而研究样本主成分的性质就显得非常重要。本文给出了样本主成分的性质及证明,分两种情况讨论:从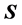 出发求主成分并给出了7个性质(S1)-(S7)及它们的证明;从
出发求主成分并给出了7个性质(S1)-(S7)及它们的证明;从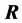 出发求主成分并给出了7个性质(R1)-(R7)及它们的证明。
出发求主成分并给出了7个性质(R1)-(R7)及它们的证明。
本文剩余部分安排如下:第2节给出样本主成分的性质及证明,分两种情况讨论:从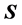 出发求主成分和从
出发求主成分和从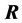 出发求主成分。这些性质(S1)-(S7)和(R1)-(R7)说明的关系在图1和图2中得到了充分的展现。第3节给出了两个数值模拟的例子来验证性质(S1)-(S7)和(R1)-(R7)的正确性。第4节总结。
出发求主成分。这些性质(S1)-(S7)和(R1)-(R7)说明的关系在图1和图2中得到了充分的展现。第3节给出了两个数值模拟的例子来验证性质(S1)-(S7)和(R1)-(R7)的正确性。第4节总结。
2. 样本主成分的性质及证明
有总体主成分和样本主成分,有协方差矩阵和相关矩阵,把这两个概念结合在一起形成表1。本文讨论样本主成分的性质及证明。分两种情况讨论:从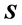 或
或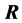 出发求主成分。
出发求主成分。
2.1. 从S出发求主成分
设 为样本协方差矩阵
为样本协方差矩阵 的特征值,
的特征值,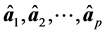 为相应的两两正交的单位特征向量,即
为相应的两两正交的单位特征向量,即
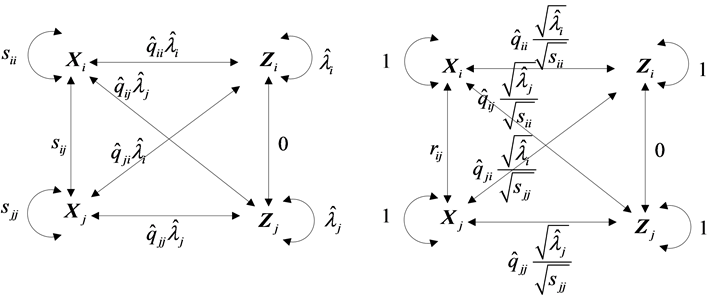
Figure 1. The relationships of the sample covariances (left) and the relationships of the sample correlations (right) among 
图1.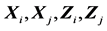 的样本协方差关系图(左)和样本相关系数关系图(右)
的样本协方差关系图(左)和样本相关系数关系图(右)

Figure 2. The relationships of the sample covariances (left) and the relationships of the sample correlations (right) among 
图2.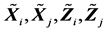 的样本协方差关系图(左)和样本相关系数关系图(右)
的样本协方差关系图(左)和样本相关系数关系图(右)
Table 1. The covariance matrix and the correlation matrix of the population and the sample
表1. 总体和样本的协方差矩阵和相关矩阵
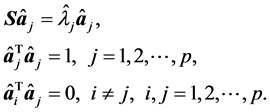
令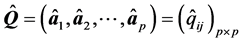 ,它是一个正交阵,
,它是一个正交阵,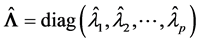 ,写成矩阵形式,就是
,写成矩阵形式,就是
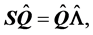
上式两边左乘以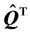 ,得到
,得到

则第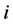 个主成分
个主成分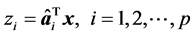 ,其中
,其中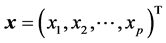 ,且
,且
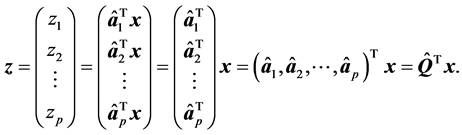
下面构造样本主成分,令

因此样本主成分为
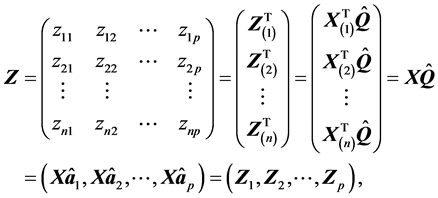
其中 表示样本主成分的各行,
表示样本主成分的各行, 表示样本主成分的各列。易知
表示样本主成分的各列。易知

类似于数据资料阵 的标准化 [1] ,可得到矩阵
的标准化 [1] ,可得到矩阵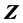 的标准化矩阵
的标准化矩阵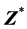 满足
满足
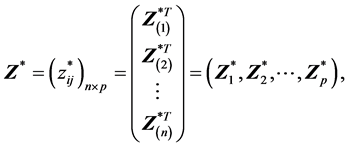
其中
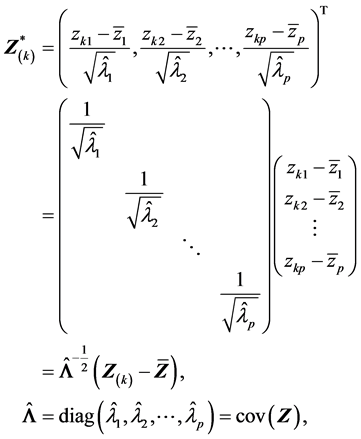
上式中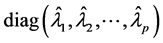 表示由向量
表示由向量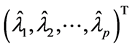 作为对角线元素构成的对角阵。注意,上式用到了(S2)的结论。从而
作为对角线元素构成的对角阵。注意,上式用到了(S2)的结论。从而
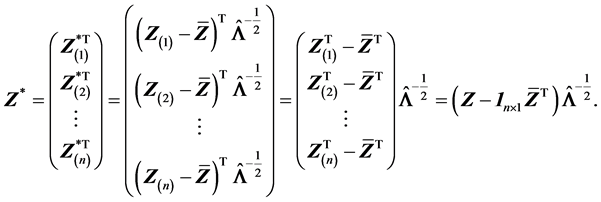
易知
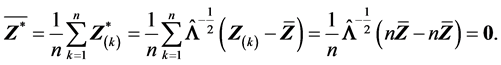
因为 ,人们自然会想到
,人们自然会想到 ,但是一般来说这是错误的。详细的证明请见本文的附录。
,但是一般来说这是错误的。详细的证明请见本文的附录。
我们用 表示它是一个非负定阵,用
表示它是一个非负定阵,用 表示它是一个正定阵。令
表示它是一个正定阵。令 为数据资料矩阵,
为数据资料矩阵,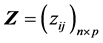 为主成分得分矩阵,则对于由
为主成分得分矩阵,则对于由 出发计算的样本主成分有如下性质:
出发计算的样本主成分有如下性质:
(S1).
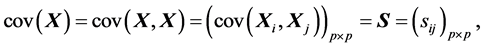
特别地,
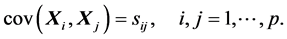
(S2).

特别地,
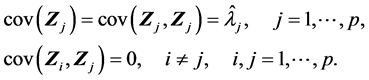
(S3).
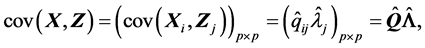
特别地,

(S4).
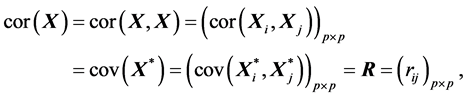
特别地,
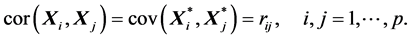
(S5). 若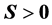 ,则
,则
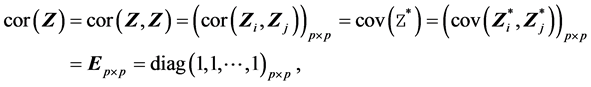
特别地,

(S6). 若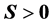 ,则
,则
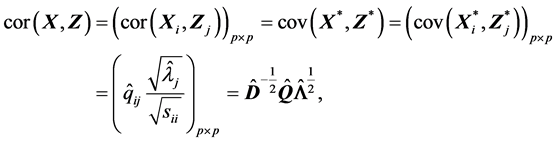
其中
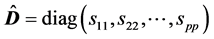
是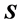 的对角线元素组成的对角阵。特别地,
的对角线元素组成的对角阵。特别地,
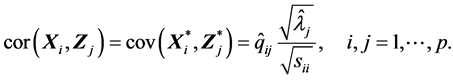
(S7). 样本总方差

此式表明了样本 的样本(协)方差之和等于样本主成分
的样本(协)方差之和等于样本主成分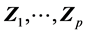 的样本(协)方差之和。
的样本(协)方差之和。
在以上7个性质中,(S1)显然,(S2)和(S6)的分量形式的结果和(S7)可以在 [7] 中找到。
注意,在(S5)和(S6)中我们要求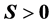 ,而其余性质只要求
,而其余性质只要求 。因为在(S5)和(S6)的证明中会涉及到
。因为在(S5)和(S6)的证明中会涉及到
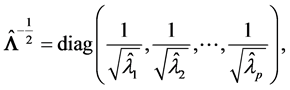
若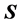 有一个0特征值,即
有一个0特征值,即 ,则
,则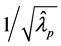 是没有意义的,从而结论不成立,数值结果也证实了这一点。
是没有意义的,从而结论不成立,数值结果也证实了这一点。
由性质(S1)-(S6)归纳得到样本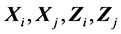 的样本协方差关系图((S1)-(S3))和样本相关系数关系图((S4)-(S6)),如图1。
的样本协方差关系图((S1)-(S3))和样本相关系数关系图((S4)-(S6)),如图1。
性质(S1)-(S7)的证明有些是初等的,有些需要一定的技巧,由于这些证明较占篇幅,所以把它们放到了本文的附录中。
2.2. 从R出发求主成分
设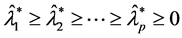 为样本相关矩阵
为样本相关矩阵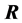 的特征值,
的特征值,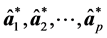 为相应的两两正交的单位特征向量,即
为相应的两两正交的单位特征向量,即
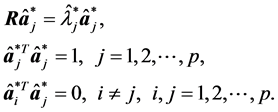
令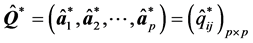 ,它是一个正交阵,
,它是一个正交阵, ,写成矩阵形式,就是
,写成矩阵形式,就是

上式两边左乘以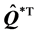 ,得到
,得到

则第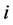 个主成分
个主成分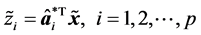 ,其中
,其中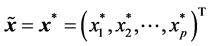 。这是因为我们从样本相关矩阵
。这是因为我们从样本相关矩阵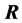 出发,所以变量已经标准化了。且
出发,所以变量已经标准化了。且

下面构造样本主成分,令

则

因此样本主成分为

其中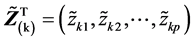 表示样本主成分的各行,
表示样本主成分的各行, 表示样本主成分的各列。注意到
表示样本主成分的各列。注意到

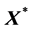 和
和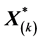 可参照 [1] 中的数据资料矩阵
可参照 [1] 中的数据资料矩阵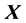 的标准化部分。但是,
的标准化部分。但是,

所以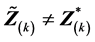 ,从而
,从而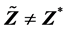 。易知
。易知

容易验证
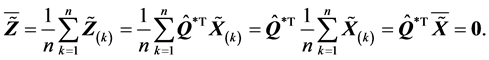
由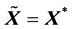 和
和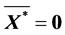 有
有

其中
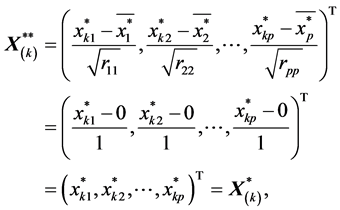
注意,上式用到了(S4)的结论 。则
。则

易知

类似于矩阵 的标准化,可得到矩阵
的标准化,可得到矩阵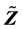 的标准化矩阵
的标准化矩阵 满足
满足

其中

注意,上式用到了(R2)的结论。从而
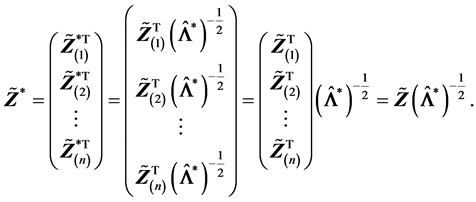
易知

因为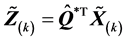 ,人们自然会想到
,人们自然会想到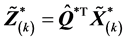 ,同样,一般来说这是错误的。详细的证明请见本文的附录。
,同样,一般来说这是错误的。详细的证明请见本文的附录。
值得一提的是,矩阵 和它的标准化矩阵
和它的标准化矩阵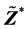 的推导是新的。
的推导是新的。
我们用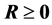 表示它是一个非负定阵,
表示它是一个非负定阵,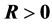 表示它是一个正定阵。令
表示它是一个正定阵。令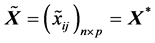 为数据资料矩阵,
为数据资料矩阵,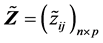 为主成分得分矩阵,则对于由
为主成分得分矩阵,则对于由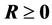 出发计算的样本主成分有如下性质:
出发计算的样本主成分有如下性质:
(R1).
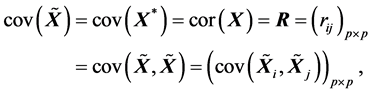
特别地,
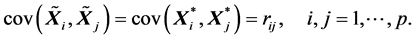
(R2).

特别地,
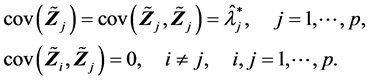
(R3).
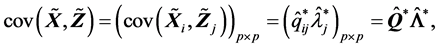
特别地,
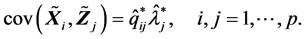
(R4).
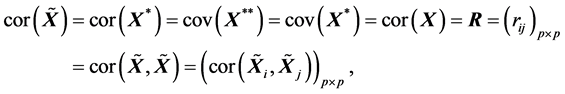
特别地,对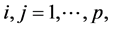
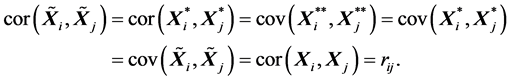
(R5). 若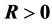 ,则
,则

特别地,
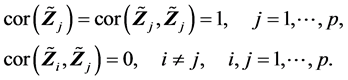
(R6). 若 ,则
,则
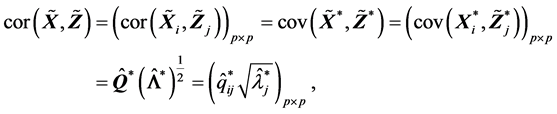
特别地,
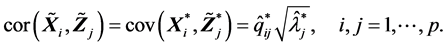
(R7). 样本总方差

此式表明了样本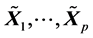 的样本(协)方差之和等于样本主成分
的样本(协)方差之和等于样本主成分 的样本(协)方差之和。
的样本(协)方差之和。
在以上7个性质中,(R1)显然,(R2)和(R6)的分量形式的结果和(R7)可以在 [7] 中找到。
注意,在(R5)和(R6)中我们要求 ,而其余性质只要求
,而其余性质只要求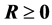 。因为在(R5)和(R6)的证明中会涉及到
。因为在(R5)和(R6)的证明中会涉及到

若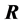 有一个0特征值,即
有一个0特征值,即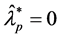 ,则
,则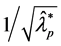 是没有意义的,从而结论不成立,数值结果也证实了这一点。
是没有意义的,从而结论不成立,数值结果也证实了这一点。
由性质(R1)-(R6)归纳得到样本 的样本协方差关系图((R1)-(R3))和样本相关系数关系图((R4)-(R6)),如图2。
的样本协方差关系图((R1)-(R3))和样本相关系数关系图((R4)-(R6)),如图2。
性质(R1)-(R7)的证明有些是初等的,有些需要一定的技巧,由于这些证明较占篇幅,所以把它们放到了本文的附录中。
3. 数值模拟
此节我们在R软件 [11] 中编写程序,通过数值模拟来验证从样本协方差矩阵 出发计算的样本主成分的性质(S1)-(S7)及从样本相关矩阵
出发计算的样本主成分的性质(S1)-(S7)及从样本相关矩阵 出发计算的样本主成分的性质(R1)-(R7)。
出发计算的样本主成分的性质(R1)-(R7)。
在R软件中,求矩阵的样本协方差矩阵的函数是cov(),求矩阵的样本相关矩阵的函数是cor() [12] 。性质(S1)-(S7)即是要验证
(S1). 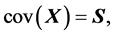 (S2).
(S2). 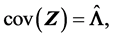 (S3).
(S3). 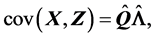
(S4). 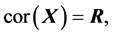 (S5).
(S5). 
(S6). 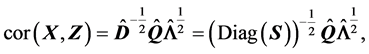
(S7). 
注意在(S1)中的 和(S4)中的
和(S4)中的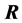 分别为
分别为
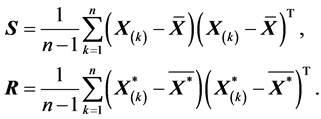
性质(R1)-(R7)即是要验证
(R1). 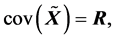 (R2).
(R2). 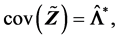 (R3).
(R3). 
(R4). 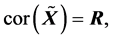 (R5).
(R5). 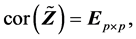
(R6).  (R7).
(R7). 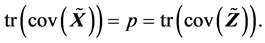
注意在(S5)和(S6)中要求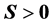 ,在(R5)和(R6)中要求
,在(R5)和(R6)中要求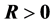 。
。
下面我们举两个例子来验证(S1)-(S7)和(R1)-(R7)的正确性。
例1.
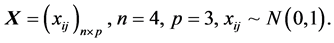
为重复本文的结果,我们在R软件中使用set.seed(1),此时
 .
.
容易验证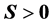 且
且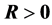 ,(S1)-(S7)和(R1)-(R7)均是正确的。详细的数值模拟结果请见本文的附录。
,(S1)-(S7)和(R1)-(R7)均是正确的。详细的数值模拟结果请见本文的附录。
下面给一个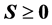 且
且 的例子,即
的例子,即 和
和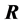 都有1个0特征值,此时(S5),(S6),(R5)和(R6)是不成立的,但其余性质是成立的。
都有1个0特征值,此时(S5),(S6),(R5)和(R6)是不成立的,但其余性质是成立的。
例2.

为重复本文的结果,我们在R软件中使用set.seed(1),此时

详细的数值模拟结果请见本文的附录。
4. 总结
我们给出了样本主成分的性质及证明,分两种情况讨论:从 出发求主成分和从
出发求主成分和从 出发求主成分。在从
出发求主成分。在从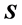 出发求主成分中,给出了7个性质(S1)-(S7)及它们的证明,这些性质说明的关系在图1中得到了充分的展现。同样,在从
出发求主成分中,给出了7个性质(S1)-(S7)及它们的证明,这些性质说明的关系在图1中得到了充分的展现。同样,在从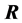 出发求主成分中,给出了7个性质(R1)-(R7)及它们的证明,这些性质说明的关系在图2中得到了充分的展现。最后我们给出了两个数值模拟的例子来验证性质(S1)-(S7)和(R1)-(R7)的正确性。例1中的
出发求主成分中,给出了7个性质(R1)-(R7)及它们的证明,这些性质说明的关系在图2中得到了充分的展现。最后我们给出了两个数值模拟的例子来验证性质(S1)-(S7)和(R1)-(R7)的正确性。例1中的 且
且 ,从而性质(S1)-(S7)和(R1)-(R7)均是正确的。例2中的
,从而性质(S1)-(S7)和(R1)-(R7)均是正确的。例2中的 且
且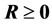 ,即
,即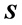 和
和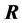 都有1个0特征值,数值模拟显示(S5),(S6),(R5)和(R6)是不成立的,但其余性质是成立的,与理论结果相一致。
都有1个0特征值,数值模拟显示(S5),(S6),(R5)和(R6)是不成立的,但其余性质是成立的,与理论结果相一致。
基金项目
本研究受中央高校基本科研业务费项目(CQDXWL-2012-004; CDJRC10100010),中国国家留学基金(201606055028)和教育部人文社会科学研究西部和边疆地区项目(14XJC910001)支持。
文章引用
张应应,荣腾中. 样本协方差矩阵和样本相关矩阵及其在样本主成分中的应用
The Sample Covariance Matrix and the Sample Correlation Matrix and Their Applications in the Sample Principal Component[J]. 统计学与应用, 2017, 06(01): 34-62. http://dx.doi.org/10.12677/SA.2017.61005
参考文献 (References)
- 1. 张应应. 总体或样本的协方差(矩阵)和相关系数(矩阵)的系统定义[J]. 统计与决策, 2016(8): 20-24.
- 2. 杨虎, 刘琼荪, 钟波. 数理统计[M]. 北京: 高等教育出版社, 2004.
- 3. 高惠璇. 应用多元统计分析[M]. 北京: 北京大学出版社, 2005.
- 4. Johnson, R.A. and Wichern, D.W. (2007) Applied Multivariate Statistical Analysis. 6th Edition, Pearson, Hoboken.
- 5. 汤银才. R语言与统计分析[M]. 北京: 高等教育出版社, 2008.
- 6. 王学民. 应用多元分析[M]. 第3版. 上海: 上海财经大学出版社, 2009.
- 7. 薛毅, 陈立萍. 统计建模与R软件[M]. 北京: 清华大学出版社, 2009.
- 8. 任雪松, 于秀林. 多元统计分析[M]. 第2版. 北京: 中国统计出版社, 2011.
- 9. 何晓群. 多元统计分析[M]. 第3版. 北京: 中国人民大学出版社, 2012.
- 10. 李素兰. 数据分析与R软件[M]. 北京: 科学出版社, 2013.
- 11. R Core Team (2017) R: A Language and Environment for Statistical Computing. R Foundation for Statistical Computing, Vienna, Austria. http://www.R-project.org/
- 12. Becker, R.A., Chambers, J.M. and Wilks, A.R. (1988) The New S Language. Wadsworth & Brooks/Cole.
附录
附录中包含了性质(S1)-(S7)和(R1)-(R7)的证明,还有两个例子的详细的数值模拟结果。
A.1. 准备知识及杂项证明
准备知识
样本的协方差(矩阵)和相关系数(矩阵)的定义及性质请参见 [1] 。 [1] 中有三个公式在本文中经常用到:
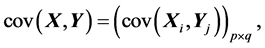 (A.1)
(A.1)
 (A.2)
(A.2)
其中 表示取矩阵
表示取矩阵 的对角线元素构成的对角阵,
的对角线元素构成的对角阵,
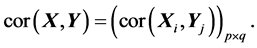 (A.3)
(A.3)
另外,还有
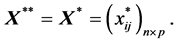 (A.4)
(A.4)
杂项证明
因为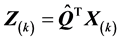 ,人们自然会想到
,人们自然会想到 ,但是一般来说这是错误的。从 [1] 中,我们知道
,但是一般来说这是错误的。从 [1] 中,我们知道

其中,
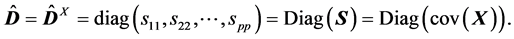
易知

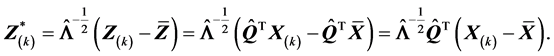
则
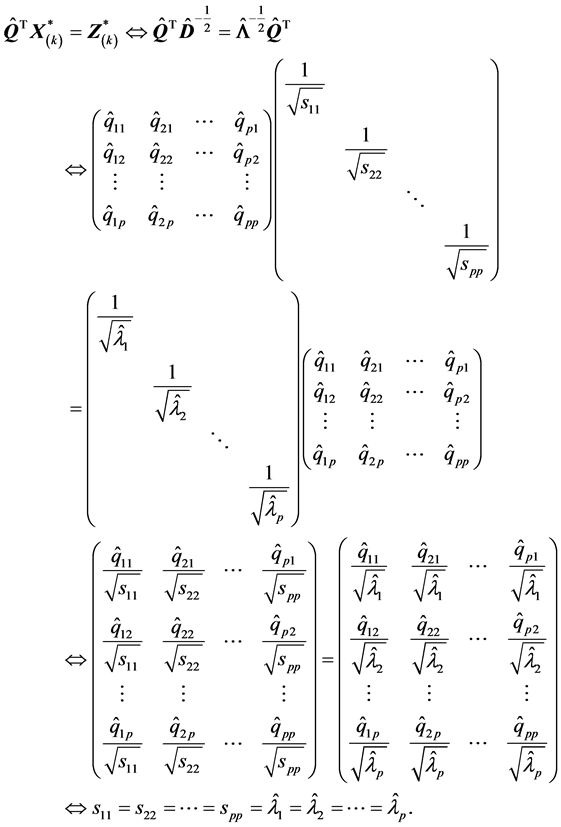
上式一般来说是不会一定成立的,所以一般来说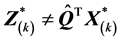 。
。
因为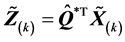 ,人们自然会想到
,人们自然会想到 ,同样,一般来说这是错误的。我们有
,同样,一般来说这是错误的。我们有

则
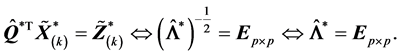
同样,上式一般来说是不会一定成立的,所以一般来说 。
。
A.2. 从S出发求主成分
证明:
(S1). 由数据资料阵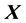 的样本协方差矩阵的定义有
的样本协方差矩阵的定义有

由(A.1)得,

从而,
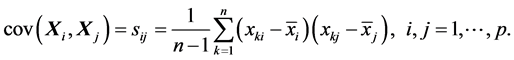
(S2). 易知
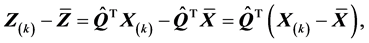
从而由矩阵 的样本协方差矩阵的定义有
的样本协方差矩阵的定义有

由(A.1)得
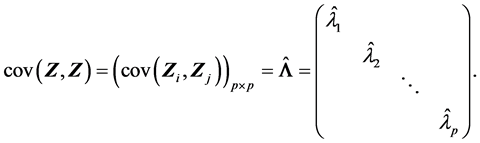
从而
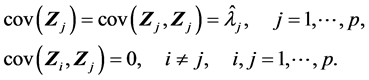
在证明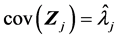 时,我们也可以利用样本协方差的定义直接来求。
时,我们也可以利用样本协方差的定义直接来求。

从而

因此

类似地,在证明 时,我们也可以利用样本协方差的定义直接来求。
时,我们也可以利用样本协方差的定义直接来求。


因此对
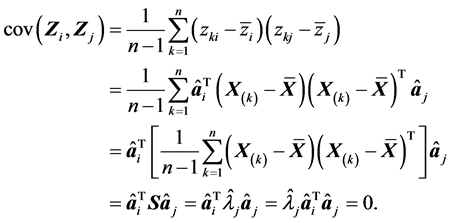
由此我们发现用矩阵形式来证明比用分量形式来证明要简洁得多。
(S3). 由(A.1),得
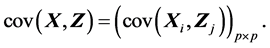
由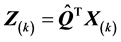 ,得
,得
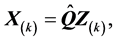 (A.5)
(A.5)
即
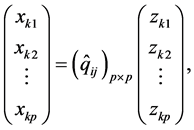
则
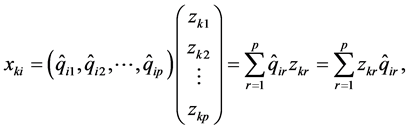
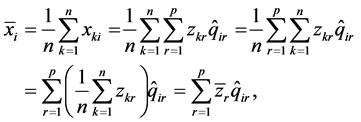
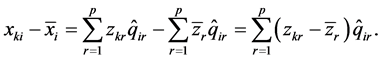
因此

上式最后两个等式用到了性质(S2)的结果。从而有
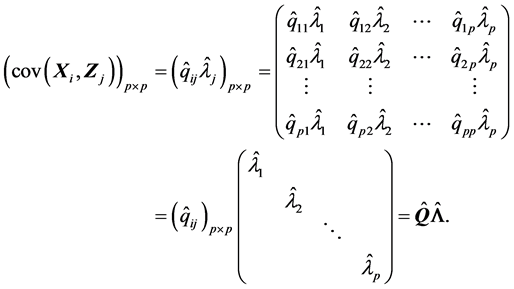
在证明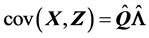 时也可以利用矩阵化的方法来证明。由(A.5),有
时也可以利用矩阵化的方法来证明。由(A.5),有
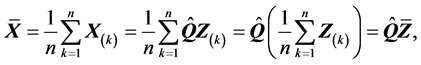
则
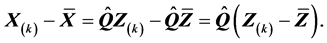
从而有
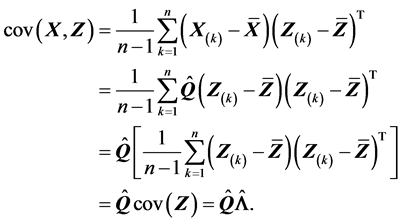
上式最后一个等式用到了性质(S2)的结果。由此发现矩阵化可以大大简化证明。
(S4). 由数据资料阵 的样本相关矩阵的定义有
的样本相关矩阵的定义有
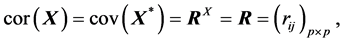
由(A.1),有

由(A.3),有
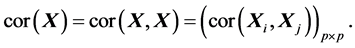
从而有
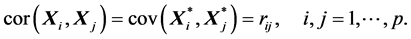
(S5). 由矩阵的样本相关矩阵的定义和(A.1)有

由(A.3)有
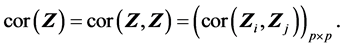
由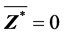 和(S2)的结论有
和(S2)的结论有
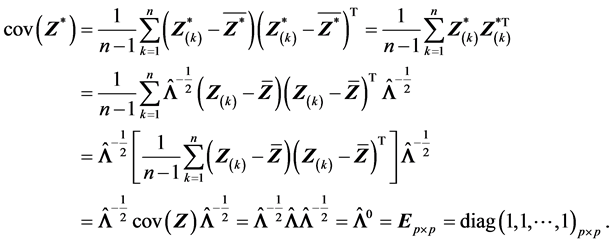
其实我们也可以利用(A.2)和(S2)的结论来证明
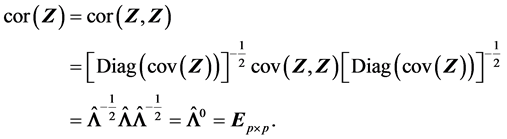
由此发现式(A.2)在求相关矩阵时非常有力,原因在于它使得我们可以利用已有的结论(S2)来简化证明。式(A.2)在(S6),(R4)-(R6)的证明中求相关矩阵时都会用到。从而
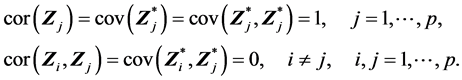
(S6). 由(A.3)有

由矩阵的样本相关矩阵的定义和(A.1)有

容易验证
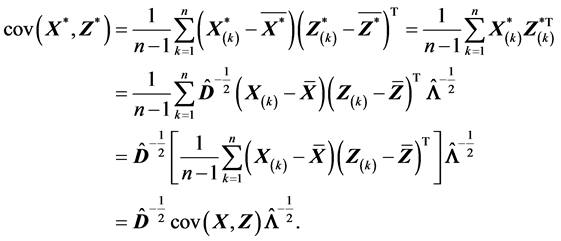
由(S3)知
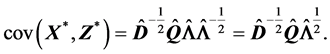
其实我们也可以利用(A.2)和(S1)-(S3)的结论来证明
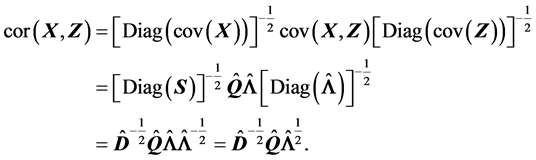
易知

从而有
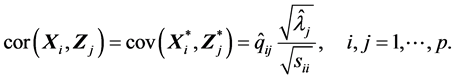
(S7). 由性质(S1)有

由性质(S2)有

由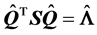 有
有

A.3. 从R出发求主成分
证明:
(R1). 由(A.1)有

由 及性质(S4)有
及性质(S4)有

从而有
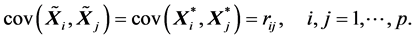
(R2). 由(A.1)有

由于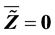 ,则
,则
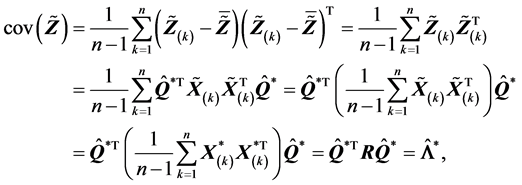
从而

(R3). 由(A.1)有

由于

从而

上式的最后一个等式在(R2)中已证明,从而由(R2)的结果有
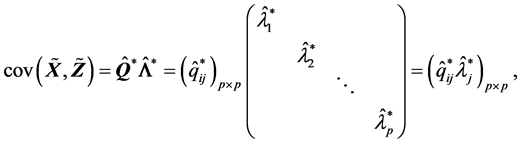
从而
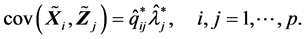
(R4). 由(A.3)有
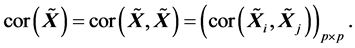
由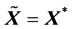 及矩阵的样本相关阵的定义有
及矩阵的样本相关阵的定义有

由性质(S4)有
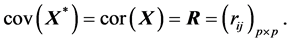
由(A.4)有

其实我们也可以利用(A.2)和(R1)的结论来证明
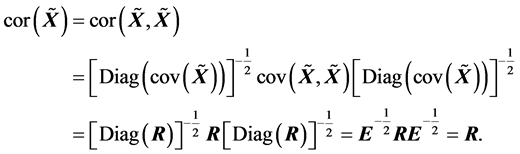
从而对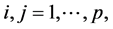

(R5). 由(A.3)有
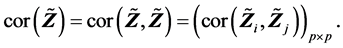
由矩阵的样本相关阵的定义有
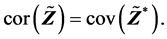
容易验证
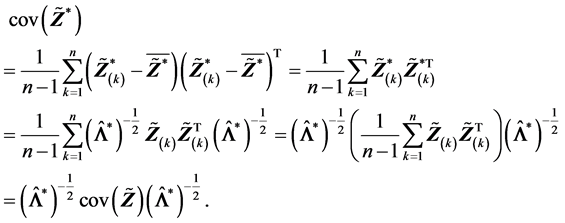
由性质(R2)的结果有
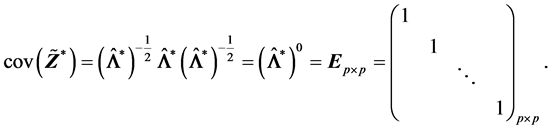
其实我们也可以利用(A.2)和(R2)的结论来证明

从而

(R6). 由(A.3)有

由 ,(A.4)和(A.1)有
,(A.4)和(A.1)有
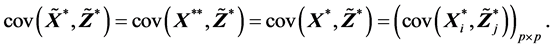
由矩阵的样本相关阵的定义有
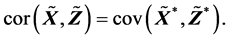
容易验证

再由性质(R3)的结果有

其实我们也可以利用(A.2)和(R1)-(R3)的结论来证明

易知
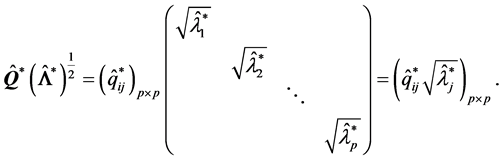
从而有

(R7). 由(R1)有
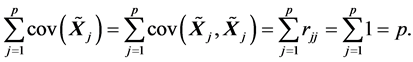
由(R2)有
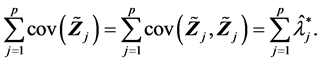
由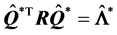 有
有
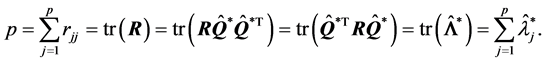
A.4. 数值模拟
在这里给出例1和例2的详细的数值模拟结果。
下面我们举两个例子来验证(S1)-(S7)和(R1)-(R7)的正确性。
例1.
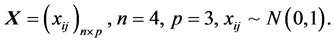
为重复本文的结果,我们在R软件中使用set.seed(1),此时
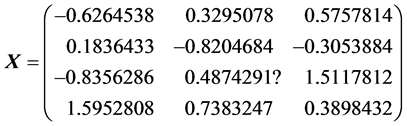
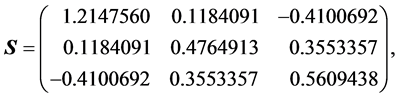
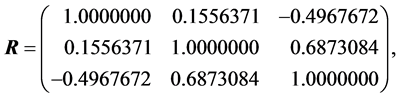
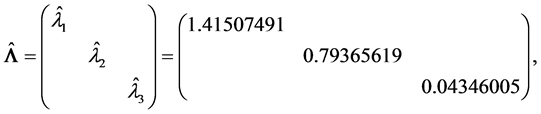
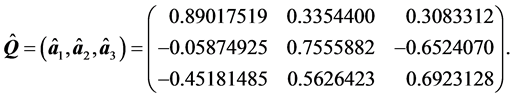
由于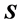 的特征值全为正,故
的特征值全为正,故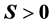 。
。
(S1).

(S2).
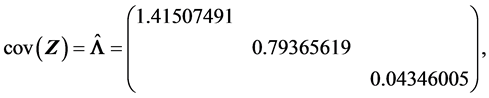
(S3).

(S4).

(S5).
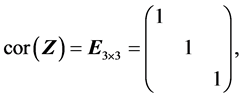
(S6).
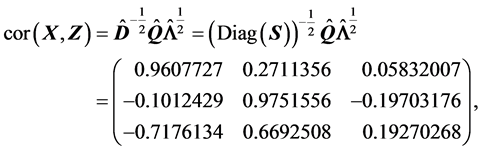
(S7).
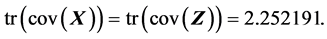
此时
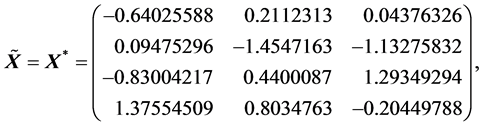
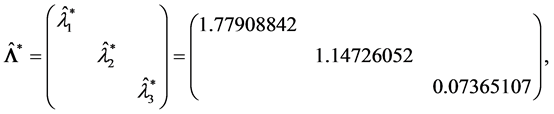
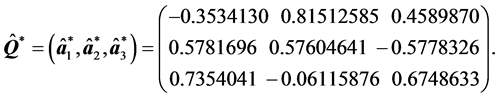
由于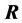 的特征值全为正,故
的特征值全为正,故 。
。
(R1).
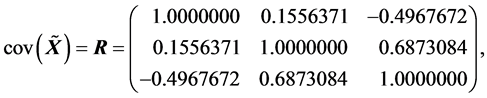
(R2).
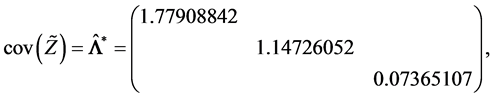
(R3).
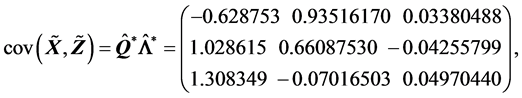
(R4).
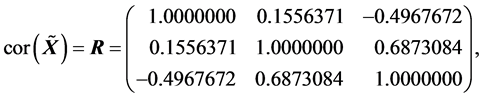
(R5).
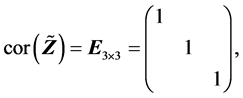
(R6).

(R7).
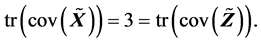
由数值结果可以看出,(S1)-(S7)和(R1)-(R7)均是正确的。
下面给一个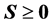 且
且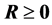 的例子,即
的例子,即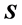 和
和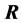 都有1个0特征值,此时(S5),(S6),(R5)和(R6)是不成立的,但其余性质是成立的。
都有1个0特征值,此时(S5),(S6),(R5)和(R6)是不成立的,但其余性质是成立的。
例2.
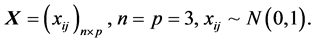
为重复本文的结果,我们在R软件中使用set.seed(1),此时
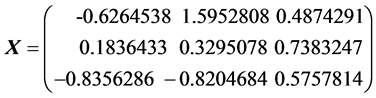
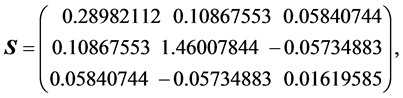

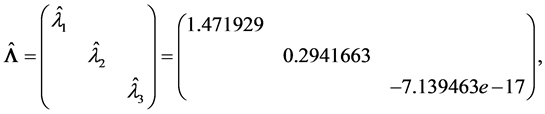
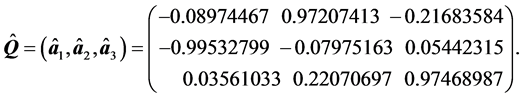
由于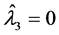 ,故
,故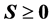 。
。
(S1).

(S2).
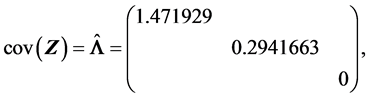
(S3).

(S4).
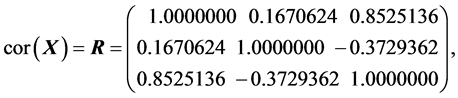
(S5).

(S6).
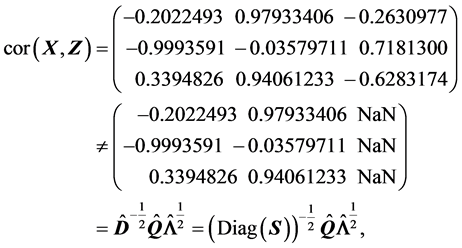
(S7).

此时
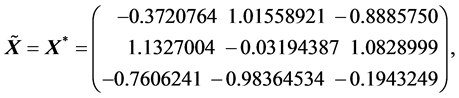
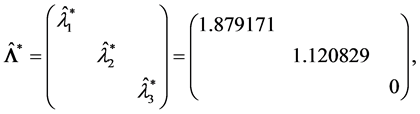
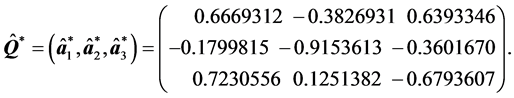
由于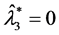 ,故
,故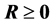 。
。
(R1).
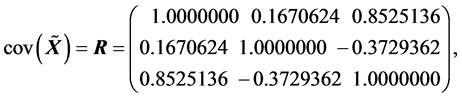
(R2).
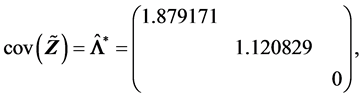
(R3).
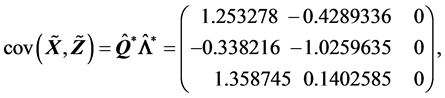
(R4).
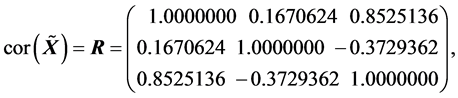
(R5).
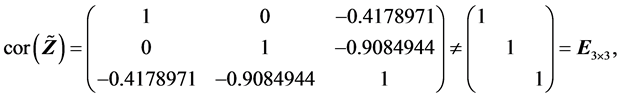
(R6).

(R7).

由数值结果可以看出,除了(S5),(S6),(R5)和(R6)之外,(S1)-(S4),(S7)和(R1)-(R4),(R7)均是正确的。
期刊投稿者将享受如下服务:
1.投稿前咨询服务 (QQ、微信、邮箱皆可)
2.为您匹配最合适的期刊
3.24小时以内解答您的所有疑问
4.友好的在线投稿界面
5.专业的同行评审
6.知网检索
7.全网络覆盖式推广您的研究
投稿请点击:http://www.hanspub.org/Submission.aspx
期刊邮箱:sa@hanspub.org
