Statistics and Application
Vol.06 No.02(2017), Article ID:21022,10
pages
10.12677/SA.2017.62017
The Optimal Reinsurance under the Marginal Indemnification Function and the Default Risk
Junhong Du*, Lijun Wu#
College of Mathematics and System Sciences, Xinjiang University, Urumqi Xinjiang
*第一作者。
#通讯作者。

Received: May 18th, 2017; accepted: Jun. 15th, 2017; published: Jun. 19th, 2017

ABSTRACT
In this paper, we consider the default risk of reinsurer. Firstly, we use the distortion risk measure and distortion premium principle to establish the total risk model with default risk. Secondly, by the relationship between the Marginal Indemnification Function (MIF) and the ceded loss function, we build MIF reinsurance optimization model equivalent to total risk model. Then, the optimal MIF function is obtained by solving the MIF reinsurance optimization model. Furthermore, the optimal ceded loss function is obtained. Finally, we apply this method to study the optimal loss function by the VaR risk measure and Wang’s premium principle.
Keywords:Optimal Reinsurance, Default Risk, Marginal Indemnification Function, Distortion Risk Measure, Reinsurance Premium, VaR Risk Measure, Wang’s Premium Principle
边际赔偿函数和违约风险下的 最优再保险
杜军红*,吴黎军#
新疆大学数学与系统科学学院,新疆 乌鲁木齐

收稿日期:2017年5月18日;录用日期:2017年6月15日;发布日期:2017年6月19日

摘 要
本文考虑了再保险人的违约风险,首先运用失真风险度量和失真保费原理建立了含有违约风险的总风险模型。其次通过边际索赔(MIF)函数与分出函数之间的关系建立了与总风险模型等价的MIF再保险优化模型。然后对MIF再保险优化模型的求解得到最优的边际索赔(MIF)函数,进而得到最优的分出函数。最后应用该方法研究了在VaR风险度量和Wang’s保费原理下的最优分出函数。
关键词 :最优再保险,违约风险,边际赔偿函数,失真风险度量,再保险保费,VaR风险度量,Wang’s保费原理

Copyright © 2017 by authors and Hans Publishers Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/


1. 引言
对于保险人,再保险是重要的风险管理工具,并且在精算领域的研究非常广泛。保险人分出一部分风险给再保险人来减少自己的风险责任,同时再保险人向保险人收取一定的保费来支付未来可能的索赔。最优再保险是在一个优化标准下去确定最优的分出风险。在不同的在保险合同中最优的分出风险有停止损失、比例损失、变换损失、限额停止损失以及有限截断停止损失等。Borch (1960) [1] 通过方差最小模型来研究再保险,在期望保费原理下,使得保险人自留风险的方差最小得到停止损失再保险是最优的。Arrow (1963) [2] 研究了在期望效用模型下的最优再保险。Young (1999) [3] 运用Wang’s保费原理推广了Arrow (1963)的结果。Kaluszkal (2001) [4] 在均值–方差保费原理下推广了Borch (1960)的结果。
在最近的研究中,Cai (2007) [5] 介绍了两类最优再保险模型,在期望保费原理下,通过风险度量VaR和CTE使得保险人的总风险最小来研究停止损失函数的最优自留额。Cai (2008) [6] ,Cheung (2010) [7] 和Tan (2011) [8] 在期望保费原理下,通过风险度量VaR和CVaR使得保险人的总风险最小来研究最优的分出函数的具体形式。Chi和Tan (2013) [9] 应用VaR和CVaR研究了一类保持凸序的保费原理下的最优再保险。Cui和Yang (2013) [10] 推导了一般的失真风险度量和失真保费原理下最优再保险,但是假定的失真函数是分段凸或者凹的。Zheng和Cui (2015) [11] 运用失真风险度量和期望保费原理来研究最优再保险。Cai (2014) [12] 考虑了初始资本和违约风险对再保险的影响,在期望保费原理下分别应用期望–效用模型和风险度量VaR来得到最优的分出风险。Assa (2014) [13] 首次应用边际索赔函数(Marginal Indemnification Function)来研究在失真风险度量和失真保费原理下的最优再保险。Zhuang和Weng (2016) [14] 首先再保险保费进行一定的限制,然后在失真风险度量和失真保费原理下应用边际索赔函数(MIF)和拉格朗日对偶方法研究了最优再保险。本文在Zhuang和Weng (2016)的基础之上考虑了再保险人违约风险,建立违约风险的最优化模型,在失真风险度量和失真保费原理下运用MIF函数研究了最优再保险。
文章的结构安排如下:第2节建立了违约风险的最优再保险模型。第3节研究了失真风险度量下的最优再保险以及对应的最优分出风险。第4节对风险度量VaR和Wang’s保费原理的实例分析。第5节是全文的总结。
2. 模型的建立
本文中,所有的随机变量均定义在概率空间 ,假设保险人面对的损失在一个固定时间下是非负的随机变量
,假设保险人面对的损失在一个固定时间下是非负的随机变量 ,对应的分布函数为
,对应的分布函数为 ,生存函数
,生存函数 ,并且
,并且 。记
。记 ,随机变量
,随机变量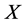 的有效域记为
的有效域记为 ,如果
,如果 ,即
,即 ,本文所有的结果也均成立。
,本文所有的结果也均成立。
在建立模型之前,首先引入失真风险度量以及失真保费原理的相关概念。
2.1. 失真风险度量和失真保费原理
我们称函数 是失真函数,如果它是满足:
是失真函数,如果它是满足:
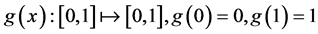
并且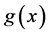 是非减左连续的实值函数。
是非减左连续的实值函数。
定义1 对于非负的随机变量 和失真函数
和失真函数 ,定义失真风险度量
,定义失真风险度量
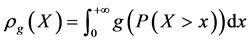 。
。
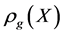 满足如下性质:
满足如下性质:
(1) 同单调可加性: ,对任意两个同单调的随机变量
,对任意两个同单调的随机变量 和
和 。
。
(2) 平移不变性: ,对任意的
,对任意的 和随机变量
和随机变量 。
。
(3) 单调性: ,当随机变量
,当随机变量 。
。
关于失真风险度量的具体讨论见Dhaene等(2006) [5] 。
当失真函数 给出不同的形式时,失真风险度量包含许多其他类型的风险度量。两个主要的例子就是
给出不同的形式时,失真风险度量包含许多其他类型的风险度量。两个主要的例子就是 和
和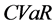 ,给出如下定义:
,给出如下定义:
定义 2 对于随机变量 ,给定置信水平
,给定置信水平 ,我们定义
,我们定义
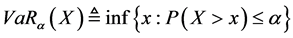 。
。
和
 。
。
对于失真风险度量,当 (其中
(其中 是示性函数),
是示性函数),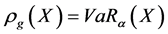 ,当
,当 ,
,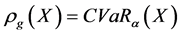 。
。
对于风险度量 ,
, 。当
。当 ,有
,有 ,为此我们规定参数
,为此我们规定参数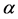 满足
满足 。另外,对于任意左连续的增函数
。另外,对于任意左连续的增函数 ,
,
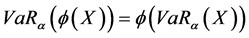 。
。
假定再保险保费是失真保费原理,它的定义如下:
定义 3失真保费原理定义为
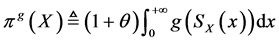 (1)
(1)
其中: 代表相对安全加载,
代表相对安全加载,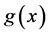 为失真函数。
为失真函数。
特别地,当 ,失真保费原理就是期望保费原理,即
,失真保费原理就是期望保费原理,即 。
。
当 是增的凹函数且
是增的凹函数且 ,失真保费原理就是Wang’s保费原理。
,失真保费原理就是Wang’s保费原理。
2.2. 初始资本和违约风险的再保险模型
在再保险合同中,保险人同意支付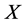 的部分损失
的部分损失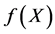 ,则对应保险人的自留损失为
,则对应保险人的自留损失为 。因此称
。因此称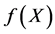 和
和 分别分出损失函数和自留损失函数。当保险人考虑再保险人的初始资本和违约风险时,对于分出的损失
分别分出损失函数和自留损失函数。当保险人考虑再保险人的初始资本和违约风险时,对于分出的损失 ,我们用失真风险度量
,我们用失真风险度量 来确定再保险人的初始资本
来确定再保险人的初始资本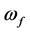 ,即
,即
 。
。
用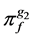 表示再保险保费,根据(1)式,即
表示再保险保费,根据(1)式,即
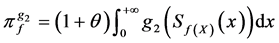 。
。
对于再保险人的赔偿,保险人意识到存在一定的潜在风险。如果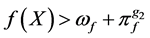 ,但再保险人仅赔付
,但再保险人仅赔付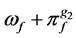 ,显然保险人会出现亏损,如果
,显然保险人会出现亏损,如果 ,再保险人仅赔付
,再保险人仅赔付 ,则就是一般研究的经典的风险模型。因此,在考虑违约风险的情况下保险人的总风险可以表示为:
,则就是一般研究的经典的风险模型。因此,在考虑违约风险的情况下保险人的总风险可以表示为:
 ,
,
其中 。
。
2.3. 分出损失函数集的建立
假定再保险合同中分出函数 满足下面两个条件:
满足下面两个条件:
(i) 且
且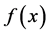 是非减函数。
是非减函数。
(ii)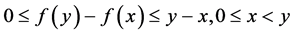 。
。
在这篇文章中,所有的分出函数均满足条件(i) (ii),记
 。
。
由于分出函数 是Lipschitz连续的,因此
是Lipschitz连续的,因此 在
在 上几乎处处是可导的,即存在一个勒贝格可积函数
上几乎处处是可导的,即存在一个勒贝格可积函数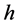 使得
使得
 。
。
函数 就是分出函数在
就是分出函数在 点的斜率,因此,
点的斜率,因此,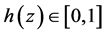 ,
,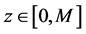 ,我们称函数
,我们称函数 是“边际赔偿函数(MIF)”。
是“边际赔偿函数(MIF)”。
经典的风险模型研究中,经常得到停止损失或比例停止损失是最优的分出风险。但是Balbas (2015) [15] 指出,在实际中再保险人很难接受这一类分出损失,因为分出风险在超过某一范围时缺少对再保险人的一些奖励性政策。因此,Balbas规定在分出损失进行一定的范围限制进而避免这种情况。
本文中根据Balbas的观点,我们建立边际赔偿函数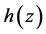 满足如下集合:
满足如下集合:
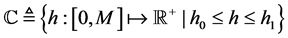 ,
,
其中 和
和 是两个常数并且满足
是两个常数并且满足 。
。
因此,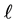 可以记为
可以记为
 。
。
2.4. 最优再保险模型
假设保险公司用失真风险度量 对总风险进行度量,使得在总风险的
对总风险进行度量,使得在总风险的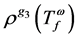 最小的情况下得到最优的分出函数
最小的情况下得到最优的分出函数 ,即考虑下面的最优化问题:
,即考虑下面的最优化问题:
 (2)
(2)
其中 ,
, 是失真函数。
是失真函数。
3. 失真风险度量下的最优再保险
对于(2)式的最优化问题,我们可以通过“边际索赔函数(MIF)”得到它的一个等价最优化标准。首先给如下引理:
引理 1 (Zhuang 2007)对任意的失真函数 ,任意的
,任意的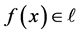 ,则存在函数
,则存在函数 使得
使得

并且
 。
。
根据引理1,可以得到 和
和 分别为:
分别为:
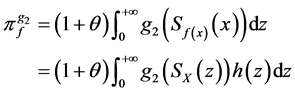 (3)
(3)
和
 。 (4)
。 (4)
因此,由(3)式和(4)式我们就能得到 的表达式为:
的表达式为:
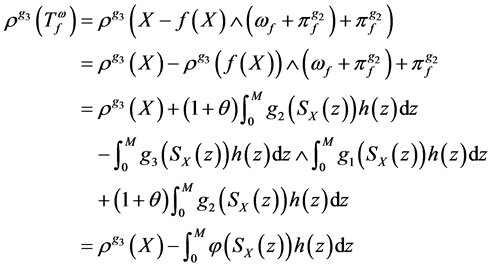
其中
 。 (5)
。 (5)
由于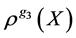 是一个常数,故只分析
是一个常数,故只分析

就能得到(2)式的最优解。因此,我们将最优化目标(2)式可以转化为MIF的形式如下:
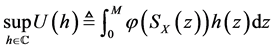 。 (6)
。 (6)
注1 假定 ,对于每一个
,对于每一个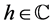 ,由于
,由于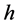 有界并且上界是
有界并且上界是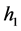 ,因此
,因此
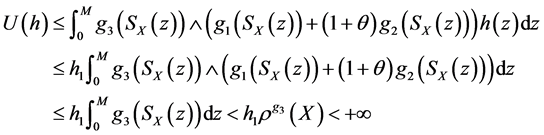
即由(2)式得到(6)式的上确界形式并且它是有界的。
根据以上的推导,我们知(6)式和(2)式的最优化目标是等价的。因此,通过对(6)式的最优化问题求解,进而可以得到(2)式的最优分出函数,具体过程及结果见定理1。这里用 表示为Lebesgue测度。
表示为Lebesgue测度。
定理1如果 是(6)式最优解当且仅当
是(6)式最优解当且仅当 表示为:
表示为:
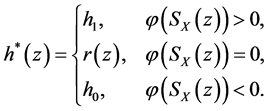 (7)
(7)
其中 的定义域是
的定义域是 。当
。当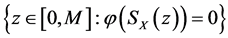 ,
,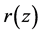 为取值在
为取值在 内的任意实值函数。
内的任意实值函数。
证明 假设存在 与
与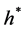 在一个Lebesgue测度集
在一个Lebesgue测度集 上是不同的,并且
上是不同的,并且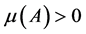 。只需证明
。只需证明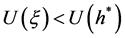 ,因此,将
,因此,将 和
和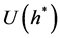 相减则有
相减则有

显然有 ,证毕。
,证毕。
注2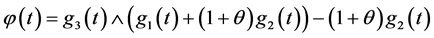 ,如果
,如果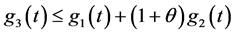 ,则
,则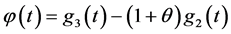 ,则定理1也是Zhuang (2015)的无保费限制的最优解。如果
,则定理1也是Zhuang (2015)的无保费限制的最优解。如果 ,则
,则 ,最优解就是考虑违约风险的最优解。
,最优解就是考虑违约风险的最优解。
由(6)式和(2)式的最优化目标的等价性。我们就能得到(2)式的最优分出损失函数为:
 (8)
(8)
其中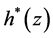 满足(7)式。如果取
满足(7)式。如果取 在
在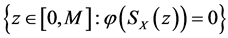 时,对应的MIF函数
时,对应的MIF函数
 。 (9)
。 (9)
是(6)式的最优解,然后就能得到(2)式的最优分出函数为
 。
。
推论1 对于(2)式的最优分出函数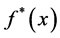 在
在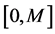 上是唯一的当且仅当
上是唯一的当且仅当
 。
。
4. 风险度量VaR和Wang’s保费原理的实例分析
在这一节,应用风险度量VaR和Wang’s保费原理来求解(2)式的最优分出函数。首先对于再保险人的准备金 ,取
,取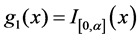 ,其中
,其中 。在保险保费为Wang’s保费原理,即
。在保险保费为Wang’s保费原理,即 ,其中
,其中 是增的凹函数且
是增的凹函数且 。对于(2)式中度量总风险的失真风险度量
。对于(2)式中度量总风险的失真风险度量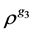 ,我们取
,我们取 ,其中
,其中 。根据以上的假设,(5)式可以具体的表示为:
。根据以上的假设,(5)式可以具体的表示为:

其中 ,
, 是增的凹函数且
是增的凹函数且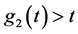 ,
, 。
。
接下来主要讨论 中
中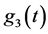 与
与 大小关系进而得到最优的分出函数。
大小关系进而得到最优的分出函数。
(a) 若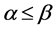 ;则
;则
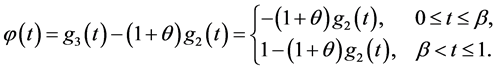 。
。
(i) 如果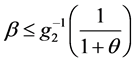
由于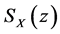 在
在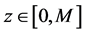 是单调递减,因此,复合函数
是单调递减,因此,复合函数 表示为:
表示为:

因此,根据定理1和(9)式,我们就能得到(6)式的最优解为:

最后根据(8)式,就能得到(2)式的最优分出函数
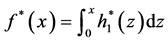 。
。
(ii) 如果 ,复合函数
,复合函数 表示为:
表示为:

因此,根据定理1和(9)式,对应(6)式的最优解为:

从而(2)式的最优分出函数为
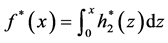 。
。
(b) 若 ;记
;记
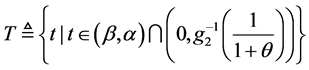 。
。
当 ,
, ;当
;当 ,
, 。
。
(i) 如果 ,则
,则 。
。
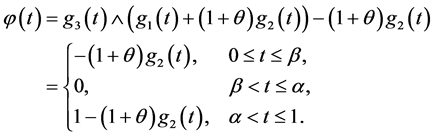
则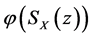 表示为:
表示为:
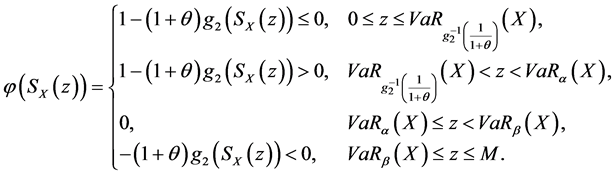
显然,根据(9)式,(6)式的最优解为:
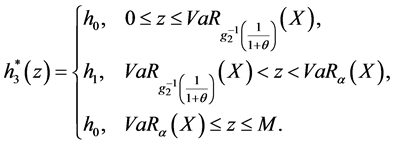
则(2)式的最优分出函数为
 。
。
(ii) 如果 ,则
,则 。
。
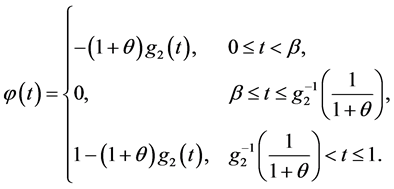
则 表示为:
表示为:
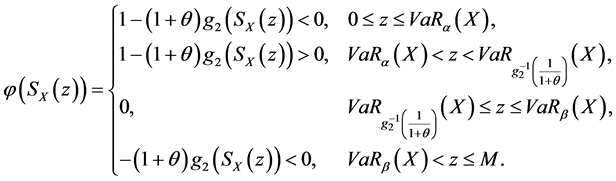
根据(9)式,(6)式的最优解为:
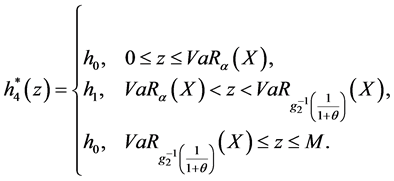
则(2)式的最优分出函数为
 。
。
(iii) 如果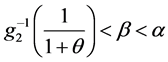 ,则
,则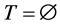 。
。

则 :
:

同样根据(9)式,得到(6)式的最优解为:

则(2)式的最优分出函数为
 。
。
5. 结论
本文考虑了再保险人的违约风险,建立了含有违约风险的再保险优化模型,为了避免再保险中的道德风险以更适应再保险市场,对分出损失进行一定范围的限制,然后应用失真风险度量和失真保费原理,通过边际索赔(MIF)函数与分出函数之间的关系建立了与之等价的再保险优化模型模型,进而得到最优分出函数的具体表达形式。最后通过具体的风险度量VaR和Wang’s保费原理得到对应的最优分出函数。传统的应用风险度量来研究最优再保险时,均是先构造一个分出函数的形式,然后来证明它是最优的。但是运用MIF函数,对最优化标准求解就能简单直观的得到最优的MIF函数,进而得到最优的分出损失。因此,应用边际赔偿(MIF)函数是我们研究最优再保险的有力工具。
基金项目
国家自然科学基金资助项目(11361058)。
文章引用
杜军红,吴黎军. 边际赔偿函数和违约风险下的最优再保险
The Optimal Reinsurance under the Marginal Indemnification Function and the Default Risk[J]. 统计学与应用, 2017, 06(02): 146-155. http://dx.doi.org/10.12677/SA.2017.62017
参考文献 (References)
- 1. Borch, K. (1960) An Attempt to Determine the Optimum Amount of Stop Loss Reinsurance. Transactions of the 16th International Congress of Actuaries, 1, 597-610.
- 2. Arrow, K.J. (1963) Uncertainty and the Welfare Economics of Medical Care. American Economic Review, 53, 941-973.
- 3. Young, V.R. (1999) Optimal Insurance under Wang’s Premium Principle. Insurance Mathe-matics and Economics, 25, 109-122. https://doi.org/10.1016/S0167-6687(99)00012-8
- 4. Kaluszka, M. (2001) Optimal Rein-surance under Mean-Variance Premium Principles. Insurance Mathematics and Economics, 28, 61-67. https://doi.org/10.1016/S0167-6687(00)00066-4
- 5. Cai, J. and Tan, K.S. (2007) Optimal Retention for a Stop-Loss Reinsur-ance under the VaR and CTE Risk Measures. Astin Bulletin, 37, 93-112. https://doi.org/10.2143/AST.37.1.2020800
- 6. Cai, J., Tan, K.S., Weng, C., et al. (2008) Optimal Reinsurance under VaR and CTE Risk Measures. Insurance: Mathematics and Economics, 43, 185-196. https://doi.org/10.1016/j.insmatheco.2008.05.011
- 7. Cheung, K.C. (2010) Optimal Reinsurance Revisited—A Geometric Approach. ASTIN Bulletin: The Journal of the IAA, 40, 221-239. https://doi.org/10.2143/AST.40.1.2049226
- 8. Chi, Y. and Tan, K.S. (2011) Optimal Reinsurance under VaR and CVaR Risk Measures: A Simplified Approach. Astin Bulletin, 41, 487-509.
- 9. Chi, Y. and Tan, K.S. (2013) Optimal Reinsurance with General Premium Principles. Insurance: Mathematics and Economics, 52, 180-189. https://doi.org/10.1016/j.insmatheco.2012.12.001
- 10. Cui, W., Yang, J. and Wu, L. (2013) Optimal Reinsurance Minimizing the Distortion Risk Measure under General Reinsurance Premium Principles. Insurance Mathematics and Economics, 53, 74-85. https://doi.org/10.1016/j.insmatheco.2013.03.007
- 11. Zheng, Y., Cui, W. and Yang, J. (2015) Optimal Reinsurance under Distortion Risk Measures and Expected Value Premium Principle for Reinsurer. Journal of Systems Science and Complexity, 28, 122-143. https://doi.org/10.1007/s11424-014-2095-z
- 12. Cai, J., Lemieux, C., Liu, F., et al. (2014) Optimal Reinsurance with Regulatory Initial Capital and Default Risk. Insurance Mathematics and Economics, 57, 13-24. https://doi.org/10.1016/j.insmatheco.2014.04.006
- 13. Assa, H. (2014) On Optimal Reinsurance Policy with Distortion Risk Measures and Premiums. SSRN Electronic Journal, 61, 70-75. https://doi.org/10.2139/ssrn.2448678
- 14. Zhuang, S.C., Weng, C., Tan, K.S., et al. (2016) Marginal Indemnification Function Formulation for Optimal Reinsurance. Insurance Mathematics and Economics, 67, 65-76. https://doi.org/10.1016/j.insmatheco.2015.12.003
- 15. Balas, A., Balbs, B., Balbs, R., et al. (2015) Op-timal Reinsurance under Risk and Uncertainty. Insurance Mathematics and Economics, 60, 61-74. https://doi.org/10.1016/j.insmatheco.2014.11.001