Advances in Applied Mathematics
Vol.04 No.01(2015), Article ID:14859,8
pages
10.12677/AAM.2015.41005
The Existence and Uniqueness of Solution for Some Kinds of Stochastic Differential Equations
Chen Chen, Yindi Zhang*, Limei Ren
College of Science, Chang’an University, Xi’an Shaanxi
Email: chdccq@163.com, *mathydzh@126.com
Received: Jan. 27th, 2015; accepted: Feb. 10th, 2015; published: Feb. 17th, 2015
Copyright © 2015 by authors and Hans Publishers Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/



ABSTRACT
Stochastic differential equation (SDE) is a relatively new discipline branch linking the deterministic and non-deterministic phenomenon [1] . The method of studying SDE is proceeded from two aspects of qualitative and quantitative. Qualitative aspect is studying the existence, uniqueness and stability of the solution of SDE; and quantitative aspect is concerning the solving method and the statistical characteristics of the solving process [2] . In order to carry out the following proof, the thesis presents some basic theory knowledge about stochastic differential equation. By means of doing transforms, we obtain the expressions solution of SDE with the help of the formula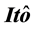 , and thus we show the existence of the SDE. And finally, we prove the uniqueness of the solution of the SDE by utilizing the Cauchy-Schwarz inequality, the Lipschitz condition and the Gronwall’s lemma.
, and thus we show the existence of the SDE. And finally, we prove the uniqueness of the solution of the SDE by utilizing the Cauchy-Schwarz inequality, the Lipschitz condition and the Gronwall’s lemma.
Keywords:Stochastic Differential Equation, Existence and Uniqueness, Cauchy-Schwarz Inequality, Lipschitz Conditions, Gronwall’s Lemma

几种随机微分方程解的存在性与唯一性
陈晨,张引娣*,任丽梅
长安大学,理学院,陕西 西安
Email: chdccq@163.com, *mathydzh@126.com
收稿日期:2015年1月27日;录用日期:2015年2月10日;发布日期:2015年2月17日

摘 要
随机微分方程是把确定性现象和非确定性现象联系起来的一门比较新兴的学科分支[1] 。研究随机微分方程的方法是从定性和定量两方面进行的,定性方面是研究解的存在性、唯一性和稳定性;而定量方面是研究求解的方法及求解过程的统计特性[2] 。此篇论文首先介绍了随机微分方程的一些基本理论知识,对几种具体的随机微分方程做了一些定性的探讨,证明了几种随机微分方程解的存在性与唯一性。解的存在性的证明方法是先作变换,再借助伊藤公式,推导出解的表达式,从而也就证明了解的存在性。而解的唯一性证明过程中运用了Cauchy-Schwarz不等式和Lipschitz条件,还用到了Gronwall引理。
关键词 :随机微分方程,存在唯一性,Cauchy-Schwarz不等式,Lipschitz条件,Gronwall引理

1. 引言
随机微分方程是20世纪中叶发展起来的一个较新学科分支。系数为随机量的常微分方程和由随机过程驱动的微分系统,一般称为随机微分方程。又因为前者可以直接地处理为随机参数的常微分方程,所以通常的随机微分方程常常专门指后者。随机微分方程的概念最早以布朗运动的形式,由Einstein在他的那篇著名的论文中提出。这个方向的研究工作随后由Langevin等继续研究,此后伊藤清和Stratonovich [3] 完善了随机微分方程的数学基础,使得这门学科更加科学严谨。随机微分方程多用于对一些多样化现象进行建模,比如不停变动的股票价格,部分物理现象如热扰动等。随机微分方程在数学以外的许多领域有着广泛的应用,它对数学领域中的许多分支起着有效的联结作用。近年来,在一些新兴的科学技术领域中大量出现随机微分方程的问题,如在随机干扰下的控制问题,通信技术中的滤波问题,生物数学模型的建立问题和随机振动问题等,都依赖于随机微分方程的研究和解决。
2. 预备知识
2.1. 伊藤 公式
公式
设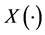 满足随机微分方程
满足随机微分方程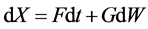 ,其中
,其中 ,
,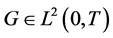 。假定
。假定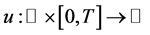 是连续的,且具有连续偏导数
是连续的,且具有连续偏导数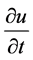 ,
, ,
, 令。
令。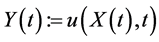 那么
那么 有如下的伊藤微分形式。
有如下的伊藤微分形式。
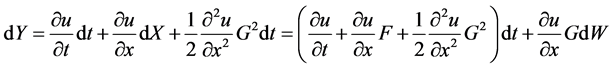 (1)
(1)
因此伊藤微分形式(1)就称为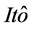 公式。
公式。
2.2. 定义
我们称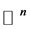 值随机过程
值随机过程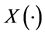 是
是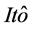 随机微分方程
随机微分方程
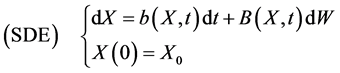
的一个解,其中 ,满足:
,满足:
(i) 对于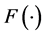 ,
,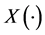 是有序可测的,
是有序可测的,
(ii) ,
,
(iii)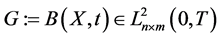 ,
,
(iv)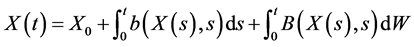 几乎必然对于所有的
几乎必然对于所有的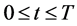 。
。
2.2.1. 注
(i) 设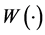 是一个
是一个 维的布朗运动,
维的布朗运动, 是一个与
是一个与 相互独立的
相互独立的 维随机变量。今后记
维随机变量。今后记
 它是由
它是由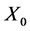 产生的
产生的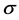 -代数,是时间
-代数,是时间 (包含
(包含 )之前的维纳过程的历史。
)之前的维纳过程的历史。
(ii) 假设给定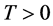 ,且
,且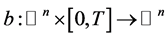
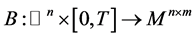
是给定的函数。(注:这些不是随机变量。)我们来具体表示这些函数,即
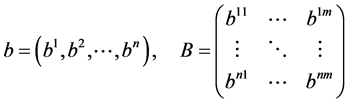
2.2.2. 注
① 如果一个高阶随机微分方程 的形式为
的形式为
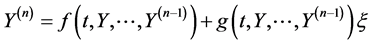
通常这里的 表示“白噪声”,上面的形式可写成
表示“白噪声”,上面的形式可写成
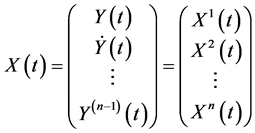
那么
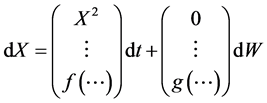
② 考虑到定义中的(iii),我们可以总是假定 几乎必然有连续的样本路径。
几乎必然有连续的样本路径。
2.3. Gronwall引理
设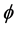 和
和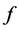 是定义在
是定义在 上的非负连续函数,其中
上的非负连续函数,其中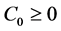 表示常数。如果
表示常数。如果
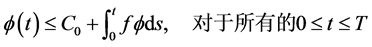 (2)
(2)
那么
 ,对于所有的
,对于所有的 。
。
2.4. 存在性与唯一性定理
假定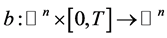 ,和
,和 ,是连续的,并且满足下面的条件[4] :
,是连续的,并且满足下面的条件[4] :
(i) (Lipschitz条件)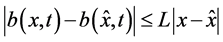 ,对于所有的
,对于所有的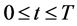 ,
,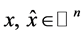 (3)
(3)
(ii) (线性增长有界条件) ,对于所有的
,对于所有的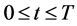 ,
,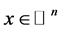 (4)
(4)
上面的条件(i)和(ii)均是对于一些常数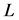 。
。
设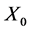 是任意
是任意 值随机变量,如果
值随机变量,如果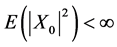 ,并且
,并且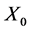 与
与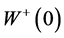 是独立的,这里的
是独立的,这里的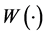 是一个给定的
是一个给定的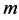 维布朗运动。
维布朗运动。
那么对于随机微分方程
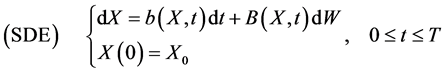
存在一个唯一解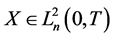 。
。
且解的表达式[5] 为
 . (5)
. (5)
文献[6] 中给出了这一定理的证明,先证唯一性,再证存在性。但是存在性的证明过程中需要构造迭代格式,并且运用了鞅不等式[7] ,切比雪夫不等式,Borel-Cantelli引理[8] ,还用到了无穷级数一致收敛,归纳法以及递推的方法,证明既繁琐又复杂。下面我们对一些具体的随机微分方程,利用Cauchy-Schwarz不等式,通过变换利用伊藤公式[9] ,再利用Gronwall引理来完成随机微分方程存在性与唯一性的证明,对于这些具体的随机微分方程证明过程变得比较简炼,使我们更容易理解接受。
注
① “唯一性”是指,如果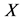 ,
, ,并且都是随机微分方程的解,且有几乎必然连续样本路径,那么
,并且都是随机微分方程的解,且有几乎必然连续样本路径,那么
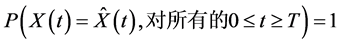
② 假设(i)是说对于变量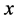 ,
, 和
和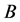 是一致Lipschitz连续的。同时注意到,假设(ii)实际可由假设(i)得到。
是一致Lipschitz连续的。同时注意到,假设(ii)实际可由假设(i)得到。
3. 几种随机微分方程解的存在唯一性
下面我们就几种不同类型的随机微分方程给出解的存在性、唯一性的证明.
3.1. 常系数的线性随机微分方程
定理2.1:布朗粒子模型的移动,一维情况的摩擦力是: ,这里的
,这里的 是“白噪声”,
是“白噪声”, 是粒子的摩擦系数,
是粒子的摩擦系数, 是扩散系数,我们可以解释
是扩散系数,我们可以解释 是布朗粒子的速率,因此我们可以将上面的式子表示成如下的随机微分方程
是布朗粒子的速率,因此我们可以将上面的式子表示成如下的随机微分方程

其中初始分布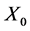 是独立的布朗运动。其中有
是独立的布朗运动。其中有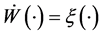 。这是郎之万方程。对此随机微分方程,可证明
。这是郎之万方程。对此随机微分方程,可证明
其解是存在唯一的,且有表达式: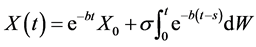 ,
,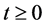
注: 是扩散系数,其具体表达式为:
是扩散系数,其具体表达式为: ,其中
,其中 是玻尔兹曼常数[10] ,
是玻尔兹曼常数[10] , 是环境温度。而玻尔兹曼常数
是环境温度。而玻尔兹曼常数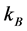 是有关温度及能量的一个物理常数,而且
是有关温度及能量的一个物理常数,而且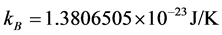 。
。
证明:先证唯一性。令 和
和 是定义在同一概率空间上具有相同初值
是定义在同一概率空间上具有相同初值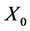 的两个解,则由解的表达式(5),得到以下两个方程:
的两个解,则由解的表达式(5),得到以下两个方程:
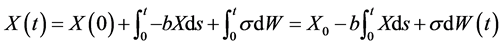
和
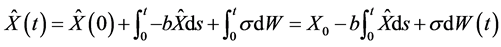
其中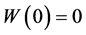 .
.
两式相减得出

由 不等式,有
不等式,有

令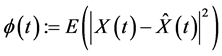 ,则
,则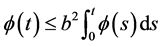 ,由Gronwall引理中的(2)式,知:
,由Gronwall引理中的(2)式,知: ,且
,且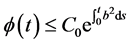 ,故
,故 ,即
,即 ,则
,则 与
与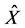 无区别,唯一性得证。
无区别,唯一性得证。
再证存在性。令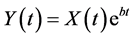 ,且
,且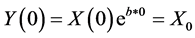 。
。
根据伊藤公式(1),知
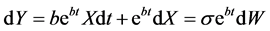
两边同时积分,得出

故 ,
, 。因此其解存在,存在性得证。
。因此其解存在,存在性得证。
3.2. 简单的线性齐次随机微分方程
定理2.2:假设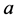 和
和 均是常数。满足
均是常数。满足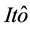 随机微分方程
随机微分方程
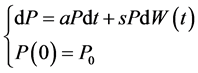
则此随机微分方程的解是存在唯一的,并且其唯一解的表达式是:
 ,其中
,其中
证明:先证唯一性。令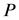 和
和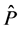 是定义在同一概率空间上具有相同初值
是定义在同一概率空间上具有相同初值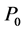 的两个解,则由解的表达式(5),得到以下两个方程:
的两个解,则由解的表达式(5),得到以下两个方程:
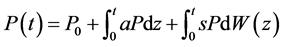
和
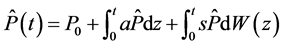
两式相减,可以得出对于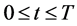 ,有
,有

因为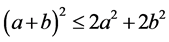 ,所以
,所以

由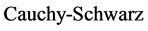 不等式,有
不等式,有
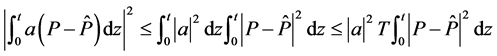
则
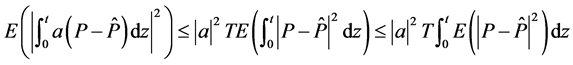
由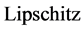 条件(3)式知,存在
条件(3)式知,存在 使得
使得
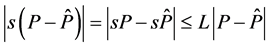
其中 。
。
进而有

其中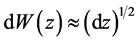 。
。
故
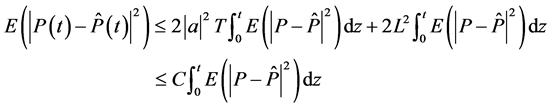
其中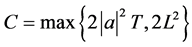 为一些常数。
为一些常数。
令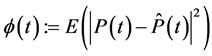 ,则有
,则有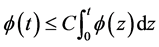 ,由Gronwall引理中的(2)式,知:
,由Gronwall引理中的(2)式,知: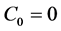 ,且
,且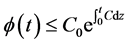 ,因而
,因而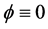 ,即
,即
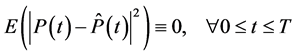
因而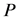 和
和 无区别,唯一性得证。
无区别,唯一性得证。
再证存在性。令 ,且
,且 。
。
利用伊藤公式(1),知
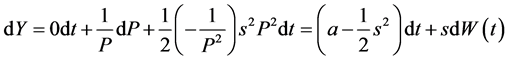
两边同时积分得
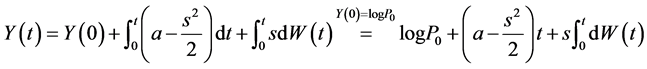
所以

故其解存在,存在性得证。
3.3. 一般的线性非齐次随机微分方程
3.3.1. 其一般形式
设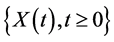 满足
满足
其中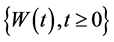 是一维标准布朗运动,
是一维标准布朗运动,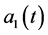 ,
,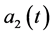 ,
, ,
,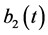 是
是 的一般函数(也可以是常数)。设它们在
的一般函数(也可以是常数)。设它们在 上波雷尔可测[3] (容易验证,单调函数,逐段单调函数及连续函数均是博雷尔可测函数)且有界,设
上波雷尔可测[3] (容易验证,单调函数,逐段单调函数及连续函数均是博雷尔可测函数)且有界,设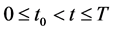 ,初始值
,初始值 关于
关于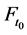 可测。
可测。
3.3.2. 一个特殊的多元伊藤公式
设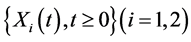 满足
满足

令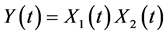 ,则
,则
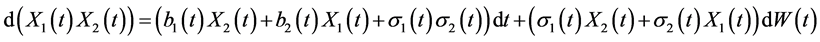 (6)
(6)
下面对一般的线性非齐次随机微分方程,我们先推导出它所对应的齐次方程的基本解,进而再给出线性非齐次随机微分方程一般解的表达式。
定理2.3:设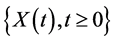 满足伊藤方程
满足伊藤方程
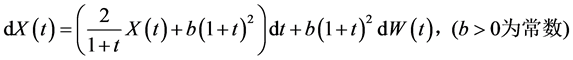
则对应的齐次线性方程的基本解为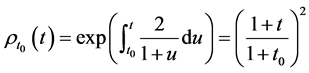 ,而非齐次随机微分方程的一般解为
,而非齐次随机微分方程的一般解为

证明:令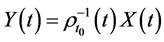 ,且
,且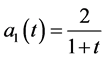 ,
,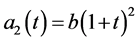 ,
,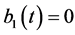 ,
,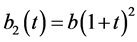
而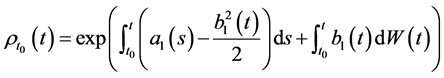 ,则
,则

即
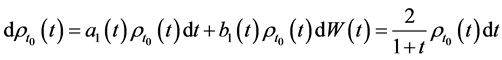
而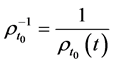 ,则由伊藤公式⑴可得
,则由伊藤公式⑴可得
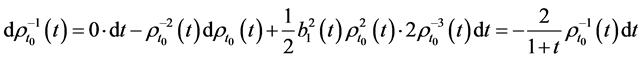
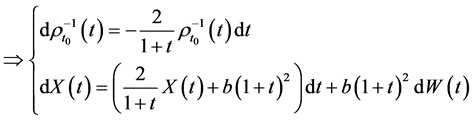
则由(6)式得
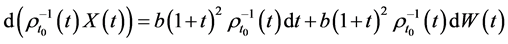 ,
,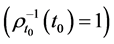 两边同时积分,得
两边同时积分,得
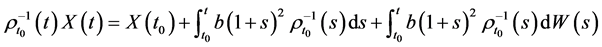
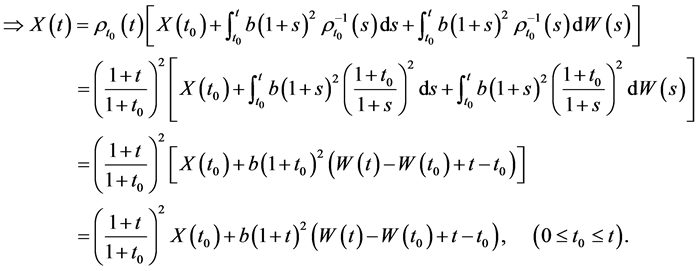
4. 结束语
这篇论文通过对一些具体的随机微分方程进行探讨,证明了其解的存在性与唯一性,其中主要利用Cauchy-Schwarz不等式来证明这些具体的线性随机微分方程解唯一性,而存在性的证明通过作变换并利用伊藤公式,推导出几种随机微分方程解的具体表达式,从而完成了存在性的证明。从证明过程可以看出Lipschitz条件必不可少。我们给出的证明方法简单明了,这对于初次涉入这一领域的人会有一定的启发作用。希望有兴趣的老师同学与我们共勉,使我们能更多地深入了解到这方面的知识以及它的广泛应用。
基金项目
国家自然科学基金11401044(NSFC No. 11401044)。
文章引用
陈晨,张引娣,任丽梅, (2015) 几种随机微分方程解的存在性与唯一性
The Existence and Uniqueness of Solution for Some Kinds of Stochastic Differential Equations. 应用数学进展,01,37-45. doi: 10.12677/AAM.2015.41005
参考文献 (References)
- 1. 孙清华, 孙昊 (2004) 随机过程内容、方法与技巧. 华中科技大学出版社, 武汉, 206-216.
- 2. 田铮, 秦超英 (2007) 随机过程与应用. 科学出版社, 北京, 97-100.
- 3. 刘嘉焜, 王公恕 (2001) 应用随机过程(第二版). 科学出版社, 北京, 218-238.
- 4. 林元烈 (2001) 应用随机过程. 清华大学出版社, 北京, 288-312.
- 5. 李顺萍 (2010) 随机微分方程样本广义解. 硕士论文, 华中科技大学, 王湘君.
- 6. Evans, L.C. (1999) An introduction to stochastic differential equations (Version 1.2). Department of Mathematics University of California, Berkeley, 81-95.
- 7. Gillespie, I.I. and Skorohod, A.V. (1972) Stochastic differential equations. Springer, Berlin.
- 8. Arnold, L. (1974) Stochastic differential equations: Theory and applications. Wiley, Hoboken.
- 9. 王子亭, 李萍 (2009) 分类随机微分方程的一般解. 中国石油大学学报: 自然科学版, 1, 167-170.
- 10. 金治明 (1985) 一类随机微分方程的解法. 湖南数学年刊, 1, 1-8.