Advances in Applied Mathematics
Vol.04 No.03(2015), Article ID:15892,16 pages
10.12677/AAM.2015.43031
Combinatorial and Geometric Proofs of the Number of Triangles with Integer Sides
Yajing Cai1, Zhengli Tan1, Fugang Chao1, Han Ren1,2
1Mathematics Department, East China Normal University, Shanghai
2Shanghai Key Laboratory of Pure Mathematics and Mathematical Practice, Shanghai
Email: chaofugang@126.com
Received: Jul. 28th, 2015; accepted: Aug. 12th, 2015; published: Aug. 18th, 2015
Copyright © 2015 by authors and Hans Publishers Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/



ABSTRACT
Integer partitions refer to a representation of the positive integer n as a sum
of integers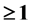 . We
do not consider the order of terms of the sum. The problem of counting non-congruent
triangles with integer sides is just a case of partition of integers. Now, there
have been many results about the study of triangles with integer sides problem.
In this article, we will solve the problem in two ways. Firstly, we take the common
version using the theory of integer partitions to give a proof. Here, we will require
generating functions. By using Ferrers diagram, the integer triangles problem will
cross to the solution with integers
. We
do not consider the order of terms of the sum. The problem of counting non-congruent
triangles with integer sides is just a case of partition of integers. Now, there
have been many results about the study of triangles with integer sides problem.
In this article, we will solve the problem in two ways. Firstly, we take the common
version using the theory of integer partitions to give a proof. Here, we will require
generating functions. By using Ferrers diagram, the integer triangles problem will
cross to the solution with integers
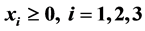 of
of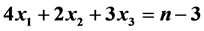 , while the
sum of
, while the
sum of
 is equal to the solution of triangles with integer sides problem using the method
of generating function. Secondly, we give a geometric approach using triangular
coordinates which is easier to understand. Since
is equal to the solution of triangles with integer sides problem using the method
of generating function. Secondly, we give a geometric approach using triangular
coordinates which is easier to understand. Since ,
we can view
,
we can view
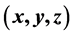 as a point in the space
as a point in the space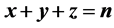 ,
in the triangle cutting off by the planes
,
in the triangle cutting off by the planes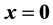 ,
,
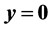 ,
, .
Then, the sum of the integral values of
.
Then, the sum of the integral values of
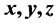 corresponds to the number of non-congruent triangles with integer sides. Also, we
bring out several further properties, including the number of non-congruent triangles
types, such as Isosceles triangles and Equilateral triangles. At the end, we study
more about right triangles, acute triangles and obtuse triangles in the non-congruent
triangles. But we can just get some relevant properties and conjectures now.
corresponds to the number of non-congruent triangles with integer sides. Also, we
bring out several further properties, including the number of non-congruent triangles
types, such as Isosceles triangles and Equilateral triangles. At the end, we study
more about right triangles, acute triangles and obtuse triangles in the non-congruent
triangles. But we can just get some relevant properties and conjectures now.
Keywords:Partition of Integers, Ferrers Diagram, Geometric Approach, Triangle Types

整数边三角形个数的组合与几何证明方法
蔡雅静1,镡镇鹂1,晁福刚1,任韩1,2
1华东师范大学数学系,上海
2上海市核心数学与实践重点实验室,上海
Email: chaofugang@126.com
收稿日期:2015年7月28日;录用日期:2015年8月12日;发布日期:2015年8月18日

摘 要
整数分拆是指将正整数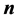 表示成一些正整数的无序和。周长为
表示成一些正整数的无序和。周长为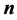 的整数边不全等三角形个数问题是整数分拆里的一个特殊情况。目前对于整数边三角形问题的研究已有许多结果。本文将采用两种方法证明整数边三角形个数的表达式。方法一采用组合学上整数分拆的方法,方法二是运用空间格点方法证明。在方法一中介绍了整数分拆理论求解的常规方法,利用Ferrers图把整数边三角形个数问题求解转化为
的整数边不全等三角形个数问题是整数分拆里的一个特殊情况。目前对于整数边三角形问题的研究已有许多结果。本文将采用两种方法证明整数边三角形个数的表达式。方法一采用组合学上整数分拆的方法,方法二是运用空间格点方法证明。在方法一中介绍了整数分拆理论求解的常规方法,利用Ferrers图把整数边三角形个数问题求解转化为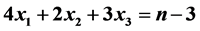 的非负整数解个数求解,继而可采用生成函数法求解
的非负整数解个数求解,继而可采用生成函数法求解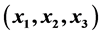 的个数,也即原问题中周长为
的个数,也即原问题中周长为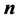 的不全等整数边三角形的个数。在方法二中,借助于几何方法,把原问题中三角形三边
的不全等整数边三角形的个数。在方法二中,借助于几何方法,把原问题中三角形三边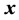 、
、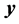 、
、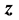 所需满足的条件:
所需满足的条件: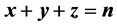 且
且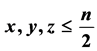 转化为三维坐标轴中对应的平面图,因为
转化为三维坐标轴中对应的平面图,因为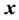 、
、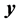 、
、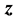 为整数,所以实则对应于一网格点图,通过研究网格点的性质可求出整数边三角形的个数表达式。此外,本文还进一步研究了三角形的各类型个数与其间关系。例如,其中包含的等腰、等边三角形的个数表达式。对于直角、锐角、钝角三角形个数问题,目前只得出相关性质的一些结论和猜想。
为整数,所以实则对应于一网格点图,通过研究网格点的性质可求出整数边三角形的个数表达式。此外,本文还进一步研究了三角形的各类型个数与其间关系。例如,其中包含的等腰、等边三角形的个数表达式。对于直角、锐角、钝角三角形个数问题,目前只得出相关性质的一些结论和猜想。
关键词 :整数分拆,Ferrers图,数形结合,三角形类型

1. 引言
(1) 问题提出
本文需要证明如下问题:具有整数边长且周长为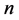 的不全等三角形的个数等于
的不全等三角形的个数等于
 。这里,
。这里,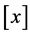 表示实数
表示实数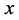 的取整函数。
的取整函数。
(2) 背景介绍
给定周长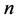 ,能构成的不全等的整数边三角形有多少个?这个问题来自于Louis
Comtet的“Advanced Combinatorics”一书,书中直接给出了一个表达式(文献[1] )。这个问题是整数分拆理论中的一个特殊情况,即把整数
,能构成的不全等的整数边三角形有多少个?这个问题来自于Louis
Comtet的“Advanced Combinatorics”一书,书中直接给出了一个表达式(文献[1] )。这个问题是整数分拆理论中的一个特殊情况,即把整数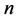 划分为三部分,分别作为三角形的三边边长,并需要满足能构成三角形的相关条件。在1674年,Leibniz首先提出分拆这个概念(文献[2]
),例如,3可以分拆成1 + 2或1 + 1 + 1,也可以是3它本身,所以3的无序分拆数为3。那么对于一般情况,
划分为三部分,分别作为三角形的三边边长,并需要满足能构成三角形的相关条件。在1674年,Leibniz首先提出分拆这个概念(文献[2]
),例如,3可以分拆成1 + 2或1 + 1 + 1,也可以是3它本身,所以3的无序分拆数为3。那么对于一般情况, 的分拆为一些无序正整数之和的个数为多少呢?后来,整数分拆理论就发展起来了。设
的分拆为一些无序正整数之和的个数为多少呢?后来,整数分拆理论就发展起来了。设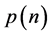 为
为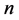 表示成无序正整数之和的总个数,例如,p(3)=3。那么,能给出
表示成无序正整数之和的总个数,例如,p(3)=3。那么,能给出 确定的计算方法和表达式么?在Euler
(文献[3] ),Rogers (文献[4] ),Ramanujan (文献[5] ),Hardy (文献[6] ),MacMahon (文献[7] ),Rademacher
(文献[8] ) and Sylvester (文献[9] )的努力下,现已有一套比较完善的整数分拆理论,文献[8] 中得到
确定的计算方法和表达式么?在Euler
(文献[3] ),Rogers (文献[4] ),Ramanujan (文献[5] ),Hardy (文献[6] ),MacMahon (文献[7] ),Rademacher
(文献[8] ) and Sylvester (文献[9] )的努力下,现已有一套比较完善的整数分拆理论,文献[8] 中得到 的一个估计式。
的一个估计式。
(3) 本文概述
对于本论文所要研究的问题,即整数分拆的一个特殊情况—整数边三角形个数问题,我们将在正文前部的方法一中将给出运用组合学中整数分拆理论的方法,其中需用到Ferrers图把原问题转化为我们
熟知的问题,再运用生成函数法来解得结果。该问题的生成函数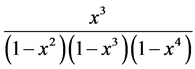 的系数序列已被命名为Alcuin’s
Sequence (详见文献[10] )。
的系数序列已被命名为Alcuin’s
Sequence (详见文献[10] )。
是否还能从其他角度来解这个问题?这儿,我们运用组合几何(文献[11] )上的空间格点方法,给出了从另一角度证明的方案。除此之外,我们是否还可以进一步细致研究一下三角形的各类型的个数?为此,我们通过空间网格图形中格点的性质,得出了特殊三角形—等腰、等边三角形的个数表达式。在研究直角、钝角、锐角三角形时,目前只能得出一些性质和相关猜想,其个数问题还有待进一步研究。
2. 主要结果
2.1. 组合方法证明
周长为 的整数边三角形个数问题,我们可从三角形的三边着手讨论。三角形的三边边长满足和为定值
的整数边三角形个数问题,我们可从三角形的三边着手讨论。三角形的三边边长满足和为定值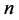 ,类似于整数分拆里的
,类似于整数分拆里的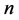 的三分拆情形,但多了约束条件,即这分拆的三部分需满足构成三角形的一些条件。
的三分拆情形,但多了约束条件,即这分拆的三部分需满足构成三角形的一些条件。
下面,我们先引入整数分拆的概念(文献[12] )。
设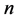 为任一正整数。整数分拆是指,对于取定的
为任一正整数。整数分拆是指,对于取定的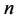 ,表示成一些正整数之和,这些正整数称为
,表示成一些正整数之和,这些正整数称为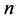 的分拆项,不考虑次序。例如,对于正整数5的分拆如下:5
= 5;5 = 1 + 4;5 = 2 + 3;5 = 1 + 1 + 3;5 = 1 + 2 + 2;5 = 1 + 1 + 1 + 2;5 = 1 + 1
+ 1 + 1 + 1。这里为了避免在不考虑次序前提下分拆出现重复,故把分拆项由小到大相加表示。
的分拆项,不考虑次序。例如,对于正整数5的分拆如下:5
= 5;5 = 1 + 4;5 = 2 + 3;5 = 1 + 1 + 3;5 = 1 + 2 + 2;5 = 1 + 1 + 1 + 2;5 = 1 + 1
+ 1 + 1 + 1。这里为了避免在不考虑次序前提下分拆出现重复,故把分拆项由小到大相加表示。
原问题中三角形个数问题是 的三分拆的特殊情形。故在此,我们先给出
的三分拆的特殊情形。故在此,我们先给出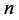 的
的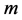 分拆(
分拆(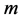 为正整数)的定义。
为正整数)的定义。
定义2.1:正整数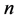 的分成
的分成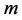 (
(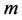 为正整数)个被加数的分拆可以看成是方程:
为正整数)个被加数的分拆可以看成是方程: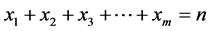 ,
,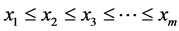 ,
,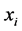 为正整数,
为正整数,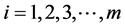 ,的解。方程解
,的解。方程解 的集合称为
的集合称为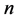 的
的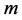 分拆。对任一解
分拆。对任一解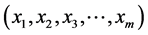 ,则称为
,则称为 的
的 分拆项。
分拆项。
下面的定理是明显的。
定理2.1:任意给定正整数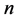 的一个分拆,则对应于方程
的一个分拆,则对应于方程 的一个解,解
的一个解,解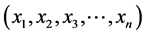 中
中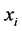 则对应该分拆中分拆数
则对应该分拆中分拆数 的个数。
的个数。
由以上定理中方程的形式,我们可以知道,在求解的个数时,可采用生成函数法。因此,我们需要把三角形问题转化为类似上述定理中的式子。而这一转化过程需借助Ferrers图来完成。为此,我们先引入Ferrers图(文献[13] )的定义。
定义2.2:对于正整数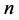 的任一分拆(如上定义),对应于一组
的任一分拆(如上定义),对应于一组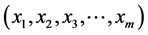 ,不妨设
,不妨设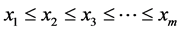 ,其中
,其中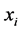 为正整数,
为正整数,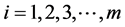 ,我们把
,我们把 用对应个数的间隔相等的横向小圆点列表示,则
用对应个数的间隔相等的横向小圆点列表示,则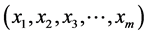 可表示成
可表示成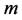 组小圆点列,可将它们从上到下依次靠左对齐排列,所产生的图则称为Ferrers图。
组小圆点列,可将它们从上到下依次靠左对齐排列,所产生的图则称为Ferrers图。
例如,18的一个分拆,18 = 1 + 2 + 2 + 4 + 4 + 5,对应的Ferrers图如图1所示。
易见,Ferrers图可以唯一确定正整数 的一个分拆。
的一个分拆。
在介绍了整数分拆的概念以及其简单性质,和Ferrers图的定义后,下面我们将借助上述内容分析一下整数边三角形个数问题。
问题重述:求证具有整数边长且周长为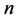 的不全等三角形的个数的表达式为
的不全等三角形的个数的表达式为 。
。
这里,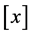 表示实数
表示实数 的取整函数。
的取整函数。
证明过程如下:
假设周长为 的整数边三角形三边长为
的整数边三角形三边长为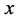 ,
, ,
,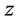 ,那么需满足:
,那么需满足: ,
,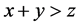 ,
,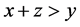 ,
,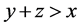 ,
,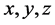 为正整数。不妨设
为正整数。不妨设 。取满足上述条件的任意一组解
。取满足上述条件的任意一组解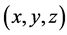 ,其对应的Ferrers图如下图2所示:
,其对应的Ferrers图如下图2所示:
在上图所示的右边图中,表示的是Ferrers图顺时针旋转90度后所得的图。在图2的右图中,令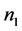 表示一个点的行数,
表示一个点的行数,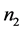 表示两个点的行数,
表示两个点的行数,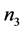 表示三个点的行数。那么有:
表示三个点的行数。那么有: 。
。
由条件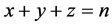 ,
,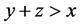 ,
,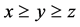 可等价为关于
可等价为关于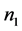 ,
,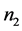 ,
, 的下列式子:
的下列式子: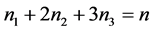 ,
, ,
,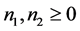 。
。
整理上述式子可得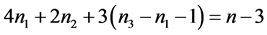 ,
, ,
, ,
, 。
。
令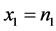 ,
,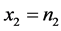 ,
,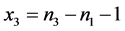 ,则上述条件转化为
,则上述条件转化为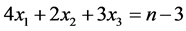 ,
,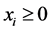 ,
,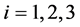 。
。
由上述推导过程可知,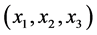 与
与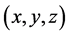 一一对应。所以,至此,原来的不全等整数边三角形个数问题转化为
一一对应。所以,至此,原来的不全等整数边三角形个数问题转化为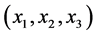 解的个数问题。解一般的不定方程是困难的,在这里我们通过一个简单的线性变换,将问题转化为已经解决的不定方程的解的问题。
解的个数问题。解一般的不定方程是困难的,在这里我们通过一个简单的线性变换,将问题转化为已经解决的不定方程的解的问题。
对于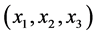 需满足条件
需满足条件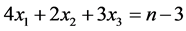 ,
,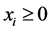 ,
,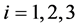 的求解,即采用生成函数法。对
的求解,即采用生成函数法。对

Figure 1. Partition of 18
图1. 18的分拆
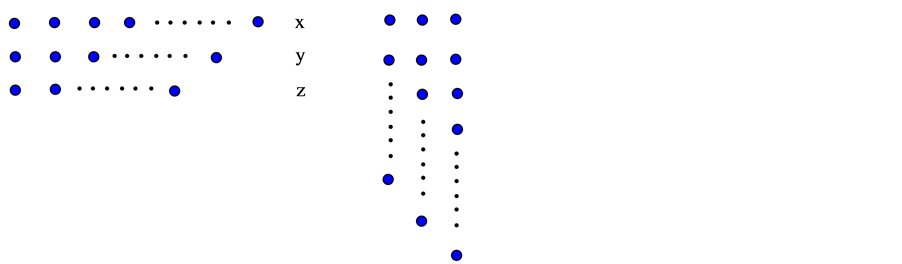
Figure 2. 3-partition of n
图2. n的3分拆
应的生成函数如下:
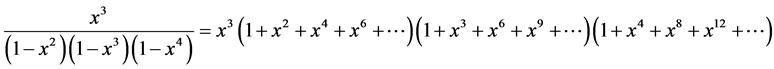 (1)
(1)
由生成函数法理论可知,上面(1)式的展开式中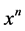 前面的系数即为方程
前面的系数即为方程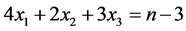 的解
的解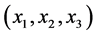 的个数(文献[13]
),也即原问题中周长为
的个数(文献[13]
),也即原问题中周长为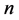 的不全等整数边三角形的个数。
的不全等整数边三角形的个数。
在Maple中输入命令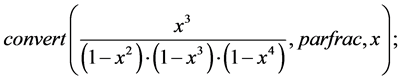 并运行,则得到(1)式的部分分式展开式为
并运行,则得到(1)式的部分分式展开式为
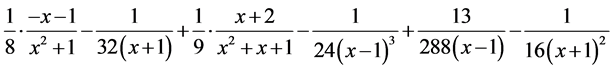 (2)
(2)
下面计算(2)式中每一项的幂级数展开式,找出 项前面的系数。
项前面的系数。
第一项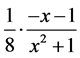 展开式中
展开式中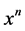 项前面的系数为
项前面的系数为 ;
;
第二项 展开式中
展开式中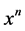 项前面的系数为
项前面的系数为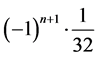 ;
;
第三项 展开式为
展开式为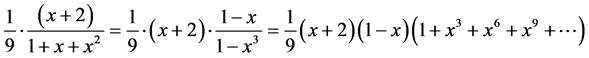 ,则
,则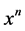 项前面的系数为
项前面的系数为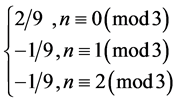 ;
;
第四项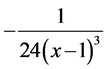 展开式中
展开式中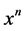 项前面的系数为
项前面的系数为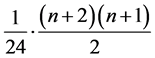 ;
;
第五项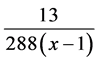 展开式中
展开式中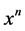 项前面的系数为
项前面的系数为 ;
;
第六项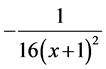 展开式中
展开式中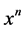 项前面的系数为
项前面的系数为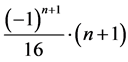 。
。
将上面所求六项的每个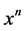 项前面的系数相加所得的和即为(1)式的幂级数展开式中
项前面的系数相加所得的和即为(1)式的幂级数展开式中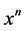 项的系数。
项的系数。
因为上面的计算结果中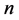 分在
分在 和
和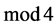 下表达式不同,所以以上结果可写成在
下表达式不同,所以以上结果可写成在 下的十二种情况下不同等式,可通过计算验证这12个等式可等价于证明题题目中的结果
下的十二种情况下不同等式,可通过计算验证这12个等式可等价于证明题题目中的结果 ,这里,
,这里,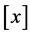 表示实数
表示实数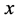 的取整函数。
的取整函数。
综上所述,我们通过分析整数边不全等三角形所要满足的条件,结合整数分拆理论和Ferrers图,将它转化为运用我们熟悉的生成函数法来求解,得到最终题目中需要证明的结果。
2.2. 空间格点方法证明
在上述第二大部分,我们把三角形问题看作整数分拆的一个特殊情形来考虑,故采用整数分拆理论和Ferrers图来解该问题。其优点在于有效地运用了现有的整数分拆理论,当然,中间还需借助Ferrers图工具,才能转化成我们熟知的形式并利用生成函数法求解。那么,是否有其他更直接、更简单易懂的方法呢?
考虑三角形的三边,把它看作三个未知数,满足和为定值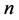 ,即满足方程
,即满足方程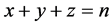 ,该方程在三维坐标轴中对应于一平面。这里研究的整数边三角形的三边是正整数,所以实则这三边对应于一平面网格点图。故下面我们将通过研究网格点图上点的性质来求解周长为
,该方程在三维坐标轴中对应于一平面。这里研究的整数边三角形的三边是正整数,所以实则这三边对应于一平面网格点图。故下面我们将通过研究网格点图上点的性质来求解周长为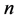 的不全等整数边三角形个数问题。
的不全等整数边三角形个数问题。
如果设一个整数边三角形的三边长分别为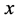 、
、 、
、 ,那么正整数
,那么正整数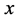 、
、 、
、 需要满足的条件为:
需要满足的条件为: 。(这里考虑了退化的三角形在内)
。(这里考虑了退化的三角形在内)
如果给定三角形周长为 ,即
,即 ,那么由上面约束条件,等价于:
,那么由上面约束条件,等价于:
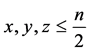 (3)
(3)
建立一个三维坐标系,画出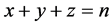 的图像,如图3所示。
的图像,如图3所示。
那么,图中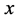 、
、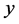 、
、 可分别对应所要研究的三角形的三边边长。因为周长为
可分别对应所要研究的三角形的三边边长。因为周长为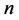 的整数边三角形需满足
的整数边三角形需满足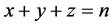 ,且
,且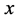 、
、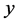 、
、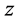 均为非负整数,所以以上条件在三维坐标轴中呈现出的平面图为网格状三角形,每个网格点即表示满足条件的整数点坐标
均为非负整数,所以以上条件在三维坐标轴中呈现出的平面图为网格状三角形,每个网格点即表示满足条件的整数点坐标 。
。
例:图4中左图为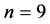 时
时 对应的网格点平面图,其中三条虚线分别对应:
对应的网格点平面图,其中三条虚线分别对应: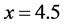 ,
,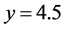 ,
, ,这三条虚线即为上述等价约束条件(3)的边界线,并构成一个等边三角形。右图为
,这三条虚线即为上述等价约束条件(3)的边界线,并构成一个等边三角形。右图为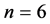 时
时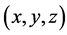 对应的网格点平面图,三条虚线分别对应
对应的网格点平面图,三条虚线分别对应 ,
,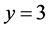 ,
, ,也构成一个等边三角形。
,也构成一个等边三角形。
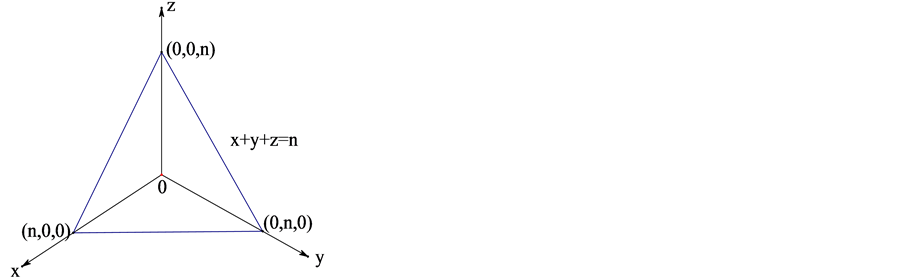
Figure 3. Function
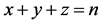
图3. 函数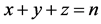

Figure 4. Lattice point graph
图4. 格点图
如上介绍了平面网格点图后,我们将研究这些网格点的性质,以便用来计算三角形的个数。这里,我们先引入一些记号以及与之相关的简单结果。
若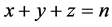 ,则记它如上所述对应的网格状三角形为
,则记它如上所述对应的网格状三角形为 。那么其上有
。那么其上有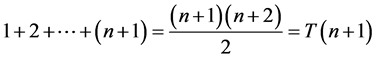 个网格点,即有
个网格点,即有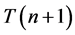 个非负整数坐标点
个非负整数坐标点 。内部等边三角形(缩小一圈)为
。内部等边三角形(缩小一圈)为 ,含有
,含有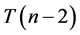 个点。
个点。
若记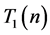 为满足
为满足 的整数边三角形个数,
的整数边三角形个数,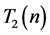 为满足
为满足 的非退化整数边三角形个数,(非退化的整数边三角形指的是三角形的内角中不能有两个直角或一个平角),那么对
的非退化整数边三角形个数,(非退化的整数边三角形指的是三角形的内角中不能有两个直角或一个平角),那么对 为偶数和奇数时的情况分别讨论如下:
为偶数和奇数时的情况分别讨论如下:
情形一:当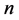 为奇数时,不妨设
为奇数时,不妨设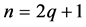 。
。
由 可知,
可知,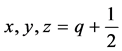 为满足条件的网格点的边界线(可参考图4左图
为满足条件的网格点的边界线(可参考图4左图 时),满足三角形条件的中间三角形为
时),满足三角形条件的中间三角形为 ,由三条边界线
,由三条边界线 包围在内,含有
包围在内,含有 个点。所以此时可以得出:
个点。所以此时可以得出: 。
。
情形二:当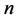 为偶数时,不妨设
为偶数时,不妨设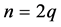 。
。
此时,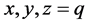 为满足条件的网格点的边界线(可参考图4右图
为满足条件的网格点的边界线(可参考图4右图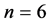 时),在每条边界线上有
时),在每条边界线上有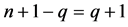 个点,满足三角形条件的中间三角形为
个点,满足三角形条件的中间三角形为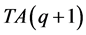 ,由三条边界线
,由三条边界线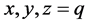 构成,含有
构成,含有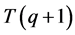 个点。所以此时可以得出:
个点。所以此时可以得出: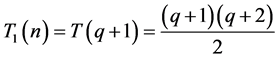 ,
,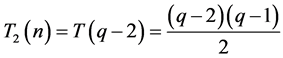 。
。
由以上讨论过程,我们可以得出如下推论。
推论3.1:(1)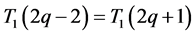 ;(2)
;(2)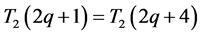 。
。
证明:(1)当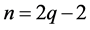 时,由上面公式,代入可计算出
时,由上面公式,代入可计算出 ;当
;当 时,由上面公式,代入可计算出
时,由上面公式,代入可计算出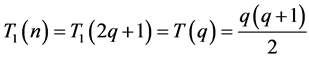 ,所以
,所以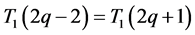 。
。
(2) 当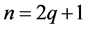 时,代入上面相关公式,则
时,代入上面相关公式,则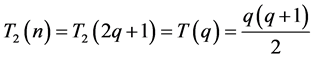 ;当
;当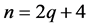 时,代入上面相关公式,则
时,代入上面相关公式,则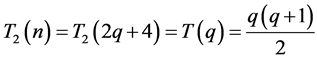 ,所以
,所以 。
。
在上述讨论网格点个数对应的三角形个数时,我们并没有把例如:三边长分别为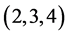 和
和 ,这样的两个全等的三角形作为同一个三角形考虑,所以在计数时出现了重复计数。为此,我们在考虑三角形的不全等性时,对应的网格点该怎么去重呢?
,这样的两个全等的三角形作为同一个三角形考虑,所以在计数时出现了重复计数。为此,我们在考虑三角形的不全等性时,对应的网格点该怎么去重呢?
定义3.1:若每个三角形的三边边长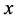 ,
,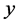 ,
, 所对应的坐标形式
所对应的坐标形式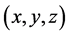 ,满足在置换下不会等价,则得到的三角形集合为不全等三角形。
,满足在置换下不会等价,则得到的三角形集合为不全等三角形。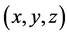 在置换下有六种等价形式:
在置换下有六种等价形式: ;
;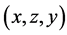 ;
;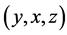 ;
;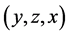 ;
;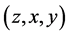 ;
;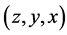 。
。
下面为计算方便先引入几个记号。
记 为
为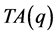 中不等价点个数;
中不等价点个数;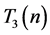 为周长为
为周长为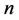 的不等价(不全等)整数边三角形的个数;
的不等价(不全等)整数边三角形的个数;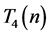 为周长为
为周长为 的不等价(不全等)非退化整数边三角形的个数。
的不等价(不全等)非退化整数边三角形的个数。
例:当 时,图5为
时,图5为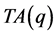 所对应的网格点图,不等价点包含在所画三角形边界及内部,则不等价点个数
所对应的网格点图,不等价点包含在所画三角形边界及内部,则不等价点个数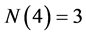 ;图6为
;图6为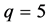 的情况,不等价点个数
的情况,不等价点个数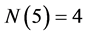 。
。
由以上定义,我们可以得到如下推论。
推论3.2:(1)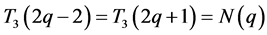 ;(2)
;(2) 。
。
证明:(1)当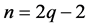 时,
时,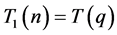 ,所以
,所以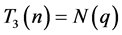 ;当
;当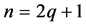 时,
时, ,所以
,所以 。所以
。所以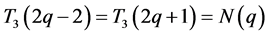 。
。
(2) 当 时,
时,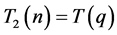 ,所以
,所以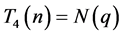 ;当
;当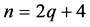 时,
时,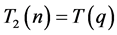 ,所以
,所以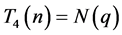 ;所以
;所以 。
。
我们可从以上性质中得出周长为 的不全等整数边三角形个数与对应网格状三角形内部满足条件的不等价点的个数关系。
的不全等整数边三角形个数与对应网格状三角形内部满足条件的不等价点的个数关系。
接着,我们将可以充分利用如上定义所得的一些关系式,推导出 的表达式,即为所求三角形的个数表达式。为此,我们可先证得如下关系式。
的表达式,即为所求三角形的个数表达式。为此,我们可先证得如下关系式。
定理3.1: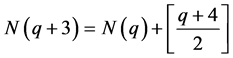 。
。
证明: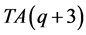 由
由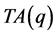 增大一圈获得,增加的外圈的三条边平均每条边有
增大一圈获得,增加的外圈的三条边平均每条边有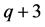 个点。那么不等价点增加个数讨论如下:
个点。那么不等价点增加个数讨论如下:
若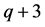 为偶数,则
为偶数,则 ;若
;若 为奇数,则
为奇数,则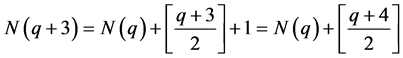 。
。
 q
= 4, N(q) = 3
q
= 4, N(q) = 3
Figure 5. Lattice point graph with q = 4
图5. q = 4的格点图
 q
= 5, N(q) = 4
q
= 5, N(q) = 4
Figure 6. Lattice point graph with q = 6
图6. q = 5的格点图
从以上定理我们得到了 内部的关系等式,进一步我们可以得到以下推论。
内部的关系等式,进一步我们可以得到以下推论。
推论3.3: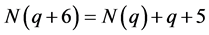 。
。
证明: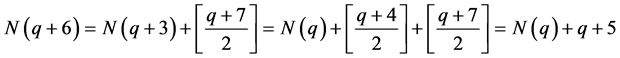 。
。
推论3.4:当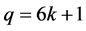 时,
时,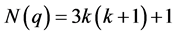 ;当
;当 时,
时,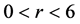 ,
, 。
。
证明:主要通过推论3.3中等式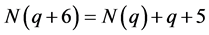 ,运用数列递推方法,可计算得该结论。具体推算步骤,见附录1。
,运用数列递推方法,可计算得该结论。具体推算步骤,见附录1。
结合以上推论以及推论3.2中(2)式,我们将可以推导出如下表达式。
推论3.5: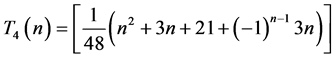 。
。
上述表达式的具体计算过程,详见附录2。至此,我们已通过网格点图中点的相关性质,相对应地求得了周长为 的不全等整数边三角形个数表达式。相比组合方法,这里通过图形中网格点的讨论来计数,更清晰易懂。
的不全等整数边三角形个数表达式。相比组合方法,这里通过图形中网格点的讨论来计数,更清晰易懂。
作为对以上证明题的延伸,这里我们讨论一下周长为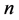 的不全等三角形的类型问题,讨论如下几个问题:
的不全等三角形的类型问题,讨论如下几个问题:
(1) 整数边长且周长为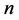 的不全等三角形中,含等腰三角形、等边三角形的个数为多少?
的不全等三角形中,含等腰三角形、等边三角形的个数为多少?
(2) 能否得出直角三角形、锐角三角形、钝角三角形的相关性质以及个数表达式?
2.3. 等腰、等边三角形个数表达式
在这部分,我们将研究上面所讨论的不全等三角形中含有的等腰三角形与等边
三角形的个数。为此,先介绍一下等腰三角形与等边三角形的定义。
定义4.1:三角形中,若有两条边长度相等,则这样的三角形称为等腰三角形;满足三条边长度都相等的三角形称为等边三角形。
研究三角形具体的边长关系,我们不难想到,可以和上述网格点图相结合,借助网格点图中点的性质,来计数特殊类型的三角形的个数。为此,我们先引入如下一些记号。
记 为整数边长且周长为
为整数边长且周长为 的不全等三角形中,含有的等腰三角形的个数;记
的不全等三角形中,含有的等腰三角形的个数;记 为上面讨论的三角形
为上面讨论的三角形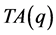 中,满足
中,满足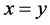 或
或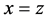 或
或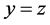 的不等价点
的不等价点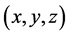 的个数。
的个数。
由上述符号定义,以及推论3.2中等式(2),我们可显然得到如下关系式。
推论 4.1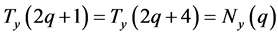 。
。
以上推论给出了周长为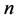 的整数边不全等等腰三角形个数
的整数边不全等等腰三角形个数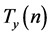 与满足三角形条件的内部三角形
与满足三角形条件的内部三角形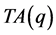 中不等价网格点的关系。所以,我们可以通过讨论
中不等价网格点的关系。所以,我们可以通过讨论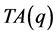 中不等价网格点的情况来得出
中不等价网格点的情况来得出 的值。因为
的值。因为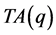 与
与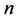 的奇偶性有关,所以我们先就
的奇偶性有关,所以我们先就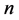 为奇数的情况讨论如下。
为奇数的情况讨论如下。
当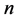 为奇数时,不妨设
为奇数时,不妨设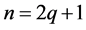 。
。
因为 ,所以满足条件的非退化整数边不全等三角形对应的网格点中内部三角形为
,所以满足条件的非退化整数边不全等三角形对应的网格点中内部三角形为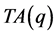 。下面需对
。下面需对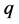 为奇数和
为奇数和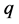 为偶数分情况讨论
为偶数分情况讨论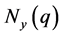 的个数。
的个数。
情形一:若 为偶数,即
为偶数,即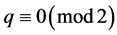 。
。
在三角形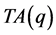 中,不等价点集中在
中,不等价点集中在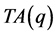 中一个六等划分直角三角形边界及其内部中。
中一个六等划分直角三角形边界及其内部中。
例:若 ,则
,则 ,
, 为如图7所示的网格正三角形,不等价点则包含在虚线构成的直角三角形边界以及内部,该虚线构成的三角形为
为如图7所示的网格正三角形,不等价点则包含在虚线构成的直角三角形边界以及内部,该虚线构成的三角形为 的六等划分。
的六等划分。
如上例所示,虚线构成的直角三角形边界其中两条即为: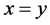 、
、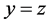 直线,这两条虚线上的点的个数即为我们所要求的满足
直线,这两条虚线上的点的个数即为我们所要求的满足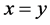 或
或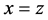 或
或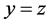 的不等价点个数,即
的不等价点个数,即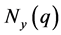 。下面分别讨论
。下面分别讨论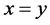 直线上点个数和
直线上点个数和 直线上点个数。(为计算方便,我们不妨设相邻网格点距离为1。)
直线上点个数。(为计算方便,我们不妨设相邻网格点距离为1。)

Figure 7. 6-partition of triangle
图7. 三角形的六等划分
(1) 在直线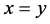 上,直角三角形的虚线长度为
上,直角三角形的虚线长度为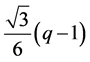 ,所含网格点的个数为
,所含网格点的个数为

(2) 在直线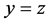 上,直角三角形的虚线长度为
上,直角三角形的虚线长度为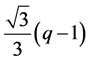 ,所含网格点的个数为
,所含网格点的个数为
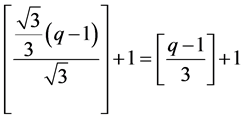
注意:当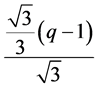 为整数,即
为整数,即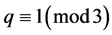 时,直线
时,直线 与直线
与直线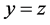 的交点恰为一个网格点,所以在计算网格点总个数时需减去1。
的交点恰为一个网格点,所以在计算网格点总个数时需减去1。
由以上(1)和(2)的讨论结果,我们可以得到以下推论。
推论4.2:当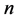 为奇数时,设
为奇数时,设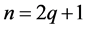 ,若
,若 为偶数,则
为偶数,则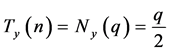 。
。
证明:由上面的讨论过程,我们可以得出,当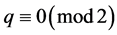 且
且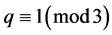 时,即
时,即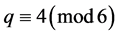 ,
,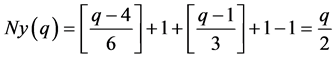 ;当
;当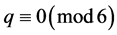 时,不妨设
时,不妨设 ,那么有
,那么有
 所以
所以 ;当
;当 时,同理可证得
时,同理可证得 。所以有
。所以有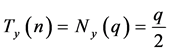 。
。
情形二:若 为奇数,即
为奇数,即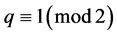 。
。
在三角形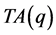 中,同样地,不等价点集中在
中,同样地,不等价点集中在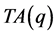 中一个六等划分直角三角形边界及其内部中。
中一个六等划分直角三角形边界及其内部中。
例:当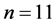 时,
时,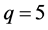 ,
,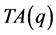 为如图8所示的网格正三角形,不等价点则包含在虚线构成的直角三角形边界以及内部。
为如图8所示的网格正三角形,不等价点则包含在虚线构成的直角三角形边界以及内部。
如上例所示,虚线构成的直角三角形边界其中两条即为: 、
、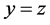 直线,这两条虚线上的点的个数即为我们所要求的满足
直线,这两条虚线上的点的个数即为我们所要求的满足 或
或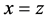 或
或 的不等价点个数,即
的不等价点个数,即 。下面分别讨论
。下面分别讨论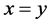 直线上点个数和
直线上点个数和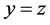 直线上点个数。(这里同样设相邻网格点距离为1。)
直线上点个数。(这里同样设相邻网格点距离为1。)

Figure 8. Lattice point equilateral triangle
图8. 网格正三角形
(1) 在直线 上,直角三角形的虚线长度为
上,直角三角形的虚线长度为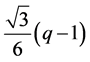 ,所含网格点的个数为
,所含网格点的个数为
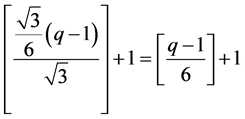 ;
;
(2) 在直线 上,直角三角形的虚线长度为
上,直角三角形的虚线长度为 ,所含网格点的个数为
,所含网格点的个数为
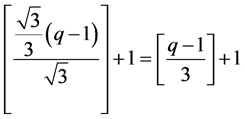 ;
;
注意:当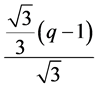 为整数,即
为整数,即 时,直线
时,直线 与直线
与直线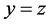 的交点恰为一个网格点,即为重点,所以在计算网格点总个数时需减去1。
的交点恰为一个网格点,即为重点,所以在计算网格点总个数时需减去1。
由以上(1)和(2)的讨论结果,我们可以得到如下推论。
推论4.3:当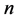 为奇数时,设
为奇数时,设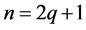 ,若
,若 为奇数,则
为奇数,则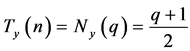 。
。
证明:由上面的讨论过程,我们可以得出,当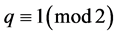 且
且 时,即
时,即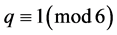 ,
,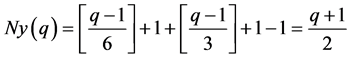 ;当
;当 时,不妨设
时,不妨设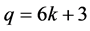 ,那么有
,那么有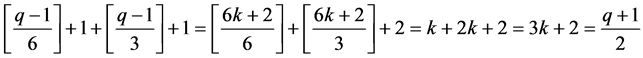 ,所以
,所以 ;当
;当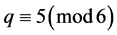 时,同理可证得
时,同理可证得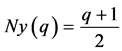 。所以有
。所以有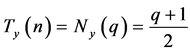 。
。
类似于如下对 为奇数情况的讨论过程,我们也可对
为奇数情况的讨论过程,我们也可对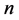 为偶数的情况进行分析,为免冗余,不再赘述。我们可得到如下结果。
为偶数的情况进行分析,为免冗余,不再赘述。我们可得到如下结果。
推论4.4:当 为偶数时,设
为偶数时,设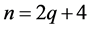 ,若
,若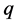 为偶数,则
为偶数,则 ;若
;若 为奇数,则
为奇数,则
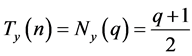
结合推论4.3和推论4.4,我们可显然得到以下表达式。
定理4.1:在周长为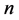 的不全等整数边三角形中,等腰三角形的个数
的不全等整数边三角形中,等腰三角形的个数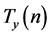 表达式如下:
表达式如下:
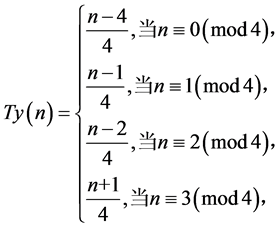
由此,我们已得出周长为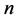 的不全等整数边三角形中,等腰三角形的个数表达式;对于等边三角形个数,则比较容易,因为等边三角形三边相等,所以只有当
的不全等整数边三角形中,等腰三角形的个数表达式;对于等边三角形个数,则比较容易,因为等边三角形三边相等,所以只有当 时,才含有一个等边三角形,其他情况的
时,才含有一个等边三角形,其他情况的 则不含有等边三角形。
则不含有等边三角形。
2.4. 直角、锐角、钝角三角形关系
在第三部分的空间网格点法证明三角形个数时,我们发现这样一个有趣的现象:当周长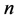 为偶数时,网格点图中满足三角形条件的内部网格三角形与周长为
为偶数时,网格点图中满足三角形条件的内部网格三角形与周长为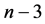 时对应的内部三角形是边长相等的正三角形。由推论3.1中(2)式
时对应的内部三角形是边长相等的正三角形。由推论3.1中(2)式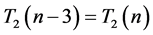 (
(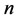 为偶数)也可看出该现象。于是,我们产生疑问,那两个相同正三角形中对应位置格点所表示的三角形类型是否也相同呢?这里主要考虑三角形的直角、锐角、钝角性。为此,我们先介绍一下各三角形类型的定义。
为偶数)也可看出该现象。于是,我们产生疑问,那两个相同正三角形中对应位置格点所表示的三角形类型是否也相同呢?这里主要考虑三角形的直角、锐角、钝角性。为此,我们先介绍一下各三角形类型的定义。
定义5.1:若一个三角形中,两边边长的平方和等于第三边边长的平方,那么这样的三角形称为直角三角形。例如,一个三边边长分别为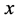 、
、 、
、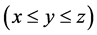
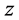 的三角形,若满足
的三角形,若满足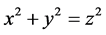 ,则这个三角形为直角三角形。
,则这个三角形为直角三角形。
定义5.2:若一三边长分别为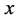 、
、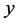 、
、
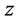 的三角形,满足
的三角形,满足 ,则称该三角形为锐角三角形。
,则称该三角形为锐角三角形。
定义5.3:若一三边长分别为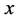 、
、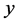 、
、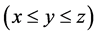
 的三角形,满足
的三角形,满足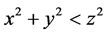 ,则称该三角形为钝角三角形。
,则称该三角形为钝角三角形。
定义5.4:若一正整数组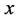 、
、 、
、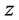 满足等式
满足等式 ,则称
,则称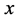 ,
,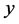 ,
,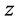 为勾股数。
为勾股数。
在给出以上各类型三角形定义后,为方便研究三角形边长的关系,我们需借助直角三角形的边长的一个特殊性质,叙述如下。
定理5.1:商高定理:任意一组素勾股数 ,
, ,
, 都可以表示为如下形式:
都可以表示为如下形式: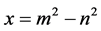 ,
, ,
, ,其中
,其中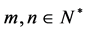 ,
,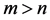 。
。
由以上定理,我们可以得出:对于不互素的勾股数 ,
,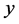 ,
, ,则可表示为
,则可表示为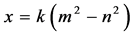 ,
,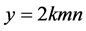 ,
,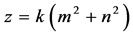 ,其中
,其中 ,
, 。
。
下面,我们将先讨论周长为 的三角形中含直角三角形的情况。
的三角形中含直角三角形的情况。
推论5.1:若在周长为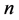 的不全等整数边三角形中,含有直角三角形,则
的不全等整数边三角形中,含有直角三角形,则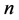 一定为偶数。
一定为偶数。
证明:由定理4.1,若该直角三角形三边互素,则可表示成定理中所述形式,则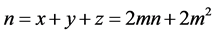 ,所以
,所以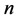 为偶数;若三边不互素,则三边
为偶数;若三边不互素,则三边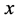 ,
, ,
,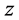 可表示为
可表示为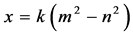 ,
, ,
,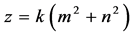 ,其中
,其中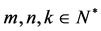 ,
,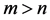 ,所以
,所以 ,所以
,所以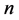 仍为偶数。
仍为偶数。
正如本部分的开头所述,既然上面推论中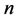 为偶数,那么周长为
为偶数,那么周长为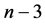 的三角形网格点图中对应于
的三角形网格点图中对应于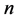 中直角三角形格点位置的点所表示的三角形是否仍为直角三角形呢?
中直角三角形格点位置的点所表示的三角形是否仍为直角三角形呢?
定理5.2:在周长为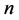 的含直角三角形的不全等整数边三角形中,设直角三角形三边分别为
的含直角三角形的不全等整数边三角形中,设直角三角形三边分别为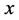 ,
, ,
,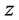 ,满足
,满足 ,则在周长为
,则在周长为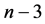 的整数边三角形中,三边长分别为
的整数边三角形中,三边长分别为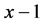 ,
,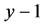 ,
, 的三角形一定为钝角三角形。
的三角形一定为钝角三角形。
证明:首先,证明该三边一定能构成三角形。因为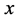 ,
, ,
, 满足
满足 ,所以
,所以 ,
,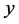 ,
,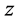 可表示为
可表示为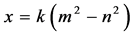 ,
,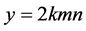 ,
,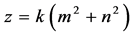 ,其中
,其中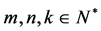 ,
,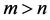 。要证三边
。要证三边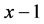 ,
,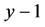 ,
,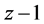 能构成三角形,即证
能构成三角形,即证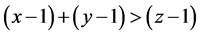 ,即证
,即证 ,即证
,即证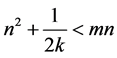 ,因为
,因为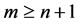 ,所以上式成立,故得证该三边
,所以上式成立,故得证该三边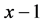 ,
,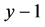 ,
,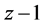 能构成三角形。接着,证明该三角形能构成钝角三角形。即需证
能构成三角形。接着,证明该三角形能构成钝角三角形。即需证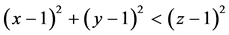 ,代入
,代入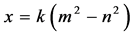 ,
,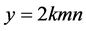 ,
, ,化简得
,化简得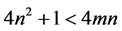 ,因为
,因为 ,所以上式成立,故得证三边长分别为
,所以上式成立,故得证三边长分别为 ,
,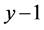 ,
,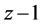 的三角形为钝角三角形。
的三角形为钝角三角形。
由以上定理,结合推论3.2,我们可以知道,因为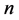 为偶数时,周长为
为偶数时,周长为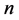 的三角形网格点中内部满足条件的网格三角形与周长为
的三角形网格点中内部满足条件的网格三角形与周长为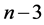 的三角形网格点中的内部满足条件的网格三角形是一样的,所以我们研究它们对应位置点的三角形类型关系。由定理5.2,我们得出,对应于周长为
的三角形网格点中的内部满足条件的网格三角形是一样的,所以我们研究它们对应位置点的三角形类型关系。由定理5.2,我们得出,对应于周长为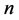 (
(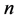 为偶数)的直角三角形点在周长为
为偶数)的直角三角形点在周长为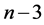 中一样位置的点对应的三角形一定为钝角三角形。
中一样位置的点对应的三角形一定为钝角三角形。
例:图9为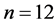 和
和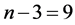 的例子,它们的两个对应点
的例子,它们的两个对应点 和
和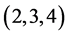 分别表示的三角形是:边长为3,4,5的直角三角形与边长为2,3,4的钝角三角形。
分别表示的三角形是:边长为3,4,5的直角三角形与边长为2,3,4的钝角三角形。
下面,我们继续探究,对应位置点锐角、钝角三角形的类型是如何变化的?这里,我们先解释一下,把对应位置点这种关系还原到三角形问题,实则对应于这样一个问题:对于一个周长为偶数的整数边三角形,在每条边减少1后,是否仍保持三角形类型?如果不保持,有何变化规律?
从上面的定理5.2,我们可以知道,周长为偶数的直角三角形在每条边减少1后,将变成一个钝角三角形。那若原来为锐角三角形或钝角三角形时,情况是如何的呢?于是,我们得到以下定理。
定理5.3:周长为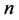 (
(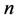 为偶数)的整数边钝角三角形,设三角形三边分别为
为偶数)的整数边钝角三角形,设三角形三边分别为 ,
,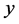 ,
,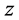 ,满足
,满足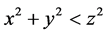 ,则在周长为
,则在周长为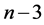 的整数边三角形中,三边长分别为
的整数边三角形中,三边长分别为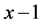 ,
,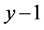 ,
, 的三角形一定仍为钝角三角形。
的三角形一定仍为钝角三角形。
证明:首先证明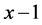 ,
,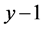 ,
,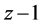 仍能构成三角形,即需证
仍能构成三角形,即需证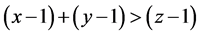 ,
,
即需证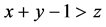 ,由
,由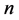 为偶数显然可得。下面证
为偶数显然可得。下面证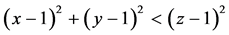 ,即需证
,即需证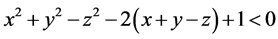 ,显然成立,故得证。
,显然成立,故得证。
注:当上述定理中改为“锐角三角形”时,并不保持结果仍为锐角三角形。反例如下,取三角形三边长为9、39、40,构成一个锐角三角形,但对应每边减少1后,8、38、39这三边构成的三角形为钝角三角形。
 n
= 12, n − 3 = 9
n
= 12, n − 3 = 9
Figure 9. Lattice point equilateral triangle
图9. 网格正三角形
综上,周长为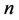 (
(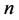 为偶数)与周长为
为偶数)与周长为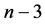 的三角形对应的网格点图中,对应位置点所表示的钝角三角形类型是相同的,直角三角形对应于钝角三角形,锐角三角形是变化的。也即周长为
的三角形对应的网格点图中,对应位置点所表示的钝角三角形类型是相同的,直角三角形对应于钝角三角形,锐角三角形是变化的。也即周长为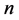 (
(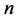 为偶数)的整数边三角形,各边减少1后,钝角三角形保持三角形类型不变,直角三角形变为钝角三角形,锐角三角形变化不定。
为偶数)的整数边三角形,各边减少1后,钝角三角形保持三角形类型不变,直角三角形变为钝角三角形,锐角三角形变化不定。
以上结论能否用于求周长为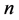 的整数边三角形中所含各类型三角形的个数,还有待进一步研究。
的整数边三角形中所含各类型三角形的个数,还有待进一步研究。
基金项目
国家自然科学基金(数学基地科研训练及能力提高)项目资助,上海市科学技术委员会的资助,资助课题编号为13dz2260400。
文章引用
蔡雅静,镡镇鹂,晁福刚,任韩. 整数边三角形个数的组合与几何证明方法
Combinatorial and Geometric Proofs of the Number of Triangles with Integer Sides[J].
应用数学进展, 2015, 04(03): 246-261. http://dx.doi.org/10.12677/AAM.2015.43031
参考文献 (References)
- 1. Comtet, L. (1974) Advanced combinatorics: The art of finite and infinite expansions. Springer. http://dx.doi.org/10.1007/978-94-010-2196-8
- 2. Andrews, G.E. (1979) A note on partitions and triangles with integer sides. The American Mathematical Monthly, 86, 477-478. http://dx.doi.org/10.2307/2320420
- 3. Euler, L. (1751) Observationes analyticae variae de combinationibus. Commentarii Academiae Scientiarum Imperialis Pe-tropolitanae, 13, 1741-1743.
- 4. Gordon, B. (1961) A combinatorial generalization of the Rogers-Ramanujan identities. American Journal of Mathematics, 83, 393-399. http://dx.doi.org/10.2307/2372962
- 5. Hardy, G.H. and Ramanujan, S. (1918) Asymptotic formulaæ in combinatory analysis. Proceedings of the London Mathematical Society, 2, 75-115. http://dx.doi.org/10.1112/plms/s2-17.1.75
- 6. Hardy, G.H. and Wright, E.M. (1979) An introduction to the theory of numbers. Oxford University Press, Oxford.
- 7. MacMahon, P.A. (1984) Combinatory analysis. Courier Dover Publications, Mineola.
- 8. Rademacher, H. (1938) On the partition function p (n). Proceedings of the London Mathematical Society, 2, 241-254. http://dx.doi.org/10.1112/plms/s2-43.4.241
- 9. Sylvester, J.J. and Franklin, F. (1882) A constructive theory of partitions, arranged in three acts, an interact and an exodion. American Journal of Mathematics, 5, 251-330. http://dx.doi.org/10.2307/2369545
- 10. Bindner, D.J. and Erickson, M. (2012) Alcuin’s sequence. The American Mathematical Monthly, 119, 115-121. http://dx.doi.org/10.4169/amer.math.monthly.119.02.115
- 11. Singmaster, D. (1990) Triangles with integer sides and sharing barrels. College Mathematics Journal, 21, 278-285. http://dx.doi.org/10.2307/2686363
- 12. Jordan, J.H., Walch, R. and Wisner, R.J. (1979) Triangles with integer sides. American Mathematical Monthly, 86, 686-689. http://dx.doi.org/10.2307/2321300
- 13. Wilf, H.S. (2009) Lectures on integer partitions. (Unpublished)
附录1
递推公式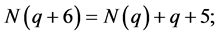
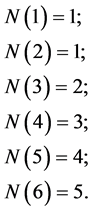
(1) 当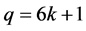 时
时
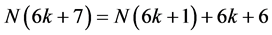
令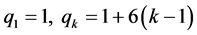
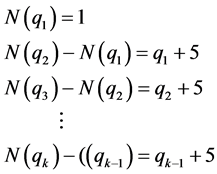
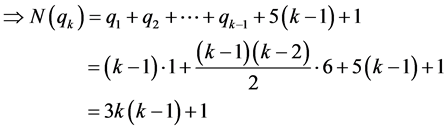

(2) 当 时,
时,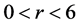
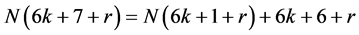
令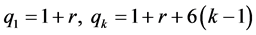

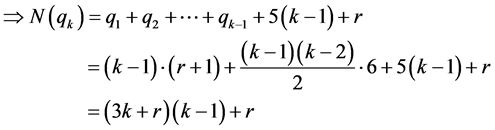
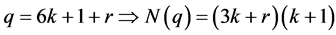
附录2
 表达式的推导过程
表达式的推导过程
我们要证结果: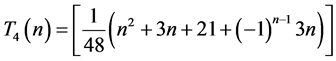 。
。
(1) 当 为奇数时,不妨设
为奇数时,不妨设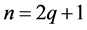
由推论3.4,我们把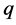 分情况讨论,分别讨论当
分情况讨论,分别讨论当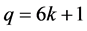 和当
和当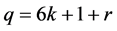 ,
,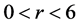 时。
时。
当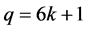 ,
,
 ,
,
 ,
,
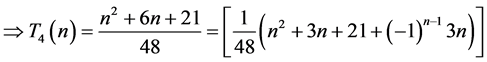 。
。
当 ,
,
同上可证得 。
。
(2) 当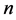 为偶数时,不妨设
为偶数时,不妨设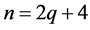
同样把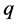 分情况讨论。
分情况讨论。
当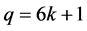 ,
,
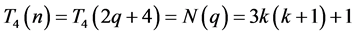
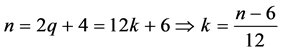

当 ,
,
同上可证得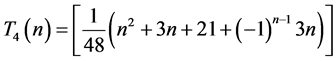 。
。