Advances in Applied Mathematics
Vol.05 No.04(2016), Article ID:18972,9
pages
10.12677/AAM.2016.54070
Analysis on Stability and Hopf Bifurcation in a Delayed Epidemic Model with Double Epidemic Hypothesis
Jiarong Lu, Jiangang Zhang, Hongwei Luo, Jun Yin, Qin Pang
Department of Mathematics, Lanzhou Jiaotong University, Lanzhou Gansu

Received: Oct. 26th, 2016; accepted: Nov. 10th, 2016; published: Nov. 18th, 2016
Copyright © 2016 by authors and Hans Publishers Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/



ABSTRACT
This paper mainly investigates the stability and Hopf bifurcation in a delayed epidemic model system with double epidemic hypothesis. We study the stability of the unique positive equilibrium for the system under different conditions. By analyzing the distribution of characteristic roots of corresponding linearized system, we obtain the conditions for keeping the system to be stable. Moreover, it is illustrated that the Hopf bifurcation will occur when the delay passes through a critical value. Then we use the MATLAB numerical simulations for justifying the theoretical results.
Keywords:Epidemic Model with Double Epidemic Hypothesis, Time Delay, Stability, Hopf Bifurcation

带有时滞的双传染病假设模型稳定性 及Hopf分岔分析
卢加荣,张建刚,罗宏伟,殷俊,庞琴
兰州交通大学数理学院,甘肃 兰州

收稿日期:2016年10月26日;录用日期:2016年11月10日;发布日期:2016年11月18日

摘 要
本文主要分析带有时滞影响下的双传染病假设模型的稳定性及Hopf分岔,研究了不同情况下的系统唯一的正平衡点的稳定性,并通过分析相应线性系统的特征根的分布,得到了使得系统平衡的条件。然而,当时滞的值通过一个临界值的时候,Hopf分岔就会发生。最后, 运用MATLAB数值模拟去验证得到的理论结果。
关键词 :双传染病假设模型,时滞,稳定性,Hopf分岔

1. 引言
在近几年,对于传染病的研究吸引了大量学者的研究,并且运用数学模型建立了很多传染病模型 [1] - [6] ,比如一些经典的模型,HIV模型。在文献 [7] 中将饱和治愈函数引入带有饱和发病率的传染病模型,他们对于无病平衡点和地方病平衡点的存在性和全局渐近稳定性提供了充分条件。另外,在文献 [8] 中,研究了结合免疫应答的HIV模型的稳定性及其分岔现象,借助于数学分析,他们从一个出现向后的分岔曲线感染平衡并且可以连续到基本再生数小于整体的地方找到了一种新的分支。在这项研究之前,文献 [9] 在HIV模型中引入了两个时滞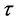 ,他们假设病毒的产生发生在病毒完全进入感染体之后,因此,病毒生产细胞的补充时间
,他们假设病毒的产生发生在病毒完全进入感染体之后,因此,病毒生产细胞的补充时间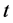 是由新感染细胞的时间
是由新感染细胞的时间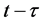 组成,并在时间
组成,并在时间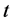 上仍然存活。接着,他们运用Beretta和Kuang介绍的分析方法获得了Hopf分岔存在的充分条件。同样的,在文献 [10] 中作者研究了带有恒定时滞的SIS传染病模型,在这篇文章中,还采用了微分不等式和一些新颖的方法研究地方病平衡点稳定性。但是在文献 [11] 中,建立了随机的SIS传染病系统,给出了在灭绝和持续生存之间平衡的充分条件,并找到了一个阈值,使得白噪声强度充分小,随机因素不影响系统的稳定性。
上仍然存活。接着,他们运用Beretta和Kuang介绍的分析方法获得了Hopf分岔存在的充分条件。同样的,在文献 [10] 中作者研究了带有恒定时滞的SIS传染病模型,在这篇文章中,还采用了微分不等式和一些新颖的方法研究地方病平衡点稳定性。但是在文献 [11] 中,建立了随机的SIS传染病系统,给出了在灭绝和持续生存之间平衡的充分条件,并找到了一个阈值,使得白噪声强度充分小,随机因素不影响系统的稳定性。
一些普遍的传染病模型都建立了一种疾病与总体之间的关系,而在文献 [12] 中给出了一种双传染病假设的SIS模型,即存在两种病毒A和B,每一种病毒都是平行感染,并且已受病毒A感染的细胞可以免受病毒B的感染。
通常来讲,时滞在生物系统中是相当常见的现象 [13] [14] [15] [16] ,对于病毒感染过程也是一样。事实上,在本文中,受感染者具有自我恢复能力和人工治愈的恢复期,不同疾病感染者有不同的能力和时间。所以,在本文中,我们引入了两个不同的时滞,然后通过系统的特征方程及其特征值的性质,来研究系统平衡点处的稳定性和Hopf分岔及其周期解的存在性,最终得到时滞的一个临界值,从而得到发生Hopf分岔的条件。
在这篇文章中,在一个双传染病假设的SIS模型中引入了两个不同的时滞,
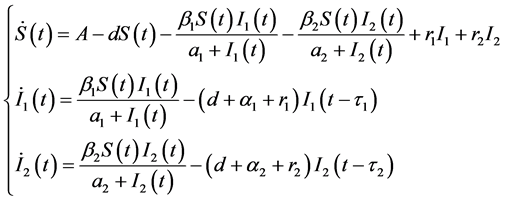 (1)
(1)
其中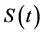 表示易感染病毒人群的数量,
表示易感染病毒人群的数量,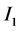 和
和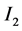 分别是在时间
分别是在时间 内被病毒A和病毒B感染的人群,易受感染的人群规模是一个常数
内被病毒A和病毒B感染的人群,易受感染的人群规模是一个常数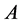 。
。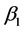 和
和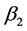 是接触率,
是接触率,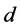 是自然死亡率,
是自然死亡率, 和
和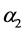 是疾病的死亡率,
是疾病的死亡率,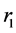 和
和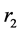 分别是两种疾病的治愈率,
分别是两种疾病的治愈率,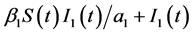 和
和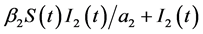 表示两种传染病的发病饱和率,
表示两种传染病的发病饱和率,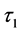 和
和 分别表示两种疾病的自我恢复能力和人工治愈的恢复期。
分别表示两种疾病的自我恢复能力和人工治愈的恢复期。
2. 平衡点及局部稳定性
下面将会提供一些基本的引理及双传染病模型稳定性和发生Hopf分岔的主要结论。
系统(1)存在平衡点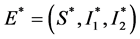
其中
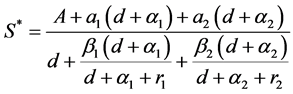
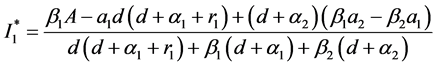
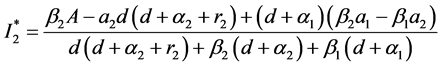
当且仅当
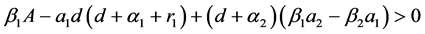 ,
,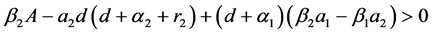
时,系统(1)有唯一的正平衡点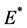 。
。
接着,运用如下线性化转换式
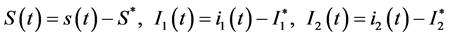
最终系统变成如下系统(2)
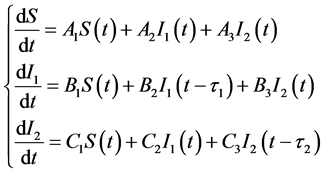 (2)
(2)
其中
 ,
,
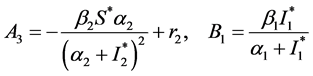


运用Maple可以得到如下超越特征方程
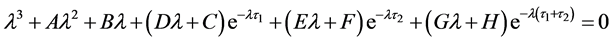 (3)
(3)
若 ,(3)式变为
,(3)式变为
 (4)
(4)
其中

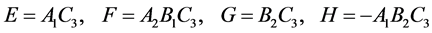
则当且仅当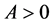 和
和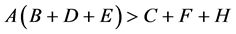 时,方程(4)的所有根有负实部,所以系统在平衡点
时,方程(4)的所有根有负实部,所以系统在平衡点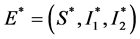 处局部渐进稳定。
处局部渐进稳定。
3. Hopf分岔的存在性
1) 当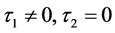 时。
时。
设 是方程(3)的一个根,代入可得
是方程(3)的一个根,代入可得
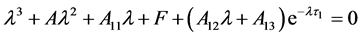 (5)
(5)
其中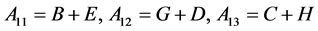
分离实部与虚部,可得
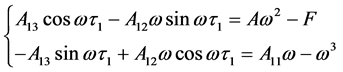 (6)
(6)
从上式可得
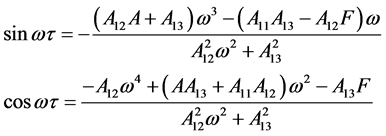 (7)
(7)
进而上式可化为
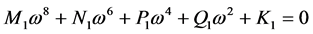 (8)
(8)
其中
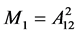 ,
,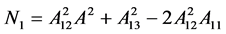 ,
,

 ,
,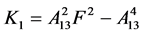
令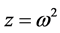 ,有
,有
 (9)
(9)
令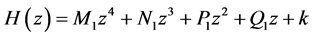 。
。
通过分析方程(9),当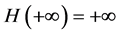 时,若有条件1:
时,若有条件1: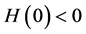 ,此时方程(9)至少有一个正根,假设(9)式有4个正根分别为
,此时方程(9)至少有一个正根,假设(9)式有4个正根分别为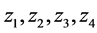 ,则方程(8)也有4个正根为
,则方程(8)也有4个正根为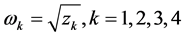 。
。
从方程(7),定义如下式子
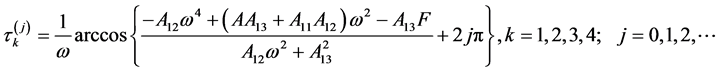
则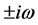 是方程(5)的一对纯虚根
是方程(5)的一对纯虚根
令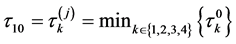 ,通过以上的分析,可以得到以下引理。
,通过以上的分析,可以得到以下引理。
首先,令
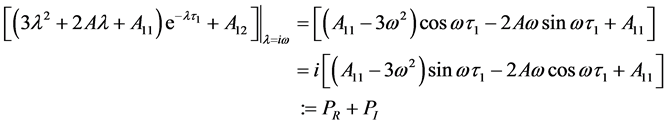
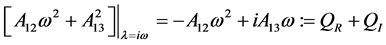
假设条件2: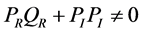 。
。
引理1:令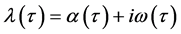 是方程(5)的根,且满足在
是方程(5)的根,且满足在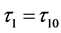 附近,有
附近,有 和
和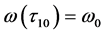 则如下式子成立
则如下式子成立
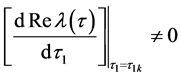
证明 将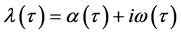 代入方程(5),且对
代入方程(5),且对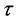 进行两边求积分,可以得到
进行两边求积分,可以得到
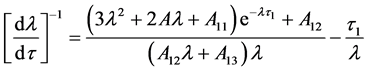
则

因此,若条件2成立,则
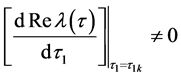
证毕。
综上所述,可以总结出如下定理。
定理1:对于系统(2),如下结论成立
假设条件2成立,当 从0开始变化时,存在一个临界值
从0开始变化时,存在一个临界值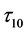 ,使得当
,使得当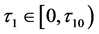 时,系统在正平衡点
时,系统在正平衡点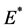 处局部渐进稳定,当
处局部渐进稳定,当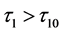 时不稳定。因此,当
时不稳定。因此,当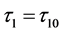 时,系统(1)在正平衡点
时,系统(1)在正平衡点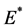 处发生Hopf分岔。
处发生Hopf分岔。
2) 当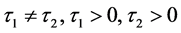 时。
时。
前面已经分析了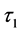 的稳定性,所以当存在双时滞影响的时候,需要在
的稳定性,所以当存在双时滞影响的时候,需要在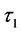 处于它的稳定区间的前提下,即
处于它的稳定区间的前提下,即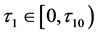 ,令
,令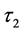 为一个参数。因此,此时的超越特征方程即为方程(3)。
为一个参数。因此,此时的超越特征方程即为方程(3)。
令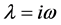 是方程(3)的一个根,代入且分离方程的实部与虚部可得
是方程(3)的一个根,代入且分离方程的实部与虚部可得
 (10)
(10)
消去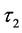 ,方程(10)变成如下形式
,方程(10)变成如下形式
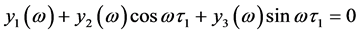 (11)
(11)
假设条件3:方程(11)有至少有限个正根为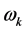 ,所以存在一个序列
,所以存在一个序列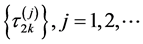 ,使得方程(10)成立。
,使得方程(10)成立。
由方程(10),定义
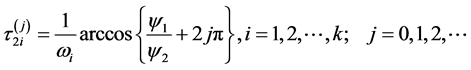
其中
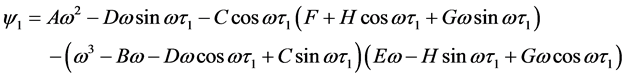
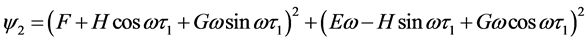
则当 时,
时,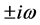 是方程(3)的一对纯虚根。
是方程(3)的一对纯虚根。
令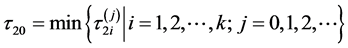 ,当
,当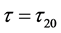 时,方程(3)有一对纯虚根
时,方程(3)有一对纯虚根 ,因此,当
,因此,当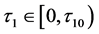 时,可以总结出以下引理。
时,可以总结出以下引理。
引理2:令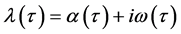 是方程(3)的根,且满足在
是方程(3)的根,且满足在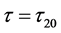 附近,有
附近,有 和
和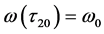 则如下式子成立
则如下式子成立
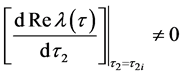
证明首先将方程(3)对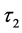 进行两边求积分,可以得到
进行两边求积分,可以得到
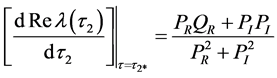
其中
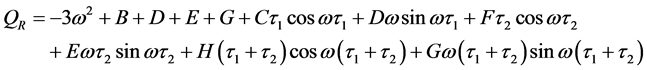
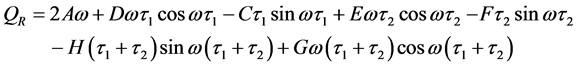
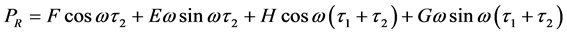
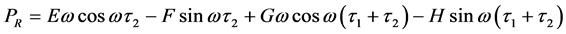
如果条件4: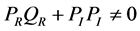 成立,则有
成立,则有
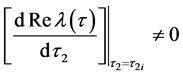
证毕。
所以根据偏微分方程的一般Hopf分岔定理 [17] [18] ,可以得到如下定理
定理2 对于系统(1),若条件3和条件4成立,且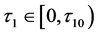 。
。
i) 当 时,系统(1)在正平衡点
时,系统(1)在正平衡点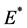 处是局部渐进稳定的,当
处是局部渐进稳定的,当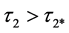 时趋于不稳定。
时趋于不稳定。
ii) 当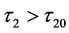 时,系统(1)在正平衡点
时,系统(1)在正平衡点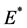 处发生Hopf分岔。
处发生Hopf分岔。
4. 数值模拟
在这一节中,我们给出具体的数值模拟结果来对前面分析的结果进行说明,对于系统(1),将参数赋予以下值,
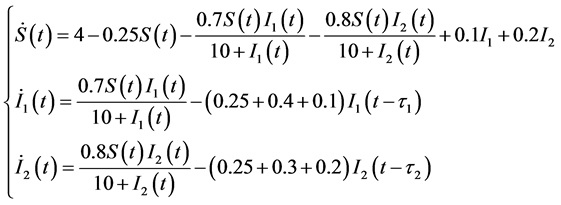 (12)
(12)
通过系统(12)可求得正平衡点为 。
。
首先,当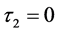 ,
,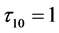 时,可以得到相应的时间响应图,如图1所示。
时,可以得到相应的时间响应图,如图1所示。
 (a)
(a)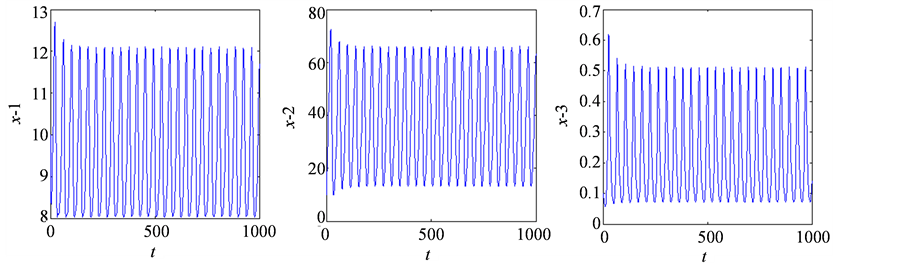 (b)
(b)
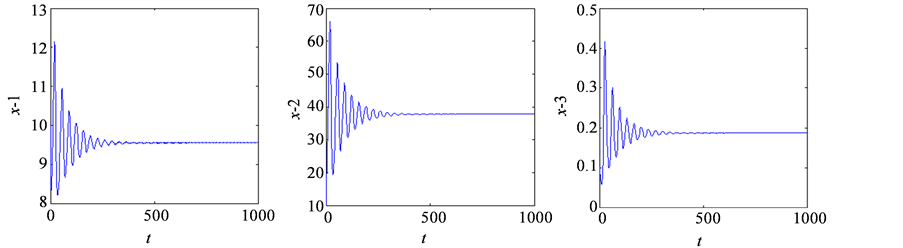
Figure 1. The positive equilibrium of system (1) is locally asymptotically stable when  (Figure 1(a)), the hopf bifurcation will occur in the equilibrium of system (1) when
(Figure 1(a)), the hopf bifurcation will occur in the equilibrium of system (1) when 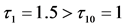 (Figure 1(b)), where initial value is “10, 10, 0. 1”
(Figure 1(b)), where initial value is “10, 10, 0. 1”
图1. 当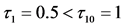 时,系统(1)在正平衡点处呈现局部渐进稳定的(如图1(a)),当
时,系统(1)在正平衡点处呈现局部渐进稳定的(如图1(a)),当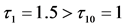 时,系统(1)在平衡点处发生Hopf分岔(如图1(b))所示,其中初值为“10, 10, 0. 1”
时,系统(1)在平衡点处发生Hopf分岔(如图1(b))所示,其中初值为“10, 10, 0. 1”

 (a)(b)
(a)(b)
Figure 2. The positive equilibrium of system (1) is locally asymptotically stable when 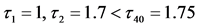 (Figure 2(a)) , the hopf bifurcation will occur in the equilibrium of system (1) when
(Figure 2(a)) , the hopf bifurcation will occur in the equilibrium of system (1) when 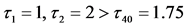 (Figure 2(b)) , where initial value is “11, 0. 1, 1”
(Figure 2(b)) , where initial value is “11, 0. 1, 1”
图2. 当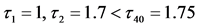 时,系统(1)在正平衡点处呈现局部渐进稳定的(如图2(a)),当
时,系统(1)在正平衡点处呈现局部渐进稳定的(如图2(a)),当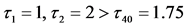 时,系统(1)在平衡点处发生Hopf分岔(如图2(b))所示,其中初值为“11, 0. 1, 1”
时,系统(1)在平衡点处发生Hopf分岔(如图2(b))所示,其中初值为“11, 0. 1, 1”
然后,我们在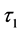 的稳定区间下讨论
的稳定区间下讨论 ,此时将
,此时将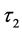 作为一个参数。令
作为一个参数。令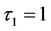 并且当
并且当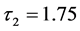 时,当
时,当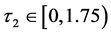 时,系统在平衡点
时,系统在平衡点 处是局部渐进稳定的,当
处是局部渐进稳定的,当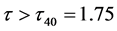 时,系统将会发生Hopf分岔,如图2所示。
时,系统将会发生Hopf分岔,如图2所示。
5. 总结
本文主要分析了引入不同时滞后的双传染病模型的稳定性与Hopf分岔,研究了在不同情况下系统平衡点处分岔的存在性及其局部稳定性,接着得到稳定的条件,及其发生Hopf分岔时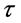 的临界值。最后,用MATLAB进行数值模拟,验证所得到的结论。在以后的工作中,我们会对分岔、混沌的控制进行进一步的研究。
的临界值。最后,用MATLAB进行数值模拟,验证所得到的结论。在以后的工作中,我们会对分岔、混沌的控制进行进一步的研究。
基金项目
国家自然科学基金(11161027, 61364001);甘肃省科技支撑(144GKCA018)。
文章引用
卢加荣,张建刚,罗宏伟,殷俊,庞琴. 带有时滞的双传染病假设模型稳定性及Hopf分岔分析
Analysis on Stability and Hopf Bifurcation in a Delayed Epidemic Model with Double Epidemic Hypothesis[J]. 应用数学进展, 2016, 05(04): 605-613. http://dx.doi.org/10.12677/AAM.2016.54070
参考文献 (References)
- 1. Kang, H.Y. and Fu, X.C. (2015) Epidemic Spreading and Global Stability of an SIS Model with an Infective Vector on Complex Networks. Communications in Nonlinear Science and Numerical Simulation, 27, 30-39. http://dx.doi.org/10.1016/j.cnsns.2015.02.018
- 2. Li, C.H. (2015) Dynamics of a Network-Based SIS Epidemic Model with Nonmonotone Incidence Rate. Physica A: Statistical Mechanics and its Applications, 427, 234-243. http://dx.doi.org/10.1016/j.physa.2015.02.023
- 3. Economoua, A., Gómez-Corral, A. and López-García, M. (2015) A Stochastic SIS Epidemic Model with Heterogeneous Contacts. Physica A: Statistical Mechanics and its Applications, 421, 78-97. http://dx.doi.org/10.1016/j.physa.2014.10.054
- 4. Zhang, J.C. and Sun, J.T. (2014) Stability Analysis of an SIS Epidemic Model with Feedback Mechanism on Networks. Physica A: Statistical Mechanics and its Applications, 394, 24-32. http://dx.doi.org/10.1016/j.physa.2013.09.058
- 5. Li, J., Zhao, Y.L. and Zhu, H.P. (2015) Bifurcation of an SIS Model with Nonlinear Contact Rate. Journal of Mathematical Analysis and Applications, 432, 1119-1138. http://dx.doi.org/10.1016/j.jmaa.2015.07.001
- 6. Cai, Y.L., Kang, Y., Banerjee, M. and Wang, W.M. (2015) A Stochastic SIRS Epidemic Model with Infectious Force under Intervention Strategies. Journal of Differential Equations, 259, 7463-7502. http://dx.doi.org/10.1016/j.jde.2015.08.024
- 7. Zhou, T.T., Zhang, W.P. and Lu, Q.Y. (2014) Bifurcation Analysis of an SIS Epidemic Model with Saturated Incidence Rate and Saturated Treatment Function. Applied Mathematics and Computation, 226, 288-305. http://dx.doi.org/10.1016/j.amc.2013.10.020
- 8. Luo, J.F., Wang, W.D., Chen, H.Y. and Fu, R. (2016) Bifurcations of a Ma-thematical Model for HIV Dynamics. Journal of Mathematical Analysis and Applications, 434, 837-857. http://dx.doi.org/10.1016/j.jmaa.2015.09.048
- 9. Hao, P.M., Fan, D.J., Wei, J.J. and Liu, Q.H. (2012) Dynamic Behaviors of a Delayed HIV Model with Stage-Structure. Communications in Nonlinear Science and Numerical Simulation, 17, 4753-4766. http://dx.doi.org/10.1016/j.cnsns.2012.04.004
- 10. Liu, B.W. (2015) Convergence of an SIS Epidemic Model with a Constant Delay. Applied Mathematics Letters, 49, 113-118. http://dx.doi.org/10.1016/j.aml.2015.04.012
- 11. Zhao, Y.N. and Jiang, D.Q. (2014) The Threshold of a Stochastic SIS Epidemic Model with Vaccination. Applied Mathematics and Computation, 243, 718-727. http://dx.doi.org/10.1016/j.amc.2014.05.124
- 12. Meng, X.Z., Zhao, S.N., Feng, T. and Zhao, T.H. (2016) Dynamics of a Novel Nonlinear Stochastic SIS Epidemic Model with Double Epidemic Hypothesis. Journal of Mathematical Analysis and Applications, 433, 227-242. http://dx.doi.org/10.1016/j.jmaa.2015.07.056
- 13. Huo, H.F. and Ma, Z.P. (2010) Dynamics of a Delayed Epidemic Model with Non-Monotonic Rate. Communications in Nonlinear Science and Numerical Simulation, 15, 459-468. http://dx.doi.org/10.1016/j.cnsns.2009.04.018
- 14. Çelik, C. (2008) The Stability and Hopf Bifurcation for a Predator-Prey System with Time Delay. Chaos, Solitons Fractals, 37, 87-99. http://dx.doi.org/10.1016/j.chaos.2007.10.045
- 15. Zhang, L.Y. (2015) Hopf Bifurcation Analysis in a Monod-Haldane Predator-Prey Model with Delays and Diffusion. Applied Mathematical Mod-elling, 39, 1369-1382. http://dx.doi.org/10.1016/j.apm.2014.09.007
- 16. Çelik, C. (2009) Hopf Bifurcation of a Ratio-Dependent Predator-Prey System with Time Delay. Chaos, Solitons Fractals, 42, 1474-1484. http://dx.doi.org/10.1016/j.chaos.2009.03.071
- 17. Hale, J.K. (1977) Theory of Functional Differential Equation. Springer-Verlag, New York. http://dx.doi.org/10.1007/978-1-4612-9892-2
- 18. Hassard, B.D., Kazarinoff, N.D. and Wan, Y.H. (1981) Theory and Applica-tions of Hopf Bifurcation. Cambridge University Press, Cambridge.