Advances in Applied Mathematics
Vol.06 No.03(2017), Article ID:20671,10
pages
10.12677/AAM.2017.63030
Higher Order Iterative Operator Splitting Method for the 2D Convection Diffusion Equation with Variable Coefficients
Lin Yao, Haiyan Su
College of Mathematics and System Sciences, Xinjiang University, Urumqi Xinjiang

Received: May 3rd, 2017; accepted: May 18th, 2017; published: May 25th, 2017

ABSTRACT
In this paper, a novel higher order iterative operator splitting method is presented for the 2D convection diffusion equation with the variable coefficient. The proposed scheme combines the classical iterative scheme and Zassenhaus product formula for the temporal discretization. And Fourier pseudo spectral method and dimensional splitting scheme are applied for the spatial operators. The numerical results verified that the proposed method can get second order accuracy by weighted iterative scheme. Besides, the new method not only can reduce numerical error but also save a lot of CPU time than the classical iterative method.
Keywords:Convection Diffusion, Zassenhaus Product, Higher Order Iterative, Fourier Pseudo Spectral
变系数2D对流扩散方程的高阶迭代算子 分裂方法
姚林,苏海燕
新疆大学数学与系统科学学院,新疆 乌鲁木齐
收稿日期:2017年5月3日;录用日期:2017年5月18日;发布日期:2017年5月25日

摘 要
本文针对变系数2D对流扩散方程,呈现了一种新颖的高阶迭代算子分裂方法。该方法结合了经典迭代格式和Zassenhaus乘积公式。傅立叶谱方法和维数分裂格式用于空间算子。数值实验验证了所提出的方法通过加权方法可以达到高阶精度。此外,新方法不仅可以减少误差而且能够节省大量的CPU时间。
关键词 :对流扩散,Zassenhaus乘积,高阶迭代,傅立叶拟谱

Copyright © 2017 by authors and Hans Publishers Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/


1. 引言
众所周知,许多复杂有趣的现象是由于对流扩散方程中的对流项和扩散项的不同引起的。因此,它的数值解的研究在许多科学和工程领域中都具有重要的意义,呈现于 [1] [2] [3] 。因为扩散项和对流项的特点,很难找到一个精确有效的数值方法。因此,求解对流扩散问题的有效数值解方法是计算数学中的一个重要研究课题。已有的数值方法有限差分方法 [4] ,有限体积方法 [5] 和有限元方法 [6] 。然而,对于对流占优的问题,通常的有限差分法和有限元法解对流占优的问题可能会产生数值震荡。本文提出的新方法能够很好地消除震荡。
本文将考虑变系数对流扩散方程:
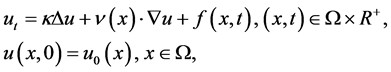 (1)
(1)
这地方 是一个在
是一个在 上的有界区域,
上的有界区域,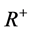 是在
是在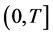 上的时间范围,
上的时间范围,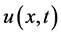 表示浓度,
表示浓度,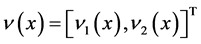 表示速度场,
表示速度场,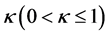 是扩散系数,
是扩散系数,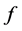 是有界的连续函数。本文将使用周期性边界条件处理对流扩散方程。
是有界的连续函数。本文将使用周期性边界条件处理对流扩散方程。
Jürgen Geiser研究了常系数对流扩散方程,使用改进的加权迭代格式,得到了很好的结果,呈现于 [7] [8] 。本文研究的高阶迭代格式也是改进的经典迭代格式基于Zassenhaus 乘积公式。主要的思想是应用Zassenhaus 乘积公式不断改进迭代格式的初始条件,从而提高经典迭代格式的精度和节省CPU时间。经典迭代格式的基本思想是把复杂的物理问题分解成简单的物理问题,从而能够简化运算和并行计算,看 [9] [10] 。Zassenhaus乘积公式是李代数中的一个基本的重要的公式。
本文将应用加权方法求解变系数的二维对流扩散方程。空间离散应用傅立叶谱方法,时间离散使用加权迭代格式和高阶龙格库塔技术。更具体地,我们使用维数分裂的思想把高维问题分成几个简单的低维问题,使求解变得简单,本文的维数分裂格式是沿着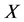 方向的算子和沿
方向的算子和沿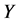 方向的算子。然后使用高阶迭代格式和高阶龙格库塔方法去解低维问题,可以减少分裂误差和促进解的过程。另外,提出的新方法要比经典的迭代方法省CPU时间和收敛精度高。
方向的算子。然后使用高阶迭代格式和高阶龙格库塔方法去解低维问题,可以减少分裂误差和促进解的过程。另外,提出的新方法要比经典的迭代方法省CPU时间和收敛精度高。
本文的框架如下:第二部分,介绍迭代算子分裂方法。第三部分,介绍傅立叶拟谱方法和维数分裂格式。第四部分,讨论高阶迭代格式联合经典的迭代格式和Zassenhaus乘积公式。第五部分,几个数值实例验证高阶格式的高效性和收敛率。第六部分,结论。
2. 经典的迭代算子分裂方法
我们知道经典的迭代格式广泛用于解决现实生活中的问题。本文考虑下列的非均匀的柯西问题
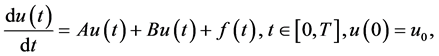
其中 是初始条件,线性算子是在巴拿赫空间
是初始条件,线性算子是在巴拿赫空间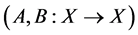
 上的有界线性算子,
上的有界线性算子, 是连续函数。
是连续函数。
算法2.1给出了经典的迭代格式,本文考虑使用交替迭代格式去求解上面的非均匀的柯西问题:
 (2)
(2)
这里初始迭代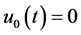 ,其中
,其中 是初始条件,
是初始条件,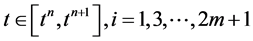 。这个迭代格式的数值解定义为
。这个迭代格式的数值解定义为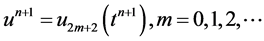 。在下面的章节中,将推导出高阶迭代格式基于交替迭代格式和Zassenhaus乘积公式。
。在下面的章节中,将推导出高阶迭代格式基于交替迭代格式和Zassenhaus乘积公式。
3. 傅立叶谱离散和维数分裂格式
我们应用傅立叶谱方法 [11] 去解方程(3)和(4)。更具体地,给定一个正整数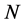 ,使
,使
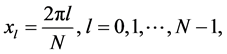
是在区间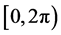 上的等距网格,这些点称为傅立叶谱点。给定一套节点基函数,然后做这套基函数的线性组合,组合系数是节点函数值,有
上的等距网格,这些点称为傅立叶谱点。给定一套节点基函数,然后做这套基函数的线性组合,组合系数是节点函数值,有
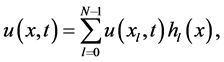
这地方基函数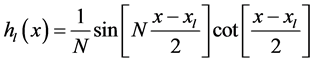 和
和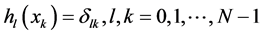 ,
,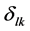 是克罗内克
是克罗内克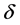 函数。对函数
函数。对函数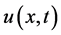 求
求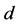 阶导,导函数可以应用谱离散点的线性组合近似逼近,有
阶导,导函数可以应用谱离散点的线性组合近似逼近,有

我们可以把上述公式写成矩阵向量乘积的形式
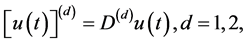
这里
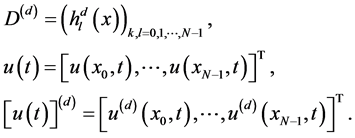
一阶傅立叶微分矩阵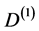 可以写成形式
可以写成形式
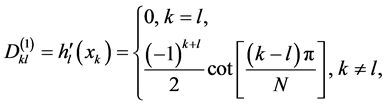
二阶傅立叶微分矩阵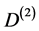 可以写成形式
可以写成形式
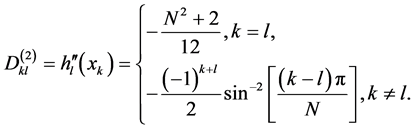
特别地,定义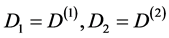 。这样就推导了一维方程的一阶微分矩阵和二阶微分矩阵。下面讨论二维方程的微分矩阵形式。
。这样就推导了一维方程的一阶微分矩阵和二阶微分矩阵。下面讨论二维方程的微分矩阵形式。
对于本文要求解的二维对流扩散方程,首先应用维数分裂处理这个方程,能够得到下列的形式
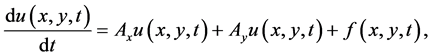
这地方
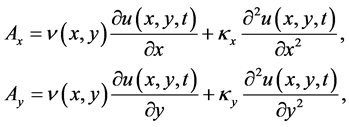
然后使用傅立叶拟谱方法离散空间算子,前面介绍了一维微分矩阵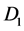 和
和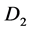 ,对于二维空间算子,使用克罗内克张量积通过一阶微分矩阵
,对于二维空间算子,使用克罗内克张量积通过一阶微分矩阵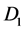 和二阶微分矩阵
和二阶微分矩阵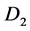 能够得到二维微分矩阵,把偏微分方程转化为常微分方程组,方程形式
能够得到二维微分矩阵,把偏微分方程转化为常微分方程组,方程形式
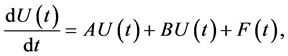 (3)
(3)
这里
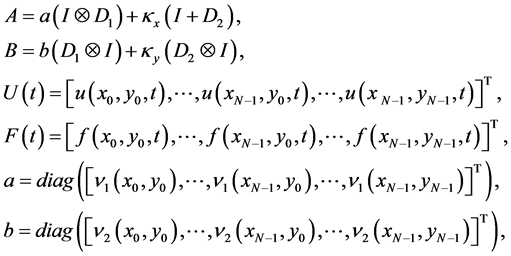
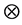 表示克罗内克张量积符号,
表示克罗内克张量积符号,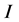 表示单位矩阵。
表示单位矩阵。
在下面的章节中,我们将推导高阶迭代格式和讨论常微分方程组(3)的数值解,理论能够证明本文提出的加权迭代格式可以增强收敛精度和节省CPU时间。
4. 高阶迭代格式用于时间离散
本节将讨论高阶迭代格式基于算法2.1和Zassenhaus乘积公式,构造的高阶方法可以提高收敛率和减少数值误差,以及减少迭代步数,从而节省时间。首先给出算法2.1的分析解
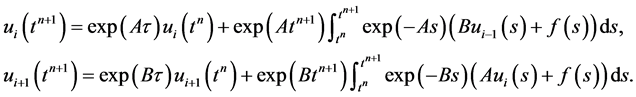 (4)
(4)
我们假设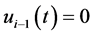 ,因此对于
,因此对于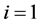 ,有
,有
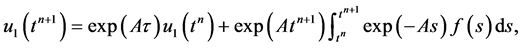 (5)
(5)
这时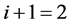 ,得到第二步
,得到第二步
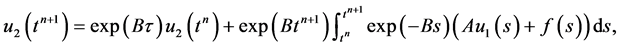 (6)
(6)
这地方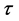 是时间步长,
是时间步长,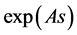 是指数函数。下面推导加权迭代格式。
是指数函数。下面推导加权迭代格式。
我们将应用Zassenhaus乘积公式 [12] ,这个公式具体形式
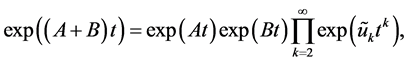
这里,将公式进行泰勒公式展开,能够推导出下列的权的误差阶 [10]
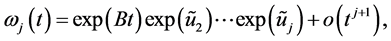
这地方 是Zassenhaus指数。能够推导出Zassenhaus指数为
是Zassenhaus指数。能够推导出Zassenhaus指数为
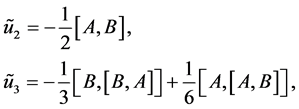
这里[]是李代数括号,我们定义: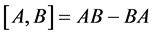 。因此权公式可以表示为
。因此权公式可以表示为
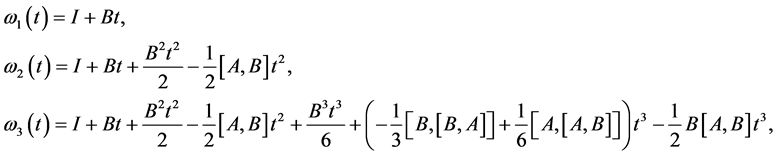
这样就推导出来了权公式。因此对于初始迭代(5)做如下改进

因此迭代格式的误差精度提高到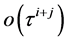 (参见 [13] ),这样每增加一步权,原来经典迭代格式的误差提高一阶。
(参见 [13] ),这样每增加一步权,原来经典迭代格式的误差提高一阶。
一步加权和两步加权迭代格式为
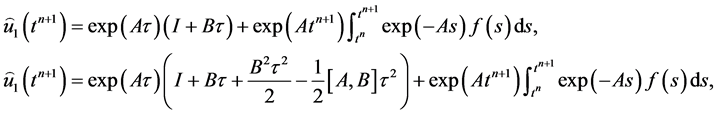
因此加权迭代的误差率能够提高到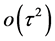 和
和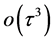 。
。
这个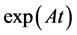 和
和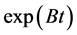 应用Pade'方法近似,积分项使用四阶龙格库塔方法离散,这样能够获得高阶结果。加权迭代格式将通过一些数值实例进行验证。
应用Pade'方法近似,积分项使用四阶龙格库塔方法离散,这样能够获得高阶结果。加权迭代格式将通过一些数值实例进行验证。
5. 数值实验
本章节将验证提出的新格式的收敛阶和CPU时间,以及误差图。
首先给出方程(1)一个真解
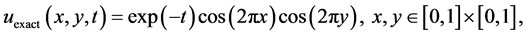
设置终止时间 ,初始条件
,初始条件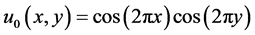 。数值误差使用
。数值误差使用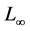 范数形式,定义
范数形式,定义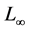 范数
范数
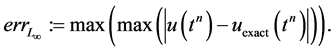
我们将选取不同的对流系数和不同的扩散系数来验证高阶格式的误差阶。
5.1. 数值实例1
在这个数值例子中,考虑一般的对流扩散方程,扩散系数选取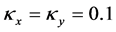 ,表中将给出不同对流系数的情况。
,表中将给出不同对流系数的情况。
表1中呈现的是加权迭代算法的误差,对流系数选取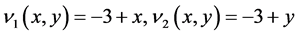 ,选取空间谱点
,选取空间谱点 ,时间步长选取不同的适合的步长。
,时间步长选取不同的适合的步长。
表2将给出该算法误差,空间点选取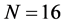 ,对流系数选取
,对流系数选取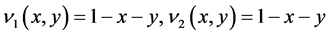 ,挑选和表1中一样的时间步长。
,挑选和表1中一样的时间步长。
表3说明的是加权迭代算法的误差阶,对流系数选择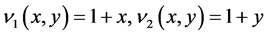 ,空间点仍然选择
,空间点仍然选择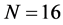 ,时间步长和表2同步。
,时间步长和表2同步。
表4呈现的权迭代算法的CPU时间比较,选择不同的空间点,时间步长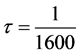 ,对流系数
,对流系数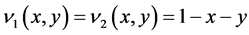 ,比较没有加权,一步加权和两步加权的时间。
,比较没有加权,一步加权和两步加权的时间。
图1呈现的是2步加权的误差图,对流系数选择表1中系数,时间步长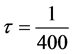 ,空间点
,空间点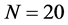 。
。
图2呈现的也是2步加权的误差图,对流系数选择表2中系数,时间步长、空间点和图1中同步。
从表中能够看出,不同的对流系数对权格式的精度是有影响的,对流系数选择的不好可能会导致2步加权的误差增大,从时间的比较中也能看出,加权方法耗费的时间并不是很多相比于没有加权,但误差减小了很多,说明加权方法是一种花费时间少,且精度高的方法。从图中能够看出不同的对流系数呈现的误差图也不一样,选择对流系数函数值无零点的对流系数,误差图的跳跃性就不会很大,明显看出图1比图2好。
5.2. 数值实例2
在这个例子中,将考虑对流占优的情形,选取扩散系数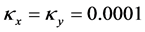 ,表中同样给出不同的对流系数来验证加权方法的误差阶情况。
,表中同样给出不同的对流系数来验证加权方法的误差阶情况。
表5呈现的是加权迭代的误差比较,对流系数选取表1中的对流系数,空间点选择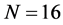 ,时间步长同样选择表1中的步长。
,时间步长同样选择表1中的步长。
表6表明的是加权格式的误差阶比较,对流系数选择表2中的对流系数,空间谱离散点选择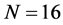 ,时间步长和上表同步。
,时间步长和上表同步。
表7呈现的是高阶迭代方法的误差比较,对流系数选择表3中的系数,空间点和时间步长和表6同步。
图3呈现的是2步加权的误差图,对流系数、时间步长和空间点和图1同步。
图4表明的是2步加权的误差图,对流系数、时间步长和空间点和图2同步。
从表中可以看出,对于对角占优的对流扩散问题,加权迭代方法计算的比较好,同样体现了随着扩散系数的减小,误差会增大。同样也验证了加权方法的精度高,节省时间。从误差图中可以看出,图4的跳跃性相比图2更大,说明强对角占优凸显了双曲方程的特征,跳动性比较大,这样会影响高阶格式收敛性和稳定性。但不会影响加权方法的精度。
表1. 加权迭代数值误差比较。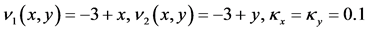
表2. 加权格式误差比较。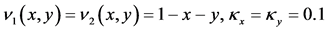
表3. 加权迭代数值误差比较。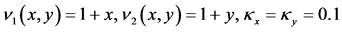
表4. 加权迭代的CPU时间比较。
表5. 加权迭代误差比较。
表6. 加权格式误差比较。
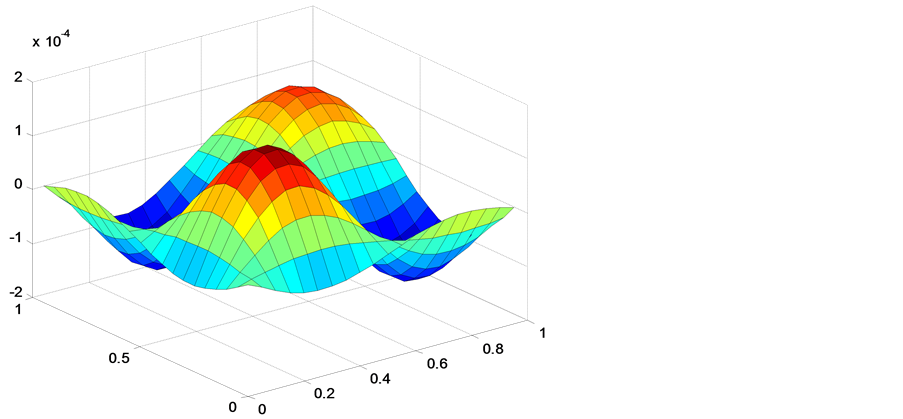
Figure 1. Error chart. 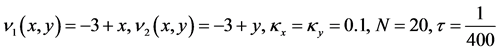
图1. 误差图。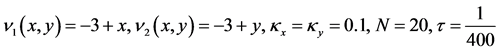
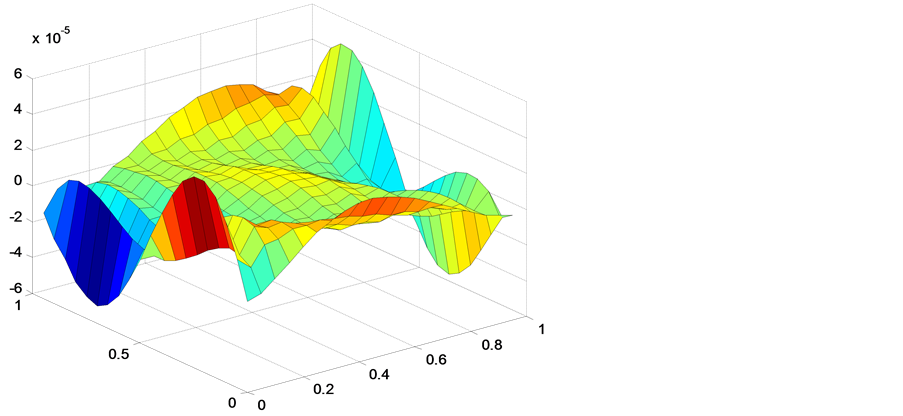
Figure 2. Error chart. 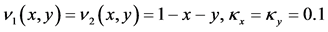
图2. 误差图。
表7. 加权迭代数值误差比较。
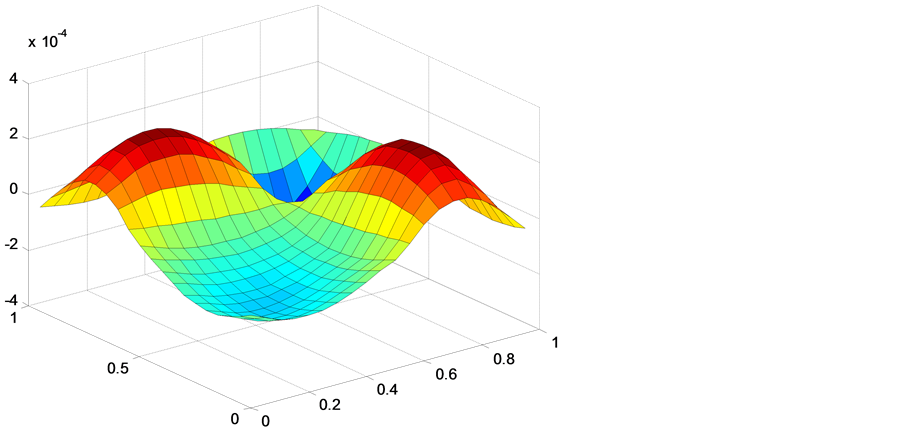
Figure 3. Error chart. 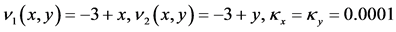
图3. 误差图。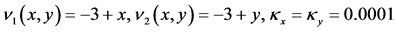

Figure 4. Error chart. 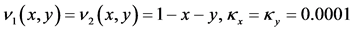
图4. 误差图。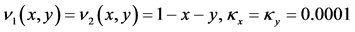
6. 结论
本文呈现了一种高阶迭代格式对于求解变系数2D对流扩散方程。提出的新方法结合了经典迭代格式和Zassenhaus乘积公式。傅立叶谱离散技术和维数分裂方法用于空间算子。数值算例呈现了新方法的高精度和高效性。
基金项目
国家自然科学基金资助项目(11271313)。
文章引用
姚林,苏海燕. 变系数2D对流扩散方程的高阶迭代算子分裂方法
Higher Order Iterative Operator Splitting Method for the 2D Convection Diffusion Equation with Variable Coefficients[J]. 应用数学进展, 2017, 06(03): 249-258. http://dx.doi.org/10.12677/AAM.2017.63030
参考文献 (References)
- 1. 章本照, 印建安, 张宏基. 流体力学数值方法[M]. 北京: 机械工业出版社, 2003
- 2. 李荣华, 刘播. 微分方程数值解法[M]. 第四版. 北京: 高等教育出版社, 2009.
- 3. Li, Q., Chai, Z. and Shi, B. (2014) An Efficient Lattice Boltzmann Model for Steady Convection Diffusion Equation. Journal of Scientific Computing, 61, 308-326. https://doi.org/10.1007/s10915-014-9827-z
- 4. Galligani, E. (2013) A Nonlinearity Lagging for the Solution of Nonlinear Steady State Reaction Diffusion Problems. Communications in Nonlinear Science and Numerical Simulation, 18, 567-583.
- 5. Angelini, O. and Brenner, K. (2013) A Finite Volume Method on General Meshes for a Degenerate Parabolic Convection Reaction Diffusion Equation. Numerische Mathematik, 123, 219-257. https://doi.org/10.1007/s00211-012-0485-5
- 6. Bause, M. and Schwegler, K. (2013) Higher Order Finite Element Approximation of Systems of the Convection Diffusion Reaction Equations with Small Diffusion. Journal of Computational and Applied Mathematics, 246, 52-64.
- 7. Geiser, J. and Tanoglu, G. (2011) Operator-Splitting Methods via the Zassenhaus Product Formula. Applied Mathematics and Computation, 217, 4557-4575.
- 8. Csomós, P. and Faragó, I. (2005) The Weighted Sequential Splitting and Their Analysis. Computers and Mathematics with Applications, 50, 1017-1031.
- 9. Geiser, J. (2008) Iterative Operator-Splitting Methods with Higher-Order Time Integration Methods and Applications for Parabolic Partial Differential Equations. Journal of Computational Applied Mathematics, 217, 227-242. https://doi.org/10.1002/num.20568
- 10. Geiser, J. (2011) Iterative Operator-Splitting Methods for the Nonlinear Differential Equations and Applications. Numerical Method for Partial Differential Equation, 27, 1026-1054.
- 11. Shen, J., Tang, T. and Wang, L. (2011) Spectral Methods. Springer, Berlin Heidelberg. https://doi.org/10.1007/978-3-540-71041-7
- 12. Scholz, D. (2006) A Note on the Zassenhaus Product Formula. Journal of Mathematical Physics, 47, 373-418. https://doi.org/10.1063/1.2178586
- 13. Geiser, J. and Tano, G. (2011) Higher Order Operator Splitting Methods via the Zassenhaus Product Formula: Theory and Application. Computer and Mathematic with Application, 62, 1994-2015.
