度和与边数条件下过线性森林圈的一些研究 Researches on the Cycles through Linear Forest under the Conditions of Degree Sum and Edge Number

doi:10.12677/AAM.2023.121005

Advances in Applied Mathematics
Vol. 12 No. 01 ( 2023 ), Article ID: 60263 , 8 pages
10.12677/AAM.2023.121005

度和与边数条件下过线性森林圈的一些研究

邵雅欣，杨卫华^*

●How to Cite this Article

太原理工大学数学学院，山西太原

收稿日期：2022年12月12日；录用日期：2023年1月5日；发布日期：2023年1月13日

摘要

2009年，Faudree提出在给定的 $σ_{2} (G)$ 条件下，图G过 $(k, t)$ -线性森林的 $(k, t, 2 t + k)$ -泛圈问题。本文证明了在该 $σ_{2} (G)$ 条件下，对任意 $r \in [m a x {4, k + 2 t}, n]$ ，G中存在长为r或 $r + 1$ 的圈过 $(k, t)$ -线性森林。此外，本文还给出了图G是 $(k, t)$ -哈密顿的一个边数条件。

关键词

线性森林，哈密顿圈，泛圈

Researches on the Cycles through Linear Forest under the Conditions of Degree Sum and Edge Number

Yaxin Shao, Weihua Yang^*

College of Mathematics, Taiyuan University of Technology, Taiyuan Shanxi

Received: Dec. 12^th, 2022; accepted: Jan. 5^th, 2023; published: Jan. 13^th, 2023

ABSTRACT

In 2009, Faudree proposed the $(k, t, 2 t + k)$ -pancyclic problem of graph G passing through $(k, t)$ -linear forest under given $σ_{2} (G)$ condition. In this paper, we prove that under the $σ_{2} (G)$ condition, for any $r \in [m a x {4, k + 2 t}, n]$ , there exists a cycle passing through $(k, t)$ -linear forest of length r or $r + 1$ in the graph G. In addition, an edge number condition that graph G is $(k, t)$ -Hamiltonian is given.

Keywords:Linear Forest, Hamiltonian Cycle, Pancyclic

This work is licensed under the Creative Commons Attribution International License (CC BY 4.0).

http://creativecommons.org/licenses/by/4.0/

1. 引言

本文只考虑无自环和重边的简单图。下面先给出一些基本的定义和符号， $V (G)$ ， $E (G)$ 和 $δ (G)$ 分别表示图G的点集、边集和最小度；图G的点数 $| V (G) |$ 记为n，边数 $| E (G) |$ 记为m， $d_{G} (u)$ 表示图G中点u的度数。对于一个非完全图G，定义 $σ_{2} (G) = \min {d_{G} (u_{1}) + d_{G} (u_{2})}$ ，其中 $u_{1}$ 、 $u_{2}$ 是任意两个不相邻点对。图G中包含了所有点的圈称为哈密顿圈，一个存在哈密顿圈的图称为哈密顿图。一个 $(k, t, s)$ -线性森林是一个由k条边、t条路构成的线性森林，且t条路中有s条单点路。当一个线性森林F中单点路的数量未知时，简称F为 $(k, t)$ -线性森林。如果对于G中的任意 $(k, t)$ -线性森林F，G中都存在一个哈密顿圈包含F，那么称G是 $(k, t)$ -哈密顿的。给定整数m和n ( $k + t \leq m \leq n$ )，如果对于任意的 $(k, t)$ -线性森林及任意的整数 $r (m \leq r \leq n)$ ，G中都存在长度为r的圈包含这个线性森林，那么称G是 $(k, t, m)$ -泛圈的。本文未定义的术语可参考文献 [1]。

1952年，Dirac [2] 给出：设G是一个阶数 $n \geq 3$ 的图，如果最小度 $δ (G) \geq n / 2$ ，那么G是哈密顿的。1960年，Ore [3] 把上述结论推广到不相邻两点度和条件下哈密顿圈存在的结果：设G是一个阶数 $n \geq 3$ 的图，如果 $σ_{2} (G) \geq n$ ，那么G是哈密顿的。在此基础上，Kronk [4] 研究了过k-路的圈，并分别给出了不相邻两点度和条件和边数条件下的结论：设G是一个n阶图且满足 $σ_{2} (G) \geq n + k$ 或满足边数 $m \geq (n - 1) (n - 2) / 2 + k + 2$ ，那么G是k-路哈密顿的。Faudree [5] 等人把过k-路的圈推广到过 $(k, t)$ -线性森林的情况。

定理1 [5] 令G是一个n阶图，k，t和n是正整数且满足 $2 \leq k + t \leq n$ ，F是一个 $(k, t)$ -线性森林。如果

(i) $σ_{2} (G) \geq n + k$ ，当 $F = P_{k + 1} \cup (t - 1) K_{1}$ 时，

(ii) $σ_{2} (G) \geq n + k - ε (n, k)$ ，其他情况，

那么G是 $(k, t)$ -哈密顿的，其中 $2 | (n - k)$ 时 $ε (n, k) = 1$ ，否则 $ε (n, k) = 0$ 。此外， $σ_{2} (G)$ 的条件是紧的。

除了研究哈密顿圈外， [5] 还研究了泛圈性的结果，并提出一个改进度和条件下的问题。

定理2 [5] 令G是一个n阶图，k，t和n是正整数且满足 $2 \leq k + t \leq n$ ，F是一个 $(k, t)$ -线性森林。如果 $σ_{2} (G) \geq n + k$ ，那么G是 $(k, t, 2 t + k)$ -泛圈的。

问题 [5] 令G是一个n阶图，k，t和n是正整数且满足 $2 \leq k + t \leq n$ ，F是一个 $(k, t)$ -线性森林。如果

(i) $σ_{2} (G) \geq n + k$ ，当 $P_{k + 1} \subseteq F$ 时，

(ii) $σ_{2} (G) \geq n + k - ε (n, k)$ ，其他情况，

那么G是 $(k, t, 2 t + k)$ -泛圈的吗？

何剑在 [6] 中尝试解决上述问题，给出了在 $(k, t, 0)$ -线性森林的情况下一个结果。本文基于Faudree等人提出的上述问题猜想，将 [6] 中的结论推广到 $(k, t)$ -线性森林的情况，即线性森林中可以有单点路。此外，本文还给出了图G是 $(k, t)$ -哈密顿的一个边数条件。

2. 主要结果

本文证明了以下结果：

定理3 设k，t和n是正整数，满足 $2 \leq k + t \leq n$ ，G是n阶图，F是 $(k, t)$ -线性森林，如果

(i) $σ_{2} (G) \geq n + k$ ，当 $F = P_{k + 1} \cup (t - 1) K_{1}$ ，

(ii) $σ_{2} (G) \geq n + k - ε (n, k)$ ，其他情况，

则对任意 $r \in [\max {4, k + 2 t}, n]$ ，G中存在长为r或 $r + 1$ 的圈过F。

定理4 设k，t和n是正整数，满足 $2 \leq k + t \leq n$ ，G是n阶图，F是 $(k, t)$ -线性森林，如果边数

(i) $m \geq (n - 1) (n - 2) / 2 + k + 2$ ，当 $F = P_{k + 1} \cup (t - 1) K_{1}$ 时，

(ii) $m \geq (n - 1) (n - 2) / 2 + k + 2 - ε (n, k)$ ，其他情况，

那么G是 $(k, t)$ -哈密顿的，其中 $2 | (n - k)$ 时 $ε (n, k) = 1$ ，否则 $ε (n, k) = 0$ 。

3. 证明

首先给出证明过程中需要用到的两个引理。

引理6 [6] 设 $k = t = 1$ ，G是阶 $n \geq k + t$ 的图，F是G中 $(k, t, t - k)$ -线性森林。如果 $σ_{2} (G) \geq n + k$ ，则G中存在过F的长度不大于4的圈。

引理7 [6] 设G是阶 $n \geq k + t$ 的图，其中k，t为满足 $k \leq t$ 的正整数。设F是G中 $(k, t, t - k)$ -线性森林。如果

(i) $σ_{2} (G) \geq n + k$ ， $k = 1$ 时，

(ii) $σ_{2} (G) \geq n + k - ε (n, k)$ ， $k \geq 2$ 时，

则当 $t \geq 2$ 时，G存在过F的圈C，使得 $C - V (F)$ 为孤立点图或空图。

在证明定理3前还需要给出两个定理来辅助证明。

定理8 设G是阶 $n \geq k + t$ 的图，其中k，t为满足 $k \leq t$ 的正整数。设F是G中 $(k, t, t - k)$ -线性森林。如果G中存在长度为 $r \leq n - 1$ 的过F的圈，并且

(i) $σ_{2} (G) \geq n + k$ ， $k = 1$ 时，

(ii) $σ_{2} (G) \geq n + k - ε (n, k)$ ， $k \geq 2$ 时，

则G中存在长为 $r + 1$ 或 $r + 2$ 的圈过F。

证明假设图G中不存在过F的长度为 $r + 1$ 或 $r + 2$ 的圈。已知G中存在长为 $r \leq n - 1$ 的过F的圈，记为 $C_{0} = v_{1} v_{2} \dots v_{r} v_{1}$ ，那么有 $H_{0} = G - C_{0} \neq \emptyset$ 。因为 $σ_{2} (G) \geq n + k - 1$ ，所以G是 $k + 1$ -连通图，不妨设 $v_{1} z$ 是连接 $C_{0}$ 和 $H_{0}$ 的边，且有 $v_{1} v_{2} \notin E (F)$ 。那么 $v_{2} z \notin E (G)$ ，且 $N (v_{2}) \cap N (z) \subseteq V (C_{0})$ ，否则G中就存在过F的长度为 $r + 1$ 或 $r + 2$ 的圈。故而 $P_{0} = v_{2} v_{3} \dots v_{r} v_{1} z$ 是G中过F的且长度为r的路。

设 $P = u_{1} u_{2} \dots u_{r + 1}$ 是G中一条长为r的路，且满足

(I) $E (F) \subseteq E (P)$ ， $V (F) \subseteq V (P)$ ， $u_{r + 1} \notin V (F)$ ，

(II) 在(I)的前提下， $| {u_{1} u_{2}} \cap E (F) |$ 最大。

由前边的分析知， $P_{0} = v_{2} v_{3} \dots v_{r} v_{1} z$ 是G中满足条件(I)的路，因此假设中选择的路P是存在的。

如果 $u_{1} u_{r + 1} \in E (G)$ ，那么G中存在长为 $r + 1$ 的圈 $u_{1} u_{2} \dots u_{r + 1} u_{1}$ 过F；如果 $u_{1}$ ， $u_{r + 1}$ 在 $H = G - V (P)$ 中有公共邻点z，那么G中存在长为 $r + 2$ 的圈 $u_{1} u_{2} \dots u_{r + 1} z u_{1}$ 过F。故而假设 $u_{1} u_{r + 1} \notin E (G)$ 且 $N_{H} (u_{1}) \cap N_{H} (u_{r + 1}) = \emptyset$ 。因此， $d_{H} (u_{1}) + d_{H} (u_{r + 1}) \leq | H | = n - r - 1$ 。

令 $X = {j | 1 \leq j \leq r, u_{1} u_{j + 1} \in E (G)}$ ， $Y = {j | 1 \leq j \leq r, u_{j} u_{r + 1} \in E (G)}$ ，则 $X \cap Y \subseteq {j | u_{j} u_{j + 1} \in E (F)}$ ，否则 $\exists j \in X \cap Y$ 使得 $u_{1} u_{j + 1}, u_{j} u_{r + 1} \in E (G)$ ， $u_{j} u_{j + 1} \notin E (F)$ ，那么圈 $u_{1} u_{2} \dots u_{j} u_{r + 1} u_{r} \dots u_{j + 1} u_{1}$ 过F且长度为 $r + 1$ (如图1)。

Figure 1. Schematic diagram of cycle $u_{1} u_{2} \dots u_{j} u_{r + 1} u_{r} \dots u_{j + 1} u_{1}$

图1. 存在圈 $u_{1} u_{2} \dots u_{j} u_{r + 1} u_{r} \dots u_{j + 1} u_{1}$ 的示意图

于是， $d_{P} (u_{1}) + d_{P} (u_{r + 1}) = | X | + | Y | = | X \cup Y | + | X \cap Y | \leq | [1, r] | + | E (F) | = r + k$ ，故得 $d_{G} (u_{1}) + d_{G} (u_{r + 1}) = d_{H} (u_{1}) + d_{P} (u_{1}) + d_{H} (u_{r + 1}) + d_{P} (u_{r + 1}) \leq n + k - 1$ 。

(i) $k = 1$ 时， $σ_{2} (G) \geq n + k$ ，矛盾。

(ii) $k \geq 2$ 时， $σ_{2} (G) \geq n + k - ε (n, k)$ ，故而 $ε (n, k) = 1$ ，从而有 $d_{G} (u_{1}) + d_{G} (u_{r + 1}) = n + k - 1$ ，同时 $| X \cup Y | = | [1, r] |$ ， $| X \cap Y | = | E (F) |$ 。

如果 $u_{1} u_{2} \in E (F)$ ，则 $1 \in X \cap Y$ ，那么 $u_{1} u_{r + 1} \in E (G)$ ，与先前的假设矛盾。也就是说对于任何满足(I)的路 $P = u_{1} u_{2} \dots u_{r + 1}$ 都有 $u_{1} u_{2} \notin E (F)$ 。类似地，也有 $u_{r} u_{r + 1} \notin E (F)$ 。

设 $u_{i} u_{i + 1}$ 和 $u_{j} u_{j + 1}$ 是P上两条不被其他F-边间隔的F-边， $u_{s}$ 是 $P (u_{i + 1}, u_{j}]$ 的第一个F中的孤立点且 $u_{j + 2} \notin V (F)$ 。由 $| X \cap Y | = | E (F) |$ 有， $i, j \in X \cap Y$ ，从而有 $u_{i + 1}, u_{j + 1} \in N (u_{1})$ ， $u_{i}, u_{j} \in N (u_{r + 1})$ 。

下面先考虑s的取值，首先有 $s \neq j$ 。若 $s = j$ ，那么存在路 $u_{i + 1} u_{i} \dots u_{1} u_{j + 1} u_{s} u_{r + 1} u_{r} \dots u_{j + 2}$ 与P的选取矛盾(如图2)。

Figure 2. Schematic diagram of path $u_{i + 1} u_{i} \dots u_{1} u_{j + 1} u_{s} u_{r + 1} u_{r} \dots u_{j + 2}$

图2. 存在路 $u_{i + 1} u_{i} \dots u_{1} u_{j + 1} u_{s} u_{r + 1} u_{r} \dots u_{j + 2}$ 的示意图

如果 $s \neq i + 2$ ，则 $s \geq i + 3$ ，那么 $P (u_{i + 1}, u_{s})$ 内存在点 $u_{i + 2}$ 。由 $| X \cup Y | = | [1, r] |$ 可知， $u_{i + 2} \in N (u_{1})$ 或 $u_{i + 2} \in N (u_{r + 1})$ ，但上述两条件不同时成立，否则与之前的假设矛盾。当 $u_{i + 2} \in N (u_{1})$ 时，路 $u_{i + 1} u_{i} \dots u_{1} u_{i + 2} u_{i + 3} \dots u_{r + 1}$ 与P的选取矛盾(如图3)。

Figure 3. Schematic diagram of path $u_{i + 1} u_{i} \dots u_{1} u_{i + 2} u_{i + 3} \dots u_{r + 1}$

图3. 存在路 $u_{i + 1} u_{i} \dots u_{1} u_{i + 2} u_{i + 3} \dots u_{r + 1}$ 的示意图

当 $u_{i + 2} \in N (u_{r + 1})$ 时，路 $u_{i + 1} u_{i} \dots u_{1} u_{j + 1} u_{j} \dots u_{s} u_{i + 2} u_{r + 1} u_{r} \dots u_{j + 2}$ 与P的选取矛盾(如图4)。因此 $s = i + 2$ 。

Figure 4. Schematic diagram of path $u_{i + 1} u_{i} \dots u_{1} u_{j + 1} u_{j} \dots u_{s} u_{i + 2} u_{r + 1} u_{r} \dots u_{j + 2}$

图4. 存在路 $u_{i + 1} u_{i} \dots u_{1} u_{j + 1} u_{j} \dots u_{s} u_{i + 2} u_{r + 1} u_{r} \dots u_{j + 2}$ 的示意图

如果 $u_{1} u_{s} \in E (G)$ ，则路 $u_{i + 1} u_{i} \dots u_{1} u_{s} u_{i + 3} \dots u_{r + 1}$ 与P的选取矛盾(如图3)。因此， $u_{1} u_{s} \notin E (G)$ 。如果 $u_{s} u_{r + 1} \in E (G)$ ，则路 $u_{i + 1} u_{i} \dots u_{1} u_{j + 1} u_{j} \dots u_{s} u_{r + 1} u_{r} \dots u_{j + 2}$ 与P的选取矛盾(如图5)。因此， $u_{s} u_{r + 1} \notin E (G)$ 。

Figure 5. Schematic diagram of path $u_{i + 1} u_{i} \dots u_{1} u_{j + 1} u_{j} \dots u_{s} u_{r + 1} u_{r} \dots u_{j + 2}$

图5. 存在路 $u_{i + 1} u_{i} \dots u_{1} u_{j + 1} u_{j} \dots u_{s} u_{r + 1} u_{r} \dots u_{j + 2}$ 的示意图

此外，有 $N_{H} (u_{1}) \cap N_{H} (u_{s}) = \emptyset$ ，否则 $\exists z \in N_{H} (u_{1}) \cap N_{H} (u_{s})$ ，又因为 $u_{r + 1} \notin V (F)$ ，故而存在路 $u_{i + 1} u_{i} \dots u_{1} z u_{s} u_{s + 1} \dots u_{r}$ 与P的选取矛盾(如图6)。

Figure 6. Schematic diagram of path $u_{i + 1} u_{i} \dots u_{1} z u_{s} u_{s + 1} \dots u_{r}$

图6. 存在路 $u_{i + 1} u_{i} \dots u_{1} z u_{s} u_{s + 1} \dots u_{r}$ 的示意图

也有 $N_{H} (u_{s}) \cap N_{H} (u_{r + 1}) = \emptyset$ ，否则 $\exists y \in N_{H} (u_{s}) \cap N_{H} (u_{r + 1})$ ，当 $r = j + 1$ 时，路 $u_{i + 1} u_{i} \dots u_{1} u_{j + 1} u_{j} \dots u_{s} y$ 与P的选取矛盾(如图7)；当 $r \geq j + 2$ 时，路 $u_{i + 1} u_{i} \dots u_{1} u_{j + 1} u_{j} \dots u_{s} y u_{r + 1} u_{r} \dots u_{j + 3}$ 与P的选取矛盾(如图8)。

Figure 7. Schematic diagram of path $u_{i + 1} u_{i} \dots u_{1} u_{j + 1} u_{j} \dots u_{s} y$

图7. 存在路 $u_{i + 1} u_{i} \dots u_{1} u_{j + 1} u_{j} \dots u_{s} y$ 的示意图

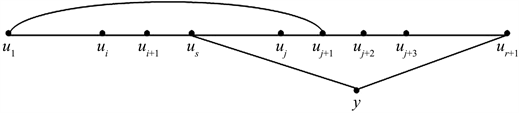
Figure 8. Schematic diagram of path $u_{i + 1} u_{i} \dots u_{1} u_{j + 1} u_{j} \dots u_{s} y u_{r + 1} u_{r} \dots u_{j + 3}$

图8. 存在路 $u_{i + 1} u_{i} \dots u_{1} u_{j + 1} u_{j} \dots u_{s} y u_{r + 1} u_{r} \dots u_{j + 3}$ 的示意图

故而有， $d_{H} (u_{1}) + d_{H} (u_{s}) \leq n - r - 1$ ， $d_{H} (u_{s}) + d_{H} (u_{r + 1}) \leq n - r - 1$ 。

令 $P_{1} = u_{1} u_{2} \dots u_{i + 1}$ ， $P_{2} = u_{i + 2} u_{i + 3} \dots u_{r + 1}$ 。

令 $X_{1} = {l | 1 \leq l \leq i, u_{1} u_{l + 1} \in E (G)}$ ， $Y_{1} = {l | 2 \leq l \leq i + 1, u_{l} u_{s} \in E (G)}$ ，则 $X_{1} \cap Y_{1} \subseteq {l | 2 \leq l \leq i, u_{l} u_{l + 1} \in E (F)} = I_{1}$ ，否则 $\exists l \in X_{1} \cap Y_{1}$ 使得 $u_{1} u_{l + 1}, u_{l} u_{s} \in E (G)$ ， $u_{l} u_{l + 1} \notin E (F)$ ，那么路 $u_{i + 1} u_{i} \dots u_{l + 1} u_{1} u_{2} \dots u_{l} u_{s} u_{i + 3} \dots u_{r + 1}$ 与P的选取矛盾(如图9)。

Figure 9. Schematic diagram of path $u_{i + 1} u_{i} \dots u_{l + 1} u_{1} u_{2} \dots u_{l} u_{s} u_{i + 3} \dots u_{r + 1}$

图9. 存在路 $u_{i + 1} u_{i} \dots u_{l + 1} u_{1} u_{2} \dots u_{l} u_{s} u_{i + 3} \dots u_{r + 1}$ 的示意图

从而有， $d_{P_{1}} (u_{1}) + d_{P_{1}} (u_{s}) \leq | X_{1} \cup Y_{1} | + | X_{1} \cap Y_{1} | \leq | V (P_{1}) | + | I_{1} |$ 。

令 $X_{2} = {l | i + 2 \leq l \leq r - 1, u_{1} u_{l} \in E (G)}$ ， $Y_{2} = {l | i + 2 \leq l \leq r, u_{s} u_{l + 1} \in E (G)}$ ，则 $X_{2} \cap Y_{2} \subseteq {l | i + 2 \leq l \leq r - 1, u_{l} u_{l + 1} \in E (F)} = I_{2}$ ，否则 $\exists l \in X_{2} \cap Y_{2}$ 使得 $u_{1} u_{l}, u_{s} u_{l + 1} \in E (G)$ ， $u_{l} u_{l + 1} \notin E (F)$ ，那么路 $u_{i + 1} u_{i} \dots u_{1} u_{l} u_{l - 1} \dots u_{s} u_{l + 1} u_{l + 2} u_{r + 1}$ 与P的选取矛盾(如图10)。

Figure 10. Schematic diagram of path $u_{i + 1} u_{i} \dots u_{1} u_{l} u_{l - 1} \dots u_{s} u_{l + 1} u_{l + 2} u_{r + 1}$

图10. 存在路 $u_{i + 1} u_{i} \dots u_{1} u_{l} u_{l - 1} \dots u_{s} u_{l + 1} u_{l + 2} u_{r + 1}$ 的示意图

从而有， $d_{P_{2}} (u_{1}) + d_{P_{2}} (u_{s}) \leq | X_{2} \cup Y_{2} | + | X_{2} \cap Y_{2} | \leq | V (P_{2}) | - 1 + | I_{2} |$ 。

因此， $d_{P} (u_{1}) + d_{P} (u_{s}) \leq | V (P) | - 1 + | E (F) | = r + k$ 。

令 $X_{3} = {l | 1 \leq l \leq i, u_{s} u_{l + 1} \in E (G)}$ ， $Y_{3} = {l | 2 \leq l \leq i + 1, u_{l} u_{r + 1} \in E (G)}$ ，则 $X_{3} \cap Y_{3} \subseteq {l | 2 \leq l \leq i, u_{l} u_{l + 1} \in E (F)} = I_{3}$ ，否则 $\exists l \in X_{3} \cap Y_{3}$ 使得 $u_{l + 1} u_{s}, u_{l} u_{r + 1} \in E (G)$ ， $u_{l} u_{l + 1} \notin E (F)$ ，那么路 $u_{i + 1} u_{i} \dots u_{l + 1} u_{s} u_{i + 3} \dots u_{r + 1} u_{l} u_{l - 1} \dots u_{1}$ 与P的选取矛盾(如图11)。

Figure 11. Schematic diagram of path $u_{i + 1} u_{i} \dots u_{l + 1} u_{s} u_{i + 3} \dots u_{r + 1} u_{l} u_{l - 1} \dots u_{1}$

图11. 存在路 $u_{i + 1} u_{i} \dots u_{l + 1} u_{s} u_{i + 3} \dots u_{r + 1} u_{l} u_{l - 1} \dots u_{1}$ 的示意图

从而有， $d_{P_{1}} (u_{s}) + d_{P_{1}} (u_{r + 1}) \leq | X_{3} \cup Y_{3} | + | X_{3} \cap Y_{3} | \leq | V (P_{1}) | + | I_{3} |$ 。

令 $X_{4} = {l | i + 2 \leq l \leq r - 1, u_{s} u_{l + 1} \in E (G)}$ ， $Y_{4} = {l | i + 3 \leq l \leq r, u_{l} u_{r + 1} \in E (G)}$ ，则 $X_{4} \cap Y_{4} \subseteq {l | i + 3 \leq l \leq r - 1, u_{l} u_{l + 1} \in E (F)} = I_{4}$ ，否则 $\exists l \in X_{4} \cap Y_{4}$ 使得 $u_{l + 1} u_{s}, u_{l} u_{r + 1} \in E (G)$ ， $u_{l} u_{l + 1} \notin E (F)$ ，那么当 $j + 1 < l$ 时，路 $u_{i + 1} u_{i} \dots u_{1} u_{j + 1} u_{j + 2} \dots u_{l} u_{r + 1} u_{r} \dots u_{l + 1} u_{s} u_{s + 1} \dots u_{j}$ 与P的选取矛盾(如图12)。当 $j + 1 > l + 1$ 时，路 $u_{i + 1} u_{i} \dots u_{1} u_{j + 1} u_{j} \dots u_{l + 1} u_{s} u_{s + 1} \dots u_{l} u_{r + 1} u_{r} \dots u_{j + 2}$ 与P的选取矛盾(如图13)。

Figure 12. Schematic diagram of path $u_{i + 1} u_{i} \dots u_{1} u_{j + 1} u_{j + 2} \dots u_{l} u_{r + 1} u_{r} \dots u_{l + 1} u_{s} u_{s + 1} \dots u_{j}$

图12. 存在路 $u_{i + 1} u_{i} \dots u_{1} u_{j + 1} u_{j + 2} \dots u_{l} u_{r + 1} u_{r} \dots u_{l + 1} u_{s} u_{s + 1} \dots u_{j}$ 的示意图

Figure 13. Schematic diagram of path $u_{i + 1} u_{i} \dots u_{1} u_{j + 1} u_{j} \dots u_{l + 1} u_{s} u_{s + 1} \dots u_{l} u_{r + 1} u_{r} \dots u_{j + 2}$

图13. 存在路 $u_{i + 1} u_{i} \dots u_{1} u_{j + 1} u_{j} \dots u_{l + 1} u_{s} u_{s + 1} \dots u_{l} u_{r + 1} u_{r} \dots u_{j + 2}$ 的示意图

从而有， $d_{P_{2}} (u_{s}) + d_{P_{2}} (u_{r + 1}) \leq | X_{4} \cup Y_{4} | + | X_{4} \cap Y_{4} | \leq | V (P_{2}) | - 1 + | I_{4} |$ 。

因为 $u_{1} u_{2}, u_{r} u_{r + 1} \notin E (F)$ ，又 $u_{s}$ 是F上的孤立点，即 $u_{i + 1} u_{s}, u_{s} u_{i + 3} \notin E (F)$ ，故而 $I_{3} + I_{4} = E (F)$ 。因此， $d_{P} (u_{s}) + d_{P} (u_{r + 1}) \leq | V (P) | - 1 + | E (F) | = r + k$ 。

故而有， $d_{G} (u_{1}) + d_{G} (u_{s}) \leq n + k - 1$ ， $d_{G} (u_{s}) + d_{G} (u_{r + 1}) \leq n + k - 1$ ，又因为 $u_{1} u_{s} \notin E (G)$ ， $u_{s} u_{r + 1} \notin E (G)$ ，有 $d_{G} (u_{1}) + d_{G} (u_{s}) \geq n + k - 1$ ， $d_{G} (u_{s}) + d_{G} (u_{r + 1}) \geq n + k - 1$ ，所以 $d_{G} (u_{1}) + d_{G} (u_{s}) = n + k - 1$ ， $d_{G} (u_{s}) + d_{G} (u_{r + 1}) = n + k - 1$ 。

那么 $2 (d_{G} (u_{1}) + d_{G} (u_{s}) + d_{G} (u_{r + 1})) = 3 (n + k - 1)$ 。由 $ε (n, k) = 1$ 知，n，k奇偶性相同，而上式等号两边奇偶性不同，矛盾。所以假设不成立，定理8成立。

定理9 设G是阶 $n \geq k + t$ 的图，其中k，t为满足 $k \leq t$ 的正整数。设F是G中 $(k, t, t - k)$ -线性森林。如果

(i) $σ_{2} (G) \geq n + k$ ， $k = 1$ 时，

(ii) $σ_{2} (G) \geq n + k - ε (n, k)$ ， $k \geq 2$ 时，

则对任意 $r \in [\max {4, k + 2 t}, n]$ ，G中存在长为r或 $r + 1$ 的圈过F。

证明由引理6和引理7可知，G中存在长度不超过 $\max {4, k + 2 t}$ 的圈过F，记为 $C_{r_{0}}$ 。要证明定理9，只需证明在 $r \geq r_{0}$ 时，G中存在长度为r或 $r + 1$ 的圈过F。

用归纳法，当 $r = r_{0}$ 时，G中有长为r的圈过F，显然成立。

假设结论对给定的r成立，下面证对 $r + 1$ 也成立，即证G中有长度为 $r + 1$ 或 $r + 2$ 的圈过F。因为对于给定的r，有长为r或 $r + 1$ 的圈过F。如果存在长为 $r + 1$ 的圈过F，那么得证，如果不存在长为 $r + 1$ 的圈过F，那么存在长为r的圈过F，再由定理8可知，一定存在长为 $r + 2$ 的圈过F。故定理得证。

定理3的证明当 $F \neq P_{k + 1} \cup (t - 1) K_{1}$ 时，设G是含F的n阶图， $σ_{2} (G) \geq n + k - ε (n, k)$ 。在G中去掉F路中的所有内部点，即对于每条长度大于1的路，都用一条边将其代替，得到图 $G^{'}$ 。设总共去掉了 $k - k^{'}$ 个内部点，使得原线性森林F变成了 $(k^{'}, t)$ -线性森林 $F^{'}$ ，且新得到的线性森林每条路的长都为0或1，也即 $(k^{'}, t, t - k^{'})$ -线性森林。那么 $G^{'}$ 的阶数变为 $n^{'} = n - (k - k^{'}) = n - k + k^{'}$ 。对于 $G^{'}$ 中的任意两个不相邻点，其度和至多减少 $2 (k - k^{'})$ ，又有 $ε (n^{'}, k^{'}) = ε (n, k)$ ，所以 $σ_{2} (G^{'}) \geq n + k - ε (n, k) - 2 (k - k^{'}) = n^{'} + k^{'} - ε (n^{'}, k^{'})$ 。由定理9知，对任意 $r^{'} \geq \max {4, k^{'} + 2 t}$ 且 $r^{'} \leq n^{'}$ ，G中有长为 $r^{'}$ 或 $r^{'} + 1$ 的圈过 $F^{'}$ 。通过将 $G^{'}$ 中 $F^{'}$ 的每条边换成G中对应的路，就可由 $G^{'}$ 中过 $F^{'}$ 的圈得到相应的G中过F的圈，圈的长度对应变化，故而，对任意 $r \in [\max {4, k + 2 t}, n]$ ，G中存在长为r或 $r + 1$ 的圈过F。

当 $F = P_{k + 1} \cup (t - 1) K_{1}$ 时， $σ_{2} (G) \geq n + k$ ，通过类似的方法去内部点再还原，可得结论仍成立。故得证。

定理4的证明先证情况(i)， $F = P_{k + 1} \cup (t - 1) K_{1}$ 时。如果G是完全图，那么对于任意的 $(k, t)$ -线性森林，G中一定有一个哈密顿圈过这个线性森林。故而假设G不是完全图。设u、v是G中一对不相邻点， $V (H) = V (G) - {u, v}$ ，H是由 $V (H)$ 导出的G的子图。由前边定义有 $E (G) = d_{G} (u) + d_{G} (v) + E (H)$ 。又因为 $E (H) \leq (n - 2) (n - 3) / 2$ ，所以可以得到 $d_{G} (u) + d_{G} (v) = E (G) - E (H) \geq (n - 1) (n - 2) / 2 + k + 2 - (n - 2) (n - 3) / 2 = n + k$ ，因此由定理1可得，G是 $(k, t)$ -哈密顿的。

情况(ii)类似，同样通过定理1可证，故定理得证。

下面给出一个例子说明定理2情况(i)的界是紧的。令 $K_{n - 1}$ 是一个完全图，点集 $V (K_{n - 1}) = {v_{1}, v_{2}, \dots, v_{n - 1}}$ 外另有一点v，且v与 $K_{n - 1}$ 上的 $k + 1$ 个点 $v_{1}, v_{2}, \dots, v_{k + 1}$ 相邻，由这n个点构成的图即为图 $G_{1}$ 。可知 $E (G_{1}) = (n - 1) (n - 2) / 2 + k + 1$ 。取线性森林 $F_{1} = P_{k + 1} \cup (t - 1) K_{1}$ ，其中 $P_{k + 1} = v_{1} v_{2} \dots v_{k + 1}$ ，同时在 $K_{n - 1}$ 中另取 $t - 1$ 个其余点。显然， $G_{1}$ 中没有一个哈密顿圈能包含这个线性森林 $F_{1}$ 。

4. 结语

本文研究了在(i) $σ_{2} (G) \geq n + k$ ，当 $F = P_{k + 1} \cup (t - 1) K_{1}$ ，(ii) $σ_{2} (G) \geq n + k - ε (n, k)$ ，其他情况，这两种条件下，对任意 $r \in [\max {4, k + 2 t}, n]$ ，G中存在长为r或 $r + 1$ 的圈过 $(k, t)$ -线性森林的问题，是对Faudree提出的过 $(k, t)$ -线性森林的 $(k, t, 2 t + k)$ -泛圈问题新的探索，目前猜想并未被完全证明，仍是比较困难的问题。另一方面，本文从边数的角度给出了图G是 $(k, t)$ -哈密顿的一个条件。

文章引用

邵雅欣,杨卫华. 度和与边数条件下过线性森林圈的一些研究
Researches on the Cycles through Linear Forest under the Conditions of Degree Sum and Edge Number[J]. 应用数学进展, 2023, 12(01): 29-36. https://doi.org/10.12677/AAM.2023.121005

参考文献

1. Bondy, J.A. and Murty, U.S.R. (1976) Graph Theory with Applications. The Macmillan Press Ltd., Great Brit-ain.

2. Dirac, G.A. (1952) Some Theorems on Abstract Graphs. Proceedings of the London Mathematical Society, 3-2, 69-81. https://doi.org/10.1112/plms/s3-2.1.69

3. Ore O. (1960) Note on Hamilton Circuits. The American Mathematical Monthly, 67, 55. https://doi.org/10.2307/2308928

4. Kronk, H.V. (1969) A Note on K-Path Hamiltonian Graphs. Journal of Combinatorial Theory, 7, 104-106. https://doi.org/10.1016/S0021-9800(69)80043-8

5. Faudree, R.J., Gould, R.J. and Jacobson, M.S. (2009) Pan-cyclic Graphs and Linear Forests. Discrete Mathematics, 309, 1178-1189. https://doi.org/10.1016/j.disc.2007.12.094

6. 何剑. 度条件与过线性森林的圈[D]: [硕士学位论文]. 武汉: 华中师范大学, 2009.

NOTES

^*通讯作者。

期刊菜单