International Journal of Mechanics Research
Vol.06 No.02(2017), Article ID:21040,13
pages
10.12677/IJM.2017.62012
Critical Loads of Variable Cross-Section Compressive Rods Based on Precise Integration Method and Transfer Matrix Method
Die Wang, Fuliang Mei, Xiaoyi Chen, Liqing Xu, Hengqian Hu
College of Architecture & Civil Engineering,

Received: May 29th, 2017; accepted: Jun. 17th, 2017; published: Jun. 20th, 2017

ABSTRACT
A combination method of critical load of variable cross-section compressive rods was put forward based on precise integration method and transfer matrix method. First of all, the rod was divided into many sections and every section was viewed as uniform cross-section; the transfer matrixes of all the compressive sections were deduced according to theory of material mechanics, equilibrium principle and theory of matrix. Then the transfer matrix of whole variable cross-section compressive rod was obtained by means of deformation and internal force relationships between adjacent sections. Finally, a characteristic equation to solve the critical load of the variable cross-section compressive rod was presented. Results show that the present method is an easy one to program, control precisely and use conveniently.
Keywords:Variable Cross-Section, Compressive Rod, Precise Integration Method, Transfer Matrix Method, Critical Load
基于精细积分法和传递矩阵法 的变截面压杆临界力
王蝶,梅甫良,陈潇逸,徐丽青,胡恒谦
嘉兴学院建筑工程学院,浙江 嘉兴
收稿日期:2017年5月29日;录用日期:2017年6月17日;发布日期:2017年6月20日

摘 要
针对变截面压杆临界力提出了一种基于精细积分法和传递矩阵法的组合法。先将压杆离散为若干段,视每段压杆为等截面,采用材料力学理论、平衡原理及矩阵理论,导出了各段压杆的传递矩阵。然后利用相邻段间变形与内力关系,导出了整个变截面压杆的传递矩阵。最后,利用整个压杆两端约束条件,得到了求解变截面压杆临界力的特征方程。结果表明:本方法是一种易于编程、精度易于控制,也易于使用的方法。
关键词 :变截面,压杆,精细积分法,传递矩阵法,临界力

Copyright © 2017 by authors and Hans Publishers Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/


1. 引言
变截面压杆在工程中有着极其广泛的应用,如桥梁结构中的桥墩,特别是穿越山区桥梁结构的高桥墩,它的稳定性问题是工程设计人员必须考虑的关键问题之一。然而由于变截面压杆稳定性问题的计算理论十分复杂,因此,开展变截面压杆临界力简便计算方法的研究,具有极为重要的理论意义和工程意义。
近年来,国内外求解变截面压杆临界力的计算方法主要有:WBK法、传递矩阵法、能量法和有限单元法。马宝平等用改进的WBK法导出了变截面压杆的临界载荷方程,并计算了若干变截面(边长沿纵向坐标线性变化和型变截面)压杆的临界力 [1] 。刘庆潭等从压杆的微分方程出发,推导出了型和锥型压杆的传递矩阵,并给出了等厚度变高度和变截面圆压杆的临界力的数值解 [2] 。郑建军等在等截面压杆的传递矩阵基础上采用分段等截面近似假定和段间界面变形协调条件与力平衡条件导出了变截面压杆的累积传递矩阵,最后结合两端约束条件获得了其临界荷载特征方程 [3] 。之后,张煜也采用传递矩阵方法,给出了含中间弹性支承的阶梯型压杆临界力的计算公式 [4] 。谢海等采用最小势能原理和满足两端位移约束条件的系列试函数导出了求解变截面压杆临界压力的计算公式 [5] 。卞敬玲等采用有限单元法推导出计算任意变截面压杆稳定问题的有限元列式 [6] 。
本文提出了基于精细积分法和传递矩阵法的变截面压杆临界力的组合法,供工程设计人员使用。
2. 变截面压杆的传递矩阵
2.1. 等截面压杆的传递矩阵
考虑长度为 、轴线为直线、无初始弯曲和质量均匀分布的变截面压杆。将沿压杆轴向离散为N段,记第i段压杆的长度和惯性矩分别为
、轴线为直线、无初始弯曲和质量均匀分布的变截面压杆。将沿压杆轴向离散为N段,记第i段压杆的长度和惯性矩分别为 和
和
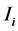 ,其中
,其中 根据第i段压杆中间截面尺寸来计算。当段数N足够大时,这样的处理结果能够达到精度要求。由第i段压杆中长度为
根据第i段压杆中间截面尺寸来计算。当段数N足够大时,这样的处理结果能够达到精度要求。由第i段压杆中长度为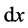 的微段内力平衡和材料力学理论,可得:
的微段内力平衡和材料力学理论,可得:
 (1)
(1)
式中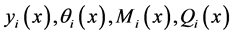 分别为距第i段压杆上端为
分别为距第i段压杆上端为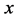 处的挠度,转角,弯矩和剪力。上式(1)可改写为如下矩阵形式:
处的挠度,转角,弯矩和剪力。上式(1)可改写为如下矩阵形式:
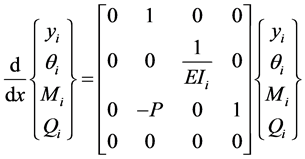 (2)
(2)
引入符号:
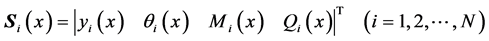 (3)
(3)
式中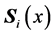 称为距离第i段压杆上端为
称为距离第i段压杆上端为 处的状态向量,和
处的状态向量,和
 (4)
(4)
式(2)可改写为如下状态方程:
 (5)
(5)
利用矩阵分析理论,式(5)的解为:
 (6)
(6)
式中 为第i段压杆上端的状态向量,其中
为第i段压杆上端的状态向量,其中 为第i段压杆上端的挠度,转角,弯矩和剪力。当
为第i段压杆上端的挠度,转角,弯矩和剪力。当 时,由式(6),可得第i段压杆上、下端状态向量之间的关系式:
时,由式(6),可得第i段压杆上、下端状态向量之间的关系式:
 (7)
(7)
式中 为第i段压杆下端的状态向量,其中
为第i段压杆下端的状态向量,其中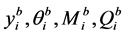 为第i段下端的挠度,转角,弯矩和剪力。
为第i段下端的挠度,转角,弯矩和剪力。
引入 符号:
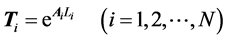 (8)
(8)
式中 为第i段压杆的传递矩阵,它的求解采用如下的精细积分方法进行,将式(8)表示为:
为第i段压杆的传递矩阵,它的求解采用如下的精细积分方法进行,将式(8)表示为:
 (9)
(9)
其中 ,例如
,例如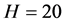 ,则
,则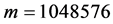 。令
。令 。
。
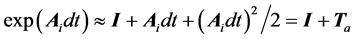 (10)
(10)
其中
 (11)
(11)
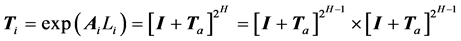 (12)
(12)
注意到
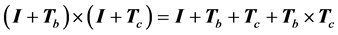 (13)
(13)
因此式(12)相当于执行语句:
 (14)
(14)
当循环结束时有:
 (15)
(15)
2.2. 整个变截面压杆的传递矩阵
从第1段到最后第N段连续使用方程(7)和(15),可得整个变截面压杆上、下端状态向量之间的关系式:
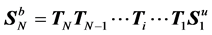 (16)
(16)
式中 为第1段压杆上端的状态向量,其中
为第1段压杆上端的状态向量,其中 为第1段上端的挠度,转角,弯矩和剪力;
为第1段上端的挠度,转角,弯矩和剪力; 为第N段压杆下端的状态向量,其中
为第N段压杆下端的状态向量,其中 为第N段压杆下端的挠度,转角,弯矩和剪力。
为第N段压杆下端的挠度,转角,弯矩和剪力。
引入符号:
 (17)
(17)
式中 称为整个变截面压杆的传递矩阵。
称为整个变截面压杆的传递矩阵。
3. 求解变截面压杆临界力的特征方程
利用变截面压杆上、下端约束条件和方程式(17),可得求解变截面压杆临界力的特征方程。以下给出常见的五种不同约束条件的特征方程。
(1) 当上、下端均为铰支时,即 ,其特征方程为
,其特征方程为
 (18)
(18)
(2) 当上、下端均为固支时,即 ,其特征方程为
,其特征方程为
 (19)
(19)
(3) 当上端自由、下端固支时,即 ,其特征方程为
,其特征方程为
 (20)
(20)
(4) 当上端铰支、下端固支时,即 ,其特征方程为
,其特征方程为
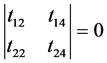 (21)
(21)
(5) 当上端可侧移而不转动、下端固支时,即 ,其特征方程为:
,其特征方程为:
 (22)
(22)
4. 求解变截面压杆临界力的迭代过程
在数学上,变截面压杆临界力的解析求解十分困难,只能采用数值方法求解。本文采用迭代法,其迭代过程如下:
第一步:先视整个变截面压杆为等截面且其截面等同于最小截面,根据最小截面处的抗弯刚度 与两端约束条件,按材料力学细长压杆临界力公式,计算出试算临界力的初始值
与两端约束条件,按材料力学细长压杆临界力公式,计算出试算临界力的初始值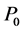 和等量增量值
和等量增量值 ,其中
,其中 。
。
第二步:试算临界力 (其中j代表试算次数),将
(其中j代表试算次数),将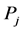 代入式(4),计算
代入式(4),计算 ,
,
 和
和 ,根据压杆两端约束条件所对应的临界力的特征方程计算其行列式值
,根据压杆两端约束条件所对应的临界力的特征方程计算其行列式值 ;增加循环次数
;增加循环次数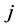 ,重复第二步上述过程,直到
,重复第二步上述过程,直到 符号发生改变为止。此时,记当前行列式值为
符号发生改变为止。此时,记当前行列式值为 ,所对应的临界力上限为
,所对应的临界力上限为 ,前一次试算行列式值记为
,前一次试算行列式值记为 ,所对应的临界力下限为
,所对应的临界力下限为 。
。
第三步:采用二分法搜索如下:(1) 记 ,将
,将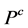 代入式(4),计算
代入式(4),计算 ,
,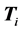 ,
, ,
,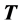 ,所对应的行列式值
,所对应的行列式值 ;(2) 如果
;(2) 如果 ,则
,则 ,
, ,
, 和
和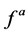 不变;如果
不变;如果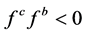 ,则
,则 ,
, ,
, 和
和 不变。重复第三步中(1)和(2),直到满足下列式(23)的收敛性条件为止。
不变。重复第三步中(1)和(2),直到满足下列式(23)的收敛性条件为止。
 (23)
(23)
式中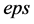 为二分法迭代搜索法的收敛控制允许值。
为二分法迭代搜索法的收敛控制允许值。
5. 算例与分析
基于上述计算公式,编制了计算程序,见附件1。算例一:考虑长度为10 m的锥型变截面压杆,其横截面为正方形,上端面边长为 ,下端面边长为
,下端面边长为 。压杆材料的弹性模量
。压杆材料的弹性模量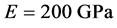 。上、下端约束条件有五种情况。将此杆均匀离散为N段,经过多次试算后可知当N取得足够大,比如第一种约束条件①且下端边长
。上、下端约束条件有五种情况。将此杆均匀离散为N段,经过多次试算后可知当N取得足够大,比如第一种约束条件①且下端边长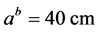 ,N大于50之后,所得的临界力趋于稳定值;当然,随着上、下端边长(
,N大于50之后,所得的临界力趋于稳定值;当然,随着上、下端边长( )的增加,N应取大一些,总之,本方法的收敛速度很快,且计算精度也很高。基于本文解和Ansys大型结构有限元分析系统,对上述锥型变截面压杆在五种常见不同约束条件下临界力进行了计算,各种约束条件下临界力
)的增加,N应取大一些,总之,本方法的收敛速度很快,且计算精度也很高。基于本文解和Ansys大型结构有限元分析系统,对上述锥型变截面压杆在五种常见不同约束条件下临界力进行了计算,各种约束条件下临界力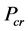 的本文精细积分法结果与Ansys有限元结果,列于表1中。应用Ansys有
的本文精细积分法结果与Ansys有限元结果,列于表1中。应用Ansys有
Tabel 1. Critical load Pcr of taper-varied cross-section compressive rods under five different constraints (unit: MN)
表1. 五种常见约束条件下锥型变截面压杆的临界力Pcr (单位:MN)
 (a) 上、下端均为铰支
(a) 上、下端均为铰支  (b) 上、下端均为固支
(b) 上、下端均为固支 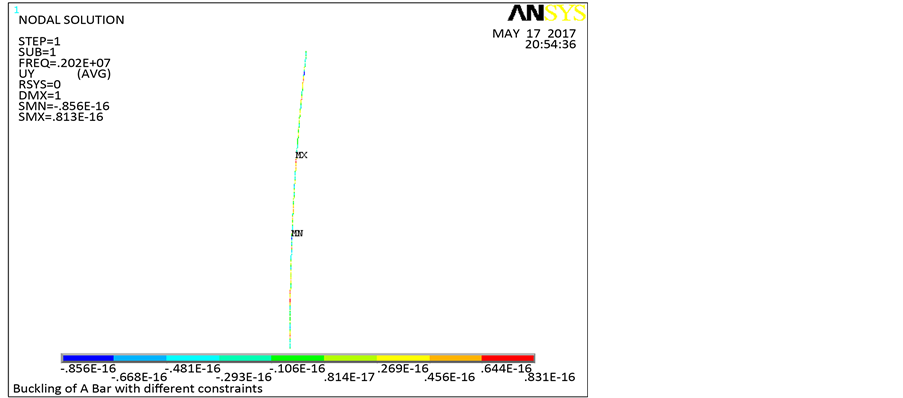 (c) 上端自由、下端固支
(c) 上端自由、下端固支  (d) 上端铰支、下端固支
(d) 上端铰支、下端固支 (e) 上端可侧移不转动、下端固支
(e) 上端可侧移不转动、下端固支
Figure 1. The first order buckling mode of taper-varied cross-section compressive rods under five different constraints with Ansys software
图1. 用Ansys软件所得的五种不同约束条件下锥型变截面压杆的第一阶屈曲模态
Tabel 2. Critical load Pcr of three ladder cross-section compressive rods under five different constraints (unit: MN)
表2. 五种常见约束条件下三阶梯型截面压杆的临界力Pcr (单位:MN)
 (a) 上、下端均为铰支
(a) 上、下端均为铰支  (b) 上、下端均为固支
(b) 上、下端均为固支 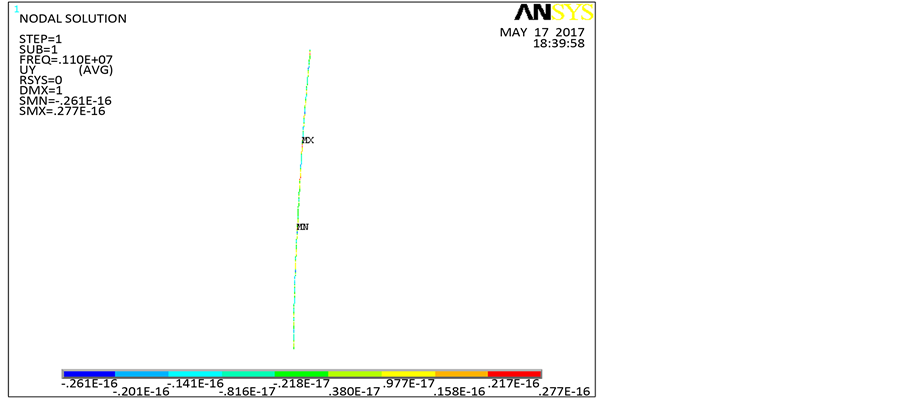 (c) 上端自由、下端固支
(c) 上端自由、下端固支  (d) 上端铰支、下端固支
(d) 上端铰支、下端固支 (e) 上端可侧移不转动、下端固支
(e) 上端可侧移不转动、下端固支
Figure 2. The first order buckling mode of three-ladder cross-section compressive rods Under five different constraints with Ansys software
图2. 用Ansys软件所得的五种不同约束条件下三阶梯型截面压杆的第一阶屈曲模态
限元法计算所得的五种常见约束条件下锥型变截面压杆的第一阶屈曲模态如图1所示。使用Ansys时,采用的单元是平面梁单元(Beam3),将整个压杆均匀离散为100个梁单元,每单元实常数(截面面积、轴惯性矩和高度)都采用该单元中间截面尺寸来计算。
算例二:考虑三阶梯型圆截面压杆,上段压杆长度和直径分别为3 m和20 cm,中段压杆长度和直径分别为4 m和30 cm,下段压杆长度和直径分别为3 m和25 cm。上、下端约束条件与算例一相同,它们各自初始临界力试算值 ,其中
,其中 。与算例一不同的是:不需要人为离散,只要自然方式分为三段进行计算。计算结果如表2所示。用Ansys有限元法所得的五种常见约束下三阶梯型截面压杆的第一阶屈曲模态如图2所示。
。与算例一不同的是:不需要人为离散,只要自然方式分为三段进行计算。计算结果如表2所示。用Ansys有限元法所得的五种常见约束下三阶梯型截面压杆的第一阶屈曲模态如图2所示。
从表1和表2可见,各种约束下变截面压杆临界力的本文数值结果与Ansys结果十分接近,两者之间相对误差最大只有3.5%。因此,本文提出的精细积分法是一种计算精度很高的计算方法,而且只要编制一小段程序,输入几个参数,使用起来十分方便。
6. 结论
本文对变截面压杆临界力求解方法提出了一种基于精细积分法和传递矩阵法的组合法,并导出了相关计算公式,以及提供了传递矩阵的精细积分法求解过程和求解临界力搜索二分法的求解过程,编制了计算程序。算例结果验证了本文方法是一种易于编程、精度易于控制、实用较为方便的方法,值得推广。
基金项目
嘉兴学院2016年度校级一般SRT计划项目(No. SRT2016C162)。
文章引用
王 蝶,梅甫良,陈潇逸,徐丽青,胡恒谦. 基于精细积分法和传递矩阵法的变截面压杆临界力
Critical Loads of Variable Cross-Section Compressive Rods Based on Precise Integration Method and Transfer Matrix Method[J]. 力学研究, 2017, 06(02): 101-113. http://dx.doi.org/10.12677/IJM.2017.62012
参考文献 (References)
- 1. 马宝平, 郭树起, 冯自进. 变截面压杆的临界荷载计算[J]. 石家庄铁道大学学报(自然科学版), 2003, 26(2): 106- 110.
- 2. 刘庆潭, 倪国荣. 变截面压杆稳定计算的传递矩阵法[J]. 长沙铁道学院学报, 1995, 13(3): 60-66.
- 3. 郑建军, 刘兴业. 任意变截面压杆稳定计算的传递矩阵法[J]. 天津城建学院学报, 1994(1-2): 52-54.
- 4. 张煜. 变截面压杆稳定性分析的矩阵传递法[J]. 贵州工业大学学报(自然科学版), 2000, 29(5): 7-12.
- 5. 谢海, 寿开荣, 李龙, 李剑敏. 基于最小势能原理的变截面压杆临界压力的计算方法[J]. 浙江理工大学学报, 2013, 30(1): 87-89.
- 6. 卞敬玲, 王小岗. 变截面压杆稳定计算的有限单元法[J]. 武汉大学学报(工学版), 2002, 35(4): 102-104.
附件1:求解锥型变截面压杆临界力的计算程序
clear all
E = 2e11; %压杆材料的弹性模量,单位:N/m2
L = 10; %整个压杆的轴向长度,单位:m
au = 0.20; %压杆上端正方形截面的边长,单位:m
ab = 0.40; %压杆下端正方形截面的边长,单位:m
N = 100; %压杆分段总数
Li = L/N; %压杆每段长度,单位:m
Type = 3; %压杆两端约束类型编号,1:两端铰支;2:两端固支;3:上端自由、%下端固支;4:上端铰支、下端固支;5:上端可侧向移动二而不转动、%下端固支。
I1 = au^4/12;
Eps = 1e3;
eps1 = 0.01;
if Type = 1
P0 = pi^2*E*I1/L^2;
DP = P0/Eps;
elseif Type = 2
P0 = pi^2*E*I1/(0.5*L)^2;
DP = P0/Eps;
elseif Type = 3
P0 = pi^2*E*I1/(2*L)^2;
DP = P0/Eps;
elseif Type = 4
P0 = pi^2*E*I1/(0.7*L)^2;
DP = P0/Eps;
elseif Type = 5
P0 = pi^2*E*I1/L^2;
DP = P0/Eps;
end
f = 1;
ii = 1;
while f > 0 %先通过逐步递推,找出解的大致范围
ii = ii+1;
Pi = P0+ii*DP;
a1 = au+(ab-au)*Li*(1-1/2)/L;
I1 = a1^4/12;
A1 = [0 1 0 0;0 0 1/(E*I1) 0;0 -Pi 0 1;0 0 0 0];
T1 = expm(A1*Li);
for j = 2:N
ai = au+(ab-au)*Li*(j-1+1/2)/L;
Ii = ai^4/12;
Ai = [0 1 0 0;0 0 1/(E*Ii) 0;0 -Pi 0 1;0 0 0 0];
Ti = expm(Ai*Li);
T = Ti*T1;
T1 = T;
end
if Type = 1
f = T(1,2)*T(3,4)-T(1,4)*T(3,2);
elseif Type = 2
f = T(1,3)*T(2,4)-T(1,4)*T(2,3);
elseif Type = 3
f = T(1,1)*T(2,2)-T(1,2)*T(2,1);
elseif Type = 4
f = T(1,2)*T(2,4)-T(1,4)*T(2,2);
elseif Type = 5
f = T(1,1)*T(2,3)-T(1,3)*T(2,1);
end
end
%以下精确找出变截面压杆临界力的解
Pu = Pi-DP; %临界力的下界
Pb = Pi; %临界力的上界
Pc = (Pu+Pb)/2; %临界力的平均值
fu = 1;
fb = f;
a1 = au+(ab-au)*Li*(1-1/2)/L;
I1 = a1^4/12;
A1 = [0 1 0 0;0 0 1/(E*I1) 0;0 -Pc 0 1;0 0 0 0];
T1 = expm(A1*Li);
for j = 2:N
ai = au+(ab-au)*Li*(j-1+1/2)/L;
Ii = ai^4/12;
Ai = [0 1 0 0;0 0 1/(E*Ii) 0;0 -Pc 0 1;0 0 0 0];
Ti = expm(Ai*Li);
T = Ti*T1;
T1 = T;
end
if Type = 1
fc = T(1,2)*T(3,4)-T(1,4)*T(3,2);
elseif Type = 2
fc = T(1,3)*T(2,4)-T(1,4)*T(2,3);
elseif Type = 3
fc = T(1,1)*T(2,2)-T(1,2)*T(2,1);
elseif Type = 4
fc = T(1,2)*T(2,4)-T(1,4)*T(2,2);
elseif Type = 5
fc = T(1,1)*T(2,3)-T(1,3)*T(2,1);
end
while (Pb-Pu)/Pc > eps1
if fc*fb > 0
Pb = Pc;
fb = fc;
Pu = Pu;
fu = fu;
Pc = (Pb+Pu)/2;
else
Pu = Pc;
fu = fc;
Pb = Pb;
fb = fb;
Pc = (Pb+Pu)/2;
end
a1 = au+(ab-au)*Li*(1-1/2)/L;
I1 = a1^4/12;
A1 = [0 1 0 0;0 0 1/(E*I1) 0;0 -Pc 0 1;0 0 0 0];
T1 = expm(A1*Li);
for j = 2:N
ai = au+(ab-au)*Li*(j-1+1/2)/L;
Ii = ai^4/12;
Ai = [0 1 0 0;0 0 1/(E*Ii) 0;0 -Pc 0 1;0 0 0 0];
Ti = expm(Ai*Li);
T = Ti*T1;
T1 = T;
end
if Type = 1
fc = T(1,2)*T(3,4)-T(1,4)*T(3,2);
elseif Type = 2
fc = T(1,3)*T(2,4)-T(1,4)*T(2,3);
elseif Type = 3
fc = T(1,1)*T(2,2)-T(1,2)*T(2,1);
elseif Type = 4
fc = T(1,2)*T(2,4)-T(1,4)*T(2,2);
elseif Type = 5
fc = T(1,1)*T(2,3)-T(1,3)*T(2,1);
end
end
Pc