Pure Mathematics
Vol.4 No.05(2014), Article
ID:14076,3
pages
DOI:10.12677/PM.2014.45028
The Centre of Quantum Weyl Algebras
School of Mathematics, Shanghai University of Finance and Economics, Shanghai
Email: liuluningde@163.com, yhw@mail.shufe.edu.cn
Copyright © 2014 by authors and Hans Publishers Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/



Received: Jul. 16th, 2014; revised: Aug. 15th, 2014; accepted: Aug. 24th, 2014
ABSTRACT
This paper shows that the centre of (−1)-quantum Weyl algebra 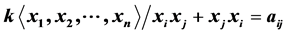 is generated by
is generated by .
.
Keywords:Weyl Algebra, Quantum Weyl Algebra, Centre of an Algebra, Cohomology

量子Weyl代数的中心
柳鲁宁,王艳华
上海财经大学数学学院,上海
Email: liuluningde@163.com, yhw@mail.shufe.edu.cn
收稿日期:2014年7月16日;修回日期:2014年8月15日;录用日期:2014年8月24日

摘 要
本文给出了(−1)-量子Weyl代数 的中心是由
的中心是由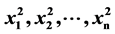 生成的。
生成的。
关键词
Weyl代数,量子Weyl代数,代数的中心,上同调

1. 引言
设 是一个代数,
是一个代数, 的中心定义为代数中与所有元素可交换的元素集合,即
的中心定义为代数中与所有元素可交换的元素集合,即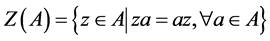 。代数的中心对刻画代数本身的性质具有重要作用,如一个代数的零次上同调群就是代数的中心,即
。代数的中心对刻画代数本身的性质具有重要作用,如一个代数的零次上同调群就是代数的中心,即 。另外,在新近的研究中,我们发现代数的中心对于研究代数的自同构群也起着重要作用,见参考文献[1] [2] 。以往的代数学者大多关注代数中心的性质,见参考文献[3] -[5] ,所研究代数涉及群代数、Leavitt路代数、Effect代数、Kumjian-Pask代数等众多代数,见参考文献[6] -[9] ,但对于计算代数的中心鲜少研究。
。另外,在新近的研究中,我们发现代数的中心对于研究代数的自同构群也起着重要作用,见参考文献[1] [2] 。以往的代数学者大多关注代数中心的性质,见参考文献[3] -[5] ,所研究代数涉及群代数、Leavitt路代数、Effect代数、Kumjian-Pask代数等众多代数,见参考文献[6] -[9] ,但对于计算代数的中心鲜少研究。
量子Weyl代数诞生于上世纪30年代。该代数具有独特的物理背景,是一个典型的结构清晰的无限维非交换代数,其涉及领域之广、研究成果之丰富在非交换代数领域中可以说是独一无二的。研究表明,量子Weyl代数与Lie代数、微分算子代数、代数几何、D2模理论、Artin-Schelter正则代数以及非交换代数几何都有着深刻的联系,为非交换代数理论的发展提供了许多行之有效和值得借鉴的方法。一些代数学者把(量子)Weyl代数作为非交换代数研究的一个范例,例如Weyl代数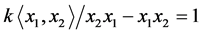 作为一类具体的2维Artin-Schelter正则代数,其在非交换代数的研究中占据重要的地位,它的许多性质揭示了2维Artin-Schelter正则代数的性质。
作为一类具体的2维Artin-Schelter正则代数,其在非交换代数的研究中占据重要的地位,它的许多性质揭示了2维Artin-Schelter正则代数的性质。
实际上,求一个具体的代数的中心不是一件简单的事情,有些代数的中心即使借助计算机辅助计算也很难找到。目前,一些代数的中心我们还不是很清楚,这在一定程度上阻碍了这些代数的进一步发展。本文以(−1)-量子Weyl代数为例,从代数的生成元和生成关系出发,给出了(−1)-量子Weyl代数的中心。此结果对于进一步研究量子Weyl代数的性质,特别是自同构群的刻画起着重要作用。
2. (−1)-量子Weyl代数的中心
设 是特征为0的域。令
是特征为0的域。令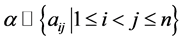 是
是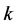 中的数集,(−1)-量子Weyl代数
中的数集,(−1)-量子Weyl代数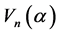 定义为由
定义为由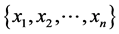 生成且满足关系:
生成且满足关系: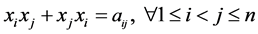 的代数,一般地我们表示为
的代数,一般地我们表示为 。利用diamond lemma,易知其基为
。利用diamond lemma,易知其基为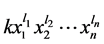 ,其中
,其中 。
。
本文主要讨论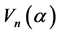 的中心。首先,我们观察到生成元
的中心。首先,我们观察到生成元 不可能是
不可能是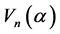 的中心元,否则,
的中心元,否则,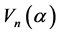 就是一个交换代数。我们有下面的引理:
就是一个交换代数。我们有下面的引理:
引理2.1设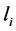 、
、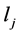 是正整数。如果
是正整数。如果 、
、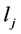 中有一个为偶数,则我们有
中有一个为偶数,则我们有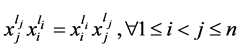 。
。
证明:由代数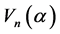 的生成关系
的生成关系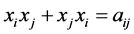 ,我们有
,我们有 ,则有:
,则有:
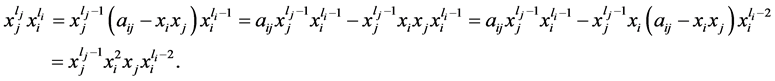 (1)
(1)
依次进行下去,(1)式等于
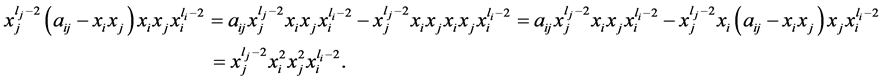 (2)
(2)
每次当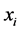 与前面的
与前面的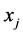 交换位置时用公式
交换位置时用公式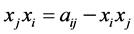 。这样,由(1)、(2)两式我们有:
。这样,由(1)、(2)两式我们有:
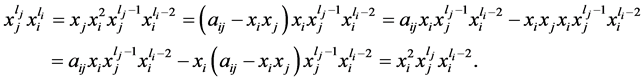 (3)
(3)
对(3)式继续上述过程,我们有如下的方程:
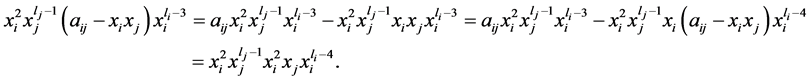 (4)
(4)
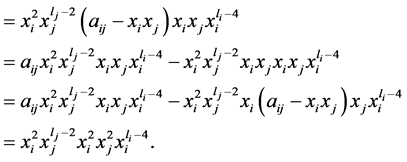 (5)
(5)
这样,重复上述过程,由(4)、(5)两式,我们可以得到:
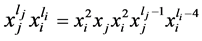
对上式右端再重复以上的过程,我们可以得到:
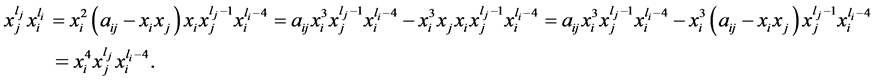 (6)
(6)
(3)、(6)两式意味着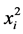 、
、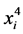 与
与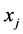 可以交换。如果
可以交换。如果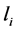 是偶数,继续以上过程,则有:
是偶数,继续以上过程,则有:
 (7)
(7)
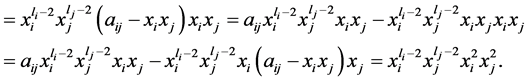 (8)
(8)
这样,由(7)、(8)两式,我们可以得到:
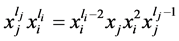
对上式右端再重复以上的过程,我们可以得到:
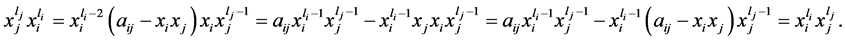
即当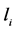 是偶数时,我们得到结论正确。类似地,当
是偶数时,我们得到结论正确。类似地,当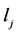 是偶数时,我们也可以证明如上结论正确。
是偶数时,我们也可以证明如上结论正确。
引理2.2设 、
、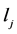 是正整数。若
是正整数。若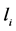 、
、 均为奇数,我们有
均为奇数,我们有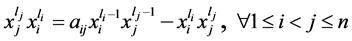 。
。
证明:如果 是奇数,则由(3)、(6)两式,我们有:
是奇数,则由(3)、(6)两式,我们有:
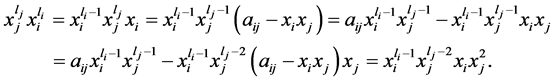 (9)
(9)
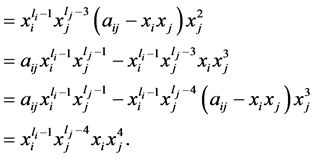 (10)
(10)
如果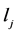 是奇数,则由(9)、(10)两式,我们有:
是奇数,则由(9)、(10)两式,我们有:
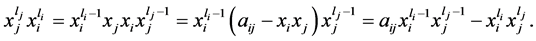
引理2.1和引理2.2表明,当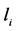 和
和 都是奇数时,每次交换都会出现
都是奇数时,每次交换都会出现 这样的项,所以此时
这样的项,所以此时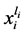 ,
,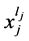 不能交换,这也就说明
不能交换,这也就说明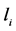 、
、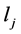 的奇数次幂不会是中心元。
的奇数次幂不会是中心元。
下面假设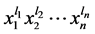 是代数
是代数 的中心元,鉴于以上两个引理,我们只需考虑
的中心元,鉴于以上两个引理,我们只需考虑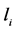 取0或1的情形,其中
取0或1的情形,其中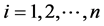 。
。
引理2.3设 只能取0或1,且
只能取0或1,且 不全为0,则
不全为0,则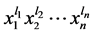 不是
不是 的中心元。
的中心元。
证明:反证法,如果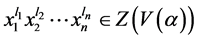 ,则对任意的
,则对任意的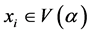 ,有:
,有:
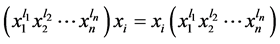 。
。
不妨设 ,
, ,则有:
,则有:

所以,
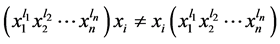
这样, 。
。
定理2.4我们有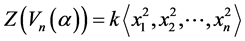 。
。
证明:由引理2.1知,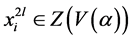 ,
,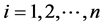 ,
,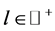 ,而由引理2.2知,
,而由引理2.2知, ,
,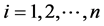 ,
,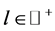 。进一步由引理2.3可知,
。进一步由引理2.3可知,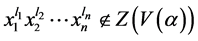 ,其中
,其中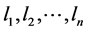 取0或1。所以,我们得到
取0或1。所以,我们得到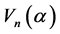 的中心就是由
的中心就是由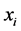 ,
,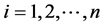 的偶次幂生成的。至此完成了定理的证明。
的偶次幂生成的。至此完成了定理的证明。
参考文献 (References)
- [1] Ceken, S., Palmieri, J., Wang, Y.H. and Zhang, J.J. (2013) The discriminant controls automorphism groups of noncom mutative algebras. arXiv:1401.0793.
- [2] Ceken, S., Palmieri, J.H., Wang, Y.H. and Zhang, J.J. (2014) The discriminant criterion and automorphism groups of quantized algebras. arXiv:1402.6625.
- [3] Davydov, A., Kong, L. and Runkel, I. (2013) Functoriality of the center of an algebra. arXiv:1307.5956.
- [4] Davydov, A. (2010) Centre of an algebra. Advances in Mathematics, 1, 319-348.
- [5] Davydov, A. (2012) Full centre of an H-module algebra. Communications in Algebra, 1, 273-290.
- [6] Rosenberg, A. (1961) Blocks and centres of group algebras. Mathematische Zeitschrift, 1, 209-216.
- [7] Pino, G.A. and Crow, K. (2011) The center of a Leavitt path algebra. Revista Matemática Iberoamericana, 2, 621-644.
- [8] Greechie, R.J., Foulis, D. and Pulmannová, S. (1995) The center of an effect algebra. Order, 1, 91-106.
- [9] Brown, J.H. (2012) The center of a Kumjian-Pask algebra. arXiv:1209.2627.