Pure Mathematics
Vol.05 No.02(2015), Article ID:14934,6
pages
10.12677/PM.2015.52009
Blowup of Solutions for a Class of Doubly Nonlinear Parabolic Equations
Jing Su, Longfei Qi, Qingying Hu
College of Science, Henan University of Technology, Zhengzhou Henan
Email: slxhqy@163.com
Received: Feb. 27th, 2015; accepted: Mar. 8th, 2015; published: Mar. 12th, 2015
Copyright © 2015 by authors and Hans Publishers Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/



ABSTRACT
This paper is concerned with a class of doubly nonlinear parabolic systems. Under the homogeneous Dirichlet conditions and suitable conditions on the nonlinearity and certain initial datum, a sufficient condition for finite time blowup of its solution in a bounded domain is gave by using a modification of Levine’s concavity method.
Keywords:Blowup of Solution, Doubly Nonlinear Parabolic Equations, Levine’s Concavity Method
多重非线性抛物方程组解的爆破
苏璟,齐龙飞,呼青英
河南工业大学理学院,河南 郑州
Email: slxhqy@163.com
收稿日期:2015年2月27日;录用日期:2015年3月8日;发布日期:2015年3月12日

摘 要
本文研究了一类多重非线性抛物方程组解的爆破,利用修正的Levine凸性方法,对齐次Dirichlet边界和非线性项和初始条件的适当条件下,给出了解爆破时间的充分条件。
关键词 :爆破,多重非线性抛物方程组,Levine凸性方法

1. 引言
本文研究如下非线性抛物方程组解的爆破性
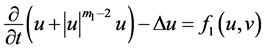 (1.1)
(1.1)
 (1.2)
(1.2)
 (1.3)
(1.3)
 (1.4)
(1.4)
其中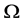 是
是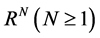 上的有界区域且有光滑边界
上的有界区域且有光滑边界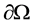 ,
,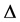 是
是 上的Laplace 算子,
上的Laplace 算子, ,
,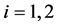 为以后给定的函数。
为以后给定的函数。
型如(1.1)的单个多重非线性抛物方程
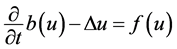 (1.5)
(1.5)
就是经典的所谓双非线性抛物方程,这类方程可以描述诸多化学反应、热传导过程和种群动力学过程(详细见文献[1] )。方程(1.5)的初值问题或初边值问题已经有许多文献研究其局部和整体可解性[2] -[6] ,文献[7] -[12] 则研究了其整体吸引子的存在性和正则性。最近几十年,该类非线性抛物方程的爆破问题吸引了许多人的注意,基于Levine [13] [14] 凸性方法这一开创性的证明爆破的结果,Iami和Mochizuki [15] 则给出了方程(1.5)带Neumann初边值问题解爆破的充分条件,该凸性方法还被Levine [16] [17] 用于如下渗流方程
 (1.6)
(1.6)
Sacks [18] 研究了如下包含方程解的爆破问题
 (1.7)
(1.7)
Zhang [19] 和Ding和Guo [20] -[22] 通过构造适当的辅助函数,利用一阶微分不等式考虑了下面带梯度项和Neumann (或Robin)初边值问题解的爆破条件
 (1.8)
(1.8)
Korpusou和Sveshnikov [23] [24] 给出了如下方程初边值问题弱解爆破的充分条件
 (1.9)
(1.9)
最后,还应提及Ouardi和 Hachimi [25] [26] 研究了如下多重非线性抛物方程组
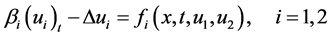
得到了其整体吸引子的存在性和正则性以及Hausdorff维数估计。
本文用修正的Levine凸性方法证明问题(1.1)~(1.4)的解在有限时刻爆破,该方法比原始的Levine凸性方法更简洁,其基本技巧是Korpousov [24] 给出的一个微分不等式,本文把[24] 的方法用于多重非线性抛物方程组。据作者所知,关于多重非线性抛物方程组的爆破问题的研究还比较少。本文的安排如下:第二节将给出一些假设和基本引理,第三节给出主要结果和证明。
2. 假设和基本引理
本文用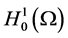 和
和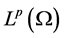 表示通常的Soblev空间,其范数分别记为
表示通常的Soblev空间,其范数分别记为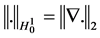 和
和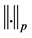 ,特别是当
,特别是当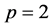 时,记
时,记 ,这些符号的含义和记法同文献[2] 。
,这些符号的含义和记法同文献[2] 。
本文始终假设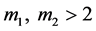 。关于非线性项
。关于非线性项 ,
, 的假设如下:
的假设如下:
(A1) ,存在函数
,存在函数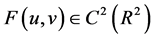 使得
使得
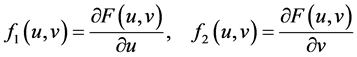 ,
,
且存在常数 使得
使得
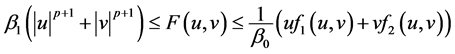 ,
,
其中,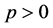 当
当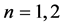 时,
时, 当
当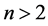 时。
时。
注:满足条件(A1)的函数是存在的。事实上,一个典型的例子是取
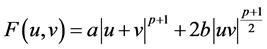
且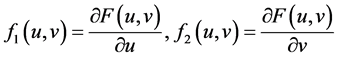 ,即
,即
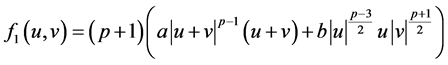 ,
,
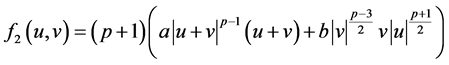 ,
,
这时,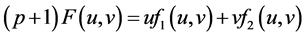 ,其中
,其中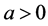 ,
, ,
, ,
,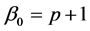 。该例的详细情况可见文献[27] 。
。该例的详细情况可见文献[27] 。
利用Galerkin方法,结合单调性理论和紧性方法[2] ,类似文献[24] 可得问题(1.1)~(1.4)解的局部存在性。
定理2.1:假设条件(A1)成立,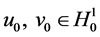 ,
,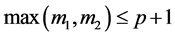 ,则问题(1.1)~(1.4)存在弱解
,则问题(1.1)~(1.4)存在弱解 ,即,存在
,即,存在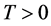 使得
使得
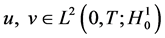 ,
, 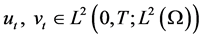 ,
,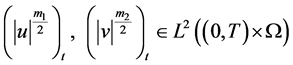 .
.
且对任意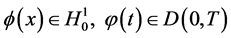 成立:
成立:
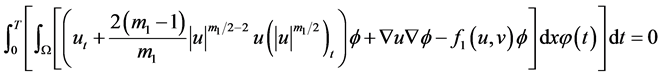 ,
,
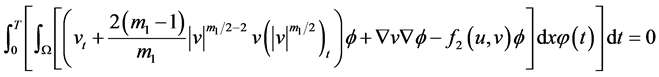 ,
,
以及 。
。
下面给出本文的基本引理。
引理2.2 [13] [24] [28] :设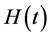 是R上非负二次连续可导函数且满足不等式
是R上非负二次连续可导函数且满足不等式
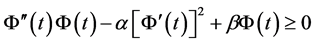
其中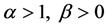 为常数。若
为常数。若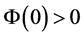 ,
,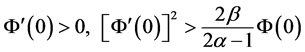 ,则必存在时刻
,则必存在时刻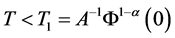 ,使当
,使当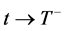 时有
时有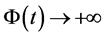 ,其中
,其中
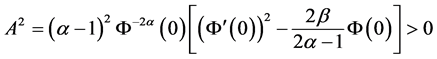 。
。
3. 主要结果及证明
首先引入泛函
 (3.1)
(3.1)
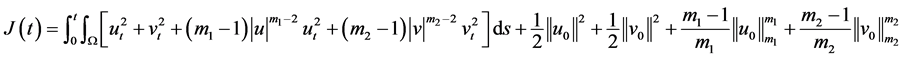 (3.2)
(3.2)
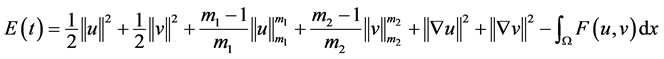 (3.3)
(3.3)
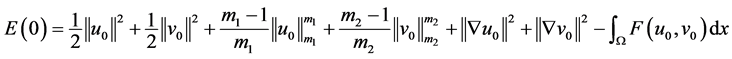 (3.4)
(3.4)
现给出主要引理。
引理3.1:对任意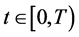 ,下面不等式成立
,下面不等式成立
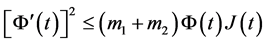 (3.5)
(3.5)
证明 注意到
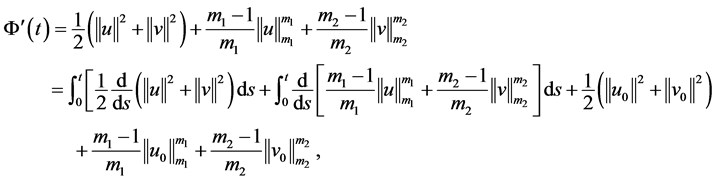 (3.6)
(3.6)
而由Holder不等式得
 (3.7)
(3.7)
 (3.8)
(3.8)
 (3.9)
(3.9)
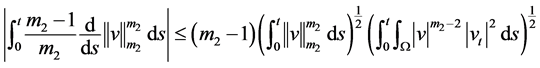 (3.10)
(3.10)
考虑到(3.7)~(3.10),则由(3.6)得

再利用不等式
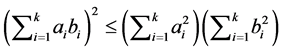 ,
,
得
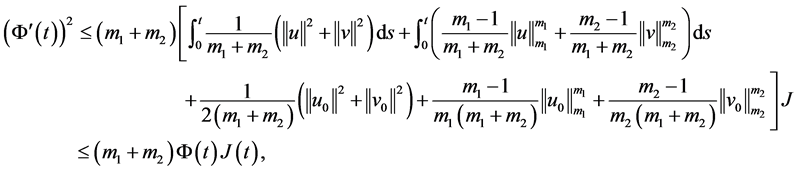
于是,引理得证。
下面,给出主要定理。
定理3.2:设定理2.1的条件成立, 且
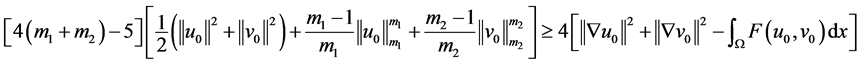 (3.11)
(3.11)
则问题(1.1)~(1.4)的弱解 必在某有限时刻
必在某有限时刻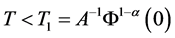 爆破,即
爆破,即
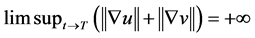
证明:方程(1.1),(1.2)两边分别同乘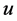 和
和 ,然后关于x积分并相加,得
,然后关于x积分并相加,得
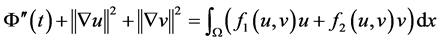 (3.12)
(3.12)
方程(1.1),(1.2)两边分别同乘 和
和 ,然后关于x积分并相加,得
,然后关于x积分并相加,得
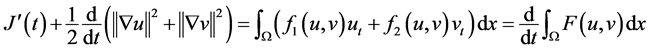 (3.13)
(3.13)
(3.13)关于t积分得
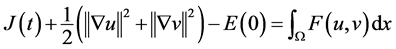 (3.14)
(3.14)
再利用条件(A1)得
 (3.15)
(3.15)
(3.12)结合(3.15),并用到 ,得
,得
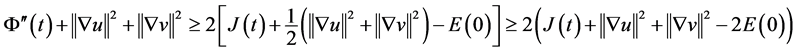
即
 (3.16)
(3.16)
注意到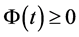 得
得
 (3.17)
(3.17)
利用引理3.1,得
 (3.18)
(3.18)
其中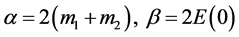 。
。
如果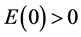 ,由(3.1),(3.6)和(3.11)知
,由(3.1),(3.6)和(3.11)知
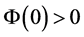 ,
,  ,
, 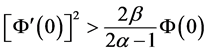
于是,由引理2.2得结论。如果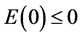 ,取
,取 ,则(3.18)变为
,则(3.18)变为
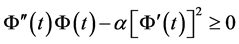
于是,由标准的凸性引理得结论。
文章引用
苏 璟,齐龙飞,呼青英, (2015) 多重非线性抛物方程组解的爆破
Blowup of Solutions for a Class of Doubly Nonlinear Parabolic Equations. 理论数学,02,59-65. doi: 10.12677/PM.2015.52009
参考文献 (References)
- 1. Kalashnikov, A.S. (1987) Some problem of the qualitative theory of nonlinear degenerate second-order parabolic equa-tions. Russian Mathematical Surveys, 42, 169-222.
- 2. Lions, J.L. (1969) Quelques methodes de resolution desprob-lemes aux limites non lineaires. Dunod, Paris.
- 3. Ivanov, A.V. (1993) Quasilinear parabolic equations admitting double degeneracy. St. Petersburg Mathematical Journal, 4, 1153-1168.
- 4. Laptev, G.I. (1997) Solvability of second-order quasilinear parabolic equations with double degeneration. Siberian Mathematical Journal, 38, 1160-1177.
- 5. Tsutsumi, M. (1988) On solution of some doubly nonlinear parabolic equations with absorption. Journal of Mathematical Analysis and Applications, 132, 187-212.
- 6. Laptev, G.I. (2000) Evolution equations with monotone operator and functional nonlinearity at the time derivative. Sbornik: Mathematics, 19, 1301-1322.
- 7. Eden, A. and Rakotoson, J.M. (1994) Exponential attractors for a doubly nonlinear equation. Journal of Mathematical Analysis and Applications, 185, 321-339
- 8. Eden, A., Michaux, B. and Rakotoson, J.M. (1991) Doubly nonlinear parabolic type equations as dynamical systems. Journal of Dynamics and Differential Equations, 3, 87-131
- 9. Miranville, A. (2006) Finite dimensional global attractor for a class of doubly nonlinear parabolic equation. Central European Journal of Mathematics, 4, 163-182.
- 10. Miranville, A. and Zelik, S. (2007) Finite-dimensionality of attractors for degenerate equations of elliptic–parabolic type. Nonlinearity, 20, 1773-1797.
- 11. Ouardi, H.E. and Hachimi, A.E. (2001) Existence and attractors of solutions for nonlinear parabolic systems. Electronic Journal of Qualitative Theory of Differential Equations, 2001, 1-16.
- 12. Ouardi, H.E. and Hachimi, A.E. (2006) Attractors for a class of doubly nonlinear parabolic systems. Electronic Journal of Qualitative Theory of Differential Equations, 2006, 1-15.
- 13. Levine, H.A. (1973) Some nonexistence and instability theorems for solutions of formally parabolic equations of the form . Archive for Rational Mechanics and Analysis, 51, 371-386.
- 14. Levine, H.A., Park, S.R. and Serrin, J.M. (1998) Global existence and nonexistence theorems for quasilinear evolution equations of formally parabolic type. Journal of Differential Equations, 142, 212-229.
- 15. Iami, T. and Mochizuki, K. (1991) On the blowup of solutions for quasilinear degenerate parabolic equations. Publications of the Research Institute for Mathematical Sciences (Kyoto University), 27, 695-709.
- 16. Levine, H.A. and Sacks, P.E. (1984) Some existence and nonexistence theorems for solutions of degenerate parabolic equations. Journal of Differential Equations, 52, 135-161.
- 17. Levine, H.A. and Payne, L.E. (1974) Nonexistence theorems for the heat equations with nonlinear boundary conditions and for the porous medium equation backward in time. Journal of Differential Equations, 16, 319-334.
- 18. Sacks, P.E. (1983) Continuity of solutions of a singular parabolic equation. Nonlinear Analysis, TMA, 7, 387-409.
- 19. Zhang, H.L. (2008) Blow-up solutions and global solutions for nonlinear parabolic problems. Nonlinear Analysis, 69, 4567-4575.
- 20. Ding, J.T. and Guo, B.Z. (2009) Global and blowup solutions for nonlinear parabolic equations with a gradient term. Houston Journal of Mathematics, 37, 1265-1277.
- 21. Ding, J.T. and Guo, B.Z. (2011) Blow-up solution of nonlinear reaction-diffusion equations under boundary feedback. Journal of Dynamical and Control Systems, 17, 273-290.
- 22. Ding, J.T. (2013) Global and blow-up solutions for nonlinear parabolic equations with Robin boundary conditions. Computers and Mathematics with Applications, 65, 1808-1822.
- 23. Korpusov, M.O. and Sveshnikov, A.G. (2011) Blowup in nonlinear Sobolev type equation. De Gruyter, Berlin/New York.
- 24. Korpusov, M.O. (2013) Solution blow-up for a class of parabolic equations with double nonlinearity. Sbornik: Mathematics, 204, 323-346.
- 25. Hachimi, A.E. and Ouardi, H.E. (2002) Existence and of regularity a global attractor for doubly nonlinear parabolic equations. Electronic Journal of Differential Equations, 2002, 1-15.
- 26. Ouardi, H.E. (2007) On the finite dimension of attractors of doubly nonlinear parabolic systems with l-trajectories. Archivum Mathematicum, 43, 289-303.
- 27. Agre, K. and Rammaha, M.A. (2006) Systems of nonlinear wave equations with damping and source terms. Differential and Integral Equations, 19, 1235-1270.
- 28. Korpusov, M.O. (2012) Blow-up for a positive-energy solution of model wave equations in nonlinear dynamics. Theoretical and Mathematical Analysis, 171, 421-434.