Pure Mathematics
Vol.06 No.01(2016), Article ID:16845,5
pages
10.12677/PM.2016.61006
Several Inequalities Related to Circumcentre Lines for n-Dimensional Simplexes
Le Zhang, Weidong Wang
Department of Mathematics, China Three Gorges University, Yichang Hubei

Received: Nov. 25th, 2015; accepted: Jan. 21st, 2016; published: Jan. 28th, 2016
Copyright © 2016 by authors and Hans Publishers Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/



ABSTRACT
The essay has introduced the notion of circumcentre line, and has obtained several inequalities related to circumscribed sphere radius in an n-dimensional simplex by making use of it.
Keywords:n-Dimensional Simplex, Circumcentre Line, Circumscribed Sphere Radius

n维单形中与外心线相关的几个不等式
章乐,王卫东
三峡大学理学院数学系,湖北 宜昌

收稿日期:2015年11月25日;录用日期:2016年1月21日;发布日期:2016年1月28日

摘 要
本文引入了n维单形外心线的概念,并应用它建立了几个与n维单形外接球半径有关的不等式。
关键词 :n维单形,外心线,外接球半径

最近,文[1] 引入了与三角形高线,内角平分线和中线平行的一个新概念——三角形的外心线。结合这个新概念,文 [1] [2] 通过类比三角形中与高线、内角平分线和中线相关的不等式,建立了如下与三角形外心线相关的不等式。
定理A ( [2] ). 在锐角DABC中,设三条外心线的长为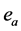 ,
, ,
,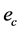 ,外接圆半径为
,外接圆半径为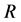 。
。
若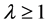 ,则
,则
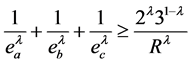 ; (1)
; (1)
若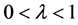 ,则不等式(1)是逆向的。当
,则不等式(1)是逆向的。当 时,不等式(1)和它的逆形式中等号成立当且仅当DABC为正三角形;当
时,不等式(1)和它的逆形式中等号成立当且仅当DABC为正三角形;当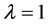 时,(1)是恒等式。
时,(1)是恒等式。
定理B ( [2] ). 在锐角DABC中,设三条外心线的长为 ,
,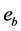 ,
,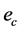 ,外接圆半径为
,外接圆半径为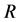 。若
。若 ,则
,则
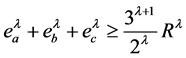 ,
,
等号成立当且仅当DABC为正三角形。
定理C ( [1] ). 在锐角DABC中,设三条外心线的长为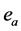 ,
,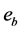 ,
, ,外接圆半径为
,外接圆半径为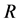 ,则有
,则有
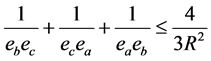 ,
,
等号成立当且仅当DABC为正三角形。
关于三角形中与外心线相关的几何不等式研究,还可以参见文 [3] [4] 。
在文 [5] 中,段继艳和王卫东把定理A和定理C中的不等式推广到四面体中,建立了四面体中与外心线相关的不等式。本文将上述不等式推广到n维单形中,得到了n维单形中与外心线相关的不等式。这里,我们先给出n维单形外心线的概念如下:
定义1. 设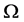 为n维欧氏空间
为n维欧氏空间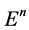 中的单形,其顶点集为
中的单形,其顶点集为 ,过n维单形
,过n维单形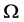 的一个顶点
的一个顶点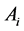 和它的外接球的球心的直线,与顶点
和它的外接球的球心的直线,与顶点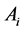 所对面所在的平面相交于一点,该顶点
所对面所在的平面相交于一点,该顶点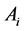 与交点之间的线段就叫做n维单形
与交点之间的线段就叫做n维单形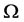 中过顶点
中过顶点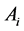 的一条外心线。
的一条外心线。
在n维单形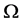 中,我们记过顶点
中,我们记过顶点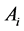 的外心线长为
的外心线长为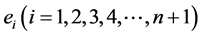 ,
,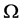 的外接球的半径为
的外接球的半径为 。结合定义1,我们建立了如下n维单形中与外心线相关的不等式。
。结合定义1,我们建立了如下n维单形中与外心线相关的不等式。
定理1. 在n维单形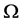 中,设外接球的球心O在
中,设外接球的球心O在 的内部,若
的内部,若 ,则
,则
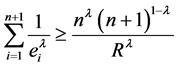 ; (2)
; (2)
若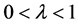 ,则不等式(2)是逆向的。等号成立当
,则不等式(2)是逆向的。等号成立当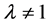 时当且仅当
时当且仅当 中诸外心线长
中诸外心线长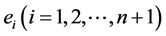 都相等;当
都相等;当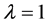 时,(2)是恒等式。
时,(2)是恒等式。
定理2. 在n维单形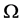 中,设外接球的球心O在
中,设外接球的球心O在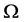 的内部,若
的内部,若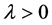 ,则
,则
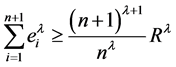 , (3)
, (3)
等号成立当且仅当 中外心线长
中外心线长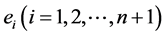 都相等。
都相等。
定理3. 在n维单形 中,设外接球的球心O在
中,设外接球的球心O在 的内部,则有
的内部,则有
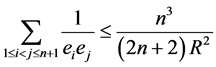 ,(4)
,(4)
等号成立当且仅当在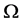 中外心线长
中外心线长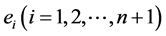 都相等。
都相等。
下面我们给出上述定理1~3的证明。
引理1 (Holder不等式[6] ). 设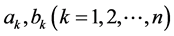 均为正实数,
均为正实数,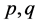 为实数,且
为实数,且 ,若
,若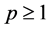 ,则有
,则有
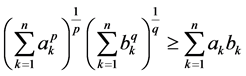 , (5)
, (5)
等号成立当且仅当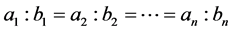 ;若
;若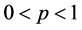 或
或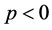 ,则不等式(5)是逆向的。
,则不等式(5)是逆向的。
定理1的证明. 由于外接球的球心O在n维单形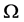 的内部,为此设n维单形
的内部,为此设n维单形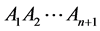 ,
,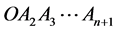 ,
,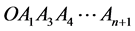 ,
, ,
, 的体积分别为
的体积分别为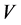 ,
,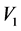 ,
,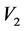 ,
, ,
,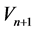 ,则
,则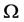 的体积为
的体积为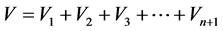 。又设
。又设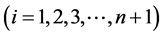
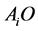 的延长线交
的延长线交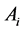 所对面于点
所对面于点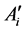 ,则知
,则知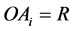 ,
,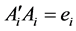 。由于
。由于
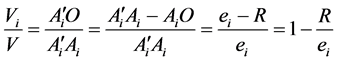 ,
,
于是令 ,则有
,则有 ,且
,且
 。 (6)
。 (6)
因而可得
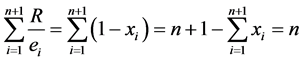 ,
,
即
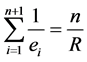 。 (7)
。 (7)
因此,利用(7)和Holder不等式(5)知:当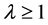 时有
时有
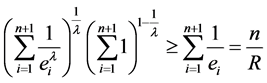 。(8)
。(8)
由此可得不等式(2)。
同理,当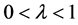 时,利用Holder不等式(5)的逆形式,可得不等式(8)的逆形式,即得不等式(2)的逆为真。
时,利用Holder不等式(5)的逆形式,可得不等式(8)的逆形式,即得不等式(2)的逆为真。
显然,由(7)知,当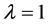 时,(2)中等号成立;当
时,(2)中等号成立;当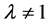 时,根据Holder不等式取等号的条件知,不等式(8)和它的逆形式中等号成立当且仅当诸外心线长
时,根据Holder不等式取等号的条件知,不等式(8)和它的逆形式中等号成立当且仅当诸外心线长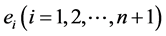 相等,即知不等式(2)和它的逆形式中等号成立当且仅当
相等,即知不等式(2)和它的逆形式中等号成立当且仅当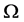 的诸外心线长
的诸外心线长 都相等。定理1证毕。
都相等。定理1证毕。
定理2的证明. 当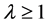 时,由Holder不等式(5)有
时,由Holder不等式(5)有
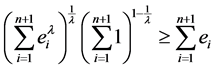 , (9)
, (9)
且根据Holder不等式取等号的条件知,(9)中等号成立当且仅当诸外心线长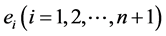 都相等。
都相等。
又由Holde不等式(5)有
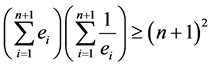 ,
,
由此利用(7)可得
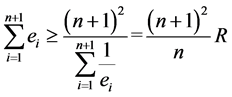 , (10)
, (10)
且等号成立当且仅当诸外心线长 都相等。
都相等。
于是由(9)和(10)知
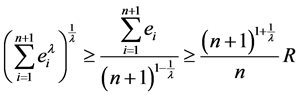 ,
,
即有
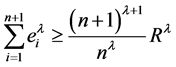 。
。
此即为不等式(3)。根据不等式(9)和(10)中取等号的条件知:不等式(3)中等号成立当且仅当诸外心线长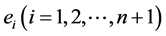 都相等。
都相等。
当 时,由不等式(2)的逆和Holder不等式(5)有
时,由不等式(2)的逆和Holder不等式(5)有
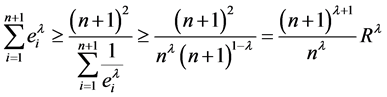 ,
,
由此仍然得到不等式(3)。定理2证毕。
定理3的证明. 由(6)知:
 , (11)
, (11)
又
 , (12)
, (12)
等号成立当且仅当诸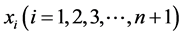 都相等。
都相等。
于是知
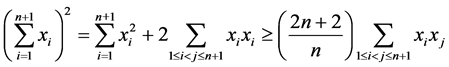 ,
,
由此结合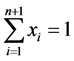 ,则有
,则有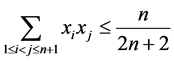 。将其代入(11)中有
。将其代入(11)中有
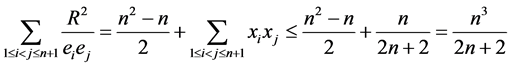 。
。
因此即得不等式(4)。
由不等式(12)取等号的条件知,不等式(4)中等号成立当且仅当诸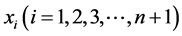 相等,由(6)即知诸
相等,由(6)即知诸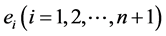 相等,定理3证毕。
相等,定理3证毕。
利用Holder不等式(5)和不等式(4),易知
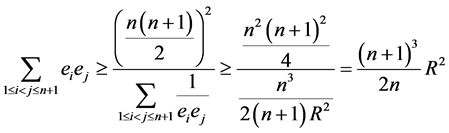 。
。
根据Holder不等式(5)取等号的条件知,上述不等式中等号成立当且仅当诸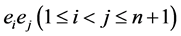 相等,即诸
相等,即诸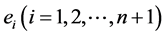 相等。由此可得如下结论:
相等。由此可得如下结论:
推论1. 在n维单形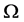 中,设外接球的球心
中,设外接球的球心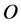 在
在 的内部,则有
的内部,则有
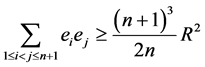 ,
,
等号成立当且仅当n维单形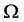 中外心线长
中外心线长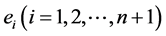 都相等。
都相等。
基金项目
国家自然科学基金项目(11371224);三峡大学“求索”大学生创新活动计划重点项目。
文章引用
章 乐,王卫东. n维单形中与外心线相关的几个不等式
Several Inequalities Related to Circumcentre Lines for n-Dimensional Simplexes[J]. 理论数学, 2016, 06(01): 37-41. http://dx.doi.org/10.12677/PM.2016.61006
参考文献 (References)
- 1. 贺小刚, 吴恒, 王卫东. 三角形中一类新的几何不等式[J]. 数学通报, 2012, 51(2): 62-63.
- 2. 陈贝贝, 王卫东. 关于三角形外心线的几个不等式[J]. 数学通报, 2012, 51(10): 58-60.
- 3. 赵龙潮, 王卫东. 涉及三角形外心线的一类几何不等式[J]. 数学通报, 2012, 51(7): 55-57.
- 4. 刘合勇, 邓秀方, 王卫东. 联系三角形外心线的几个不等式[J]. 中学数学教学参考, 2014, 1-2(下旬): 127-129.
- 5. 段继艳, 王卫东. 四面体中与外心线相关的几个不等式[J]. 数学通报, 2014, 53(7): 57-58.
- 6. 匡继昌. 常用不等式[M]. 第4版. 济南: 山东科技技术出版社, 2010.