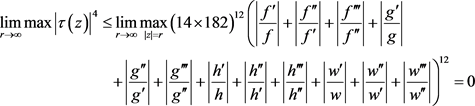Pure Mathematics
Vol.08 No.01(2018), Article ID:23399,7
pages
10.12677/PM.2018.81006
The Study of Meromorphic Function Solution of Function Equation of
E Liang
School of Mathematics, Yunnan Normal University, Kunming Yunnan
Received: Dec. 20th, 2017; accepted: Jan. 2nd, 2018; published: Jan. 12th, 2018

ABSTRACT
This paper proves that nonconstant meromorphic function
in the pole is not more than a single pole with public, and
, the solution of Fermat function equations
does not exist.
Keywords:Fermat Type Functional Equation, Meromorphic Functions, Order of Growth

函数方程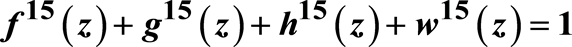 的亚纯函数解的研究
的亚纯函数解的研究
梁娥
云南师范大学数学学院,云南 昆明
收稿日期:2017年12月20日;录用日期:2018年1月2日;发布日期:2018年1月12日

摘 要
本文证明了若非常数亚纯函数
的极点中至多只有一个是公共单级极点,且
,则 一定不是Fermat型函数方程
一定不是Fermat型函数方程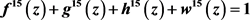 的解。
的解。
关键词 :Fermat型函数方程,亚纯函数,增长极

Copyright © 2018 by author and Hans Publishers Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/


1. 引言及主要结果
本文使用Nevanlinna值分布理论的基本结果及其标准记号 [1] 。我们考虑如下费马型函数方程:
(1)
的非常数亚纯函数解,G.G.GUNDERSEN在文献 [2] 中给出了当 时,函数方程(1)的超越亚纯函数解的例子。
时,函数方程(1)的超越亚纯函数解的例子。
我们也知道,用Cartan定理易证
时,函数方程(1)不存在非常数亚纯函数解,那么就存在一个公开性的问题;当
时,函数方程(1)是否存在非常数亚纯函数解?
基于这个问题,本文我们将研究当
时,函数方程(1)的亚纯函数解的状况。
之前苏敏、李玉华 [3] 证明了:费马型函数方程
无级小于1的非常数整函数解以及费马型函数方程
不存在级小于1的非常数亚纯函数解。
加上直接研究费马型函数方程
的非平凡亚纯解较难,从而在引入级小于1的条件的启发下,本文得到了以下结果:
定理1:若非常数亚纯函数
的极点中至多只有一个是公共单级极点,且
,则
一定不是Fermat型函数方程
的解。
2. 几个辅助结果
引理1 [4] :设函数
于开平面亚纯, 为正整数,则
与
有相同的级与下级。
为正整数,则
与
有相同的级与下级。
引理2 [5] :若 是非常数亚纯函数,且
是非常数亚纯函数,且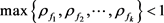 ,那么
,那么
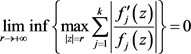 .
.
特别的,若非常数亚纯函数
的级
,则有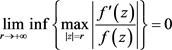 。
。
引理3 [6] :若
为区域
上
个亚纯函数,且
线性无关,那么
的Wronskian行列式
.
引理4:若非常数亚纯函数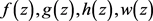 无公共单级极点,且
满足函数方程
无公共单级极点,且
满足函数方程
, (2)
令
,
其中
,(
为非常数亚纯函数)。
则
是整函数。
引理4的证明:
因为非常数亚纯函数
满足函数方程(2),则
线性无关。事实上,若
线性相关,则
中至少有一个为常数函数,矛盾。结合引理3,则有:
(3)
其中
;
,(其中
为非常数亚纯函数)。
故
。此外,结合函数方程
以及伏朗斯基行列式的特点可得到:
(4)
其中
,(其中
为非常数亚纯函数)。
由(3)、(4)可得
(5)
同理,可得:
 (6)
(6)
 (7)
(7)
(8)
实际上,因为定义的
为涉及
的行列式,则若 有极点,其极点只会在
的极点处产生,设
为
的
重极点,设
在
处的洛朗展开式为
有极点,其极点只会在
的极点处产生,设
为
的
重极点,设
在
处的洛朗展开式为
,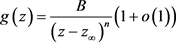 ,
,
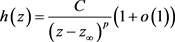 ,
,
,
,
由(2)式成立可知,若继设
,根据等式两边对称性,则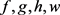 中至少有两个亚纯函数的极点重数是相同的,不妨设
。根据(5)式,
中至少有两个亚纯函数的极点重数是相同的,不妨设
。根据(5)式,
, (9)
其中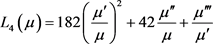 ,(其中
为非常数亚纯函数)。
,(其中
为非常数亚纯函数)。
而行列式
(10)
通过代换
的洛朗展开式进行运算可得,上面的行列式实际可以表示为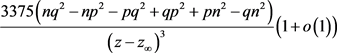 ,同样通过代换
的洛朗展开式计算可得到
(其中
是常数),从而由(9)式可知,当
,同样通过代换
的洛朗展开式计算可得到
(其中
是常数),从而由(9)式可知,当
(*)
时,
不是
的极点。下面我们将分类讨论如下:
I) 若
,
易见此情况下满足(*)式,故此时
不是
的极点。
II) 若 ,
,
此情况下
,也是符合(*)式,故此时
不是
的极点。
III) 若
,
此情况下
,也是符合(*)式,故此时
不是
的极点。
IV)
,
此情况下
,符合(*)式,故此时
不是
的极点。
V)
,
即在
处函数 解析而另外三个函数不解析,该情况下
,显然符合(*)式,故此时
不是
的极点。
解析而另外三个函数不解析,该情况下
,显然符合(*)式,故此时
不是
的极点。
VI)
,
不妨设
为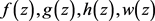 的公共单级极点,则
在0处的洛朗展开式为
的公共单级极点,则
在0处的洛朗展开式为
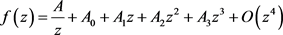 ,
,
,
,
,
。
通过计算可知(10)式在公共单级极点处可能产生一阶极点,从而
在公共单级极点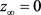 处可能不解析。
处可能不解析。
综上所述,若非常数亚纯函数
无公共单级极点,则
为整函数,引理4得证。
3. 定理1的证明
记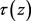 为引理4中所定义的行列式,由引理4的证明过程知
为引理4中所定义的行列式,由引理4的证明过程知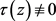 ,且由(5)、(6)、(7)、(8)可得
,且由(5)、(6)、(7)、(8)可得
其中
;
(
为非常数亚纯函数)。
从而有
(**)
因为非常数亚纯函数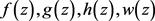 满足费马型函数方程(2),所以
满足费马型函数方程(2),所以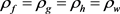 ,又
,所以有
,下面分两种情况来讨论:
,又
,所以有
,下面分两种情况来讨论:
情况一:若非常数亚纯函数
无公共单级极点,则采用反证法,假设函数方程(2)存在级小于
的非常数亚纯函数解,根据引理1知
,
,
,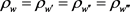 。
。
于是
,又根据引理2和(**)式有
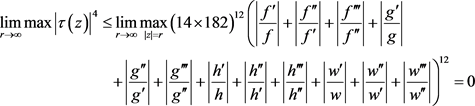
再结合引理4的结论知
为整函数,则
,这与
矛盾。
情况二:若非常数亚纯函数
仅有一个公共单级极点
,不妨设
,由函数方程(2)有
成立,兹令
则有
,且
,而非常数亚纯函数
仅有一个公共单重极点0,则
无公共单级极点,此时可转化为同情况一一样的讨论亦得出矛盾。
综上,定理1得证。
参考文献 (References)
[1] 杨乐. 值分布论及其新研究[M]. 北京: 科学出版社, 1982.
[2] Gundersen, G.G. (2003) Complex Functional Equations.
[3] 苏敏, 李玉华. 关于函数方程非平凡亚纯解的研究[J]. 云南师范大学学报: 自然科学版, 2009, 29(2): 44.
[4] 仪洪勋, 杨重骏. 亚纯函数唯一性理论[M]. 北京: 科学出版社, 1995.
[5] Li, Y.H. (2000) Uniqueness Theorems for Meromorphic Functions of Order Less than One. Northeastern Mathematical Journal, 16, 411-416.
[6] 顾永兴, 庞学诚, 方明亮. 正规族理论及其应用[M]. 北京: 科学出版社, 2007.


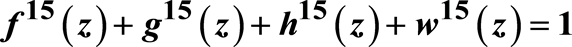 的亚纯函数解的研究
的亚纯函数解的研究 

 一定不是Fermat型函数方程
一定不是Fermat型函数方程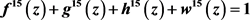 的解。
的解。


 时,函数方程(1)的超越亚纯函数解的例子。
时,函数方程(1)的超越亚纯函数解的例子。 为正整数,则
与
有相同的级与下级。
为正整数,则
与
有相同的级与下级。 是非常数亚纯函数,且
是非常数亚纯函数,且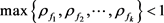 ,那么
,那么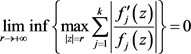 .
.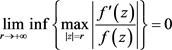 。
。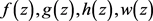 无公共单级极点,且
满足函数方程
无公共单级极点,且
满足函数方程 (6)
(6) (7)
(7) 有极点,其极点只会在
的极点处产生,设
为
的
重极点,设
在
处的洛朗展开式为
有极点,其极点只会在
的极点处产生,设
为
的
重极点,设
在
处的洛朗展开式为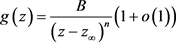 ,
,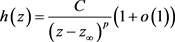 ,
,
,
,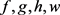 中至少有两个亚纯函数的极点重数是相同的,不妨设
。根据(5)式,
中至少有两个亚纯函数的极点重数是相同的,不妨设
。根据(5)式,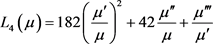 ,(其中
为非常数亚纯函数)。
,(其中
为非常数亚纯函数)。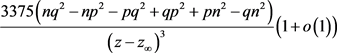 ,同样通过代换
的洛朗展开式计算可得到
(其中
是常数),从而由(9)式可知,当
,同样通过代换
的洛朗展开式计算可得到
(其中
是常数),从而由(9)式可知,当 ,
, 解析而另外三个函数不解析,该情况下
,显然符合(*)式,故此时
不是
的极点。
解析而另外三个函数不解析,该情况下
,显然符合(*)式,故此时
不是
的极点。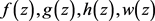 的公共单级极点,则
在0处的洛朗展开式为
的公共单级极点,则
在0处的洛朗展开式为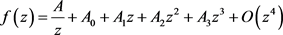 ,
,
,
,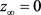 处可能不解析。
处可能不解析。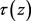 为引理4中所定义的行列式,由引理4的证明过程知
为引理4中所定义的行列式,由引理4的证明过程知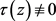 ,且由(5)、(6)、(7)、(8)可得
,且由(5)、(6)、(7)、(8)可得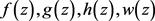 满足费马型函数方程(2),所以
满足费马型函数方程(2),所以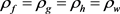 ,又
,所以有
,下面分两种情况来讨论:
,又
,所以有
,下面分两种情况来讨论: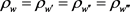 。
。