弱Gorenstein X-投(内)射模 Weak Gorenstein X-Projective (Injective) Modules

doi:10.12677/PM.2022.124058

Pure Mathematics
Vol. 12 No. 04 ( 2022 ), Article ID: 50150 , 7 pages
10.12677/PM.2022.124058

弱Gorenstein X-投(内)射模

武新文

●How to Cite this Article

敦煌市第二中学，甘肃敦煌

收稿日期：2022年3月2日；录用日期：2022年4月5日；发布日期：2022年4月12日

摘要

引入弱Gorenstein X-投(内)射模，讨论其基本同调性质，证明在任意环R上，若lD(R) ≤ 1，则Gorenstein X-投(内)射模类、弱Gorenstein X-投(内)射模类、Gorenstein投(内)射模类和弱Gorenstein投(内)射模类是同一个类。

关键词

弱Gorenstein X-投(内)射模，wGXI-封闭环

Weak Gorenstein X-Projective (Injective) Modules

Xinwen Wu

Dunhuang No. 2 Middle School, Dunhuang Gansu

Received: Mar. 2^nd, 2022; accepted: Apr. 5^th, 2022; published: Apr. 12^th, 2022

ABSTRACT

Weak Gorenstein X-projective (injective) modules are introduced. The homological properties of the two types of modules are investigated. It is proved that on the ring R, if lD(R) ≤ 1, then the class of Gorenstein X-projective (injective) modules, the class of weak Gorenstein X-projective (injective) modules, the class of Gorenstein projective (injective) modules and the class of weak Gorenstein projective (injective) modules are the same class.

Keywords:Weak Gorenstein X-Projective (Injective) Module, wGXI-Closed Ring

This work is licensed under the Creative Commons Attribution International License (CC BY 4.0).

http://creativecommons.org/licenses/by/4.0/

1. 引言

1994年，Fay等人引入X-投(内)射模的概念，研究了其同调性质 [1]。1995年，Enochs等人在一般环上引入Gorenstein投(内)射模的概念 [2]。随后，以Gorenstein投(内)射模为对象的Gorenstein相对同调代数得到了广大学者的青睐。2007年，Bennis等人引入强Gorenstein 投(内)射模的概念 [3]。2013年，高增辉引入弱Gorenstein投(内)射模 [4]。2014年，Umamaheswaran等人引入Gorenstein X-投(内)射模的概念 [5]。同年，陈文静等人引入弱Gorenstein FP-内射模的概念，讨论了凝聚环上FP-内射模类、Gorenstein FP-内射模类和弱Gorenstein FP-内射模类三者之间的联系 [6] [7]。2021年，袁倩等人引入弱Gorenstein FC-投射模的概念，讨论了任意环上FC-投射模类、Gorenstein FC-投射模类、强Gorenstein FC-投射模类、弱Gorenstein FC-投射模类和强泛Gorenstein FC-投射模类五者之间的联系，并利用弱Gorenstein FC-投射模对右Gorenstein FC-半单环进行了刻画 [8]。

受以上文献的启发，我们利用X-投(内)射模，引入弱Gorenstein X-投(内)射模的概念，讨论其同调性质，并证明当lD(R) ≤ 1时，模类Gorenstein投(内)射模类、Gorenstein X-投(内)射模类、弱Gorenstein投(内)射模类和弱Gorenstein X-投(内)射模类是同一个类。

本文中所提到的环均指有单位元的结合环。模均指酉模，除非特别说明，R-模指左R-模。本文中，我们用R-Mod表示左R-模范畴；用P (I, GP, GI, SGP, SGI, wGP, wGI, GXP, GXI)表示投射R-模类(内射R-模类，Gorenstein投射R-模类，Gorenstein内射R-模类，强Gorenstein投射R-模类，强Gorenstein内射R-模类，弱Gorenstein投射R-模类，弱Gorenstein 内射R-模类，Gorenstein X-投射R-模类，Gorenstein X-内射R-模类)；用pd(M)和id(M)表示R-模M的投射维数和内射维数；用lD(R)表示环R的左整体维数。 $ℕ$ 表示自然数集。未交待的概念和符号，参考文献 [5] [8] [9] [10]。

全文共分为四部分：第一节引言；第二节罗列本文所需概念和基本事实；第三节引入弱Gorenstein X-投(内)射模，讨论其基本同调性质；第四节利用模的X-投(内)射维数，证明当lD(R) ≤ 1时，模类Gorenstein 投(内)射模类、Gorenstein X-投(内)射模类、弱Gorenstein投(内)射模类和弱Gorenstein X-投(内)射模类是同一个类。

2. 预备知识

定义2.1 [1] 设X是R-模类，称R-模M是X-投射模，如果对任意 $N \in X$ ， ${Ext}_{R}^{1} (M, N) = 0$ 。我们将X-投射模记作XP。对偶地，可定义XI。

定义2.2 [2] 称投射R-模的正合列 $P = \dots \to P_{1} \to P_{0} \to P_{- 1} \to P_{- 2} \to \dots$ 是完全投射分解，如果对任意投射R-模Q，序列 ${Hom}_{R} (P, Q)$ 正合。称R-模M是Gorenstein投射模，如果存在一个完全投射分解 $P$ 使得 $M ≅ Ker (P_{- 1} \to P_{- 2})$ 。我们将Gorenstein投射模记作GP。对偶地，可定义GI。

定义2.3 [3] 称R-模M是强Gorenstein投射模，如果存在投射R-模的正合列 $Θ = \dots \to P \to P \to P \to P \to \dots$ ，使得 $M ≅ Ker (P \to P)$ ，并且对任意投射R-模Q，序列 ${Hom}_{R} (Θ, Q)$ 正合。我们将强Gorenstein投射模记作SGP。对偶地，可定义SGI。

定义2.4 [4] 称R-模M是弱Gorenstein投射模，如果存在投射R-模的正合列 $Θ = \dots \to P_{1} \to P_{0} \to P^{0} \to P^{1} \to \dots$ ，使得 $M ≅ Ker (P^{0} \to P^{1})$ 。此时，称序列 $Θ$ 是M的弱完全投射分解。我们将弱Gorenstein投射模记作wGP。对偶地，可定义wGI。

定义2.5 [5] 设X是R-模类，称R-模M是Gorenstein X-投射模，如果存在投射模R-模的正合列 $Φ = \dots \to P_{1} \to P_{0} \to P^{0} \to P^{1} \to \dots$ ，使得 $M ≅ Ker (P^{0} \to P^{1})$ ，并且对任意 $Q \in X$ ，序列 ${Hom}_{R} (Φ, Q)$ 正合。我们将Gorenstein X-投射模记作GXP。对偶地，可定义GXI。

定义2.6 [9] 称R-模类X是投射可解类，如果 $P \subseteq X$ ，且对任意X中的正合列 $0 \to X^{'} \to X \to X^{″} \to 0$ ，其中 $X^{″} \in X$ ，则 $X^{'} \in X \Leftrightarrow X \in X$ 。对偶地，可定义内射可解类。

3. 弱Gorenstein X-投射模

本部分我们引入弱Gorenstein X-投(内)射模，讨论其基本同调性质。

定义3.1 设X是R-模类，称R-模M是是弱Gorenstein X-投射模，如果存在正合列

$Ψ = \dots \to P_{1} \to P_{0} \to P^{0} \to P^{1} \to \dots$ ，

其中 $P_{i}, P^{i} \in X P (i \in ℕ)$ ，使得 $M ≅ Ker (P^{0} \to P^{1})$ 。此时，称正合列 $Ψ$ 是M的弱完全X-投射分解。

对偶地，称R-模M是是弱Gorenstein X-内射模，如果存在正合列

$Ω = \dots \to E_{1} \to E_{0} \to E^{0} \to E^{1} \to \dots$ ，

其中 $E_{i}, E^{i} \in X I (i \in ℕ)$ ，使得 $M ≅ Ker (P^{0} \to P^{1})$ 。此时，称正合列 $Ω$ 是M的弱完全X-内射分解。

我们将弱Gorenstein X-投(内)射R-模类记为wGXP(wGXI)。

关于定义，我们注意到

注记3.2 1) $P \subseteq X P \subseteq w G X P$ ； $I \subseteq X I \subseteq w G X I$ ；

2) $P \subseteq G X P \subseteq w G X P$ ； $I \subseteq G X I \subseteq w G X I$ ；

3) 由对称性可知，定义3.1中的正合列 $Ψ$ ( $Ω$ )中所有同态的像、核和余核都是弱Gorenstein X-投(内)射模；

4) wGXP(wGXI)关于直和(直积)封闭。

例3.3 1) 当X = R-Mod时，wGXP = wGP，wGXI = wGI；

2) 当X是有限表示R-模类时，弱Gorenstein X-内射模就是文献 [6] 中的弱Gorenstein FP-内射模；

3) 当X是有限余表示R-模类时，弱Gorenstein X-投射模就是文献 [8] 中的弱Gorenstein FC-投射模。

下面首先给出弱Gorenstein X-投射模的一些等价刻画，关于弱Gorenstein X-内射模，均有对偶结论。

命题3.4 设M是一R-模，则以下等价：

1) $M \in w G X P$ ；

2) 存在正合列 $0 \to M \to P^{0} \to P^{1} \to \dots$ ，其中 $P^{i} \in X P (i \in ℕ)$ ；

3) 存在正合列 $0 \to M \to P \to N \to 0$ ，其中 $P \in X P$ ， $N \in w G X P$ 。

证明 (1) $\Rightarrow$ (2)，(1) $\Rightarrow$ (3)由定义3.1易得。

(3) $\Rightarrow$ (2)因为 $N \in w G X P$ ，所以存在N的弱完全X-投射分解

$Ψ = \dots \to P_{1} \to P_{0} \to P^{0} \to P^{1} \to \dots$ ，

其中 $P_{i}, P^{i} \in X P (i \in ℕ)$ ，使得 $N ≅ Ker (P^{0} \to P^{1})$ ，故存在正合列 $0 \to M \to P \to P^{0} \to P^{1} \to \dots$ ，其中P和 $P^{i} \in X P (i \in ℕ)$ 。

(2) $\Rightarrow$ (1)任取M的一个投射分解 $\dots \to P_{1} \to P_{0} \to M \to 0$ ，与条件中序列首尾相接就得到M的弱完全X-投射分解

$Ψ = \dots \to P_{1} \to P_{0} \to P^{0} \to P^{1} \to \dots$ ，

使得 $M ≅ Ker (P^{0} \to P^{1})$ ，故 $M \in w G X P$ 。

下面我们证明wGXP是投射可解类，并且关于直和项封闭。

命题3.5 设R是环，则wGXP关于扩张封闭当且仅当wGXP是投射可解类。

证明( $\Leftarrow$ )显然。

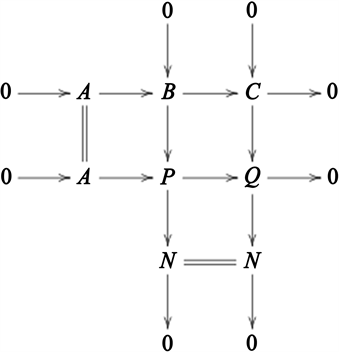
( $\Rightarrow$ )设 $0 \to A \to B \to C \to 0$ 是R-模的正合列，只需证当 $B, C \in w G X P$ 时, $A \in w G X P$ 即可。因为 $B \in w G X P$ ，所以由命题3.4可知存在正合列 $0 \to B \to P \to N \to 0$ ，其中 $P \in X P$ ， $N \in w G X P$ 。考虑推出图

因为 $C, N \in w G X P$ ，所以 $Q \in w G X P$ 。对中间行用命题3.4可得 $A \in w G X P$ 。

定义3.6 称环R是左wGXP封闭环，如果wGXP关于扩张封闭。

推论3.7 设R是左wGXP封闭环，则wGXP关于直和项封闭。

证明由文献( [9]，命题1.4)易得。

命题3.8 设R是左wGXP封闭环， $0 \to N \to M \to P \to 0$ 是R-模的正合列，其中 $P \in P$ ，则 $M \in w G X P$ $\Leftrightarrow$ $N \in w G X P$ 。

证明由注记3.2和推论3.7易得。

引理3.9 XP关于扩张与直和项封闭。

证明设X是R-模类， $0 \to A \to B \to C \to 0$ 是R-模的正合列，其中 $A, C \in X P$ 。下证 $B \in X P$ 。任取 $N \in X$ ，存在长正合列 $\dots \to {Ext}_{R}^{1} (C, N) \to {Ext}_{R}^{1} (B, N) \to {Ext}_{R}^{1} (A, N) \to \dots$ 。因为 $A, C \in X P$ ，所以 ${Ext}_{R}^{1} (A, N) = 0$ ， ${Ext}_{R}^{1} (C, N) = 0$ 。于是 ${Ext}_{R}^{1} (B, N) = 0$ ，故 $B \in X P$ ，即XP关于扩张。

设 ${M_{i}}_{i \in I}$ 是一簇X-投射模，任意R-模 $N \in X$ ，由同构式 ${Ext}_{R}^{1} (\oplus_{i \in I} M_{i}, N) ≅ \prod_{i \in I} {Ext}_{R}^{1} (M_{i}, N)$ 可得XP关于直和项封闭。

于是，结合引理3.9，下面我们弱化命题3.8。

命题3.10 设R是左wGXP封闭环， $0 \to N \to M \to X \to 0$ 是R-模的正合列，其中 $X \in X P$ ，则 $M \in w G X P$ $\Leftrightarrow$ $N \in w G X P$ 。

证明 ( $\Rightarrow$ )设 $M \in w G X P$ ，则由命题3.4可知存在正合列 $0 \to M \to P \to K \to 0$ ，其中 $P \in X P$ ， $K \in w G X P$ 。考虑推出图

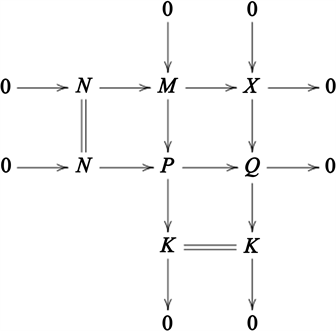
因为 $X \in X P \subseteq w G X P$ ， $K \in w G X P$ ，所以 $Q \in w G X P$ ，则对中间行用命题3.4可得 $N \in w G X P$ 。

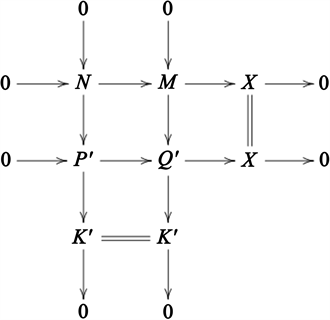
( $\Leftarrow$ )设 $N \in w G X P$ ，则由命题3.4可知存在正合列 $0 \to N \to P^{'} \to K^{'} \to 0$ ，其中 $P^{'} \in X P$ ， $K^{'} \in w G X P$ 。考虑推出图

因为 $P^{'}, X \in X P$ ，所以由引理3.9可知 $Q^{'} \in X P$ ，则对中间列用命题3.4可得 $M \in w G X P$ 。

命题3.11 设R是环，M是一R-模，则以下等价：

1) 若 $M \in R - M o d$ ，则 $M \in w G X P$ ；

2) 若 $M \in w G I$ ，则 $M \in w G X P$ ；

3) 若 $M \in G I$ ，则 $M \in w G X P$ ；

4) 若 $M \in S G I$ ，则 $M \in w G X P$ ；

5) 若 $M \in I$ ，则 $M \in w G X P$ ；

6) 若 $M \in I$ ，则 $M \in X P$ 。

证明 (1) $\Rightarrow$ (2) $\Rightarrow$ (3) $\Rightarrow$ (4) $\Rightarrow$ (5)，(6) $\Rightarrow$ (5)显然。

(5) $\Rightarrow$ (6)设 $M \in I$ ，则由条件可知 $M \in w G X P$ 。于是由命题3.4可知存在正合列 $0 \to M \to P \to N \to 0$ ，其中 $P \in X P$ , $N \in w G X P$ 。因为 $M \in I$ ，所以正合列 $0 \to M \to P \to N \to 0$ 可裂，因此由引理3.9可知 $M \in X P$ 。

(6) $\Rightarrow$ (1) $M \in R - M o d$ ，取M的投射分解和内射分解相连接，则存在正合列

$\dots \to P_{1} \to P_{0} \to E_{0} \to E_{1} \to \dots$

其中 $P_{i} \in P \subseteq X P$ ， $E_{i} \in I \subseteq X P (i \in ℕ)$ ，故 $M \in w G X P$ 。

推论3.12 设R是环，M是一R-模，考虑下面R-模的正合列

$0 \to G_{n} \to G_{n - 1} \to \dots \to G_{0} \to M \to 0$

和

$0 \to H_{n} \to H_{n - 1} \to \dots \to H_{0} \to M \to 0$ ,

其中 $G_{0}, \dots, G_{n - 1}, H_{0}, \dots, H_{n - 1} \in w G X P$ 。若wGXP关于扩张封闭，则 $G_{n} \in w G X P$ 当且仅当 $H_{n} \in w G X P$ 。

证明类似于文献( [10]，引理2.1)的证明。

4. X-投(内)射维数

本部分我们引入模M的X-投(内)射维数，讨论在任意环上GXP(GXI)、wGXP(wGXI)、GP(GI)和wGP(wGI)四者之间的联系。

定义4.1 设R是环，M是一R-模，我们如下定义模M的X-投射维数：

$X - p d (M) = i n f {n \in ℕ |$ 存在正合列 $0 \to X_{n} \to X_{n - 1} \to \dots \to X_{0} \to M \to 0$ ，其中 $X_{i} \in X P$ ， $i = 0, 1, \dots, n}$ 。

若上述集合为空集，则规定 $X - p d (M) = \infty$ 。

如下定义模M的X-内射维数：

$X - i d (M) = i n f {n \in ℕ |$ 存在正合列 $0 \to M \to X_{0} \to \dots \to X_{n - 1} \to X_{n} \to 0$ ，其中 $X_{i} \in X I$ ， $i = 0, 1, \dots, n}$ 。

若上述集合为空集，则规定 $X - i d (M) = \infty$ 。

下面我们讨论模M的X-投射维数的相关结论，关于模M的X-内射维数，均有对偶结论。

命题4.2 设R是环， $l D (R) < \infty$ ，M是一R-模，若 $X - p d (M) \leq 1$ ，则以下等价：

1) $M \in w G P$ ；

2) $M \in w G X P$ ；

3) $M \in G P$ ；

4) $M \in G X P$ ；

证明由文献( [5]，命题2.1.1)可知(1) $\Leftrightarrow$ (2)，(3) $\Leftrightarrow$ (4)。

(3) $\Rightarrow$ (1)显然。

(1) $\Rightarrow$ (3)设 $M \in w G P$ ，则存在投射模的正合列 $Ψ = \dots \to P_{1} \to P_{0} \to P^{0} \to P^{1} \to \dots$ ，使得 $M ≅ Ker (P^{0} \to P^{1})$ 。只需证对任意投射模Q，序列 $H o m_{R} (Ψ, Q)$ 正合即可。设 $i d (Q) = n < \infty$ ，我们对n进行数学归纳。当 $n = 0$ 时，序列 $H o m_{R} (Ψ, Q)$ 显然正合。设 $n \geq 1$ ，则对模Q存在正合列 $0 \to Q \to E \to L \to 0$ ，其中 $E \in I$ , $i d (L) = n - 1$ 。因此存在正合列 $0 \to H o m_{R} (Ψ, Q) \to H o m_{R} (Ψ, E) \to H o m_{R} (Ψ, L) \to 0$ 。由归纳假设可得，序列 $H o m_{R} (Ψ, L)$ 正合。显然序列 $H o m_{R} (Ψ, E)$ 也正合，故序列 $H o m_{R} (Ψ, Q)$ 正合。

推论4.3 设R是环，若 $l D (R) \leq 1$ ，则模类GP、GXP、wGP和wGXP是同一个类。

文章引用

武新文. 弱Gorenstein X-投(内)射模
Weak Gorenstein X-Projective (Injective) Modules[J]. 理论数学, 2022, 12(04): 525-531. https://doi.org/10.12677/PM.2022.124058

参考文献

1. Fay, T. and Joubert, S. (1994) Relatively Injectivity. Chinese Journal of Mathematics, 22, 65-94.

2. Enochs, E.E. and Jenda, O.M.G. (1995) Gorenstein Injective and Projective Modules. MathZ, 220, 611-633. https://doi.org/10.1007/BF02572634

3. Bennis, D. and Mahdou, N. (2007) Strongly Gorenstein Projective, In-jective, and Flat Modules. Journal of Pure and Applied Algebra, 210, 437-445. https://doi.org/10.1016/j.jpaa.2006.10.010

4. Gao, Z.H. (2013) Weak Gorenstein Projective, Injective and Flat Modules. Journal of Algebra and Its Applications, 12, 3841-3858. https://doi.org/10.1080/00927872.2011.597809

5. Umamaheswaran, A. and Selvaraj, C. (2014) A Study on X-Injective and Gorenstein X-Injective Modules. India Periyar University, Tamil Nadu.

6. 陈文静, 杨晓燕. 弱Gorenstein FP-内射模[J]. 四川师范大学学报(自然科学版), 2014, 37(4): 477-481.

7. 陈文静, 杨晓燕. 强和强泛Gorenstein FP-内射模[J]. 西南大学学报(自然科学版), 2014, 36(8): 75-78.

8. 袁倩, 张文汇. 强泛Gorenstein FC-投射模[J]. 理论数学, 2021, 11(4): 647-653.https://doi.org/10.12677/pm.2021.114078

9. Holm, H. (2004) Gorenstein Homological Dimensions. Journal of Pure and Applied Algebra, 189, 167-193. https://doi.org/10.1016/j.jpaa.2003.11.007

10. Zhu, X.S. (2013) Resolving Resolution Dimensions. Algebras and Representation Theory, 16, 1165-1191. https://doi.org/10.1007/s10468-012-9351-5

期刊菜单