Modern Physics
Vol.4 No.05(2014), Article ID:14132,23 pages
DOI:10.12677/MP.2014.45015
The Hypothesis of Microcosmic Particle Visualize Model
The Management Bureau of Luanhe River Water Resource under HWCC, Qianxi
Email: Tqj1960@163.com
Copyright © 2014 by author and Hans Publishers Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/



Received: Jul. 18th, 2014; revised: Aug. 1st, 2014; accepted: Aug. 12th, 2014
ABSTRACT
The micro-particle wave-particle duality would be easy to understand through the
new conception of microscopic particles double-wave packet double-origin (two-string
dual-origin) model. The concept of w-p space and s-t space were proposed, then concepts
of full-time
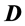 and all-momentum
and all-momentum
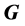 were defined and the relationship between them was illustrated. A new equation of
microscopic particles motion was established. Based on a new particle model, the
classical concepts’ physical meanings of the spin, electrons, protons, neutrons,
interaction force of antiparticles and micro-particle were discussed. Then the structure
and motion of the simplest hydrogen atoms were qualitatively described.
were defined and the relationship between them was illustrated. A new equation of
microscopic particles motion was established. Based on a new particle model, the
classical concepts’ physical meanings of the spin, electrons, protons, neutrons,
interaction force of antiparticles and micro-particle were discussed. Then the structure
and motion of the simplest hydrogen atoms were qualitatively described.
Keywords:The double-Wave Packet Double-Origin Model, Full-Time , All-Momentum
, All-Momentum , Particles in
the New Equation, Gravity
, Particles in
the New Equation, Gravity

微观粒子形象模型假说
田清聚
水利部海委引滦工程管理局,迁西
Email: Tqj1960@163.com
收稿日期:2014年7月18日;修回日期:2014年8月1日;录用日期:2014年8月12日

摘 要
提出微观粒子双波包双原点(双弦双原点)模型,新模型使微观粒子波–粒二象性不再费解。提出w-p空间和s-t空间概念,在此基础上定义了全时间 和全动量
和全动量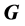 并明确了它们之间的关系。建立微观粒子运动新方程。以粒子新模型为基础对诸如自旋、电子、质子、中子、反粒子和微观粒子相互作用力等经典概念的物理内涵进行了讨论。进而对自然界最简单的宏观粒子氢原子的结构和运动作了定性描述。
并明确了它们之间的关系。建立微观粒子运动新方程。以粒子新模型为基础对诸如自旋、电子、质子、中子、反粒子和微观粒子相互作用力等经典概念的物理内涵进行了讨论。进而对自然界最简单的宏观粒子氢原子的结构和运动作了定性描述。
关键词
双波包双原点模型,全时间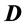 ,全动量
,全动量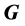 ,粒子运动新方程,引力
,粒子运动新方程,引力

1. 引言
量子力学基本观点[1] 简述如下:
(1) 德布罗意波存在且关系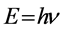 ,
,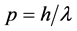 ,成立。微观自由粒子与能量
,成立。微观自由粒子与能量 、动量
、动量 都有确定值的状态波函数平面波相联系。
都有确定值的状态波函数平面波相联系。
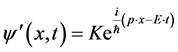 (1)
(1)
(2) 自然界任一真实存在的微观粒子状态波函数 可以看成不同动量的平面波组的迭加,且如下傅立叶变换关系式成立。
可以看成不同动量的平面波组的迭加,且如下傅立叶变换关系式成立。
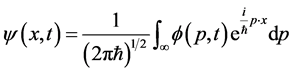 (2)
(2)
 (3)
(3)
(3) 和粒子相联系的波是几率波。波函数在空间中某一点的强度(振幅绝对值的平方)和在该点测量到粒子能量子的几率成比例。
分析以上基本观点可以推论:任一真实存在的微观粒子非相互作用一般状态在人们熟悉的 时空中形象为一波函数
时空中形象为一波函数 波包。而由于微观自由粒子平面波
波包。而由于微观自由粒子平面波 参数
参数 和
和 、
、 和
和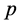 分别存在非常严格的对称关系的启示,所以大胆认为非定态微观粒子动量
分别存在非常严格的对称关系的启示,所以大胆认为非定态微观粒子动量 、能量
、能量 的值和参数
的值和参数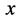 、
、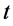 一样也存在有一取值范围,其形象同样可想象成一波包记作
一样也存在有一取值范围,其形象同样可想象成一波包记作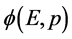 。两个波包是同一微观粒子分别在两个“空间”的两面。因此断定自然界应该还存在着人类没能直观感知的能量、动量“空间”。本文认为:全面研究在两个“空间”中互为因果的两个波包的运动,并在此基础上寻求建立新的物理概念,就能够进一步揭示微观粒子波—粒二象性质,从而建立起物理上更通俗易懂的微观粒子新“形象”。
。两个波包是同一微观粒子分别在两个“空间”的两面。因此断定自然界应该还存在着人类没能直观感知的能量、动量“空间”。本文认为:全面研究在两个“空间”中互为因果的两个波包的运动,并在此基础上寻求建立新的物理概念,就能够进一步揭示微观粒子波—粒二象性质,从而建立起物理上更通俗易懂的微观粒子新“形象”。
2. 两个空间的猜想
2.1. 经典物理学中的三维矢量空间
直觉和经验告诉人们人类可直接感触并赖以生存的自然界是三维 位形世界。假如,某观察者
位形世界。假如,某观察者 在一特定时刻想知道自己和远处某一静止物体
在一特定时刻想知道自己和远处某一静止物体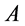 的距离
的距离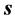 ,可以以
,可以以 为原点建立三维迪卡坐标参考系
为原点建立三维迪卡坐标参考系
如图1所示。则距离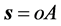 就能用物体
就能用物体 在迪卡坐标参考系中的三个坐标求得:
在迪卡坐标参考系中的三个坐标求得:

Figure 1. Three dimensional
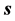 vector space
vector space
图1. 三维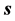 矢量空间
矢量空间
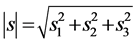 (4)
(4)
若考虑物体 的方位,距离
的方位,距离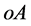 可表示成矢量
可表示成矢量
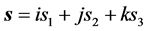 (5)
(5)
2.2. 四维s-t空间的提出
实际上,若图1中物体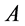 静止也就是说它的速度为零时,其静止能量
静止也就是说它的速度为零时,其静止能量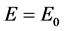 ,距离
,距离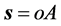 为纯空间距离
为纯空间距离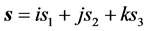 ;假若图1中物体
;假若图1中物体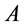 的速度不为零,那么,由狭义相对论知道其能量满足
的速度不为零,那么,由狭义相对论知道其能量满足 ,
, 为物体
为物体 静止能量
静止能量 和动量
和动量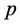 的共同贡献。现在要问,该情况其距离
的共同贡献。现在要问,该情况其距离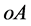 是否依然为
是否依然为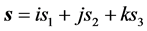 没有变化呢?本文认为:距离
没有变化呢?本文认为:距离 的结构和意义与物体
的结构和意义与物体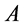 的运动状态密切相关,比照能量表达式该情况
的运动状态密切相关,比照能量表达式该情况 可表示为
可表示为
 (6)
(6)
对式6的意义理解如下: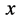 为观察点
为观察点 与物体
与物体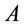 所在点的时空距离。
所在点的时空距离。 为观察点
为观察点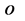 相对与物体
相对与物体 所在点所具有的相对时间,也可以理解为物体
所在点所具有的相对时间,也可以理解为物体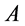 所在点的钟表比观察点
所在点的钟表比观察点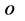 点的钟表慢或快
点的钟表慢或快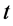 时间,
时间, 为不含时间的纯空间距离意义不变。例如,(1)
当物体
为不含时间的纯空间距离意义不变。例如,(1)
当物体 速度为零静止情况,物体
速度为零静止情况,物体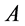 所在点钟表和观察点
所在点钟表和观察点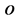 计时钟表走的一样快,读数相同时间差
计时钟表走的一样快,读数相同时间差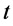 为零,距离
为零,距离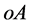 可表示为
可表示为 ;(2) 当极端状态物体
;(2) 当极端状态物体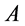 为光子速度为常数
为光子速度为常数 情况出现时,光子
情况出现时,光子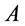 所在点钟表停滞时间不流逝读数恒为零,因此,和光子绑定的钟表与观察点
所在点钟表停滞时间不流逝读数恒为零,因此,和光子绑定的钟表与观察点 静止时钟时间差是全部时间
静止时钟时间差是全部时间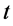 ,由狭义相对论知道该情况其距离
,由狭义相对论知道该情况其距离 可表示为
可表示为 ;(3)
一般情况物质粒子
;(3)
一般情况物质粒子 速度
速度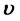 界于0与光速常数
界于0与光速常数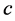 之间,它的四个主要参数之间存在如下关系
之间,它的四个主要参数之间存在如下关系
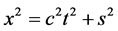
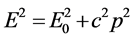
综上所述特提出四维s-t空间定义:自然界存在四维s-t空间,该空间由三维相互垂直的虚轴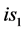 、
、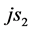 、
、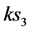 和一维实轴
和一维实轴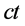 构成,如图2所示。显然,当其实轴
构成,如图2所示。显然,当其实轴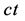 相对时间
相对时间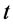 为零时,四维s-t空间就变为了图1所表示的三维
为零时,四维s-t空间就变为了图1所表示的三维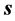 空间。值得注意的是这里提出的四维s-t空间有着全新的物理意义。它同狭义相对论中悯可夫斯基x-t四维空间[2]
有区别,后者是由三维
空间。值得注意的是这里提出的四维s-t空间有着全新的物理意义。它同狭义相对论中悯可夫斯基x-t四维空间[2]
有区别,后者是由三维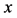 空间加上虚时间维
空间加上虚时间维 组成。而s-t四维空间中的时间维
组成。而s-t四维空间中的时间维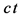 是实数轴。简要表述就是:四维s-t空间中的任一点
是实数轴。简要表述就是:四维s-t空间中的任一点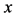 的值可用四个坐标来表示,也可以说
的值可用四个坐标来表示,也可以说 为一哈密
为一哈密
顿“四元数”。并且关系式成立。
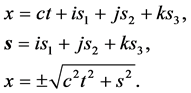 (7)
(7)
式中,参数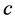 为光速常数,参数
为光速常数,参数 为相对时间。
为相对时间。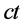 为“四元数”
为“四元数”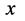 的实部;
的实部; 的虚部
的虚部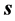 可以理解为相对时间
可以理解为相对时间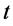 为零时静止粒子的位置参数
为零时静止粒子的位置参数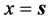 。可见,人们熟悉的三维
。可见,人们熟悉的三维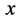 空间中任意方向矢量都是四维s-t空间
空间中任意方向矢量都是四维s-t空间 和与之正交的矢量
和与之正交的矢量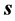 两维的矢量和,因此,它与狭义相对论原理不矛盾。
两维的矢量和,因此,它与狭义相对论原理不矛盾。
2.3. 四维w-p空间概念
大量的物理现象隐约揭示自然界还存在一个四维w-p空间。该空间如下定义:w-p空间是四维空间如图3所示,它由一维实轴 和三维相互垂直的虚轴
和三维相互垂直的虚轴 构成,当确定了坐标原点后,四维w-p空间中的任一点
构成,当确定了坐标原点后,四维w-p空间中的任一点 可以表示为一哈密顿“四元数”。并且关系式成立。
可以表示为一哈密顿“四元数”。并且关系式成立。
 (8)
(8)
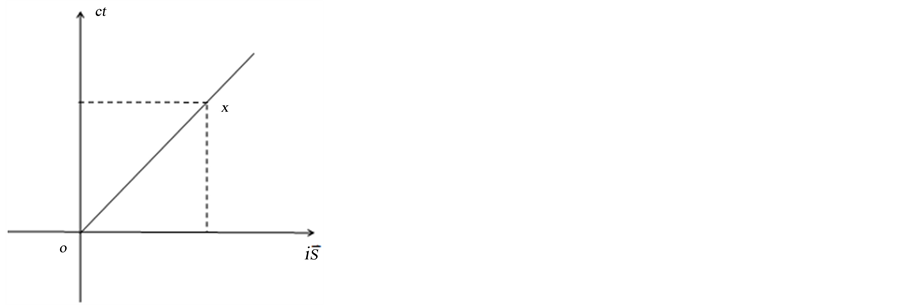
Figure 2. Schematic diagram of four dimensional s-t space
图2. 四维s-t空间示意图

Figure 3. Schematic diagram of four dimensional w-p space
图3. 四维w-p空间示意图
式中,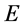 和
和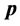 分别代表粒子的能量参数和动量参数,
分别代表粒子的能量参数和动量参数,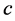 为光速常数,而参数
为光速常数,而参数 的意义可以理解为当动量
的意义可以理解为当动量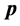 为零时静止粒子的能量,也就是我们通常所说的
为零时静止粒子的能量,也就是我们通常所说的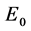 。诚然,截止目前由于人类自然形态的特殊性我们对四维w-p空间研究甚少,实际上,经典物理学和迄今为止的人类宏观活动的确没有显现必须四维w-p空间参与的必然要求,可是自从人类实践的触角进入到微观物质世界以后,对四维w-p空间的探索或许就是必须的了。否则,很多自然现象将不易被我们认识和了解。微观物质世界本质的许多方面就不易简单直观地被揭示。
。诚然,截止目前由于人类自然形态的特殊性我们对四维w-p空间研究甚少,实际上,经典物理学和迄今为止的人类宏观活动的确没有显现必须四维w-p空间参与的必然要求,可是自从人类实践的触角进入到微观物质世界以后,对四维w-p空间的探索或许就是必须的了。否则,很多自然现象将不易被我们认识和了解。微观物质世界本质的许多方面就不易简单直观地被揭示。
2.4. 三维 空间与四维s-t空间关系
空间与四维s-t空间关系
受客观实在局限人类仅仅能够在三维 空间直接感知自然界。那么现在要问三维
空间直接感知自然界。那么现在要问三维 位形空间与上文提出的四维s-t空间和四维w-p空间到底存在着怎样的关系呢?
位形空间与上文提出的四维s-t空间和四维w-p空间到底存在着怎样的关系呢?
可以这样想象:建立了迪卡儿坐标系的三维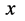 空间世界里任一
空间世界里任一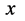 点在没有物质粒子在该点出现时其与迪卡儿坐标系原点
点在没有物质粒子在该点出现时其与迪卡儿坐标系原点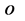 连线
连线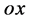 的值可表示为
的值可表示为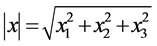 ,如若四维s-t空间存在那么
,如若四维s-t空间存在那么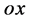 也应能表示为其中某方向直线上的线段,但由于四维s-t空间坐标系方位与可能出现在
也应能表示为其中某方向直线上的线段,但由于四维s-t空间坐标系方位与可能出现在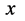 点的被观测粒子运动状态相关联,所以说没有物质粒子在
点的被观测粒子运动状态相关联,所以说没有物质粒子在 点出现的
点出现的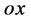 状态结构在四维s-t空间的意义不确定。如下的形容可能接近客观事实,三维
状态结构在四维s-t空间的意义不确定。如下的形容可能接近客观事实,三维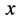 迪卡儿坐标系中粒子波函数
迪卡儿坐标系中粒子波函数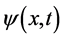 与一系列以速度
与一系列以速度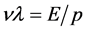 传播着但原点不确定的四维s-t空间坐标系相关联。假若(1)
三维迪卡坐标系原点静止时钟0时刻在三维
传播着但原点不确定的四维s-t空间坐标系相关联。假若(1)
三维迪卡坐标系原点静止时钟0时刻在三维 空间
空间 点出现一光粒子,我们认为随着光粒子的出现与其相关联的四维s-t空间迪卡儿坐标系原点与三维
点出现一光粒子,我们认为随着光粒子的出现与其相关联的四维s-t空间迪卡儿坐标系原点与三维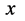 空间坐标系中的
空间坐标系中的 点重合。由于光粒子四维迪卡儿坐标系的实轴
点重合。由于光粒子四维迪卡儿坐标系的实轴 总是与三维
总是与三维 空间坐标系
空间坐标系 重合,所以相对于三维迪卡坐标系原点静止时钟来说,与光粒子(四维s-t空间坐标系原点)绑定的时钟读数一定为
重合,所以相对于三维迪卡坐标系原点静止时钟来说,与光粒子(四维s-t空间坐标系原点)绑定的时钟读数一定为 ,因此
,因此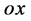 具有了确切意义
具有了确切意义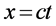 ,光粒子能量
,光粒子能量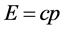 ;(2)
因为出现的静止粒子四维迪卡儿坐标系的某一虚矢量
;(2)
因为出现的静止粒子四维迪卡儿坐标系的某一虚矢量 总是与三维
总是与三维 空间坐标系
空间坐标系 重合,所以当静止粒子在
重合,所以当静止粒子在 点出现时,三维
点出现时,三维 迪卡坐标系中依然还是
迪卡坐标系中依然还是 但静止粒子相关联四维s-t空间与光粒子出现时相比较其方位旋转了九十度角。
但静止粒子相关联四维s-t空间与光粒子出现时相比较其方位旋转了九十度角。 确切意义
确切意义 ,粒子能量
,粒子能量 。因此可以说:三维
。因此可以说:三维 空间某确定点
空间某确定点 出现被观测粒子瞬间,与其关联的四维s-t空间原点总是与被观测粒子出现点
出现被观测粒子瞬间,与其关联的四维s-t空间原点总是与被观测粒子出现点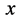 相重合,与此同时三维
相重合,与此同时三维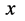 坐标系原点与被观测粒子另一关联四维w-p空间原点重合,观测者在该重合点看,被观测粒子四维w-p空间能量
坐标系原点与被观测粒子另一关联四维w-p空间原点重合,观测者在该重合点看,被观测粒子四维w-p空间能量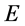 方向与三维
方向与三维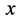 空间
空间 方向平行时,三维
方向平行时,三维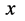 空间存在光波出现光粒子,被观测粒子能量
空间存在光波出现光粒子,被观测粒子能量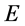 能被完全观测到;能量
能被完全观测到;能量 方向与
方向与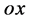 方向垂直时,三维
方向垂直时,三维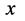 空间存在波前传播速率为无穷大的物质波静止粒子出现。
空间存在波前传播速率为无穷大的物质波静止粒子出现。
3. 双波包双原点(双弦双原点)粒子模型
为了建立微观粒子直观的物理形象,进一步揭示波--粒二象性的实质特提出如下假说:
(1) 三维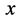 空间任一微观粒子都是与其相关联的四维s-t空间和能量四维w-p空间相互作用的一特定表象。德布罗意波存在且与微观粒子相联系,微观粒子非相互作用状态在人类赖以生存的三维
空间任一微观粒子都是与其相关联的四维s-t空间和能量四维w-p空间相互作用的一特定表象。德布罗意波存在且与微观粒子相联系,微观粒子非相互作用状态在人类赖以生存的三维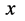 空间可以用一状态波函数
空间可以用一状态波函数 来表征;在三维能量
来表征;在三维能量 空间也可以用一状态波函数
空间也可以用一状态波函数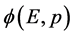 来表征。两个波函数
来表征。两个波函数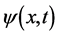 和
和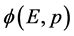 是同一粒子的两面。在波函数
是同一粒子的两面。在波函数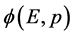 定义域中的每一对确定数
定义域中的每一对确定数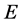 、
、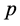 ,都对应真实存在的三维
,都对应真实存在的三维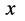 空间中一平面波
空间中一平面波
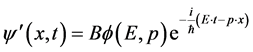 (9)
(9)
在波函数 定义域中的每一对确定数
定义域中的每一对确定数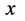 、
、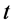 ,也都对应三维
,也都对应三维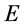 空间中一“平面”波
空间中一“平面”波
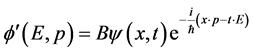 (10)
(10)
而波函数 和
和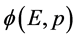 分别是两空间中平面波组的迭加。当
分别是两空间中平面波组的迭加。当 为常数条件满足时,傅立叶变换式成立。
为常数条件满足时,傅立叶变换式成立。

当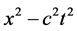 为常数时傅立叶变换式成立。
为常数时傅立叶变换式成立。

(2) 在三维 空间粒子波函数
空间粒子波函数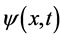 中某一点的强度(振幅绝对值的平方)和在该点找到粒子“作用点”
中某一点的强度(振幅绝对值的平方)和在该点找到粒子“作用点” (与其关联的四维s-t空间原点)的几率成比例;在能量
(与其关联的四维s-t空间原点)的几率成比例;在能量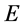 空间粒子另一波函数
空间粒子另一波函数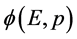 中某一点的强度和在该点找到粒子“作用点”
中某一点的强度和在该点找到粒子“作用点”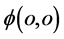 (与其关联的四维w-p空间原点)的几率成比例。进一步指出:三维
(与其关联的四维w-p空间原点)的几率成比例。进一步指出:三维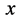 空间波函数
空间波函数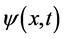 中粒子“作用点”
中粒子“作用点”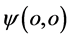 就是具有了能量、动量的粒子能量子出现点,也就是该粒子参与相互作用交换能量
就是具有了能量、动量的粒子能量子出现点,也就是该粒子参与相互作用交换能量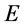 的点。同理,能量
的点。同理,能量 空间波函数
空间波函数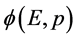 中粒子“作用点”
中粒子“作用点” 出现点就是该粒子参与相互作用交换
出现点就是该粒子参与相互作用交换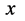 的点,因此,微观粒子有“双波包双原点形象”。显然,微观粒子波函数
的点,因此,微观粒子有“双波包双原点形象”。显然,微观粒子波函数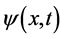 振幅不为零的定义域中哪一点能成为粒子出现点原点
振幅不为零的定义域中哪一点能成为粒子出现点原点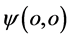 ;波函数
;波函数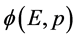 定义域中哪一点能成为粒子出现点原点
定义域中哪一点能成为粒子出现点原点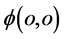 须由振幅强度比例随机确定。(3)
微观粒子相互作用瞬时(微观粒子出现瞬时),各参与相互作用微观粒子的波函数
须由振幅强度比例随机确定。(3)
微观粒子相互作用瞬时(微观粒子出现瞬时),各参与相互作用微观粒子的波函数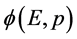 原点
原点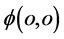 同步确定(波包塌缩)且在三维
同步确定(波包塌缩)且在三维 空间碰撞重合出现在三维
空间碰撞重合出现在三维 空间某一定点。该点就是该相互作用事件伴生的“宏观”粒子(例如原子)在三维
空间某一定点。该点就是该相互作用事件伴生的“宏观”粒子(例如原子)在三维 空间的原心。一般地,人们习惯指定这样的点作为三维
空间的原心。一般地,人们习惯指定这样的点作为三维 坐标参考系的原点。另一方面,相互作用各参与粒子波函数
坐标参考系的原点。另一方面,相互作用各参与粒子波函数 同步“塌缩”在各自定义域内点
同步“塌缩”在各自定义域内点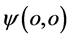 ,各参与粒子能量子分别同步出现。所有参与粒子的点
,各参与粒子能量子分别同步出现。所有参与粒子的点 在能量
在能量 空间碰撞重合出现在能量
空间碰撞重合出现在能量 空间某一确定“作用点”彼此交换能量。
空间某一确定“作用点”彼此交换能量。 们在能量
们在能量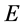 空间出现点是“宏观”粒子原子的另一个原心。仔细分析可知,两个原心点
空间出现点是“宏观”粒子原子的另一个原心。仔细分析可知,两个原心点 和
和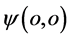 之间的连接直线具有双重意义,其一是微观粒子s-t空间结构中的
之间的连接直线具有双重意义,其一是微观粒子s-t空间结构中的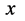 (三维
(三维 空间
空间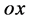 );其二是微观粒子w-p空间结构中的能量
);其二是微观粒子w-p空间结构中的能量 。因此,我们说相互作用过程中微观粒子有“双弦双原点”形象。
。因此,我们说相互作用过程中微观粒子有“双弦双原点”形象。
可以想象一个图景:沿同一直线相反方向运动的两个高能光子相撞,撞击瞬间点 和
和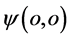 重合又分开有可能产生正、负电子对,电子对在三维
重合又分开有可能产生正、负电子对,电子对在三维 空间有共同
空间有共同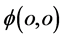 点、在三维
点、在三维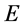 空间有共同
空间有共同 点能够电磁相互作用而烟没再变为两光子。那么我们的问题是,沿垂直方向运动的两个能量足够大的光子相撞,若也产生带正、负电荷的两个实物粒子的话,合理的推断该情况应该产生在双空间有大对称性质的质子和电子组合–氢原子。
点能够电磁相互作用而烟没再变为两光子。那么我们的问题是,沿垂直方向运动的两个能量足够大的光子相撞,若也产生带正、负电荷的两个实物粒子的话,合理的推断该情况应该产生在双空间有大对称性质的质子和电子组合–氢原子。
举例说明在三维 空间观察相互作用瞬间单个微观粒子
空间观察相互作用瞬间单个微观粒子 ,如图4所示,若观察者站在“作用点”三维坐标系原点
,如图4所示,若观察者站在“作用点”三维坐标系原点 处,他将看到什么呢?可以想象,观察者能够如下描述粒子
处,他将看到什么呢?可以想象,观察者能够如下描述粒子 :在距离坐标原点
:在距离坐标原点 为
为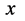 的地方粒子
的地方粒子 波函数
波函数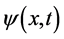 “塌缩”在振幅极值点
“塌缩”在振幅极值点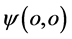 ,与此同时
,与此同时 点与w-p空间相交具有了粒子性能量
点与w-p空间相交具有了粒子性能量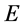 和动量
和动量 。如果,粒子
。如果,粒子 的能量
的能量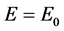 相对时间
相对时间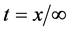 为零,则
为零,则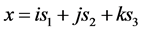 粒子
粒子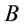 是静止粒子;如果,粒子
是静止粒子;如果,粒子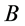 的能量
的能量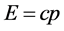 、时间
、时间 ,则
,则 粒子
粒子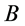 就是光粒子。显然,能量
就是光粒子。显然,能量 和动量
和动量 确定后,粒子
确定后,粒子 在三维
在三维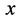 空间正处在一几率波定态,具有确定频率
空间正处在一几率波定态,具有确定频率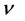 和波长
和波长 。因此,观察者能计算得出粒子
。因此,观察者能计算得出粒子 的相对时间参数
的相对时间参数 。该时间参数
。该时间参数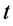 和能量
和能量 、动量
、动量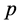 位置参数
位置参数 一样是微观粒子
一样是微观粒子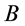 在该定态的特征参数。一般地,波包塌缩瞬间观测者粒子和被观测粒子相互作用各自参数发生变化。对于每一单个粒子而言,每一次参与相互作用它的两个波函数的两个相交点都将变化其表现为该物质粒子的质量
在该定态的特征参数。一般地,波包塌缩瞬间观测者粒子和被观测粒子相互作用各自参数发生变化。对于每一单个粒子而言,每一次参与相互作用它的两个波函数的两个相交点都将变化其表现为该物质粒子的质量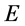 、动量
、动量 、位置
、位置 和参数
和参数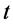 的不断变化,从而两个波函数也同步改变。可观测参数的变化反映的是微观物质粒子性的一面,而两个波函数的变化反映微观物质波动性的一面。
的不断变化,从而两个波函数也同步改变。可观测参数的变化反映的是微观物质粒子性的一面,而两个波函数的变化反映微观物质波动性的一面。
微观物质粒子两个波函数 和
和 中每一个振幅不为零的点都是两空间s-t空间和w-p空间
中每一个振幅不为零的点都是两空间s-t空间和w-p空间
可能的相交点。上节图示了三维 空间中微观物质粒子被观察测量事件。现在考虑假若在能量
空间中微观物质粒子被观察测量事件。现在考虑假若在能量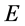 空间中研究同一事件见图5将是一种什么图景呢。可以想象,在三维能量
空间中研究同一事件见图5将是一种什么图景呢。可以想象,在三维能量 空间中,若观察者站在“作用点”即坐标参考系原点
空间中,若观察者站在“作用点”即坐标参考系原点 处研究相互作用状态的粒子
处研究相互作用状态的粒子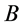 ,一定能看到如下信息:在距离坐标原点
,一定能看到如下信息:在距离坐标原点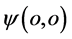 为
为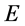 的地方粒子
的地方粒子 波函数
波函数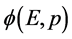 “塌缩”在振幅极值点
“塌缩”在振幅极值点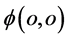 且该振幅极值点与s-t空间相交具有了粒子性参数
且该振幅极值点与s-t空间相交具有了粒子性参数 和相对时间
和相对时间 。同理,参数
。同理,参数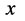 和时间
和时间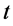 确定以后,该粒子
确定以后,该粒子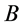 在三维能量
在三维能量 空间显现点粒子性质且其处在一“几率波”定态,具有确定频率和波长。所以观测者将能记下微观粒子
空间显现点粒子性质且其处在一“几率波”定态,具有确定频率和波长。所以观测者将能记下微观粒子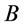 确定参数值能量
确定参数值能量 、动量
、动量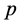 。
。
4. 拓展时间和动量概念
至此,本文对单个微观粒子结构的讨论引进了微观粒子“四元数”距离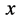 概念和“四元数”能量
概念和“四元数”能量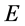 概念,而传统的时间
概念,而传统的时间 和动量
和动量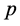 没有改变。然而,如果微观物质是双“四维”构造,我们有理由认为描述微观粒子的四个基本参数能量
没有改变。然而,如果微观物质是双“四维”构造,我们有理由认为描述微观粒子的四个基本参数能量 、距离
、距离 、时间
、时间 和动量
和动量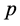 都有“四元数”结构,因此提出“全时间
都有“四元数”结构,因此提出“全时间 ”
”
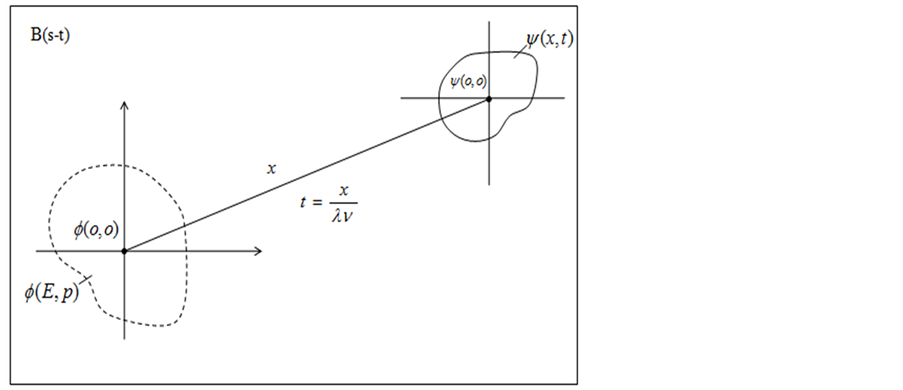
Figure 4. s-t Space micro particles appear point wave packet collapse figure
图4. s-t空间微观粒子出现点波包塌缩示意图
Figure 5. w-p Space micro particles appear point wave packet collapse figure
图5. w-p 空间微观粒子出现点波包塌缩示意图
和“全动量 ”新概念。
”新概念。
4.1. 四元数全时间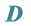 的意义
的意义
全时间D的定义:微观粒子四元数距离x被光速常数c整除等于全时间D。它的四元数结构由实部标量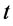 和虚部矢量
和虚部矢量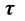 组成,用公式表示如下
组成,用公式表示如下
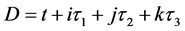 ,(11)
,(11)
可见,全时间D的实部标量 就是通常我们熟悉的相对时间变量,而虚部矢量
就是通常我们熟悉的相对时间变量,而虚部矢量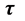 由于其特殊性还不被普遍了解。全时间D和四元数距离
由于其特殊性还不被普遍了解。全时间D和四元数距离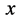 存在如下关系
存在如下关系
 (12)
(12)
比较式7和式12
 ,因此,式7中矢量
,因此,式7中矢量 和上式矢量
和上式矢量 相等。
相等。
4.2. 四元数全动量 的意义
的意义
全动量 的定义:微观粒子四元数能量
的定义:微观粒子四元数能量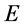 被光速常数
被光速常数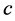 整除等于全动量
整除等于全动量 。它的四元数结构由实部标量
。它的四元数结构由实部标量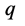 和虚部矢量
和虚部矢量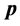 组成,用公式表示如下
组成,用公式表示如下
 (13)
(13)
显然,全动量 的虚部矢量
的虚部矢量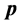 就是人们熟知的可观测量动量,而实部标量
就是人们熟知的可观测量动量,而实部标量 由于其特殊性还不被熟悉。全动量
由于其特殊性还不被熟悉。全动量 和四元数能量
和四元数能量 存在如下关系
存在如下关系
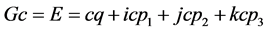 (14)
(14)
同样的,比较式8和式14如下关系成立。
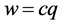
4.3. 全时间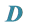 和全动量
和全动量 的关系
的关系
四元数全时间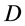 和四元数全动量
和四元数全动量 是本文给出的全新概念,那么它们之间存在什么关系呢?由经典物理学动量
是本文给出的全新概念,那么它们之间存在什么关系呢?由经典物理学动量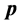 计算公式
计算公式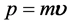 得到启示,大胆推断全时间
得到启示,大胆推断全时间 和全动量
和全动量 各分量关系如下:
各分量关系如下:
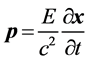 (15)
(15)
 (16)
(16)
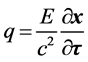 (17)
(17)
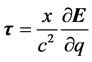 (18)
(18)
分析式15和式18,偏微分 和
和 是矢量,所以,参数
是矢量,所以,参数 和参数
和参数 也为矢量;偏微分
也为矢量;偏微分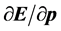 和
和 都是矢量对矢量求导,因此参数
都是矢量对矢量求导,因此参数 和时间
和时间 的方向遵守矢乘法则。而偏微分
的方向遵守矢乘法则。而偏微分 和
和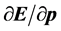 ;
;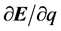 和
和 绝对值相等。
绝对值相等。
4.4. 定态波函数的传播与全速度概念
人类直观感知的自然界是三维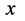 空间世界,若其中任意微观粒子波函数
空间世界,若其中任意微观粒子波函数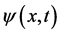 塌缩
塌缩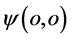 点出现粒子能量子,四参数x、t、E和p有确定值,这时微观粒子定态平面波函数
点出现粒子能量子,四参数x、t、E和p有确定值,这时微观粒子定态平面波函数 的传播方向与粒子能量子出现点x和观察点原点
的传播方向与粒子能量子出现点x和观察点原点 连接直线
连接直线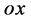 方向相同见图6。直线
方向相同见图6。直线 的意义由该微观粒子四维s-t空间方位所决定。也就是说,如果观察者站在三维x空间迪卡儿坐标系原点即粒子碰撞“作用点”
的意义由该微观粒子四维s-t空间方位所决定。也就是说,如果观察者站在三维x空间迪卡儿坐标系原点即粒子碰撞“作用点”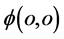 观察该粒子能量子出现点
观察该粒子能量子出现点 能够观测到:(1)
若定态平面波函数
能够观测到:(1)
若定态平面波函数 传播方向
传播方向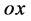 与微观粒子四维s-t空间结构实轴
与微观粒子四维s-t空间结构实轴 方向重合,观测到的一定是光粒子其参数
方向重合,观测到的一定是光粒子其参数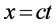 。光平面波
。光平面波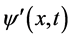 随时间t变化其波前传播速度为光速常数c,全时间
随时间t变化其波前传播速度为光速常数c,全时间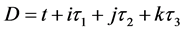 的矢量部分
的矢量部分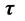 为零。(2)
若定态平面波函数
为零。(2)
若定态平面波函数 传播方向
传播方向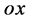 与微观粒子四维s-t空间结构某一虚矢
与微观粒子四维s-t空间结构某一虚矢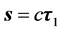 方向相同观测到的肯定是静止粒子
方向相同观测到的肯定是静止粒子 。由于该状态全时间
。由于该状态全时间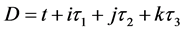 的标量部分相对时间t为零(
的标量部分相对时间t为零( 空间任一点的时钟读数都相同),所以,三维t空间静止粒子平面波函数
空间任一点的时钟读数都相同),所以,三维t空间静止粒子平面波函数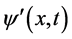 随相对时间t变化,其波前传播速度为
随相对时间t变化,其波前传播速度为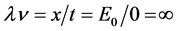 。(3)
一般状态微观粒子三维x空间以t为自变量的定态波函数
。(3)
一般状态微观粒子三维x空间以t为自变量的定态波函数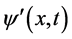 传播方向与其动量
传播方向与其动量 方向相同,也即该粒子能量子出现点x与观察点
方向相同,也即该粒子能量子出现点x与观察点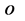 连接直线
连接直线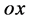 方向。该方向与粒子四维s-t空间直线
方向。该方向与粒子四维s-t空间直线 方向相同。粒子平面波函数
方向相同。粒子平面波函数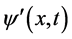 波前传播速度为
波前传播速度为 ,其中
,其中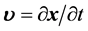 。
。
试想,假如人类不是仅仅能够看到三维x空间世界,而能直接观察四维s-t空间微观粒子的全貌。那么,当参与相互作用波包塌缩粒子出现瞬时,观察者站在碰撞“作用点”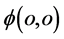 也即迪卡儿坐标系原点应该能够看到距离x对全时间D的全微分
也即迪卡儿坐标系原点应该能够看到距离x对全时间D的全微分 而不仅仅是偏导数
而不仅仅是偏导数 :即有了动量p、能量E的点
:即有了动量p、能量E的点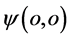 速度为
速度为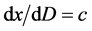 。我们称该速度
。我们称该速度 为微观粒子运动全速度。粒子全速度
为微观粒子运动全速度。粒子全速度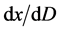 的“模”为光速常量c。且如下公式
的“模”为光速常量c。且如下公式
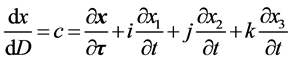 (19)
(19)
成立,若将上式中
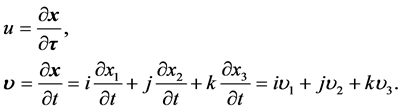
则关系式
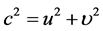 (20)
(20)
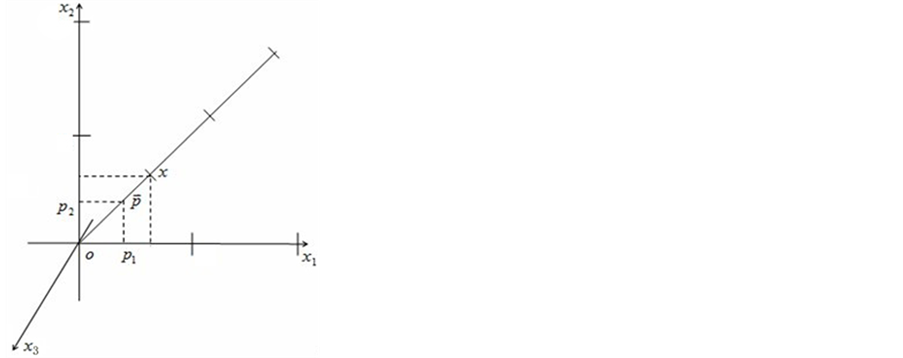
Figure 6. Schematic diagram of De Broglie plan wave propagation
图6. 德布罗意平面波传播示意图
成立。显然,全速度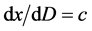 也是“四元数”结构。当粒子为光子时,
也是“四元数”结构。当粒子为光子时,
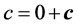
可见,粒子质量m、全动量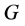 和s-t空间全速度
和s-t空间全速度 的关系为
的关系为 ,不难看出,若承认上面微观粒子全速度概念,那麽微观粒子在s-t空间就不会有绝对静止状态,通常人类在三维x空间观察到的“静止状态”仅是粒子全速度矢量部分
,不难看出,若承认上面微观粒子全速度概念,那麽微观粒子在s-t空间就不会有绝对静止状态,通常人类在三维x空间观察到的“静止状态”仅是粒子全速度矢量部分 为零的状态,那是因为人类生存的局限性不能够觉察到该状态下粒子全速度标量部分
为零的状态,那是因为人类生存的局限性不能够觉察到该状态下粒子全速度标量部分 存在的缘故。为了叙述的方便和前后的一致性本文后面继续将
存在的缘故。为了叙述的方便和前后的一致性本文后面继续将 状态粒子称作“经典静止”粒子。
状态粒子称作“经典静止”粒子。
同理,单个微观粒子在w-p空间的运动全速度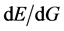 的“模”也为光速常量c,将全速度
的“模”也为光速常量c,将全速度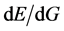 用字母
用字母 表示如下公式成立,
表示如下公式成立,
 (21)
(21)
若将上式中

则关系式
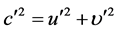 (22)
(22)
存在,可见当粒子在w-p空间速度 常数时,该粒子全速度
常数时,该粒子全速度

同样的,粒子参数 、全时间D和w-p空间全速度
、全时间D和w-p空间全速度 的关系为
的关系为
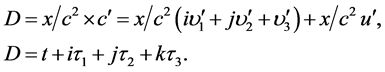
显然,若在s-t空间观察单个微观粒子的运动, 和全时间D参数实部t方向相同,
和全时间D参数实部t方向相同,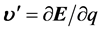 和粒子全时间D参数虚部矢量
和粒子全时间D参数虚部矢量 方向相同。综上所述,对于每一确定粒子如下关系式
方向相同。综上所述,对于每一确定粒子如下关系式
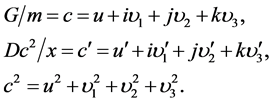 (23)
(23)
成立,不难推断,若s-t空间电子出现点参数 ,x方向和
,x方向和 轴的夹角为
轴的夹角为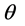 、w-p空间出现点
、w-p空间出现点 ,
, 和
和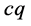 轴的夹角也一定为
轴的夹角也一定为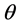 。显然,式23表示微观粒子全速度
。显然,式23表示微观粒子全速度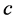 方向的取值范围是一个半径为光速常数
方向的取值范围是一个半径为光速常数 的四维球面。
的四维球面。
5. 对微观粒子波函数的进一步讨论
前文假说中指出,每一个微观粒子非相互作用状态站在三维x空间坐标系原点(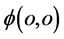 出现点)观察为一几率波函数
出现点)观察为一几率波函数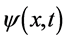 ;在三维E空间坐标系原点(
;在三维E空间坐标系原点(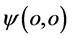 出现点)看表现为另一几率波函数
出现点)看表现为另一几率波函数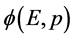 。然而,在提出了全时间D、全动量G概念以后,有必要对单个微观粒子和其几率波函数
。然而,在提出了全时间D、全动量G概念以后,有必要对单个微观粒子和其几率波函数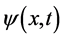 和
和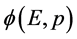 的意义作进一步的讨论。
的意义作进一步的讨论。
5.1. 不同形象微观粒子波函数分析
由前文知道,单个微观粒子非相互作用状态不是三维x空间中沿一定方向运动着边界清晰的“小球”那样一种经典形象,它是三维x空间和能量E空间双波包结构。由于人类客观感知的局限,在三维x空间宏观世界研究的大多是速度 很小的单个运动物体,而该情况其全时间D的标量
很小的单个运动物体,而该情况其全时间D的标量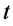 参数的变化是人类最容易察觉的可观测量、全动量
参数的变化是人类最容易察觉的可观测量、全动量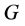 的矢量
的矢量 参数也是人类最容易察觉的可观测量。而进入微观世界当且仅当以参数
参数也是人类最容易察觉的可观测量。而进入微观世界当且仅当以参数 为自变量时,单个微观粒子在三维
为自变量时,单个微观粒子在三维 空间形象才为波函数
空间形象才为波函数 ;与此相对应当且仅当以参数
;与此相对应当且仅当以参数 为自变量时,在三维E空间单个微观粒子形象也才是波函数
为自变量时,在三维E空间单个微观粒子形象也才是波函数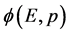 。
。
实际上,自然界客观存在一类微观粒子,当其在静止(速度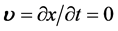 )状态附近运动幅度较小时,动量
)状态附近运动幅度较小时,动量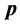 对能量贡献很小E近似为标量其静止能量
对能量贡献很小E近似为标量其静止能量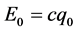 不变,相对时间
不变,相对时间 对
对 贡献也很小,因此x近似为
贡献也很小,因此x近似为 特定静止壳层
特定静止壳层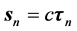 确定。关系式成立:
确定。关系式成立:
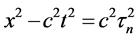 (24)
(24)
 (25)
(25)
该类微观粒子状态改变时仅仅全时间D的 参数显著变化;全动量
参数显著变化;全动量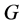 的
的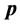 参数显著变化。所以,对该类微观粒子的研究只要考察与其相联系的俩几率波函数
参数显著变化。所以,对该类微观粒子的研究只要考察与其相联系的俩几率波函数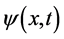 和
和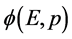 的变化就够了。
的变化就够了。
需要特别注意的是:按大对称考虑自然界还应存在有另一类微观粒子,它们在三维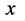 空间的全速度矢量分量
空间的全速度矢量分量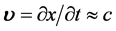 始终运动在高速状态,其标量分量w始终保持非常小
始终运动在高速状态,其标量分量w始终保持非常小 。另一方面,在三维E空间里研究同一微观粒子其速度
。另一方面,在三维E空间里研究同一微观粒子其速度 很小在近似“静止”状态,当其在静止(速度
很小在近似“静止”状态,当其在静止(速度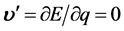 )状态附近运动变化幅度很小时其“静止”参数
)状态附近运动变化幅度很小时其“静止”参数 不变,特定粒子壳层
不变,特定粒子壳层 确定。则满足关系式
确定。则满足关系式
 (26)
(26)
 (27)
(27)
显然,物质内部该类微观粒子运动时仅仅其全动量 的
的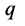 参数显著变化;全时间D的
参数显著变化;全时间D的 参数显著变化。所以,对该类微观粒子的研究只要考察与其相联系的几率波函数
参数显著变化。所以,对该类微观粒子的研究只要考察与其相联系的几率波函数 和
和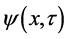 就够了。三维
就够了。三维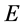 空间里该类微观粒子
空间里该类微观粒子 参数为自变量,
参数为自变量, 参数为因变量。同样的,在三维能量
参数为因变量。同样的,在三维能量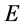 空间波函数
空间波函数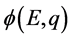 定义域中的每一对确定数E、
定义域中的每一对确定数E、 ,都对应真实存在的三维
,都对应真实存在的三维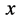 空间中一平面波
空间中一平面波
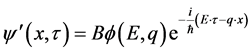 (28)
(28)
在波函数 定义域中的每一对确定数
定义域中的每一对确定数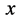 、
、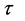 ,也都对应能量
,也都对应能量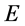 空间中一几率波
空间中一几率波
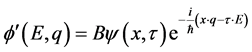 (29)
(29)
实际上,三维x空间人们熟悉的电子的运动满足关系式24、25条件:在原子内部一般电子运动速度分量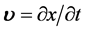 很小,静止能量
很小,静止能量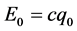 确定,该情况要找寻电子在三维x空间的出现点,只要研究和
确定,该情况要找寻电子在三维x空间的出现点,只要研究和 联带傅立叶变换关系波函数
联带傅立叶变换关系波函数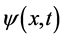 复振幅状态就可以得出正确的结果。假若电子处于静止状态参数
复振幅状态就可以得出正确的结果。假若电子处于静止状态参数 、
、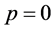 。不难想象,由于某壳层电子
。不难想象,由于某壳层电子 、电子
、电子 不变。当电子吸收一个光子获得参数增量
不变。当电子吸收一个光子获得参数增量 和
和 时,其能量参数和时空参数分别为
时,其能量参数和时空参数分别为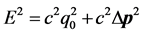 、
、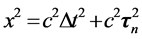 。所以,波函数
。所以,波函数 就是动量变化区间为
就是动量变化区间为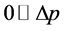 波组的叠加。
波组的叠加。
如果说三维x空间电子的运动满足关系式24、25条件,那我们要问:满足关系式26、27条件的波函数对应着自然界哪一种粒子呢,本文认为它对应着我们熟悉的另一类稳定微观粒子-质子。电子和质子阴阳对称,质子在三维E空间的表现与电子在三维x空间表现相类同,若果真如此它总能让人想起中国古代的阴阳太极图。
5.2. 单个粒子概念与人类时间感觉的原因
单个电子类微观粒子非相互作用状态在三维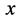 空间作用点
空间作用点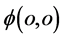 (坐标系原点)看其形象为波函数
(坐标系原点)看其形象为波函数 ;在三维E空间作用点
;在三维E空间作用点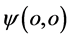 (坐标系原点)看其形象是波函数
(坐标系原点)看其形象是波函数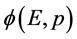 。该电子当和其它粒子发生相互作用(被测量)时,电子波函数
。该电子当和其它粒子发生相互作用(被测量)时,电子波函数 塌缩在碰撞作用点
塌缩在碰撞作用点 相对于点
相对于点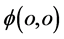 具有了确定的可观测能量E和动量
具有了确定的可观测能量E和动量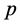 ;与此同时波包
;与此同时波包 塌缩在碰撞作用点
塌缩在碰撞作用点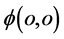 并同步出现在了三维
并同步出现在了三维 空间坐标参考原点上。我们说此时在三维
空间坐标参考原点上。我们说此时在三维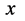 空间坐标系原点(原子原点)观察该电子处于一定态。该定态电子的形象是与其关联的四维s-t空间坐标系原点
空间坐标系原点(原子原点)观察该电子处于一定态。该定态电子的形象是与其关联的四维s-t空间坐标系原点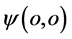 和四维w-p空间坐标系原点
和四维w-p空间坐标系原点 两点之间的两根弦
两点之间的两根弦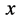 和E。一根弦在s-t空间为
和E。一根弦在s-t空间为

另一根弦在w-p空间可表示为
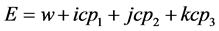
显然,定态的电子具有确定的能量E和全动量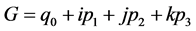 。
。
可以想象一幅图景,定态微观粒子在三维 空间形象可如下描述:弦
空间形象可如下描述:弦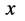 的一头
的一头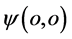 点对应经典粒子“小球”具有能量E和全动量
点对应经典粒子“小球”具有能量E和全动量 ;弦
;弦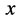 的另一头点
的另一头点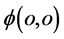 为三维
为三维 空间微观粒子相互作用碰撞点也即宏观粒子三维
空间微观粒子相互作用碰撞点也即宏观粒子三维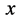 空间“原子”原心,定态粒子在该点参与和其它微观粒子相互作用交换
空间“原子”原心,定态粒子在该点参与和其它微观粒子相互作用交换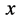 和全时间
和全时间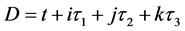 。特别值得注意的是,正是在点
。特别值得注意的是,正是在点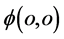 所有参与相互作用的微观粒子的
所有参与相互作用的微观粒子的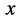 和
和 不断发生变化。也可以想象在该点安装的计时钟表使站在点
不断发生变化。也可以想象在该点安装的计时钟表使站在点 的“观察者”获得了时间
的“观察者”获得了时间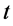 不断“流逝”的感觉。
不断“流逝”的感觉。
比如,在三维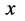 空间中某一电子随机确定的原点
空间中某一电子随机确定的原点 在一原子原心出现后,则该电子的另一原点
在一原子原心出现后,则该电子的另一原点 经历波包塌缩也具有了确定的能量E和全动量
经历波包塌缩也具有了确定的能量E和全动量 。波包塌缩过程也即该电子参与和其他粒子相互作用过程。那么,一次作用事件前后该电子的参数能量
。波包塌缩过程也即该电子参与和其他粒子相互作用过程。那么,一次作用事件前后该电子的参数能量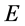 、动量
、动量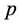 、距离
、距离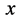 和时间
和时间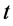 都将发生变化。并且遵守各参与作用粒子在三维
都将发生变化。并且遵守各参与作用粒子在三维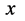 空间碰撞作用点原子原心
空间碰撞作用点原子原心 处交换距离
处交换距离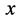 和时间
和时间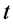 参数,且参与作用粒子总
参数,且参与作用粒子总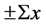 和总全时间
和总全时间 守恒;各参与作用粒子在三维E空间碰撞作用点原子圆心
守恒;各参与作用粒子在三维E空间碰撞作用点原子圆心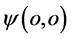 处交换能量E和动量
处交换能量E和动量 参数,且参与作用粒子总
参数,且参与作用粒子总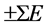 和总
和总 守恒。总而言之,粒子在相互作用状态其原点
守恒。总而言之,粒子在相互作用状态其原点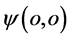 发射或吸收能量(正、负光子),它的另一原点
发射或吸收能量(正、负光子),它的另一原点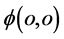 发射或吸收正、负时空子。
发射或吸收正、负时空子。
6. 三维E空间质子类微观粒子运动方程
在量子力学理论中,基于三维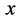 空间微观物质粒子几率波函数
空间微观物质粒子几率波函数 建立了量子力学基础性的薛定谔波动方程[3]
建立了量子力学基础性的薛定谔波动方程[3]
 (30)
(30)
方程30对微观粒子电子及电磁力的研究取得了巨大进展,但对于强相互作用及质子还未能建立起令人满意的理论描述,因此还应该寻求更完备的概念和方法。由前文的讨论知道,质子在三维E空间的表现与电子在三维 空间表现相类同,那么,相同思路就能够基于三维E空间微观粒子几率波函数
空间表现相类同,那么,相同思路就能够基于三维E空间微观粒子几率波函数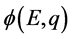 建立起与薛定谔波动方程相对应的三维E空间质子运动方程。试想,对于某一确定的质子,应该有如下两组傅立叶变换关系式成立。
建立起与薛定谔波动方程相对应的三维E空间质子运动方程。试想,对于某一确定的质子,应该有如下两组傅立叶变换关系式成立。

比照电子三维x空间的能量E表达式 ,可以给出三维E空间适合质子的x表达式
,可以给出三维E空间适合质子的x表达式
 (31)
(31)
将31式变形得
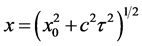 (32)
(32)
由于质子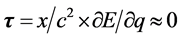 很小,所以上式中
很小,所以上式中 远小于
远小于 。因此可以将式32展开成级数并且只保留前两项得近似式
。因此可以将式32展开成级数并且只保留前两项得近似式
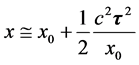 (33)
(33)
显然,上式中 为矢量其方向为质子几率波
为矢量其方向为质子几率波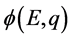 在三维E空间传播方向。基于29和33式并通过和建立三维x空间电子运动方程相似的步骤,应用算符
在三维E空间传播方向。基于29和33式并通过和建立三维x空间电子运动方程相似的步骤,应用算符
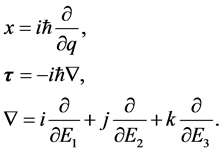
就能够推导出三维v空间静止参数为 的质子波函数
的质子波函数 所满足的微分方程
所满足的微分方程
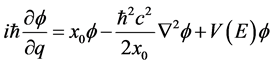 (34)
(34)
同样的,式中 为普朗克常数,c为光速常数。
为普朗克常数,c为光速常数。 为电子方程28式中势场
为电子方程28式中势场 的对应项。显然,新微分方程34式它是一个非相对论协变的微分方程,该方程适用于三维E空间速度
的对应项。显然,新微分方程34式它是一个非相对论协变的微分方程,该方程适用于三维E空间速度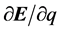 较小也即
较小也即 和
和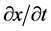 都接近光速c质子的研究。
都接近光速c质子的研究。
7. 微观粒子的电荷与自旋
微观粒子电荷、自旋等概念,这些物理名词已是人类常识,但目前的处境是不借助数学工具仅应用已有物理常识,对微观粒子的这些特性特征很难给出确切定义也很难说出这些概念的深层底蕴。这一节将在本文上面假说的基础上对这些概念做进一步分析,以期对微观物质世界能有更深层次的认识和了解。
7.1. 电子电荷与自旋
由经典物理和量子力学知道,电子和质子分别带有负电荷和正电荷,它们还具有自旋角动量。下面应用本文所提出的一些新概念试图对电荷、自旋等基本概念给出进一步的解释。假若,一低速电子 几率波函数塌缩,波函数
几率波函数塌缩,波函数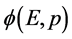 原点
原点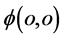 出现在三维x空间参考系原点(原子原点)如图7所示,一定会有三维x空间参考系中距离原点
出现在三维x空间参考系原点(原子原点)如图7所示,一定会有三维x空间参考系中距离原点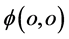 为x的地方波函数
为x的地方波函数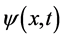 原点
原点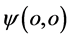 具有了能量E。分析图7点
具有了能量E。分析图7点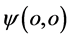 是初始激发电子能量子出现时空点,但是它和三维x空间坐标系原点
是初始激发电子能量子出现时空点,但是它和三维x空间坐标系原点 不是同时的。相对于具有了能量
不是同时的。相对于具有了能量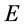 的点
的点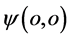 三维x坐标原点
三维x坐标原点 相对时间
相对时间 参数是“正”值。也可以说图7所示电子是“正”t电子。现在让我们想象一幅图景:如若该状况具有了能量
参数是“正”值。也可以说图7所示电子是“正”t电子。现在让我们想象一幅图景:如若该状况具有了能量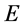 的点
的点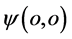 已具有的动量
已具有的动量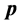 方向由原点
方向由原点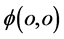 指向
指向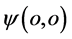 ,则三维x空间与该电子联系的德布罗意波传播方向也由原子原心指向外。因此,可以有规定:在三维
,则三维x空间与该电子联系的德布罗意波传播方向也由原子原心指向外。因此,可以有规定:在三维 空间坐标系中“正”t电子动量
空间坐标系中“正”t电子动量 方向由原点
方向由原点 指向外状态、三维x空间与该电子联系的德布罗意波传播方向也由原子原心向外。我们说具有该特点的电子带“正”电荷显“阳”性。“阳”性电子
指向外状态、三维x空间与该电子联系的德布罗意波传播方向也由原子原心向外。我们说具有该特点的电子带“正”电荷显“阳”性。“阳”性电子 只能在s-t空间“正”t空间范围内出现。它在s-t空间“正”t空间内“吸收”
只能在s-t空间“正”t空间范围内出现。它在s-t空间“正”t空间内“吸收”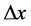 其参数t绝对值增大;它的t绝对值减小时点
其参数t绝对值增大;它的t绝对值减小时点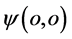 “发射”能量子(光子)其参数E减小。我们称“正”电荷电子为电子的反粒子通常称它叫作“反”电子。
“发射”能量子(光子)其参数E减小。我们称“正”电荷电子为电子的反粒子通常称它叫作“反”电子。
假设一种情况如图7中的“正”电荷电子 出现在
出现在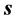 轴上
轴上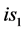 点,该状况电子
点,该状况电子 、动量
、动量 但
但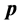 在
在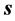 中可以是任意方向,如果该状况电子
中可以是任意方向,如果该状况电子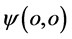 吸收一光子其参数
吸收一光子其参数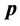 、t不再为零,那么是什么导致
、t不再为零,那么是什么导致 必须往“正”t方向移动呢?我们说自旋角动量是决定性因素。实际上,该静止状态电子波包塌缩双弦为
必须往“正”t方向移动呢?我们说自旋角动量是决定性因素。实际上,该静止状态电子波包塌缩双弦为
 (35)
(35)
 (36)
(36)
可见电子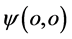 在四维w-p空间坐标系有两个出现点
在四维w-p空间坐标系有两个出现点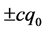 ,出现在
,出现在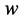 正半轴为
正半轴为 、出现在
、出现在 负半轴为
负半轴为 。静止状态电子
。静止状态电子 在s-t空间中与三维
在s-t空间中与三维 空间任意直线垂直正交,当
空间任意直线垂直正交,当 方向向内用符号⊕表示、当
方向向内用符号⊕表示、当 方向向外用符号⊙表示。因此可以规定:“正”电荷电子
方向向外用符号⊙表示。因此可以规定:“正”电荷电子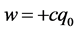 自旋角动量为
自旋角动量为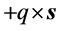 称作左旋;“负”电荷电子
称作左旋;“负”电荷电子 自旋角动量为
自旋角动量为 称作右旋。
称作右旋。
同样的,假若有一电子几率波函数塌缩如图8所示,原子原心点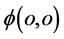 相对于四维s-t空间坐标系原点
相对于四维s-t空间坐标系原点 相对时间参数
相对时间参数 是“负”值且其自旋角动量为右旋,就可以说图8所示粒子带“负”电荷显“阴”性。“阴”性粒子
是“负”值且其自旋角动量为右旋,就可以说图8所示粒子带“负”电荷显“阴”性。“阴”性粒子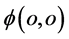 只能在四维s-t空间“负”t空间范围内出现。它“吸收”“负”t空间内的
只能在四维s-t空间“负”t空间范围内出现。它“吸收”“负”t空间内的 其t绝对值增大;它的t绝对值减小时
其t绝对值增大;它的t绝对值减小时 失去能量“发射”光子
失去能量“发射”光子 在s-t空间传播。实际上“负”电荷电子是人类熟悉的自然界地球大量存在的常见电子。
在s-t空间传播。实际上“负”电荷电子是人类熟悉的自然界地球大量存在的常见电子。

Figure 7. The positive charge electronic 3D x space diagram
图7. 正电荷电子三维x空间出现示意图
7.2. 质子电荷与自旋
与对电子的讨论相似,若在三维x空间德布罗意波传播方向由原子原心向外、点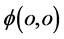 出现在该质子四维s-t“正”t空间、自旋角动量左旋性质的质子带“正”电荷是一般意义上所说的质子,而带“负”电荷的质子通常叫做“反”质子。和电子一样质子的电荷、自旋极性也由其参数
出现在该质子四维s-t“正”t空间、自旋角动量左旋性质的质子带“正”电荷是一般意义上所说的质子,而带“负”电荷的质子通常叫做“反”质子。和电子一样质子的电荷、自旋极性也由其参数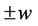 、
、 所决定,但是由于质子和电子存在大对称关系,所以它们的具体表象又有所不同。在三维x空间观察自然界客观存在的原子内部,一般电子运动在距离原心较远处,其
所决定,但是由于质子和电子存在大对称关系,所以它们的具体表象又有所不同。在三维x空间观察自然界客观存在的原子内部,一般电子运动在距离原心较远处,其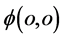 出现在s-t空间
出现在s-t空间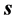 轴附近速度分量
轴附近速度分量 较低状态;质子运动在原心
较低状态;质子运动在原心 附近速度分量
附近速度分量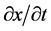 接近光速状态。另一方面假如在三维
接近光速状态。另一方面假如在三维 空间观察原子内部,则质子运动在距离原心较远处,其
空间观察原子内部,则质子运动在距离原心较远处,其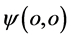 出现w-p空间
出现w-p空间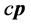 轴附近速度分量
轴附近速度分量 较低状态;而电子运动在原子另一原心
较低状态;而电子运动在原子另一原心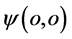 附近速度分量
附近速度分量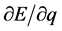 接近光速状态。所以在三维E空间研究质子电荷与自旋可以比照电子在三维x空间相同的方法。
接近光速状态。所以在三维E空间研究质子电荷与自旋可以比照电子在三维x空间相同的方法。
假若,一低速质子 几率波函数塌缩,其波函数
几率波函数塌缩,其波函数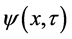 原点
原点 出现在三维E空间中某一点,若以该原子原点为坐标原点建立三维E空间坐标参考系,一定会有在参考系中距离坐标原点为E的地方波函数
出现在三维E空间中某一点,若以该原子原点为坐标原点建立三维E空间坐标参考系,一定会有在参考系中距离坐标原点为E的地方波函数 原点
原点 具有了参数x如图9所示。仔细分析图9可知,被初始激发质子四维w-p空间参考系原点
具有了参数x如图9所示。仔细分析图9可知,被初始激发质子四维w-p空间参考系原点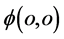 具有了参数x但和三维E坐标系原点
具有了参数x但和三维E坐标系原点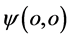 不是同q的。相对于在三维x空
不是同q的。相对于在三维x空

Figure 8. Negatively charged electrons 3D x space diagram
图8. 负电荷电子三维x空间出现示意图
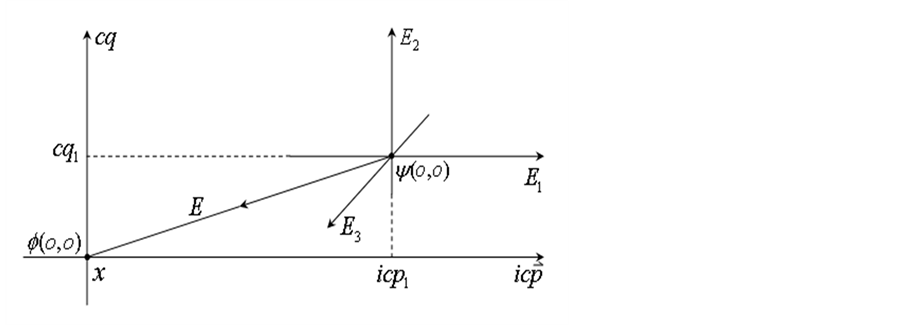
Figure 9. Positively charged protons three-dimensional E space appear diagram
图9. 正电荷质子三维E空间出现示意图
间出现具有了 的点
的点 三维
三维 坐标参考系点
坐标参考系点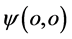 参数
参数 是“正”值。如若该质子
是“正”值。如若该质子 在四维s-t空间运动在“正”
在四维s-t空间运动在“正”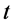 区域,那么其德布罗意波
区域,那么其德布罗意波 在三维E空间传播方向由原心向外、德布罗意波
在三维E空间传播方向由原心向外、德布罗意波 在三维
在三维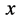 空间传播方向也由原心向外。我们说该质子带“正”电荷、自旋角动量为左旋。反之称之为“反”质子。
空间传播方向也由原心向外。我们说该质子带“正”电荷、自旋角动量为左旋。反之称之为“反”质子。
质子波包塌缩状态也是双弦双原点形象,该状态质子、反质子的双弦为
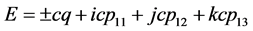 (37)
(37)
 (38)
(38)
自然界中“正”电荷质子显“阳”性,“阳”性质子 只能在w-p空间“正”
只能在w-p空间“正” 空间范围内运动。它“吸收”“正”
空间范围内运动。它“吸收”“正”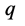 空间内的
空间内的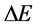 其
其 绝对值增大;它的
绝对值增大;它的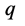 绝对值减小时质子
绝对值减小时质子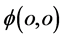 “发射”
“发射” 时空子在三维
时空子在三维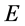 空间传播运动。
空间传播运动。
8. 电子、质子、中子、氢原子和光子
自然界和人类社会的运动规律应该具有相似性。因此,可以将宇宙运行拟人比喻如下:自然界宇宙中,星球类比国家、原子可比人类社会的基本单位——家庭。原子家庭的基本特征是“阴–阳”结构,原子家庭有大有小,但其家庭成员一般由电子(阴)、质子(阳)组成。在三维x空间观察以点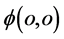 为原点的原子结构电子主外、质子主内,质子(和中子)通常待在原子核内,而电子在外奔波护卫。可以推断:在三维E空间以点
为原点的原子结构电子主外、质子主内,质子(和中子)通常待在原子核内,而电子在外奔波护卫。可以推断:在三维E空间以点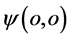 为原点的同一原子也是局限于一小“空间”范围的集团单位,该“空间”集团单位是原子的另一面。自然界最简单的原子家庭是“丁克”一族——氢原子。中子不带电可看作电子和质子的一种特殊“偶合”状态。
为原点的同一原子也是局限于一小“空间”范围的集团单位,该“空间”集团单位是原子的另一面。自然界最简单的原子家庭是“丁克”一族——氢原子。中子不带电可看作电子和质子的一种特殊“偶合”状态。
8.1. 电子
电子是自然界中稳定的微观粒子,双波包塌缩状态电子如图10所示。电子带“负”电荷是“阴”性粒子。可以想象,它和质子相互作用波包塌缩瞬间,站在三维x空间 出现点(原子原心)观察以点
出现点(原子原心)观察以点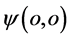 为原心的电子s-t空间,该点电子
为原心的电子s-t空间,该点电子 总是一定出现在s-t空间的“负”
总是一定出现在s-t空间的“负”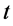 轴空间内见图10(a)。这意思是说,电子的状态无论怎么样变化
轴空间内见图10(a)。这意思是说,电子的状态无论怎么样变化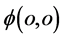 都只能出现在s-t空间的“负”
都只能出现在s-t空间的“负” 轴空间,如若出现在“正”
轴空间,如若出现在“正”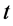 轴空间粒子就不再是原来性质的电子而变为了反电子——“正”电荷电子粒子。
轴空间粒子就不再是原来性质的电子而变为了反电子——“正”电荷电子粒子。
另一方面,电子是人类了解较多的微观粒子之一,假如它在经典静止状态附近运动能量为电子 、
、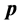 方向不能确定时,该电子
方向不能确定时,该电子 在
在 时刻有可能出现在s-t空间矢量三维
时刻有可能出现在s-t空间矢量三维 空间中任何一点,从图10可以看出该状态电子其双弦为
空间中任何一点,从图10可以看出该状态电子其双弦为
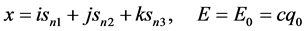
显然,相对于三维x空间原子原心点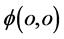 ,具有
,具有 的点电子
的点电子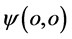 在三维
在三维 空间可能的出现区域是半径为
空间可能的出现区域是半径为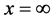 的三维球体,因为普朗克常数
的三维球体,因为普朗克常数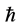 存在的缘故
存在的缘故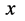 绝对值越小其不连续性越明显。
绝对值越小其不连续性越明显。
实际上,假若图10所示电子 仅能够出现在s-t空间
仅能够出现在s-t空间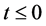 的区域中,且该电子被测量获得一个普朗克常数量子
的区域中,且该电子被测量获得一个普朗克常数量子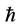 的扰动,双波包出现也即测不准关系成立,
的扰动,双波包出现也即测不准关系成立,

从图10可以看出:电子波包塌缩瞬间,点 在图10(b)
在图10(b)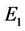 点存在时,点
点存在时,点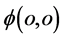 一定存在于在图10(a)
一定存在于在图10(a) 点;点
点;点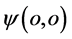 在图10(b)
在图10(b)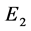 点存在时,点
点存在时,点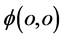 一定在图10(a)
一定在图10(a) 点存在着。显然,如果,微观粒子获得的作用量子数必须为普朗克常数量子
点存在着。显然,如果,微观粒子获得的作用量子数必须为普朗克常数量子 的整数
的整数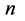 倍成立,而将点
倍成立,而将点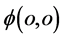 看作三维x空间原子原心、将点
看作三维x空间原子原心、将点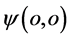 看作三维E空间该原子另一个原心的话,那么,在三维x空间该原子内电子波包塌缩瞬间电子
看作三维E空间该原子另一个原心的话,那么,在三维x空间该原子内电子波包塌缩瞬间电子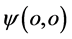 出现点呈“壳层”状态。一般地,对于一特定电子在某一原子内特定“壳层”上出现,电子的参数满足关系式
出现点呈“壳层”状态。一般地,对于一特定电子在某一原子内特定“壳层”上出现,电子的参数满足关系式

也就是说,若电子在某一原子内的“壳层”不变,运动状态的改变其静止能量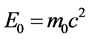 为常数、静止参数
为常数、静止参数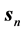 也不变,狭义相对论的基础(
也不变,狭义相对论的基础(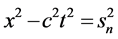 =常数)才能成立。
=常数)才能成立。
8.2. 质子
质子也是自然界中稳定的微观粒子之一。本文认为:在三维x空间质子与电子有着迥然不同的形象如图11所示,它和电子是大对称结构,也就是说,电子在三维x空间的表现和形象与质子在三维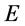 空间的表现和形象一个模样。和电子有不变
空间的表现和形象一个模样。和电子有不变 一样质子也有不变的经典静止状态参数
一样质子也有不变的经典静止状态参数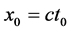 。当质子在三维E空间运动在经典静止状态时x参数为其固定不变值
。当质子在三维E空间运动在经典静止状态时x参数为其固定不变值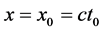 且
且 ,该状态质子点
,该状态质子点 可能出现在w-p空间矢量三维
可能出现在w-p空间矢量三维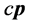 空间中任何一点。从图11可以看出该状态质子静止
空间中任何一点。从图11可以看出该状态质子静止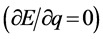 其双弦为
其双弦为
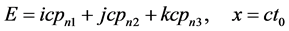
显然,相对于具有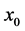 的点
的点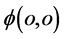 ,点
,点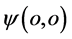 在三维
在三维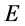 空间中可能的出现区域是半径为
空间中可能的出现区域是半径为 的
的
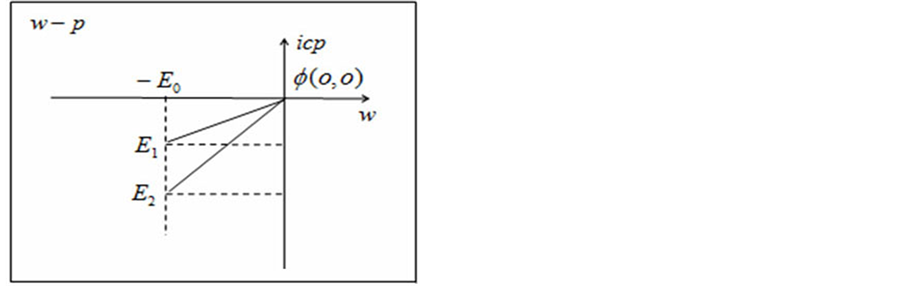

(a) s-t space electronic collapse thumbnail(b) w-p space electronic collapse thumbnail
Figure 10. The electronic wave packet collapse state diagram
(a) s-t空间电子塌缩图(b) w-p空间电子塌缩图
图10. 电子波包塌缩状态示意图


(a) s-t Space proton collapse thumbnail(b) w-p Space proton collapse thumbnail
Figure 11. Proton wave packet collapse state diagram;
(a) s-t空间质子塌缩图(b) w-p空间质子塌缩图
图11. 质子波包塌缩状态示意图
三维矢量球体。
实际上,如若图11所示质子 仅能够出现在w-p空间
仅能够出现在w-p空间 的区域中,且该质子被测量获得一个普朗克常数量子
的区域中,且该质子被测量获得一个普朗克常数量子 的扰动,双波包出现也即测不准关系成立
的扰动,双波包出现也即测不准关系成立
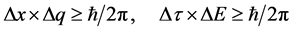
从图11可以看出:质子波包塌缩瞬间在三维 空间原子原心
空间原子原心 观察质子
观察质子 (具有了参数x)出现点也将呈“壳层”状态。并且,若质子在三维
(具有了参数x)出现点也将呈“壳层”状态。并且,若质子在三维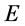 空间某一原子内的“壳层”不变时,其运动状态改变但其静止参数
空间某一原子内的“壳层”不变时,其运动状态改变但其静止参数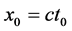 为常数、壳层参数
为常数、壳层参数 为常数,该状况关系式
为常数,该状况关系式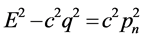 为常数成立。
为常数成立。
8.3. 中子
中子顾名思义是“中”性粒子表现不带电荷,但是,客观实验已然揭示,在一定条件下中子可以衰变为一个质子、一个电子和一中微子。因此,中子可看作电子和质子的一种特殊“偶合”状态,该状态必是“双空间”全方位意义上使“大对称”的电子和质子波函数达到“密切偶合”,以致在原子核内使偶合电子和质子的带电性质(阴\阳特性)不能显现。
合理推断有可能中子是如下一种状态:一个三维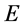 空间经典静止质子和一个三维x空间经典静止电子“密切偶合”,而它们的双弦都呈最短状态(壳层数
空间经典静止质子和一个三维x空间经典静止电子“密切偶合”,而它们的双弦都呈最短状态(壳层数 )。该“密切偶合”状态下电子双弦为
)。该“密切偶合”状态下电子双弦为
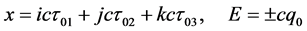
质子双弦为

该状态电子在s-t空间的自旋角动量为

质子在w-p空间的自旋角动量为

实际上,或许可以如下理解组成中子的质子和电子的“特殊偶合”运动状态。该状态下质子倾其所有发射一个大光粒子传给电子吸收;与此同时电子也倾其所有发射一个大“时空粒子”传给质子吸收,这一双向过程完成后原来质子变为了电子、电子变为了质子但它还是中子——旋转了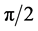 角度的中子。互变的一个质子和一个电子“特殊偶合”整体对外表现为一个中性粒子。中子是“特殊偶合”谐振子。
角度的中子。互变的一个质子和一个电子“特殊偶合”整体对外表现为一个中性粒子。中子是“特殊偶合”谐振子。
8.4. 光粒子和时空子粒子
光子静质量为零,其参数 与动量
与动量 方向重合(静止电子参数
方向重合(静止电子参数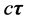 与参数
与参数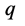 方向垂直正交),在三维
方向垂直正交),在三维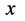 空间波函数
空间波函数 波前传播速度
波前传播速度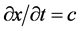 不变。如若其能量
不变。如若其能量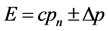 而
而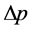 足够小,那么,光子在哪一点出现由动量
足够小,那么,光子在哪一点出现由动量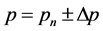 对应波组叠加形成的波函数
对应波组叠加形成的波函数 振幅峰值决定。对于一特定光子与其它粒子相互作用出现被测量状态其双弦为
振幅峰值决定。对于一特定光子与其它粒子相互作用出现被测量状态其双弦为

可见,光子仅能够在三维x空间运动传播,对于光子的全动量、全时间和全速度如下关系式成立。

显然,上式中全速度的虚部 。因此,光能量子和光平面波在三维x空间的传播运动速度相同恒为常数
。因此,光能量子和光平面波在三维x空间的传播运动速度相同恒为常数 。
。
另一方面,前面提到过时空子和光子有着某种对称关系,因此,关于时空子定义如下:时空子是三维E空间传递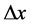 的粒子,它的显著特点是其参数
的粒子,它的显著特点是其参数 与参数
与参数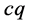 方向平行且
方向平行且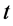 参数、
参数、 参数都为0。对于一特定时空子其
参数都为0。对于一特定时空子其 为常数,在三维
为常数,在三维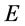 空间和其它粒子相互作用出现瞬时其双弦为
空间和其它粒子相互作用出现瞬时其双弦为
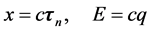
时空子在三维 空间传播如下关系式成立。
空间传播如下关系式成立。
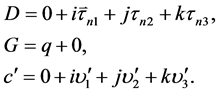
上式中全速度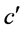 的虚部
的虚部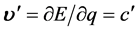 。同样的,时空子平面波动在三维E空间的传播运动速度也恒为常数
。同样的,时空子平面波动在三维E空间的传播运动速度也恒为常数 。
。
一般地,光子和时空子成对产生,光子能量子在三维x空间有两种存在形式,其一,蕴藏在电子类或质子类实物粒子中;其二,光子以能量子形式独立存在。同样的,时空子在三维E空间也有两种存在形式,其一,蕴藏在质子类或电子类实物粒子中;其二,以时空子形式独立存在。
8.5. 氢原子
目前,人们普遍接受的物质原子结构可描述如下:在三维x空间原子由原子核和核外运动的电子组成,原子核位于原子的中心部位。自然界最简单的物质原子氢原子由两个微观粒子组成,氢原子核仅有一个质子,而核外也只有一个电子所环绕。带正电荷的质子和带等同负电荷的电子相互吸引阴-阳结合构成相对稳定的氢原子。
如果,自然界任何微观基本粒子都是双波包双原点(双弦双原点)的波–粒二象结构,那么,在此基础上就能够给出氢原子形象进一步的描述:氢原子由一个质子和一个电子组成。通常在三维x空间,质子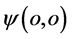 “吸收”
“吸收”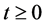 区域内的光能量子处于激发状态带正电荷;电子“吸收”
区域内的光能量子处于激发状态带正电荷;电子“吸收”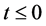 区域内的光子也处于相应激发状态带负电荷。不难想象低激发态氢原子的形象应该是:在三维
区域内的光子也处于相应激发状态带负电荷。不难想象低激发态氢原子的形象应该是:在三维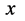 空间电子
空间电子 点的可能出现区域,是以氢原子原心
点的可能出现区域,是以氢原子原心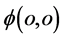 为原点、半径约为
为原点、半径约为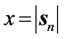 的三维球面附近区域;因为质子
的三维球面附近区域;因为质子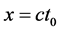 在三维x空间的投影很小,所以它的
在三维x空间的投影很小,所以它的 出现点就在氢原子原心
出现点就在氢原子原心 附近,氢原子内能量越大质子
附近,氢原子内能量越大质子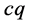 越大时质子在氢原子原心附近活动范围也就越大如图12所示。另一方面,在三维E空间质子
越大时质子在氢原子原心附近活动范围也就越大如图12所示。另一方面,在三维E空间质子 点的可能出现区域是以氢原子另一原心
点的可能出现区域是以氢原子另一原心 为原点、半径约为
为原点、半径约为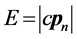 的三维E球面附近;因为该情况下电子
的三维E球面附近;因为该情况下电子 点
点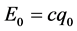 在三维E空间投影很小,所以具有了参数x的电子
在三维E空间投影很小,所以具有了参数x的电子 只能在三维E空间氢原子原心
只能在三维E空间氢原子原心 附近出现,氢原子内能越大电子在其原心附近活动范围也就越大。
附近出现,氢原子内能越大电子在其原心附近活动范围也就越大。
可以想象,氢原子内电子和质子偶合交换作用量子的图景:首先看三维x空间氢原子。第一步,某一“壳层”经典静止电子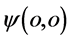 吸收一个三维x空间传播过来的光子
吸收一个三维x空间传播过来的光子 ,电子具有了
,电子具有了 进而
进而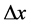 。第二步,该瞬时在电子引力(下一节讨论)作用下通过电子在三维x空间氢原子原心
。第二步,该瞬时在电子引力(下一节讨论)作用下通过电子在三维x空间氢原子原心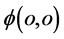 又将
又将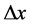 以时空子形式传播向三维E空间同步发射光子。第三步,该电子又重新静止而其弦
以时空子形式传播向三维E空间同步发射光子。第三步,该电子又重新静止而其弦 运动一角度
运动一角度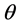 也即其s-t空间完成一次自旋。与此相协调三维E空间氢原子质子也经历相应三步完成一次自旋,第一步,某一“壳层”经典静止质子
也即其s-t空间完成一次自旋。与此相协调三维E空间氢原子质子也经历相应三步完成一次自旋,第一步,某一“壳层”经典静止质子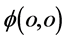 点吸收一个时空子
点吸收一个时空子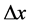 ,质子具有了
,质子具有了 进而
进而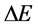 。第二步,该瞬时在质子引力作用下通过质子
。第二步,该瞬时在质子引力作用下通过质子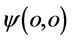 点又将
点又将 光子以速度常数
光子以速度常数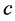 传向三维
传向三维 空间同步发射时空子。第三步,质子重新静止而其弦
空间同步发射时空子。第三步,质子重新静止而其弦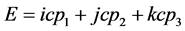 运动一角度
运动一角度 其w-p空间自旋。显然,这一事件在三维x空间
其w-p空间自旋。显然,这一事件在三维x空间

Figure 12. Hydrogen atoms protons and electrons are coupled state diagram
图12. 氢原子质子和电子相互偶合状态示意图
看上去近似是电子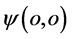 点围绕质子
点围绕质子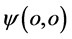 (在原子原心附近出现)旋转;在三维E空间看上去是质子
(在原子原心附近出现)旋转;在三维E空间看上去是质子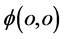 点围绕电子旋转。
点围绕电子旋转。
试想,若一氢原子其电子在三维x空间运动在近似经典静止状态,即核外电子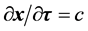 ,
,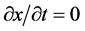 ;质子在三维E空间也运动在经典静止状态其
;质子在三维E空间也运动在经典静止状态其 ,
,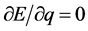 。假设,因故氢原子进入如下一种特殊状态:其一,质子点
。假设,因故氢原子进入如下一种特殊状态:其一,质子点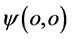 不断持续吸收三维
不断持续吸收三维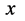 空间自由运动的光能量子使得该原子在三维E空间的质子出现“壳层”向
空间自由运动的光能量子使得该原子在三维E空间的质子出现“壳层”向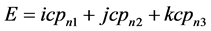 变大方向持续变化,也就是说,质子w-p空间
变大方向持续变化,也就是说,质子w-p空间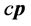 越来越大。因为该状态质子参数
越来越大。因为该状态质子参数 不变
不变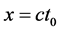 不变、
不变、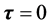 ,所以在三维x空间质子始终只能投影出现在原子原心点周围小范围内且质量
,所以在三维x空间质子始终只能投影出现在原子原心点周围小范围内且质量 持续增大;其二,电子点
持续增大;其二,电子点 持续不断吸收三维E空间时空子使该状态下该原子在三维x空间的电子出现“壳层”向
持续不断吸收三维E空间时空子使该状态下该原子在三维x空间的电子出现“壳层”向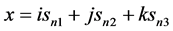 变大方向持续变化,电子在三维x空间
变大方向持续变化,电子在三维x空间 越来越大,因为该状态电子参数
越来越大,因为该状态电子参数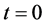 不变
不变 不变、
不变、 。所以在三维E空间电子始终只能投影出现在原子原心点周围小范围内且参数
。所以在三维E空间电子始终只能投影出现在原子原心点周围小范围内且参数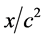 持续增大。可以想象,在三维
持续增大。可以想象,在三维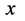 空间观察该原子看到的将是一电子逐渐远离原子原心而质子无限吞噬光子能量子的小“黑洞”。
空间观察该原子看到的将是一电子逐渐远离原子原心而质子无限吞噬光子能量子的小“黑洞”。
9. 电子引力、质子引力和万有引力
物质分子、宏观物体以至星球宇宙由原子、分子组成,而不同种类的原子都是一定数量微观粒子波包相互作用的动态稳定集合。迄今为止,原子在人类头脑中仅仅是其在三维x空间的“形象”;但由前文的讨论有理由认为同微观粒子一样,原子、分子、宏观物体以至宇宙星体还应存在自身的另一面即在三维E空间的动态稳定集合形象。
自然界的确满足简单性原则,电子和质子这两种稳定的微观基本粒子阴—阳结合成为原子,原子组合成分子以致万物、星体和广袤宇宙。因此,本文认为:阴—阳相吸是自然界最基本的运动规律,阴—阳平衡是结构试图达到的目标,作用力既是平衡状态的破坏者也是状态平衡的维护者,从微观到宏观的各层次结构组织在力的作用下,不停演绎着平衡→失衡→新的平衡的运动过程。下面就从双波包双原点(双弦双原点)微观粒子结构模型和自然界最基本的运动规律阴—阳相吸这两点出发,以新的视角对万有引力、质子强作用力和电子电磁相互作用进行一些探索性的讨论。
9.1. 电磁作用——电子引力
由前面的讨论知道,某一电子经典静止状态其双弦为

该状态电子的 和
和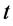 两个参数都为零,具有了静止能量
两个参数都为零,具有了静止能量 的点
的点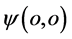 可能出现在三维
可能出现在三维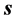 空间任意一点。假若静止状态电子出现在三维
空间任意一点。假若静止状态电子出现在三维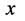 空间如图13所示,图中三维
空间如图13所示,图中三维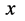 空间原子原心点
空间原子原心点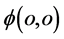 可能出现在电子s-t空间中纯矢量空间内的任意
可能出现在电子s-t空间中纯矢量空间内的任意 点,能量子出现点
点,能量子出现点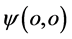 具有了电子静能量
具有了电子静能量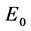 。由全动量公式
。由全动量公式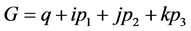 可以看出,因为
可以看出,因为 为零所以静止状态电子全动量的矢量部分
为零所以静止状态电子全动量的矢量部分 为零,但该状态其全动量标量部分q为
为零,但该状态其全动量标量部分q为

显然,由前面全速度概念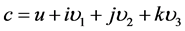 讨论知道,这里所说的“静止”状态电子不是绝对意义上的静止,它仅表示粒子全速度的矢量部分
讨论知道,这里所说的“静止”状态电子不是绝对意义上的静止,它仅表示粒子全速度的矢量部分 等于零,而该状态电子还有一全速度
等于零,而该状态电子还有一全速度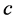 的标量部分
的标量部分 。仔细分析并合理推断,该状态电子的速度
。仔细分析并合理推断,该状态电子的速度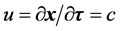 和三维
和三维 空间中任意直线都垂直正交。因此。图13中具有能量
空间中任意直线都垂直正交。因此。图13中具有能量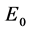 的点
的点 的运动速度
的运动速度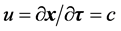 方向和直线
方向和直线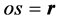 一定也垂直正交。我们说该状态电子具有能量
一定也垂直正交。我们说该状态电子具有能量 的点
的点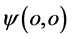 相对于原子原心点
相对于原子原心点 具有一个全速度意义上的加速度
具有一个全速度意义上的加速度
 (39)
(39)
这是一全新的加速度概念,比照经典物理学中匀速 圆周运动物体的加速度
圆周运动物体的加速度
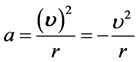
是离心方向,本文认为:式39所给出的加速度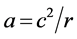 是向心加速度。很明显若电子不在“静止”状态,那么,一般运动状态速度
是向心加速度。很明显若电子不在“静止”状态,那么,一般运动状态速度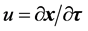 的电子向心加速度可表示为
的电子向心加速度可表示为
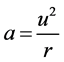 (40)
(40)
考虑到上式中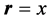 ,所以由40式表示的向心加速度产生的向心力为
,所以由40式表示的向心加速度产生的向心力为
 (41)
(41)
我们称41式F叫做“电子引力”。显然,三维 空间“静止”状态电子且
空间“静止”状态电子且 最小“壳层”的“电子引力”为
最小“壳层”的“电子引力”为
 (42)
(42)
可以想象,42式计算出的“电子引力”是电子可能具有的最大向心力,因为电子在经典“静止”状态 、最小“壳层”
、最小“壳层” 。所以“电子引力”随着电子“壳层”
。所以“电子引力”随着电子“壳层”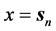 的增大而减小,随着电子
的增大而减小,随着电子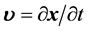 的增大“电子引力”也逐渐减小。显然“电子引力”的方向永远沿x指向三维x空间原子原心
的增大“电子引力”也逐渐减小。显然“电子引力”的方向永远沿x指向三维x空间原子原心 。
。
9.2. 质子强作用——质子引力
因为电子、质子存在大对称关系,所以三维x空间对电子引力的讨论可以推广到原子的另一组成部分——质子。不难想象,若在三维E空间中研究 的“静止”质子,就会发现其速度
的“静止”质子,就会发现其速度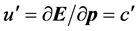 方向和三维
方向和三维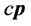 空间中任意直线都垂直正交如图14所示。因此,图14中具有参数
空间中任意直线都垂直正交如图14所示。因此,图14中具有参数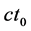 的点
的点 的运动
的运动
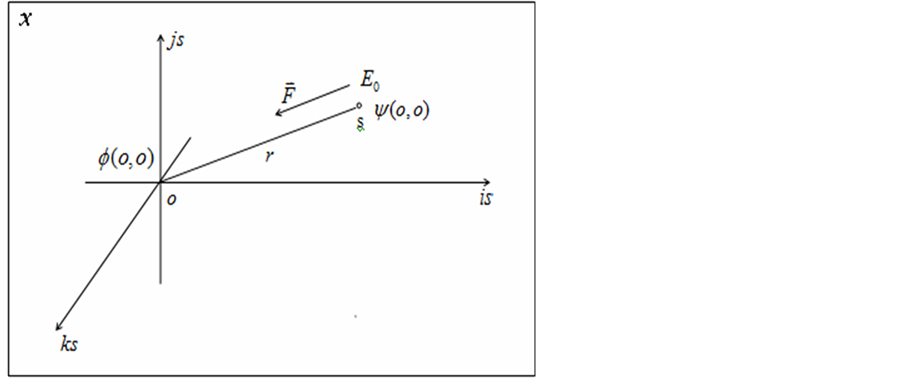
Figure 13. The classical electron rest in three-dimensional s space appear diagram
图13. 经典静止电子在三维s空间出现示意图

Figure 14. “Static” proton in three-dimensional cp space appear diagram
图14. “静止”质子在三维cp空间出现示意图
速度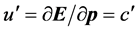 方向和直线
方向和直线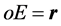 一定是垂直正交的。我们说该状态质子具有了参数
一定是垂直正交的。我们说该状态质子具有了参数 的点
的点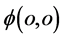 相对于原子原心点
相对于原子原心点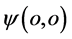 有一个加速度
有一个加速度
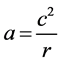
本文认为:上式所给出的加速度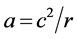 是三维
是三维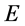 空间(w-p空间)一种可类比的向心加速度。它能产生一种三维E空间对原子原心点
空间(w-p空间)一种可类比的向心加速度。它能产生一种三维E空间对原子原心点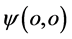 的向心作用,从量纲关系可推断这一向心作用是三维x空间作用力
的向心作用,从量纲关系可推断这一向心作用是三维x空间作用力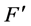 的倒数
的倒数

因此,可以说三维E空间质子“静止”状态 最小“壳层”情况下,反映在三维x空间原子内质子的向心作用力
最小“壳层”情况下,反映在三维x空间原子内质子的向心作用力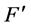 我们称之为三维
我们称之为三维 空间“质子引力”
空间“质子引力”
 (43)
(43)
比较式43和式42不难看出,如若确定原子内质子 远大于电子静能
远大于电子静能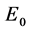 、而质子静止常数
、而质子静止常数 又远小于电子
又远小于电子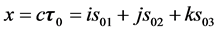 ,那么,质子三维
,那么,质子三维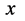 空间指向原子原心
空间指向原子原心 的向心力“质子引力”
的向心力“质子引力” 就远远大于“电子引力”
就远远大于“电子引力”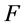 。
。
这里需要对三维 空间原子的形象进一步仔细分析,以氢原子为例假若其质子在三维E空间“壳层”
空间原子的形象进一步仔细分析,以氢原子为例假若其质子在三维E空间“壳层”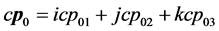 最小、且
最小、且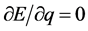 “静止”状态;电子在三维x空间“壳层”
“静止”状态;电子在三维x空间“壳层”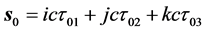 也最小、且
也最小、且 经典“静止”状态,如上状态的氢原子在三维x空间的形象应该是:电子
经典“静止”状态,如上状态的氢原子在三维x空间的形象应该是:电子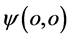 出现在距离原子原心
出现在距离原子原心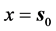
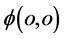 的点其速度
的点其速度 静止状态;质子
静止状态;质子 出现在距离原子原心
出现在距离原子原心 的点
的点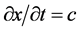 其速度
其速度 在最大状态,由于该状态质子
在最大状态,由于该状态质子 但
但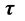 和
和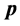 方向平行、
方向平行、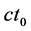 和
和 垂直,所以质子出现点
垂直,所以质子出现点 的投影与三维
的投影与三维 空间原子原心点
空间原子原心点 重合。我们说静止电子是点电子它是完全电压形象电单极子;
重合。我们说静止电子是点电子它是完全电压形象电单极子;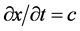 速度
速度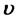 在最大状态的质子是完全电流形象的电单极子。当质子吸收能量子、时空子速度
在最大状态的质子是完全电流形象的电单极子。当质子吸收能量子、时空子速度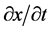 小于光速
小于光速 、
、 大于0也即
大于0也即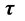 绝对值大于0时,质子出现点
绝对值大于0时,质子出现点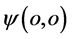 的投影与三维
的投影与三维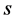 空间原子原心点
空间原子原心点 不再重合而分开,速度矢量
不再重合而分开,速度矢量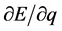 增大伴随着“质子引力”减小。但是“质子引力”方向永远由质子
增大伴随着“质子引力”减小。但是“质子引力”方向永远由质子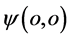 点沿E指向三维x空间原子原心
点沿E指向三维x空间原子原心 。“质子引力”是将强子团结在三维x空间原子原心的决定因素,该作用力就是通常所说的强作用力。
。“质子引力”是将强子团结在三维x空间原子原心的决定因素,该作用力就是通常所说的强作用力。
9.3. 万有引力
万有引力是宏观星体之间的作用力。万有引力存在的根本“依据”应该是“电子引力”和“质子引力”。由前面的讨论我们知道,三维x空间某星体的组成部分——原子内的电子在一定条件下,有可能和远方另一星体的组成部分——原子内的质子相互作用阴–阳相吸,因为在三维x空间“电子引力”是长程力;另一方面,三维E空间某星体的组成部分——原子内的质子在一定条件下,可以和E远方另一星体的组成部分—分子或原子内只能运动在原子原心附近的电子相互作用阴–阳相吸;当然大部分电子、质子只能在本星球内运动不和远方发生关系,能够走出去和远方星体有联系的电子、质子仅是少数粒子。一般地跨星系发生关系的可能性与星体含有物质的多少成比例。星体质量越大跨星系发生关系的粒子总量就会越多、两星体三维x空间距离x绝对值越小跨星系发生关系的粒子之间的强度就越大。因此我们认为:宏观星体之间的作用力——万有引力是跨星系发生关系的巨量微观粒子电子、质子阴–阳相吸的一种叠加效应。果真如此的话,万有引力不应仅仅同星体的质量大小和星体之间的距离有关系,还应该和组成星体的物质类别、结构形态等性质有关系,因为所有这些都决定着电子、质子有否能力和机会走出自己的星球和远方的粒子阴–阳相吸相互作用。
10. 结语
二十世纪物理学取得了巨大进展,但新的理论被实验证实并大量应用于技术领域的同时,一些问题始终困扰着人们挥之不去,诸如量子力学的波–粒二象性问题的费解;狭义相对论理论基础常遭指责未经任何证明就将光速不变原理引进理论;还有自然界物质之间四种相互作用力统一问题等等,近几十年来人们为求寻答案进行着艰苦的探索。本文提出的双波包双原点(双弦双原点)微观粒子结构模型也是这种探索的尝试之一。以三维x空间、s-t空间和三维E空间、w-p空间为基础,以微观粒子新结构模型为着眼点提出了一些全新的概念,虽然这些概念的正确与否还须进一步推敲和验证,但它确实能够从物理上拓展和丰富我们的想象空间,它们或许使人们对物质世界认识的逐步深化有帮助。诚然,要接纳这些新概念还须头脑中已有的许多物理观念做出修正或变革,也只有这样才能理解这个现在看来不可思议的模型形象和全时间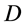 、全动量
、全动量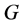 等新概念。但我感觉新模型的确指出了一个新的观察点,通过该观察点看过去,诸多令人费解的问题变得易于理解,微观物质世界的更多方面得以直观展现。
等新概念。但我感觉新模型的确指出了一个新的观察点,通过该观察点看过去,诸多令人费解的问题变得易于理解,微观物质世界的更多方面得以直观展现。
参考文献 (References)
- [1] 周世勋 (1979) 量子力学教程. 人民教育出版社, 北京.
- [2] A.爱因斯坦 (1979) 相对论的意义. 科学出版社, 北京.
- [3] E.H.威切曼 (1978) 量子物理学. 科学出版社, 北京.