Computer Science and Application
Vol.06 No.07(2016), Article ID:18140,9
pages
10.12677/CSA.2016.67053
Review on New Mathematical and Mechanical Models for the Computer Simulation of Vocal Cord
Jinxiao Huang
Electronic Information Engineering College, Qingdao University, Qingdao Shandong

Received: Jul. 5th, 2016; accepted: Jul. 26th, 2016; published: Jul. 29th, 2016
Copyright © 2016 by author and Hans Publishers Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/



ABSTRACT
A review on new mathematical and mechanical models of the vocal cords is given. The basic model is a two-mass nonlinear oscillator system which is accepted to be the basic one for mechanical description in voice production. The model is not only extended into three, five, and more mass systems, systems with time variable parameters and three-dimensional systems, but also simplified into one-mass system with coupled two-direction deflection and damping functions. The corresponding mathematical models are the systems of coupled second-order differential equations which describe the vibrations of the symmetric and asymmetric vocal folds. The models give the conditions for the regular and irregular motions like bifurcation and deterministic chaos in vocal folds. The obtained results are of special interest for detecting the pathology of vocal cords, when there is no visual effect of disease. Based on the results given in the paper, the objectives for future investigation in this matter are given.
Keywords:Mathematical Models, Mechanical Models, More Mass Systems, Two-Direction Deflection

声带计算机仿真的新型数学–力学模型综述
黄金潇
青岛大学电子信息学院,山东 青岛

收稿日期:2016年7月5日;录用日期:2016年7月26日;发布日期:2016年7月29日

摘 要
本文综述了目前声带仿真模型研究的新型数学模型和力学模型。基本模型是一个双质量块非线性振动系统,该系统被认为是一种基本发音过程的力学描述。声带模型不仅可以扩展为三质量块系统、五质量块系统和多质量块系统,也可以扩展为随时间变化而导致参数不同的系统,或者是三维系统。另外,还可以简化成一个具有双向偏转和具有阻尼功能的耦合系统。相应的数学模型对应的二阶微分方程系统,描述了对称和非对称声带的振动。以上这些模型给出了规则和不规则运动的条件,这些运动发生在声带的分叉点,或者是确定性混沌状态。当我们不能从视觉上看出有疾病时,实验得出的结果使得检查声带的病理状态有特殊的意义。根据文中给出的结果,在未来进行这项研究是一个可以实现的目标。
关键词 :数学模型,力学模型,多质量块系统,双向偏转

1. 引言
近年来声带的计算机仿真技术 [1] 被用于喉科疾病的诊断,可以利用人声带的发音功能 [2] ,采用声学分析法来反映出声带的病变。对声带振动模型的研究 [3] 可以揭示出声带振动的特性,有助于理解声带振动的机理。这为喉病理学、人工器官、嗓音治疗等医学领域的研究具有理论指导意义和实际应用价值。
研究人员目前也一直都在试图模仿人类的声音产生,不仅开发各种力学和数学模型来描述与声音产生相连的人体器官,也研究发声的过程。从本质上说,声音是由位于喉部两个侧对的声带运动产生 [4] ,这种运动是由肺产生并通过气管引起的空气流动引起的。声带的复杂性 [5] ,其组织学、形状、位置等等,使我们必须以不同的方式分析具体问题。模拟发声过程现在已有许多的论据,还有很多的问题需要被研究,现在也已经有很多的研究结果发表出来。本文主要的目的不仅是给出关于新型声带计算机仿真模型的综述,而且是对这个研究方向未来的改进给出分析。其中,包括非线性系统的相关属性的引入。
2. 单质量块声带模型
最早的声带振动模型研究是单质量块模型 [6] 。其中一个最简单的模型是单自由度的单质量块模型,这个模型最早是由Flanagan博士提出的,后来由许多相关领域的研究者进行了研究。Flanagan博士用电声学分析法 [7] 描述了声带的动力学知识,提出了单质量块振动系统的声带模型,该模型的自激振动是由随压力的变化而变化的空气流引起的。通过实验观察和总结可以得出这种声带模型的自激力。这种模型是线性的,而且可以有效地解释声带的运动学振动特性。但不足的是,这种模型还不足以解释声带自激力的原理。
在单质量块振动系统的声带模型基础上,Adachi博士等人 [8] 假设了随着空气流向,声带存在平行和垂直两个方向的振动。随后,双自由度的单质量块声带模型被提出了。当质量块运动时,可以用一个不标准的平行四边形来模拟声带,它在摆动的同时也伴随着伸缩性的运动。当把运动的阻尼间隔考虑进去,系统则具有两个霍普夫分叉点和三个周期倍化的分叉点。这个阻尼间隔 [9] ,可以分别用固定的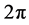 周期和
周期和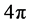 周期来描述。所以存在多种研究方案,甚至可以用不稳定的谐波或者次谐波解决方案来研究。不管是用哪种方案的双自由度单质量块模型,都可以在一个较宽的领域内成功地模拟声带的自激振动。但是由于采用单一质块模型,对声带这种具有不规则形状、有一定弹性和韧性的物理对象来说,不能反映出其运动的细节特征,因此现代声带振动仿真模型采用多质块来加以改进。
周期来描述。所以存在多种研究方案,甚至可以用不稳定的谐波或者次谐波解决方案来研究。不管是用哪种方案的双自由度单质量块模型,都可以在一个较宽的领域内成功地模拟声带的自激振动。但是由于采用单一质块模型,对声带这种具有不规则形状、有一定弹性和韧性的物理对象来说,不能反映出其运动的细节特征,因此现代声带振动仿真模型采用多质块来加以改进。
3. 对称声带的非线性双质量块模型
Lucero和Koenig [10] 将声带组织的非线性特性,引入到声带的基本双质量块模型中,提出了一种改进的对称声带的非线性双质量块模型。
在该模型中,假定两个声带相同,并以相对声门中线对称地运动。当声门是开放的,声带运动的等式可写为:
 (3.1)
(3.1)
其中 是从静止位置
是从静止位置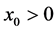 测量的位移。在这种模型中,Lucero和Koenig引入了生物组织弹力 [11] 的立方特点:
测量的位移。在这种模型中,Lucero和Koenig引入了生物组织弹力 [11] 的立方特点:
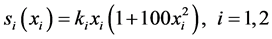 (3.2)
(3.2)
另一方面,对于阻尼力,不使用通常的线性项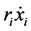 ,而使用非线性特性:
,而使用非线性特性:
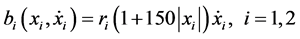 (3.3)
(3.3)
采用非线性项原因是当声门宽度增加的时候,有必要限制声带振动的幅度,以保证仿真的有效性。对于这种情况,存在相对的声带之间的接触,在静止位置上,这两个质量块都在距离远处声门中线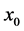 处。然后,在位移
处。然后,在位移 的位置,质量块与它相对的一块碰撞。在接触过程中,引起刚度增加:
的位置,质量块与它相对的一块碰撞。在接触过程中,引起刚度增加:
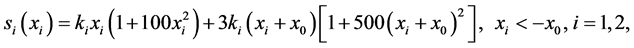 (3.4)
(3.4)
当声门打开的时候如果阻尼系数的值为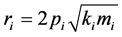 ,通过质量块之间的碰撞,对于给定的阻尼比
,通过质量块之间的碰撞,对于给定的阻尼比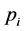 ,可假设:当通过给阻尼比加1时,阻尼系数
,可假设:当通过给阻尼比加1时,阻尼系数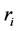 增加了。这个低维声带模型 [12] ,可以再现声带振动的开启和闭合模式。这种模式可以通过对说话时的观测实验得到。
增加了。这个低维声带模型 [12] ,可以再现声带振动的开启和闭合模式。这种模式可以通过对说话时的观测实验得到。
4. 非对称声带的双质量块模型
Isshiki [13] 等人讨论了非对称声带张力的临床意义,不对称可能意味着声带的病理,病变的力学性能和不对称声带的不稳定性,从定性上可能会导致喉部产生不同的声音。在动态模型中包含一些典型的效果,比如左右两声带之间的张力不平衡而造成的影响。
在此基础上,Steineck和Herzel [14] 研究出的非对称声带模型,是基于双质量块模型建立的,见图1。如前面所说的,上下质量块的运动微分方程保持相同,但左声带和右声带是不对称的,存在各种各样的运动。可以用下面的二阶微分方程来表述:
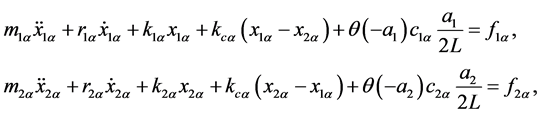 (4.1)
(4.1)
其中,
 (4.2)
(4.2)
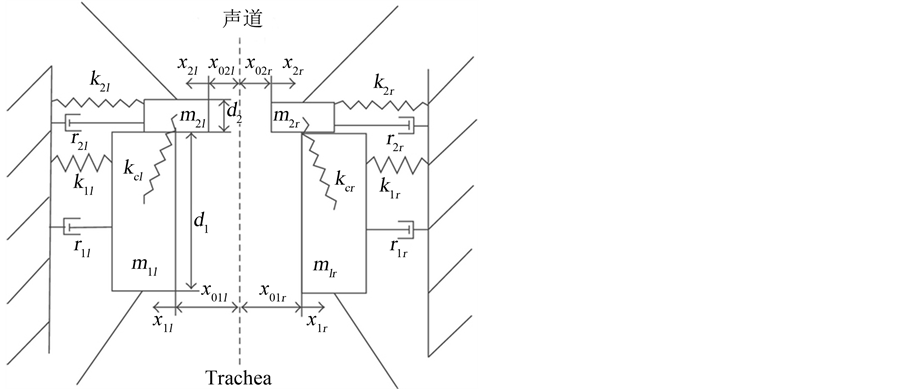
Figure 1. Model of the asymmetric vocal folds
图1. 非对称声带模型
由驱动力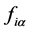 的方程可以看出,通常假定空气流分离位置是在最小区域点,其中即时压降为零。它会导致,对于所有的声门配置,驱动力
的方程可以看出,通常假定空气流分离位置是在最小区域点,其中即时压降为零。它会导致,对于所有的声门配置,驱动力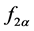 都会变为0。声带的下驱动力,式(4.3)可以表示为:
都会变为0。声带的下驱动力,式(4.3)可以表示为:
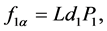 (4.3)
(4.3)
其中是可根据伯努利定律得出的压力:
 (4.4)
(4.4)
是声门的体积流量。对于
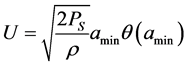 (4.5)
(4.5)
压力是:
 (4.6)
(4.6)
使用非对称声带模型,式(4.1),许多不规则的运动和分叉点可能发生在某些特定的参数值时。不同刚度值的左右声带和临界张力不平衡会导致不同的声带振动模式:次谐波振动、双频率振动(双发声模式)和分布式或嘶哑式发声紊乱。这些不规则模式通常由左声带和右声带之间结构的不对称引起的。模型的正确性已经通过单侧喉部麻痹 [15] [16] 实验被证实。对于单面息肉的情况,声带的振动也是不规则的,也就是所说的混沌模式 [17] [18] 。
利用式(4.1)的这种模型,Zhang [19] 最近调查了不对称的发声系统。他们分析了在自激振荡声带模型中的振动,自激振荡声带模型是中间层刚度左右不对称的。尽管两个质量块的振动频率比接近1:3,但是次谐波同步性在非同步模型中仍是观察不到的。然而振动行为是一个质量块力度控制的,另一个质量块是被迫使在相同的频率振动。逐渐增加的声门下气压导致了两质量块之间相互作用的一种转变,导致了振动模式和频率的突然变化。通过对模型进行了声带振动不对称性 [20] 的测量,获得了对振动不对称特性的比较,可以看出尽管模型是双质量块的,结果仍是有可比较的意义。
5. 非对称声带的非稳定双质量块模型
声带振动的常规临床检查是在静止持续的发声下做出的。然而,这个结论来自一个稳定发声,它仅限于观察到稳态振动声带,不能推广到声音在说话时的运行机制。声带振动的分类是一个关于客观评价嗓音疾病的重要工作。基于双质量块模型的方法适用于分析和定量解释非平稳声带振动。为了模拟非平稳振动,最初常量参数被修改为与时间有关的参数 [21] ,如图2所示。
该图说明了不同时间变量参数下非对称声带的双质量块模型 [22] ,相应的数学模型是一个四耦合微分方程的系统:
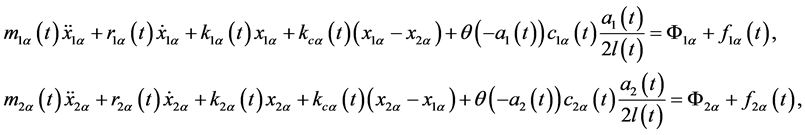 (5.1)
(5.1)
对比式(5.1)和式(4.1),很明显,方程式的形式是相同的。但是在(5.1)中,参数是随时间变化的,并且新引入了反应力。在此系统中,质量是时间变量的函数,反应力 [23] - [25] 被定义为:
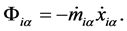 (5.2)
(5.2)
阻尼系数是:
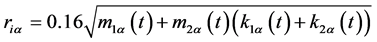 (5.3)
(5.3)
该模型适用于研究非平稳发声。研究结果能够给声带不稳定性做出直观评估 [26] ,可以用在不对称特性的客观量化。非平稳的声带振动对许多语音疾病都具有典型性。也就是说,模型的微调需要由两方面决定,一是不对称系数的时变性 [27] ,二是参数离标准集的偏差 [28] 。
6. 非对称声带的多质量块模型
早先提到的模型普遍化最近由Yang等人 [29] 提出,结合了双自由度的单质量块系统和一个双质量块系统,这个双质量块系统的每一个质量块有一个自由度能扩展到五质量块系统,而这个五质量块系统的每一个质量块又有三个自由度 [30] :不止是在横向和纵向这两个方向上(二维模型) [31] ,而且有垂直振动,如图3。
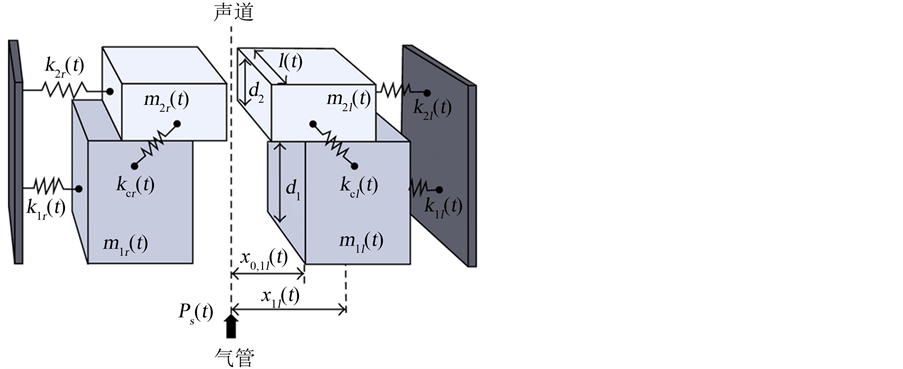
Figure 2. Two-mass models of the asymmetric vocal folds with time variable parameters
图2. 随时间变化参数的非对称声带的双质量块模型
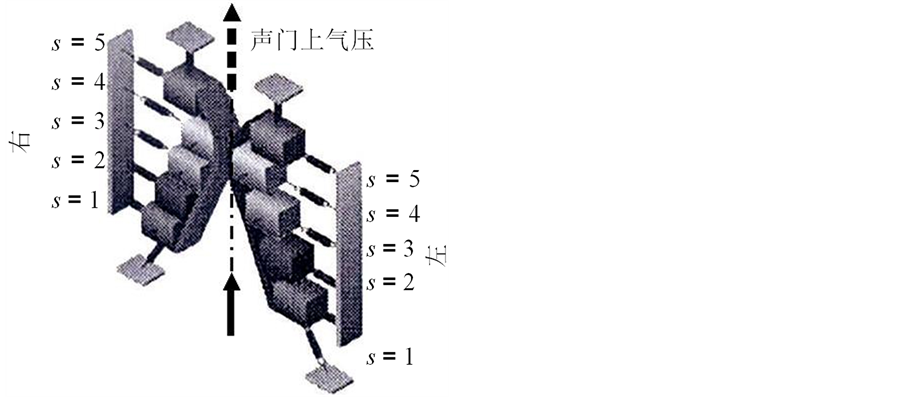
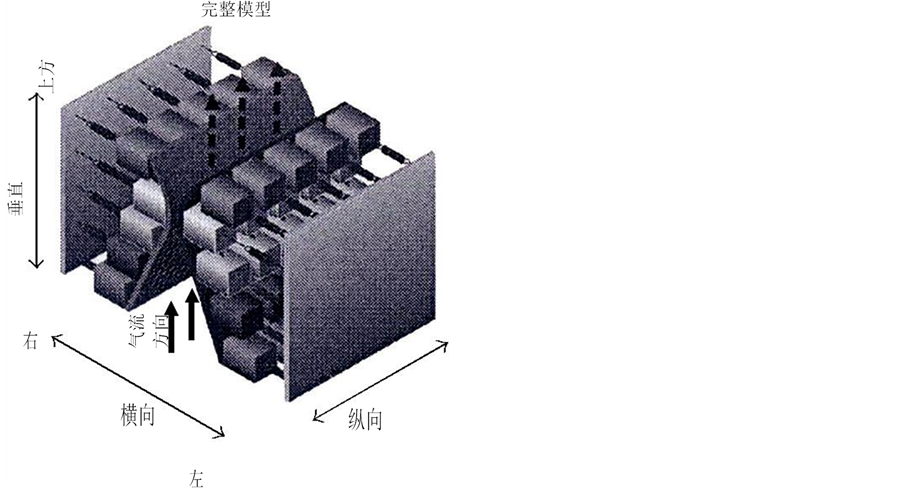
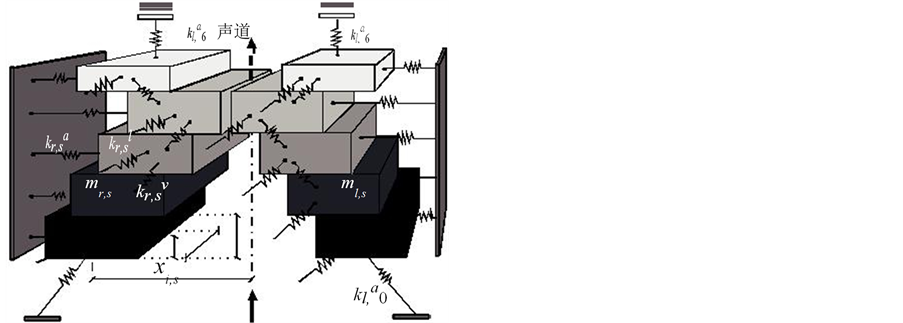

Figure 3. Three-dimensional model of voice folds
图3. 声带的三维模型
这个模型是最突出的特点是,它描述了人类的发声源来自于从声带的三维(3D)振动。这个3D系统的数学模型,五个质量块在左侧(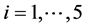 ),5个质量块在右侧(
),5个质量块在右侧(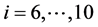 ),数学方程式如下:
),数学方程式如下:
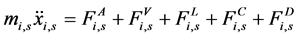 (6.1)
(6.1)
其中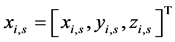 表示每个质量元素在笛卡儿坐标系统的位置,
表示每个质量元素在笛卡儿坐标系统的位置,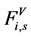 是垂直力耦合,它是声带组织在竖直方向的内力,
是垂直力耦合,它是声带组织在竖直方向的内力,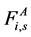 是锚力,它充当甲杓肌在横向方向上的函数。
是锚力,它充当甲杓肌在横向方向上的函数。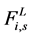 是纵向力耦合,它描述了甲杓肌和声音韧带在纵轴方向的反应。
是纵向力耦合,它描述了甲杓肌和声音韧带在纵轴方向的反应。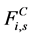 是声带发声时两者之间的碰撞行为,导致声带弹性结构的形变,
是声带发声时两者之间的碰撞行为,导致声带弹性结构的形变,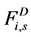 是流体动力。
是流体动力。
连接质量块到固定体的锚力 [32] ,以及质量块之间的垂直和纵向耦合内力,这两种力应该是非线性偏转函数的形式。模型中也包含了碰撞冲击力,也研究了气动力的影响会导致声带的三质量元件振荡。伯努利类型的驱动力是由声门流产生的,从肺始发,作用于声带,从下级到上级,逐步通过整个喉部。此驱动力,不仅取决于该声门下压力,还取决于一些相关的声带几何尺寸(声带的厚度、声带的长度、是否在静止位置)。通过对该模型的研究,发声在对称和非对称的振动期间,使人类声带的三维动态可视化成为可能。
7. 非固定的声带多质量块模型
通过优化时间模型参数,参数随时间变化的多质量块模型可以与从背侧、中间、内侧提取的声带振动相匹配 [33] 。该参数作为客观测量,用于定量评估振幅的左右不对称和在声带中间部分的相位变化,以及沿着声带边缘的前后纵向不对称。背侧、中间、腹侧声带部位的振动行为为描述振动模式提供了信息。在图4中,多质量块时变模型图描述了系统中每一个质量块的纵向和横向振动。
在运动的两个方向上,模拟非对称声带的质量块系统的振动方程如下:
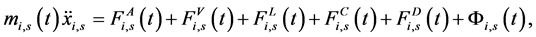 (7.1)
(7.1)
其中,时间变量的质量元素表示为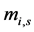 ,在左边
,在左边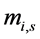 参数
参数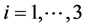 ,在右边参数
,在右边参数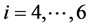 。对于位置较低的质量块,s = 1,较高的质量块,s = 2。
。对于位置较低的质量块,s = 1,较高的质量块,s = 2。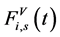 是垂直力耦合,它来自于于从上部和下部之间的质量块连接。假设不存在垂直方向的运动,
是垂直力耦合,它来自于于从上部和下部之间的质量块连接。假设不存在垂直方向的运动,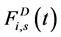 给出了横向和纵向振动之间的联系。
给出了横向和纵向振动之间的联系。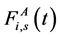 是锚力,它是刚度和阻尼系数的函数。
是锚力,它是刚度和阻尼系数的函数。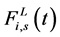 是纵向力,是耦合刚度和阻尼系数的函数。而
是纵向力,是耦合刚度和阻尼系数的函数。而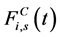 是两个声带之间的碰撞力。与质量块变化相关的反应力是
是两个声带之间的碰撞力。与质量块变化相关的反应力是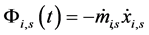 。
。
与时间有关的参数图给出了关于非对称实际运动维度的直观图示。基于参数的评价结果提供了一种分类方法,可以分为正常声带振动和病理声带振动两种情况。
8. 总结
根据以上研究结果,可以得出结论:声带振动的数学模型对于病理现象给出了非常好的定性描述。尽管可以适用于建模,但是所获得的研究结果和真实情况也有定量的差别,现在仍然需要提高模型的准确性。
(1) 在这些数学模型中,声带的非线性属性必须包括在内。微分方程有一些整数和非整数阶次的非线性项。不仅数值型的,而且近似解析方法也可以用来开发利用以解决这些微分方程。
(2) 对于系统中所有模拟声带的质量块,应该分为三个方向的运动:横向,纵向,和垂直。如果能有这样一个完全符合要求的模型,对于声带振动会给出一个更好的解释。
(3) 声带模型中,负库仑阻尼假定为线性的。为了改进模型,我们建议引入整数或非整数阶次的非线性阻尼,这个建议是经过了多次诊断测量的经验而提出,这样的模型将会给更准确的结果。为了解决运动的微分方程,必须延伸一些分析方法,也必须开发一些新的解决方法。
(4) 非平稳的声带振荡对许多语音障碍是比较典型的,其稳定性需要更深入的分析。
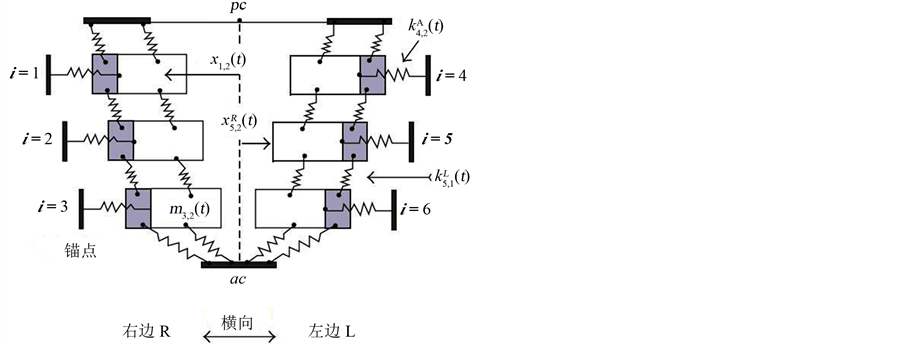
Figure 4. Multimass model of the vocal folds
图4. 声带振动的多质量块模型
(5) 特别注意的有:不规则声带的运动模型、这些运动的微分方程的定性和定量分析描述。声带的不稳定和不规则运动可能意味着疾病或异常。
(6) 声带振动的发生机理与很多学科的发展都息息相关,比如:喉病理学、人工器官、语音识别、语音合成、神经动力学等等。在声带振动原理方面的研究对喉科疾病的非侵入诊断、嗓音保护、歌唱声学、嗓音医学等等有非常重要的意义,对语音识别与合成、语音通信、人机对话以及其他语音产品的开发和产品质量的改善也具有非常广阔的研究前景。
文章引用
黄金潇. 声带计算机仿真的新型数学–力学模型综述
Review on New Mathematical and Mechanical Models for the Computer Simulation of Vocal Cord[J]. 计算机科学与应用, 2016, 06(07): 434-442. http://dx.doi.org/10.12677/CSA.2016.67053
参考文献 (References)
- 1. 赵力. 语音信号处理[M]. 北京: 机械工业出版社, 2007.
- 2. Adachi, S. and Yu, J. (2005) Two-Dimensional Model of Vocal Fold Vibration for Sound Synthesis of Voice and Soprano Singing. Journal of the Acoustical Society of America, 117, 3213-3224. http://dx.doi.org/10.1121/1.1861592
- 3. Wurzbacher, T., Schwarz, R., Döllinger, M., Hoppe, U., Eysholdt, U. and Lohscheller, J. (2006) Model-Based Classification of Nonstationary Vocal Fold Vibrations. Journal of the Acoustical Society of America, 120, 1012-1027. http://dx.doi.org/10.1121/1.2211550
- 4. 王宏, 潘金贵. 基于共振峰增强的语音信号共振峰频率估计[J]. 计算机应用与软件, 2008, 25(11): 140-142.
- 5. 杨顺安. 面向声学语音学的普通话语音合成技术[M]. 北京: 清华大学出版社, 2003.
- 6. Mehta, D.D., Deliyski, D.D., Quatieri, T.F. and Hillman, R.E. (2011) Automated Measurement of Vocal Fold Vibratory Asymmetry from High-Speed Videoendoscopy Recordings. Journal of Speech, Language, and Hearing Research, 54, 47-54. http://dx.doi.org/10.1044/1092-4388(2010/10-0026)
- 7. Cronjaeger, R. (1978) Die Entstehung des primaeren Stimmklangs im menschlichen Kehlkopf—Ein Modell. Ph.D. Dissertation, University of Braunschweig, Braunschweig.
- 8. Fulcher, L.P., Scherer, R.C., Melnykov, A., Gateva, V. and Limes, M.E. (2006) Negative Coulomb Damping, Limit Cycles, and Self-Oscillation of the Vocal Folds. American Journal of Physics, 74, 386-393. http://dx.doi.org/10.1119/1.2173272
- 9. 吴永忠. 基于物理模型的声音合成技术理论研究[D]: [博士学位论文]. 合肥: 合肥工业大学, 2003.
- 10. Lucero, J.C. and Koenig, L.L. (2005) Simulations of Temporal Patterns of Oral Airflow in Men and Women Using a Two-Mass Model of the Vocal Folds under Dynamic Control. Journal of the Acoustical Society of America, 117, 1362-1372. http://dx.doi.org/10.1121/1.1853235
- 11. Onerci, T.M. (2010) Diagnosis in Otorhinolaryngology, Springer, London. http://dx.doi.org/10.1007/978-3-642-00499-5
- 12. Flanagan, J.L. (1968) Source-System Interaction in the Vocal Tract. Annals of the New York Academy of Sciences, 155, 9-17. http://dx.doi.org/10.1111/j.1749-6632.1968.tb56744.x
- 13. Isshiki, N., Tanabe, M., Ishizaka, K. and Broad, D. (1977) Clinical Significance of Asymmetrical Vocal Cord Tension. Annals of Otology, Rhinology and Laryngology, 86, 58-66.
- 14. Steinecke, I. and Herzel, H. (1995) Bifurcations in an Asymmetric Vocal-Fold Model. Journal of the Acoustical Society of America, 97, 1874-1884. http://dx.doi.org/10.1121/1.412061
- 15. Mergell, P., Herzel, H. and Titze, I.R. (2000) Irregular Vocal-Fold Vibration—High-Speed Observation and Modeling. Journal of the Acoustical Society of America, 108, 2996-3002. http://dx.doi.org/10.1121/1.1314398
- 16. Eysholdt, U., Rosanowski, F. and Hoppe, U. (2003) Vocal Fold Vibration Irregularities Caused by Different Types of Laryngeal Asymmetry. European Archives of Oto-Rhino-Laryngology, 260, 412-417. http://dx.doi.org/10.1007/s00405-003-0606-y
- 17. Zhang, Y. and Jiang, J.J. (2004) Chaotic Vibrations of a Vocal Fold Model with a Unilateral Polyp. Journal of the Acoustical Society of America, 115, 1266-1269. http://dx.doi.org/10.1121/1.1648974
- 18. Schwarz, R., Hoppe, U., Schuster, M., Wurzbacher, T., Eysholdt, U. and Lohscheller, J. (2006) Classification of Unilateral Vocal Fold Paralysis by Endoscopic Digital High-Speed Recordings and Inversion of a Biome-chanical Model. IEEE Transactions on Biomedical Engineering, 53, 1099-1108. http://dx.doi.org/10.1109/TBME.2006.873396
- 19. Zhang, Z. (2010) Vibration in a Self-Oscillating Vocal Fold Model with Left-Right Asymmetry in Body-Layer Stiffness. Journal of the Acoustical Society of America, 128, EL279-EL285. http://dx.doi.org/10.1121/1.3492798
- 20. Mehta, D.D., Deliyski, D.D., Quatieri, T.F. and Hillman, R.E. (2011) Automated Measurement of Vocal Fold Vibratory Asymmetry from High-Speed Videoendoscopy Recordings. Journal of Speech, Language, and Hearing Research, 54, 47-54. http://dx.doi.org/10.1044/1092-4388(2010/10-0026)
- 21. Wurzbacher, T., Schwarz, R., Dollinger, M., Hoppe, U., Eysholdt, U. and Lohscheller, J. (2006) Model-Based Classification of Nonstationary Vocal Fold Vibrations. Journal of the Acoustical Society of America, 120, 1012-1027. http://dx.doi.org/10.1121/1.2211550
- 22. 张礼和, 程启明. 嘶音的三质量块声带模型分析法[J]. 中国生物医学工程学报, 1991, 10(4): 208-214.
- 23. Cveticanin, L. (1992) The Influence of the Reactive Force on a Nonlinear Oscillator with Variable Para-meter. Journal of Applied Mechanics, 114, 578-580.
- 24. Cveticanin, L. (1993) Approximate Solution of a Coupled Differential Equation with Variable Parameter. Journal of Applied Mechanics, 60, 214-217. http://dx.doi.org/10.1115/1.2900753
- 25. Cveticanin, L. (1995) Approximate Solution of a Time-Dependent Differential Equation. Meccanica, 30, 665-671. http://dx.doi.org/10.1007/BF00986572
- 26. 蔡莲红, 现代语音技术基础与应用[M]. 北京: 清华大学出版社, 2003.
- 27. J.P.H. van Santen. 语音合成[M]. 北京: 力学工业出版社, 2005.
- 28. 赵守国, 王素品, 孙义和. 声带振动功能模式识别的研究[J]. 西安交通大学学报, 2002, 12(36): 1258-1261.
- 29. Stepp, C.E., Hillman, R.E. and Heaton, J.T. (2010) A Virtual Trajectory Model Predicts Differences in Vocal Fold Kinematics in Individuals with Vocal Hyperfunction. Journal of the Acoustical Society of America, 127, 3166-3176.
- 30. 胡航. 语音信号处理[M]. 哈尔滨: 哈尔滨工业大学出版社, 2009.
- 31. 边肇祺, 张学工. 模式识别[M]. 北京: 清华大学出版社, 2000.
- 32. 万明习, 程敬之. 声门图信号起源及其与声带振动模式的关系[J]. 中国生物医学工程学报, 1992(2): 120-127.
- 33. Wurzbacher, T., Dollinger, M., Schwarz, R., Hoppe, U., Eysholdt, U. and Lohscheller, J. (2008) Spatiotemporal Classification of Vocal Fold Dynamics by a Multimass Model Comprising Time-Dependent Parameters. Journal of the Acoustical Society of America, 123, 2324-2334. http://dx.doi.org/10.1121/1.2835435