Computer Science and Application
Vol.06 No.09(2016), Article ID:18635,14
pages
10.12677/CSA.2016.69069
Research on K-Means Algorithm Analysis and Improvement
Chuanyu Zang, Yong Shen, Yuhao Zhang, Changgeng Chen, Hao Zhang, Zhendi Yang
School of Software, Yunnan University, Kunming Yunnan

Received: Sep. 7th, 2016; accepted: Sep. 22nd, 2016; published: Sep. 29th, 2016
Copyright © 2016 by authors and Hans Publishers Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/



ABSTRACT
Traditional k-means algorithm uses a random number to initialize the cluster center, the main advantage of this method is the ability to quickly produce cluster center initialization, its main drawback is initializing cluster centers may appear in the same a category, leading to excessive iterations, errors and even local optimum clustering result. For the shortcomings of traditional k-means algorithm initial cluster centers, this paper presents the pK-means algorithm, which uses a mathematical geometric distance method for improving the k-means clustering phenomenon of multiple algorithms initial cluster centers unevenly distributed Center appear in the same class cluster phenomenon, this approach avoids k-means clustering algorithm clustering process into local optimization, on the other hand reduces the clustering process repeated iterations. After analyzing and comparing two algorithm experimentally, the article found that the improved algorithm is better than the traditional k-means algorithm converges quickly, not easy to fall into local optimum.
Keywords:Machine Learning, Cluster Analysis, K-Means Algorithm, p-K-Means Algorithm

K-Means算法的研究分析及改进
藏传宇,沈勇,张宇昊,陈长庚,张浩,杨真谛
云南大学软件学院,云南 昆明

收稿日期:2016年9月7日;录用日期:2016年9月22日;发布日期:2016年9月29日

摘 要
传统的k-means算法采用的是随机数初始化聚类中心的方法,这种方法的主要优点是能够快速的产生初始化的聚类中心,其主要缺点是初始化的聚类中心可能会同时出现在同一个类别中,导致迭代次数过多,甚至陷入局部最优出现错误的聚类结果。针对传统的k-means算法初始聚类中心的缺点,本文提出了p-K-means算法,该算法采用了数学几何距离的方法改进k-means算法中初始聚类中心分布不均匀的现象多个聚类中心出现在同一类簇中的现象,这种方法能避免k-means聚类算法聚类过程中陷入局部最优,另一方面降低了聚类过程中的反复迭代次数。本文通过实验的方式来对两个算法进行分析比较后发现改进的算法在收敛速度上优于传统k-means算法,也不容易陷入局部最优。
关键词 :机器学习,聚类分析,K-Means算法,p-K-means算法

1. 引言
随着当今社会的经济发展,计算机技术也逐渐进入了一个新兴的时代。数据的大量增加,信息量的急剧膨胀,云计算和大数据时代就在这样的环境中应运而生。云计算是一种以互联网为基础的计算方式,并且以这样的方式将软硬件资源和信息提供给有需求的计算机或其他设备。大数据是在云计算的基础平台上进行数据的存储和数据中潜在知识的挖掘处理 [1] 。
大数据已经渗透到了人们生活中的各个方面,包括金融行业,医学行业,管理行业,其中以信息IT行业最为明显,数据的聚类分析是大的数据分析工具最常用的分析方法,聚类分析:是通过数据对象的某一属性或多个属性将其进行分类。或根据各个样品(individuals, objects or subjects)将其分类来表征,使得相同类别中的各个具有最高可能的同质性(homogeneity),和类别之间应具有尽可能高的异质性(heterogeneity)。为了获得更合理的分类,首先使用的适当指标来定量描述研究对象(样品或变量,常用样品)的程度之间的密切联系。常用“距离”和“相似性因子”的指标来衡量。在聚类分析,一般的规则是在同一类别的“距离”更小点或“相似系数”较大的点划归为一个簇,“距离”较大点或“相似系数”的小点返回了不同来的类簇 [2] 。
本文主要研究的是k-means算法的研究分析及改进,首先简介了k-means算法理论及缺点,并提出了p-K-means算法,该算法采用了数学几何距离的方法改进k-means算法中初始聚类中心分布不均匀的现象多个聚类中心出现在同一类簇中的现象,这种方法能避免k-means聚类算法聚类过程中陷入局部最优,另一方面降低了聚类过程中的反复迭代次数。通过实验验证了改进算法的有效性。
2. 传统K-means算法概述
2.1. 聚类分析
聚类分析(Cluster Analysis),也被称为集群分析,基于生活中“物以类聚”的道理,是对于某个样品或指标进行分类多元统计分析方法,它需要一组单独的属性或特性的代表变量,称为聚类变量。根据个人的样品或松紧之间的联系进行分类。一般分类变量的组合是由研究者指定的,不是这样的估计推断其他多元分析方法 [3] 。
聚类方法要求 [4] :
(1) 聚类分析需要简单,便于人直观理解。
(2) 聚类分析主要是对未知事物的类别相似性探索,可能会有多个分析结果。
(3) 聚类分析一般情况必需是收敛的,无论现实中是否存在都能得出客观的解。
(4) 聚类分析的聚类属性选择是客观的,可以选择其中几个属性,也可以选择多个属性。
(5) 聚类分析的解完全依赖于研究者所选择的聚类变量,增加或删除一些变量对最终的解都可能产生实质性的影响。
2.2. K-means算法
K-means聚类(K-均值聚类)算法是要确定类的数目k为聚类数据集的一个先决条件,通常是簇的数目被事先确定,K-means聚类算法是算法的最广泛使用的算法之一,对于大型数据处理效率比较高,特别是当样本分布呈现更明显的团聚现象时效果会更好 [5] 。
K均值算法的基本思想是给定的随机初始k个簇中心,按照训练数据的最近点的原则进行分类分配给每个群集。然后根据平均的方法来计算每个群集的质心,从而确定新的集群簇心。一直迭代,直到簇心的移动距离小于某个给定的值后结束算法 [6] 。
2.3. K-means算法思想
K-means算法的基本思想是:首先指定需要划分簇的k值的大小;然后采用随机数生成随机选择K个初始数据对象来初始化聚类中;然后计算集合中其他数据对象到各个聚类中心的几何距离(不一定是欧氏距离),将各个数据对象计算的距离后将其划归为距离该对象最近的聚类中心点,采用物理上计算重心的方法调整聚类中心(将聚类中心移动至中心位置),计算完成后看算法是否收敛,如果没有收敛,反复迭代执行,迭代后需要比较两次聚类中心移动的位置,如果移动位置小于某个值或者未移动表明算法收敛。当所有聚类中心都收敛表示算法以及结束 [7] 。
经典K-means算法的基本工作流程:首先随机选取K个数据作为的聚类的聚类中心,计算各个数据对象到所选出来的各个中心的距离,将数据对象指派到最近的簇中;然后计算每个簇的均值,循环往复执行,直到满足聚类的收敛条件为止。图1显示了k-means算法的执行步骤 [8] 。
具体的执行步骤如下:
输入:用户需要输入分类簇的数目K以及包含n个数据对象的数据集合。
输出:k个聚类完成的簇
步骤1:在输入的数据对象集合中随机初始化k个点作为k-means算法样本;
步骤2:计算给定的数据集合分别到初始化聚类中心的几何距离
步骤3:按照距离最短原则将没一点数据分配到最邻近的簇中
步骤4:使用每个簇中的样本数据几何中心作为新分类的聚类中心;
步骤5:反复迭代算法中步骤2、步骤3和步骤4直到算法收敛为止
步骤6:算法结束,得到输出结果。
2.4. K-means算法的分析
K-means算法是一种基于划分的聚类算法,在给定的数据集中找出一种划分方案使得规定的误差达到最小的k个分类,当簇与簇之间的特征比较明显时,并且结果簇比较密集时,K-means算法的效果比较好。K-means聚类算法的优点主要集中在:算法快速、简单;对大数据集有较高的运行效率并且是可
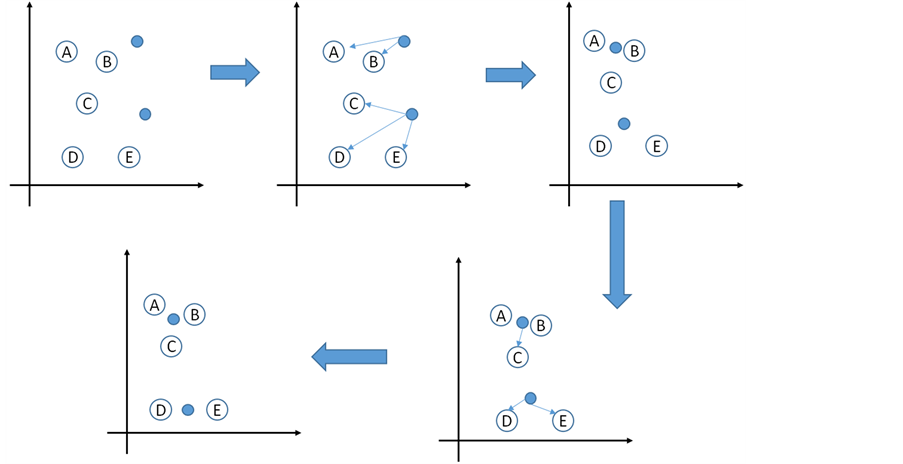
Figure 1. K-means algorithm steps
图1. K-means算法步骤
伸缩性的;时间复杂度接近于O(n),适合比较大规模的数据聚类。但是另一方面K-means算法也存在很多缺点:
(1) K-means聚类算法用户需要对其进行聚类数目的指定,即k值的指定。
(2) K-means算法对初始的聚类中心依赖性很大,容易陷入局部最优。
(3) 噪声数据对K-means算法的影响比较大。
3. K-means算法改进(p-K-means)
3.1. K-means算法改进综述
K-means算法是比较经典的算法,也是应用比较广泛的数据挖掘算法之一,其拥有比较强的局部搜索能力,能适应大数据集的聚类要求,容易理解和实现。但是K-means聚类算法存在一定的局部性:首先k值需要用户事先指定,用户对k值的估计比较困难;其次K-means最大的缺点是对初始化的聚类中心位置依赖性比较大,容易造成算法迭代次数增加和陷入局部最优的情景。因此如果能初始化比较好的聚类中心能使K-means算法快速收敛和找到全局最优。本文针对K-means中初始聚类中心缺陷提出了p-K-means算法,该算法基于角度的计算来实现初始化聚类中心。
3.2. 相关定义
经过对传统k-means算法的缺点的分析后本文提出了p-K-means算法,为了更好的描述p-K-means算法,本文做了如下定义:
定义3:令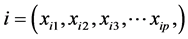 和
和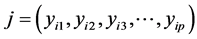 分别是两个不同的数据对象,它们的维度都是p维,则定义它们的几何距离为:
分别是两个不同的数据对象,它们的维度都是p维,则定义它们的几何距离为:
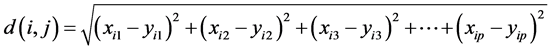
定义4:令数据对象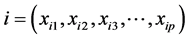 (i的维度为p维)到集合U(U为样本点的集合)几何距离为:
(i的维度为p维)到集合U(U为样本点的集合)几何距离为:
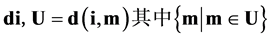
定义5:对于集合中的数据对象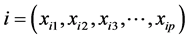 和数据对象
和数据对象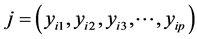 ,假设数据对象m到两个数据对象i和j的聚类同时达到最远则满足如下条件:
,假设数据对象m到两个数据对象i和j的聚类同时达到最远则满足如下条件:
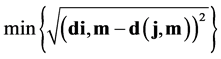
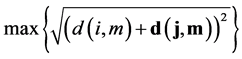
定义6:集合U中的算术平均数计算方式如下所示:
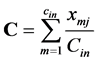
3.3. p-K-means算法思想
本文在针对K-means算法初始化聚类中心不正确而出现了聚类陷入了局部最优甚至是错误的聚类结果的现象,前人提出的最大距离的选择聚类中心的思想,该算法主要的目的是避免初始化的聚类中心出现在同一簇的点集中。
本文参考了“最大距离选择聚类中心”的算法思想,提出了p-K-means聚类算法。该算法基于数学上的角度的变化和最大距离的方法来实现,p-K-means算法具体步骤为(图2):
步骤1:输入聚类数据data和数据和聚类数目K
步骤2:计算两两数据对象之间的距离,找到最大的距离d和两个几何距离最大的连个点C1和C2。
步骤3:将所有点从集合中虚拟删除(不参与下一次的查找增加标志位)。
步骤4:以C1和C1为初始的基础聚类中心,从集合中搜索C3使得C3到C1和C2距离同时最大(即C3满足定义3中的条件)。
步骤5:比较判断聚类中心的数目是否等于输入的k值,如果小于K则重复步骤3和步骤4 (直到聚类中心的数目等于k值为止),当聚类中心的数目等于K值时,进行下面步骤计算。
步骤6:计算所有点到聚类中心距离,找到点的最近的聚类簇。
步骤7:计算每一个聚类簇的重心,移动聚类中心。
步骤8:如果算法不收敛则重复计算步骤5和步骤6,如果算法收敛则结束算法。
从p-K-means聚类算法的基本8个计算步骤中可以看出:p-K-means聚类算法的聚类中心并不是跟传统K-means算法一样随机选取,是通过数学几何计算计算之后产生的聚类中心,一方面使得初始的聚类中心尽可能分散在距离各个聚类簇更近,另一方面尽可能的选择初始聚类中心尽可能分散开,与原来的K-means算法比起来,初始化聚类算法聚类中心更能体现数据样本的分布,这样就使得K-means算法不至于陷入局部最小。图3是p-K-means算法中选取的聚类中心的主要步骤:
p-K-means选取初始聚类中心主要步骤:
步骤1:从集合U中选取两两数据对象,分别计算两两数据对象之间的距离,将其距离存储到领阶矩阵D中和两个点C1和C2;
步骤2:从矩阵D中找出距离最大的两个点C1和C2,其最大距离记为max inD,将两个最大的点C1和C2作为初始的两个聚类中心。
步骤3:利用p-K-means选取初始聚类中心的思想选取聚类中心:将步骤2中求出的C1和C2加入初始聚类中心集合center中最为初始聚类中心;在集合U中虚拟删除(加上标志位)找到的两个聚类中心

Figure 2. P-K-means algorithm process
图2. P-K-means算法流程
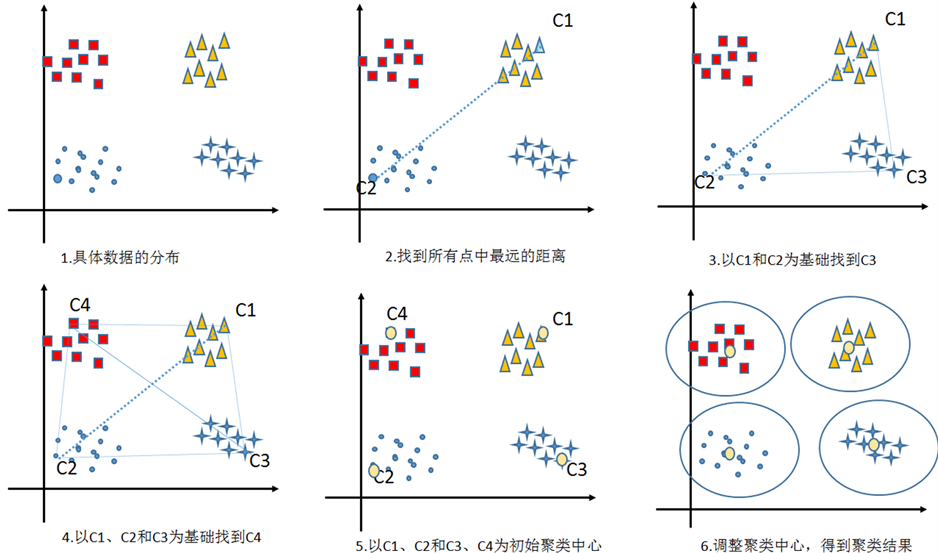
Figure 3. P-K-means clustering center select key steps
图3. P-K-means聚类中心选取主要步骤
C1和C2。以center集合中的点为参照点,在U查找,找到C3点,使得C3点到C1和C2点的几何距离同时满足最大,即满足条件
{
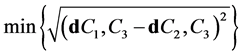
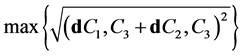
};
判断center集合的聚类中心的个数是否等于k,如果不等于,继续寻找k个初始的聚类中心。
3.4. p-K-means算法实现
通过对K-means算法的分析后可以看出K-means算法存在很多缺点,本文提出的p-K-means主要从聚类中心的选取方面来对K-means算法进行优化:采用数学上的几何距离和集合的思想对K-means算法进行改进。
算法p-K-means
输入:聚类数据D,聚类簇个数k。
输出:k个聚类簇。
具体代码如下所示(此处仅包含p-K-means算法聚类中心选取步骤的主要代码):
该算法通过优化k-means中的初始聚类中心的选取办法,采用数学上的几何距离和集合的思想对K-means算法进行改进使得初级聚类中心尽可能的分散。
3.5. p-K-means算法实例
为了能更好的说明p-K-means算法中关于聚类中心的初始化过程,下面将具体举例说明,如图4所示,为了方便数据的可视化,本节将采用二维平面的数据,列举了10个样本点为示例集合:
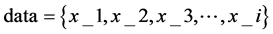 (假设数据已经经过清洗,噪声数据已经没有了) p-K-means的具体步骤为:
(假设数据已经经过清洗,噪声数据已经没有了) p-K-means的具体步骤为:
假设我们需要将这10个点分成3个簇,即我们需要输入的k = 3;
(1) 计算样本点集合data中的这10个点之间的欧式距离,找出距离最远的两个点分别是x1和x10,将x1和x10从整个集合中虚拟删除,不参与下一次的聚类中心的查找。
(2) 计算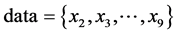 到点x1和x10的集合距离,分别存储于邻接矩阵X1和X10中。
到点x1和x10的集合距离,分别存储于邻接矩阵X1和X10中。
(3) 从X1和X10中找到一个点满足定义5 (即找到一个点到两点x1和x10的几何距离同时最大)。该实例中找到点X9。
(4) 重复步骤(2)和步骤(3)。
(5) 判断聚类中心数目是否满足等于k。
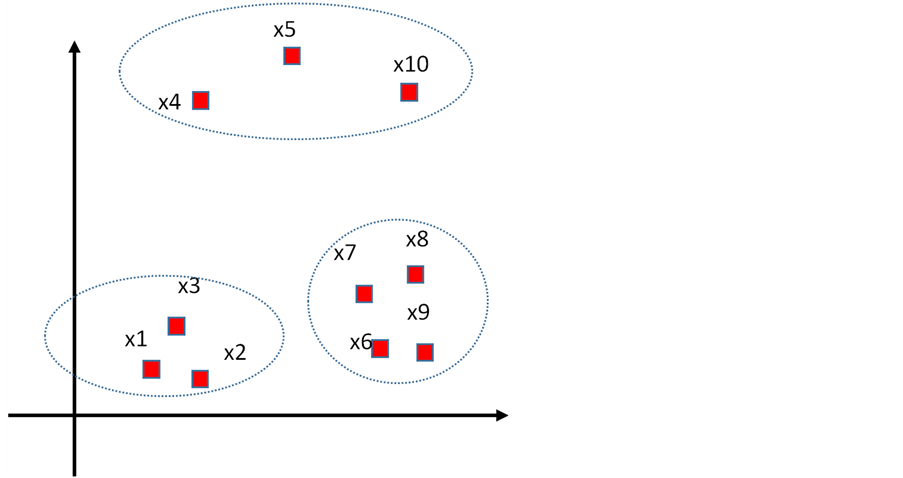
Figure 4. P-K-means clustering center selection example
图4. P-K-means聚类中心选择举例
3.6. p-K-means算法缺陷
虽然p-K-means算法解决了K-means对初始化聚类中心的依赖缺点,使得聚类算法聚类迭代次数得到了降低,另一方面p-K-means使得聚类不会有陷入局部最优的情况出现,但是p-K-means需要首先在聚类之前找到距离最远的两个聚类中心,这个算法的时间复杂度是O(n^2),使得算法的时间复杂度有所提高,也是p-K-means的一个最大的缺点。此外p-K-means算法容易受到噪声点的影响。
4. 实验分析
4.1. 实验环境说明
本文首先通过对传统K-means和改进后的p-K-means进行理论分析,显然在理论上改进后的p-K-means算法更不容易陷入局部最优,理论上也能减少数据的迭代次数。下面将通过具体实验来验证算法在改进前后的结果比较。
本文实验过程采用python语言分别来实现K-means算法和改进前后的p-K-means算法。在相同的试验环境下对两种算法的运行效率和运行结果进行了分析和对比。具体的实验环境如表1所示。
为了能直观的展示数据聚类的整个过程,本次试验中采用了100个二维平面点来进行实验分析(该数据由网上下载),数据具有随机性(为了不失一般性),具体的数据分布如图5所示。
4.2. K-means算法实验分析
K-means算法初始化聚类中心采用的是随机选取数据中的点,因为K-means算法对初始化聚类中心依赖性比较大,很可能陷入局部最优的情况,另一方面这种方式使得迭代次数增加。
如图6所示,实验中K-means算法的整个聚类过程,图中每一种颜色表示一个聚类簇,圆点表示聚类样本,红色正方形表示聚类中心。
从图中可以看出,初始化导致第一次聚类的过程中两个类别的初始聚类中心初始化在了同一个类别中,导致迭代次数过多,甚至有时候会出现局部最优导致错误的聚类,这也是k-means算法中比较大的缺点。
4.3. p-K-means算法实验分析
p-K-means是本文通过对K-means算法进行研究和分析后发现K-means算法存在对初始聚类依赖性较大的缺点,采用数学上的方法将聚类中心尽可能的分散在整个数据集合上,避免了K-means陷入局部最小,另一方面也是降低了k-means算法的迭代次数。收敛速度也得到了提升。图7是p-K-means算法的聚类过程。
Table1. Lab environment
表1. 实验环境
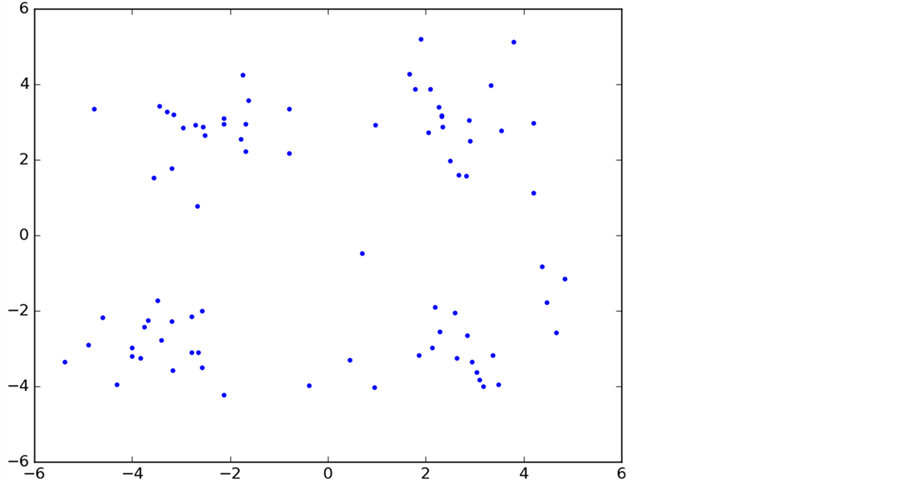
Figure 5. Test data distribution
图5. 测试数据分布图
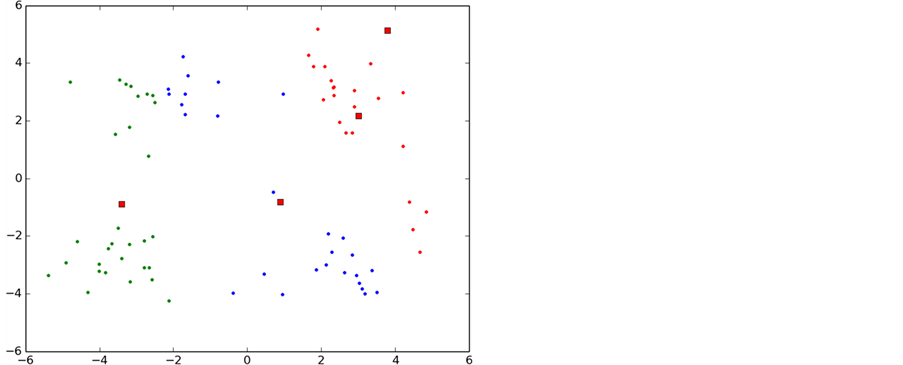
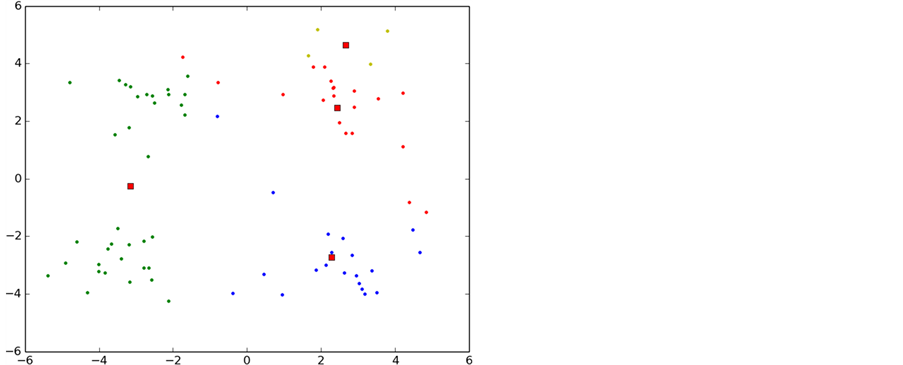

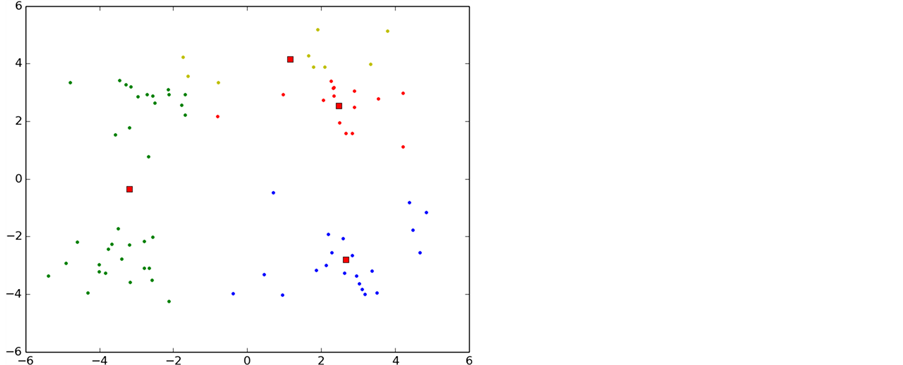
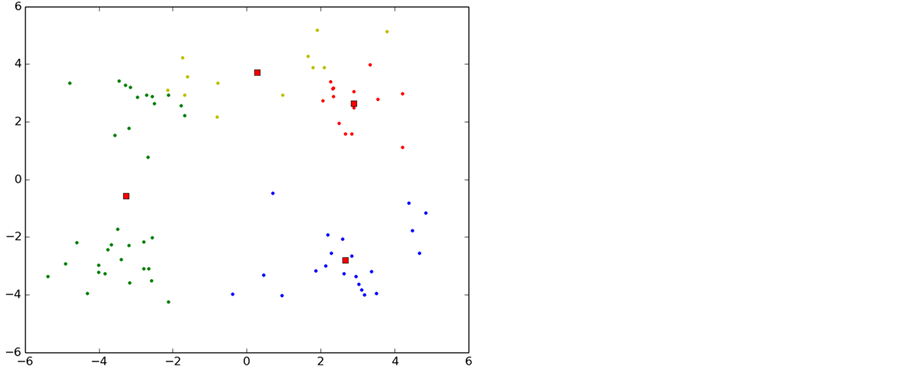
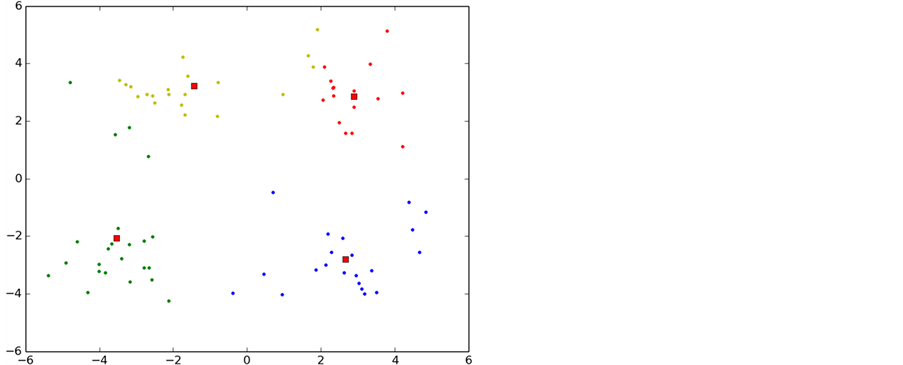
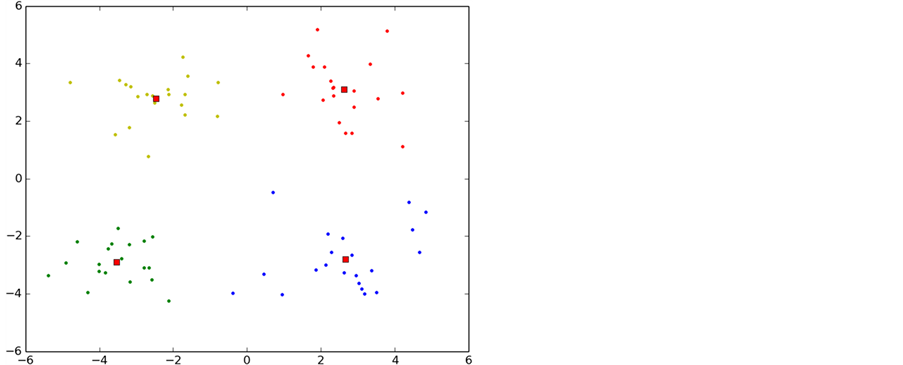
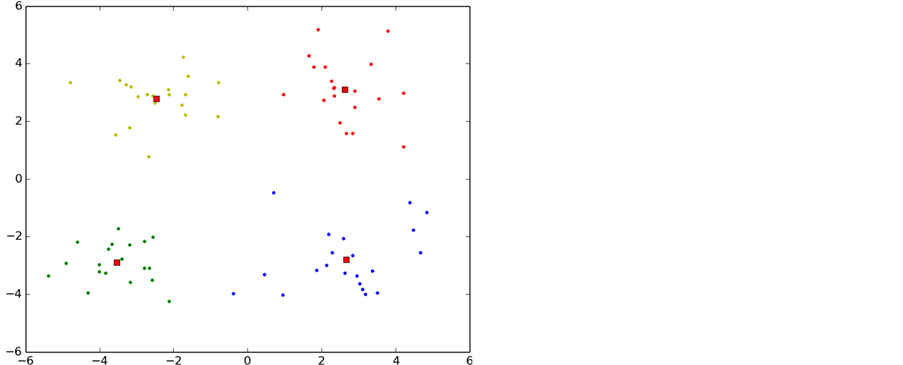
Figure 6. K-means clustering algorithm
图6. K-means算法聚类过程
通过p-K-means的初始化合理的聚类中心发现只经过3次迭代就已经收敛,另一方面可看出p-K-means算法能有效的避免K-means算法陷入局部最优的情况。
4.4. p-K-means算法与K-means算法比较
p-K-means算法是本文提出的对K-means的一种改进方案,p-K-means算法初始化聚类中心时使聚类
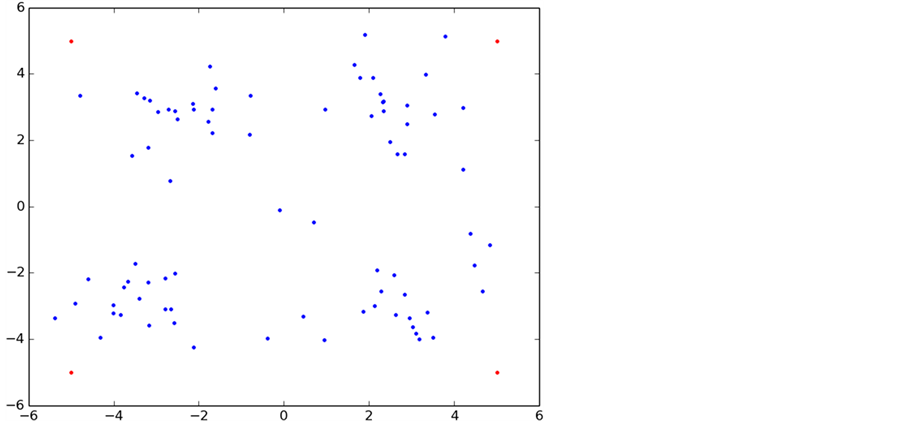
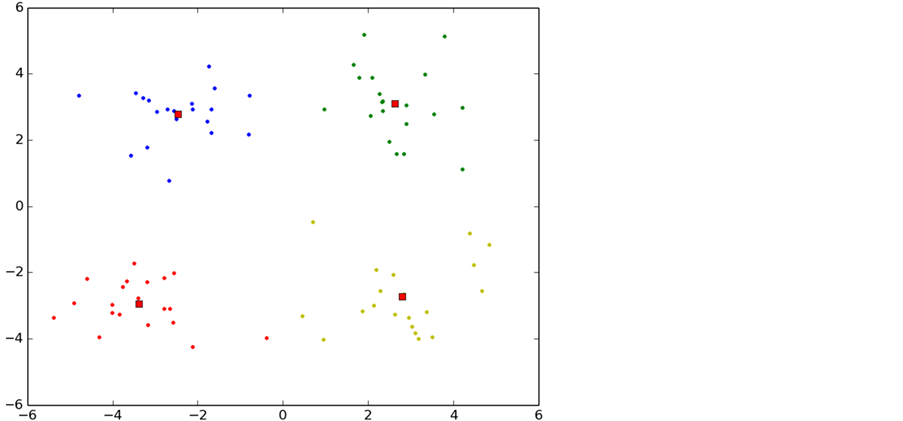
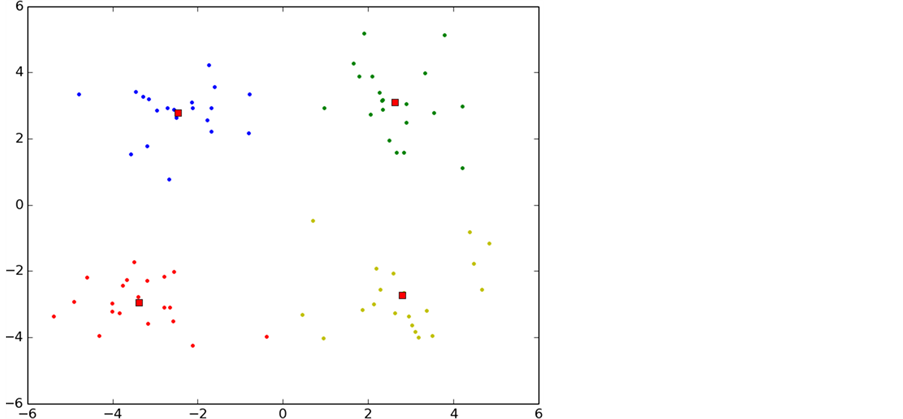
Figure 7. P-K-means clustering algorithm
图7. P-K-means算法聚类过程
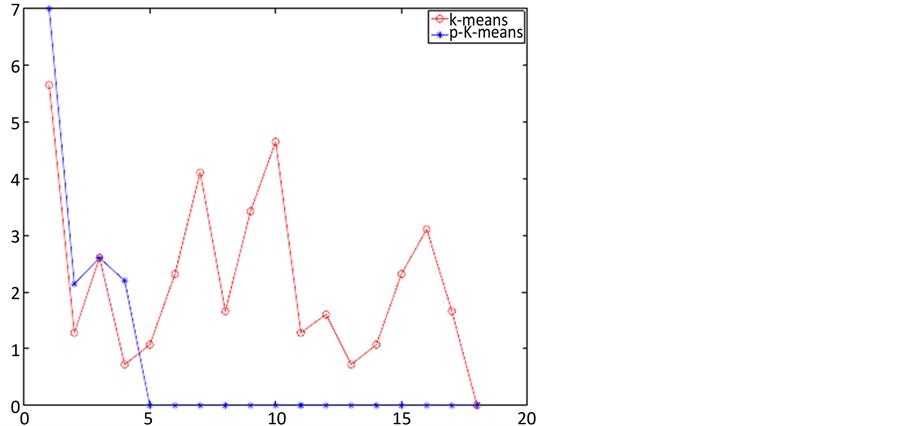
Figure 8. Comparison of p-K-means and K-means algorithm convergence process
图8. P-K-means与K-means算法收敛过程的比较
中心尽可能的保持远距离,避免多个聚类中心出现在同一个类中,该思想也是参考了前人的“最大距离思想”,但是p-K-means算法能保证所有初始化聚类中心均匀的分散在这个数据集中,避免了聚类中出现局部最优的情况。收敛次数也相应的减少,如图8是p-K-means与K-means算法的收敛过程:
如图8所示,红色曲线表示K-means算法的收敛过程,蓝色曲线表示平p-K-means算法的收敛情况,同样的数据p-K-means算法仅仅用了5次就收敛,而K-means算法用了18次才收敛。
5. 总结与展望
本文的主要成果是对机器学习主要思想进行了阐述,进一步分析了聚类算法中比较有代表性的k-means算法,分析后发现k-means算法存在对初始聚类中心依赖较大的缺陷,因为传统的k-means算法采用的是随机初始化聚类中心的方法,导致聚类过程中会出现局部最优的现象,有可能导致聚类结果错误。
本文经过理论分析和实验分析后提出了一种对传统k-means算法改进的方案提出了p-K-means算法,通过合理的方式初始化K-means算法聚类中心,本文还通过实验对比了传统的K-means算法和改进后的p-K-means算法做了对比。分析了改进算法p-K-means存在的缺陷。
本文虽然对经典算法有了一定效率上的改进,但是仍然存在很多课改进的问题,例如,本文阐述的算法是在单线程的中完成的,实际上该算法相互之间的耦合度不太高,相信在以后会通过相应的算法将其数据集进行解耦之后运行在多线程环境中,并且在理论上是可以实现分布式计算模式的,所以分布式k-means算法相信会有更高的效率。
基金项目
云南省软件工程重点实验室开放基金项目:模式驱动服务组合研究(2012SE306)。云南省软件工程重点实验室开放基金项目:基于云计算环境的服务组合涌现研究(2015SE204)。
文章引用
藏传宇,沈勇,张宇昊,陈长庚,张浩,杨真谛. K-Means算法的研究分析及改进
Research on K-Means Algorithm Analysis and Improvement[J]. 计算机科学与应用, 2016, 06(09): 551-564. http://dx.doi.org/10.12677/CSA.2016.69069
参考文献 (References)
- 1. 哈林顿. 机器学习实战[M]. 北京: 人民邮电出版社, 2013.
- 2. 于孝美. 基于半监督学习的算法研究改进[D]: [硕士学位论文]. 济南: 济南大学, 2013.
- 3. 李卫军. K-means聚类算法的研究综述[J]. 现代计算机(专业版), 2014(8): 85-89.
- 4. 黄静. 基于改进K-means算法的蚕茧自动计数方法的研究[J]. 丝绸, 2014(3): 35-41.
- 5. 崔丹丹. K-means聚类算法的研究与改进[D]: [硕士学位论文]. 合肥: 安徽大学, 2012.
- 6. 周鑫. K-means算法的研究与改进[J]. 微计算机信息, 2008(10): 31-33.
- 7. 施瓦茨. 深入理解机器学习[M]. 北京: 机械工业出版社, 2016.
- 8. 埃塞姆. 机器学习导论[M]. 北京: 机械工业出版社, 2016.