Journal of Water Resources Research
Vol.06 No.05(2017), Article ID:21928,9
pages
10.12677/JWRR.2017.65054
Flood Coincidence Probability Analysis for Mainstream and Tributaries of the Jialing River Basin Based on Copula Function
Qixiang Ran, Chang Peng, Xuan Ling
Hydrology and Water Resources Survey Bureau of Upper Yangtze River, Bureau of Hydrology, CWRC, Chongqing

Received: Aug. 15th, 2017; accepted: Aug. 26th, 2017; published: Sep. 5th, 2017

ABSTRACT
Flood coincidence probability is a multivariable hydrologic event. At present, the research is mostly limited to the statistical analysis of observed data. In this study, the annual maximum flood peak data of four hydrological stations in Jialing River and its tributaries, including the Beibei, Xiaoheba, Luoduxi and Wusheng station, are selected for case study. The bivariate copula functions are introduced and used to construct the joint distributions of flood peak. The design flood and flood coincidence probability are computed for different return periods. The result shows that the flood coincidence probability of high return periods is smaller than low return periods. The flood coincidence probability of Jialing River and its tributaries in the same return periods, Qujiang River is greater than Jialing River, and Fujiang River is among the smallest. This study will provide a new approach for Flood encounter analysis.
Keywords:Jialing River Basin, Flood Coincidence Probability, Copula Function, Multivariable
基于Copula函数的嘉陵江流域干支流 洪水遭遇分析
冉啟香,彭畅,凌旋
长江水利委员会水文局长江上游水文水资源勘测局,重庆

收稿日期:2017年8月15日;录用日期:2017年8月26日;发布日期:2017年9月5日

摘 要
洪水遭遇是一个多变量水文事件,目前研究多限于对实测资料进行统计分析。基于二维copula函数分别建立嘉陵江干流北碚站与支流小河坝站、罗渡溪站、武胜站洪峰流量的联合分布。计算各站不同重现期的设计洪水,推求出对应的洪水遭遇概率。结果表明,嘉陵江流域低重现期洪水遭遇概率大于高重现期;同一重现期下,嘉陵江各支流与干流(北碚站)的洪水遭遇概率,渠江大于嘉陵江,涪江最低。此方法为计算洪水遭遇分析计算提供了一条新途径。
关键词 :嘉陵江流域,洪水遭遇,Copula函数,多变量

Copyright © 2017 by authors and Hans Publishers Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/


1. 引言
研究流域的洪水遭遇问题,为防洪减灾及设计洪水提供了重要的意义。目前常见方法是对水文站历年同步资料进行统计分析,如范可旭等统计了乌江和长江三峡洪水遭遇的概率 [1] ;熊莹根据实测资料,分析了金沙江与岷江、长江与嘉陵江、长江与乌江的洪水遭遇 [2] ;张洪刚等进行了长江流域洪水地区组成与遭遇规律研究 [3] 。但统计方法只能对实测洪水资料进行分析,无法定量估计发生百年一遇或千年一遇设计洪水的遭遇频率。在水文事件中,洪水遭遇分析往往不是单一变量的,流域的干支流洪水之间存在着一定的相依关系,洪水遭遇是一个多变量的频率组合问题。
目前常见的多变量水文分析方法主要有基于正态变换的Moran法、将多维转化为一维的费永法、传统经验频率法、非参数法以及Copula函数法等 [4] ,各方法都有优缺点,其应用范围和适用条件也不同。Copula函数的优点在于不需要假设变量是独立的或者正态分布的或者它们具有相同的边缘分布,它可以用来描述水文变量之间的相关性结构,能够灵活的构造边缘分布为任意分布的水文变量联合分布。近年来,采用Copula函数法进行洪水遭遇分析已成为一个研究热点,陈璐等基于多维Copula函数构建金沙江屏山站、岷江高场站、嘉陵江北碚站以及长江宜昌站的洪水发生时间和量级的联合分布 [5] ;闫宝伟等应用Copula函数构建了长江和清江年最大洪水发生时间及发生时间与量级之间的联合分布,得到两江洪水遭遇的风险率 [6] ;关帅等基于Copula函数进行了韩江流域干支流洪水遭遇计算 [7] ,李天元等建立了基于copula函数的非连续序列洪水频率分析模型,进行非连续序列洪水频率分析 [8] 。
嘉陵江流域位于长江上游,是长江流域面积最大的支流,也是长江洪水的主要来源之一。嘉陵江流域内水系主要由渠江、涪江和嘉陵江组成,渠江和涪江分别从左、右岸在重庆合川区汇入嘉陵江。目前关于嘉陵江流域内洪水遭遇的分析研究还较少,苗磊 [9] 在对西汉水和嘉陵江干流典型历史洪水调查的基础上,分析了西汉水与嘉陵江干流洪水遭遇情况,但嘉陵江下游渠江、涪江以及嘉陵江干流的洪水遭遇研究尚未开展。根据历史资料,嘉陵江平均每4年就会发生一次洪水,由于不同的暴雨时空分布和走向、干支流洪水组成及遭遇情况各异,致使嘉陵江下游洪水过程多呈双峰或多峰形,洪水频发对流域内的人民生命和财产安全造成了较大的威胁。因此,本文研究面向嘉陵江流域内洪水遭遇分析的迫切需求,基于小河坝、武胜、罗渡溪以及北碚水文站点长系列资料,利用copula连接函数,构建嘉陵江干支流年最大洪峰流量的二维联合分布,分析嘉陵江流域内干支流洪水遭遇的规律,为嘉陵江流域的防灾减灾提供理论参考和决策依据。
2. Copula函数简述
Copula函数是定义域为 均匀分布的多维联合分布函数,它可以将多个变量的边缘分布连接起来构造联合分布,它的表述如下:
均匀分布的多维联合分布函数,它可以将多个变量的边缘分布连接起来构造联合分布,它的表述如下:
 (1)
(1)
式中: 为
为 的边缘分布,
的边缘分布, 为随机变量的个数,
为随机变量的个数,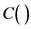 为Copula函数。
为Copula函数。
目前水文领域里常用的是Archimedean Copula函数,Archimedean型又分为对称型和非对称型两种形式。本文介绍二维Archimedean Copula函数,二维Archimedean Copula函数是对称的。
1) Gumbel Copula函数。
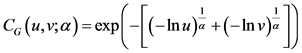 (2)
(2)
Gumbel Copula函数的相关参数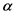 与传统的相关性和一致性测度常有一一对应的关系,Kendall秩相关系数
与传统的相关性和一致性测度常有一一对应的关系,Kendall秩相关系数 与
与 的关系为
的关系为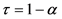 。
。
2) Clayton Copula函数。
 (3)
(3)
Clayton Copula函数的相关参数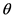 与Kendall秩相关系数
与Kendall秩相关系数 的关系为
的关系为 。
。
3) Frank Copula函数。
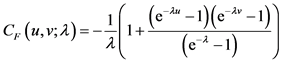 (4)
(4)
Frank Copula函数的相关参数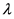 与Kendall秩相关系数
与Kendall秩相关系数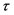 的关系为
的关系为 。其中
。其中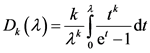 ,式中,
,式中,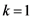 。函数
。函数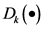 被称为“Debye”函数。
被称为“Debye”函数。
3. 流域概况
嘉陵江是长江上游左岸的主要支流,流经陕西、甘肃、四川、重庆四省,干流全长1120 km,落差2300 m,平均比降2.05‰。全流域面积15.98万km2,占长江流域面积的9%。渠江、涪江为嘉陵江流域的较大左、右支流,在合川城区汇入嘉陵江。武胜、北碚水文站分别为渠江和涪江汇入前、后的嘉陵江干流控制站,小河坝水文站为涪江的最下游控制站,罗渡溪水文站为渠江的最下游控制水文站。嘉陵江流域水系及站点分布见图1。
4. 实例研究
4.1. 数据选择
本文选择嘉陵江流域小河坝、武胜、罗渡溪、北碚站实测资料进行洪水遭遇计算,根据小河坝站1951~2014年、武胜站1944~2014年、罗渡溪站1953~2014年以及北碚站1939~2014年实测洪峰流量资料,按年最大取样,得到各站年最大洪峰流量序列。

Figure 1. Jialing River basin and hydrological station locations
图1. 嘉陵江流域水系及水文站分布图
4.2. 边缘分布
对于单变量水文系列资料,我国常采用P-III型分布,《水利水电工程设计洪水计算规范》中也推荐采用P-III型分布来计算设计洪水。边缘分布的经验频率计算公式:
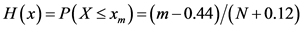 (5)
(5)
式中: 为
为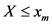 的频率,
的频率,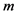 为
为 的序号,
的序号,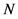 为样本容量。
为样本容量。
本文采用K-S以及均方根误差(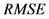 )来衡量边缘分布。
)来衡量边缘分布。 的计算公式为:
的计算公式为:
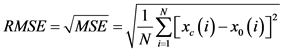 (6)
(6)
式中: 为均方差,
为均方差,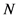 为样本容量,
为样本容量,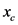 为理论频率,
为理论频率, 为经验频率,
为经验频率, 为样本序号。
为样本序号。
本文选用P-III型分布来构建各站年最大洪峰流量的边缘分布,并利用线性矩法进行参数估计,嘉陵江流域各站年最大洪峰流量的P-III型分布拟合情况见图2。用 和K-S对边缘分布进行检验,检验结果见表1。从表1可以看出,四站边缘分布的理论频率和经验频率的均方根误差(
和K-S对边缘分布进行检验,检验结果见表1。从表1可以看出,四站边缘分布的理论频率和经验频率的均方根误差( ),各站误差均较小;在5%的显著性水平下,K-S检验接受域为小于等于临界值0.173,四站的P-III型分布均通过了K-S检验。可以采用P-III型分布来构建边缘分布。
),各站误差均较小;在5%的显著性水平下,K-S检验接受域为小于等于临界值0.173,四站的P-III型分布均通过了K-S检验。可以采用P-III型分布来构建边缘分布。
4.3. 联合分布
采用二维Copula函数来描述两站之间的相关关系时,Copula函数的参数估计是构建二维联合分布的关键,Archimedean Copula函数联合分布的联结参数多采用Kendall秩相关系数 [10] 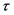 来得到,
来得到,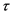 的计算公式为
的计算公式为
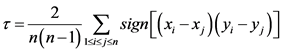 (7)
(7)
 (a) 小河坝站(Xiaoheba station) (b) 武胜站(Wusheng station)
(a) 小河坝站(Xiaoheba station) (b) 武胜站(Wusheng station)
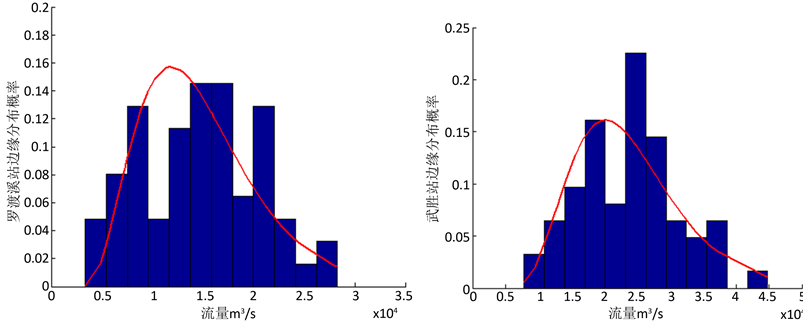 (c) 罗渡溪站(Luoduxi station) (d) 北碚站(Beibei station)
(c) 罗渡溪站(Luoduxi station) (d) 北碚站(Beibei station)
Figure 2. Fitting-figures of the marginal distributions
图2. 各站边缘分布拟合图
Table 1. Parameters and hypothesis test results of the marginal distributions
表1. 边缘分布参数及检验结果
式中,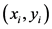 为样本,
为样本, 为样本个数,
为样本个数,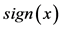 为符号函数。
为符号函数。
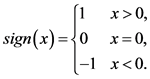
采用AIC最小准则 [11] 以及均方根误差来评价确定出最优的Copula函数。AIC最小准则是由日本学者赤池弘次在研究信息论问题时提出的,AIC值的表达式为:
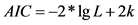 (8)
(8)
式中: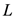 为极大似然函数,
为极大似然函数, 为独立参数的个数。
为独立参数的个数。
在水文计算中,一般常用的Copula函数是Archimedean Copula函数,本文选择Gumbel、Clayton以及Frank 3种常见的Copula函数进行比较分析,从中选择出最优的Copula函数来构建二维联合分布。嘉陵江流域狭长且分散,嘉陵江中上游、渠江和涪江之间的暴雨遭遇机会不大,本文计算嘉陵江流域干支流的洪水遭遇概率,因此联合分布分别为小河坝与北碚、武胜与北碚、罗渡溪与北碚二维Copula联合分布,Copula联合分布的参数及检验结果见表2。
由表2可知,三个联合分布中,罗渡溪与北碚的Kendall相关系数最大,说明两者关系密切,相关性较好。整体来看,Frank Copula函数的RMSE和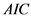 最大,Gumbel Copula函数的最小。小河坝与北碚的Gumbel Copula和Clayton Copula联合分布的RMSE和
最大,Gumbel Copula函数的最小。小河坝与北碚的Gumbel Copula和Clayton Copula联合分布的RMSE和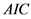 相差不大,但考虑年最大洪峰流量属于极值条件,需要采用能够描述上尾相关性的Copula函数,因此本文选择Gumbel Copula函数参与计算。干流北碚站与支流小河坝、罗渡溪、武胜站的Gumbel Copula联合分布的经验与理论点据曲线见图3,可知拟合效果较好。
相差不大,但考虑年最大洪峰流量属于极值条件,需要采用能够描述上尾相关性的Copula函数,因此本文选择Gumbel Copula函数参与计算。干流北碚站与支流小河坝、罗渡溪、武胜站的Gumbel Copula联合分布的经验与理论点据曲线见图3,可知拟合效果较好。
4.4. 联合分布重现期
重现期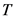 与累计频率
与累计频率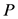 之间的关系为:
之间的关系为: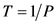 。对于水文多变量来说,重现期分为联合重现期和同现重现期 [7] ,联合重现期是指多个变量中至少有一个超过某一特定值时,事件发生的重现期;同现重现期是指多个变
。对于水文多变量来说,重现期分为联合重现期和同现重现期 [7] ,联合重现期是指多个变量中至少有一个超过某一特定值时,事件发生的重现期;同现重现期是指多个变
Table 2. Parameters and fitting inspection values of the Copula joint distributions
表2. Copula联合分布函数的参数估计值及拟合检验
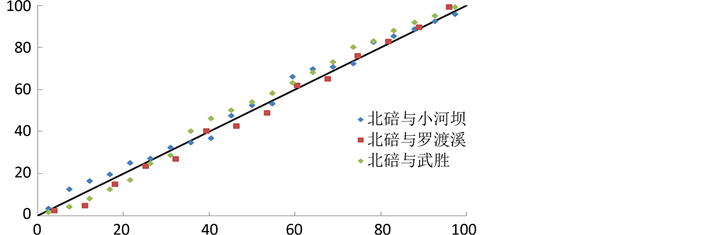
Figure 3. Joint distribution and empirical probabilities of the observed combinations
图3. 北碚与小河坝、罗渡溪、武胜站站联合经验点据及理论分布
量同时都超过特定值时,事件发生的重现期。根据以上得到的小河坝与北碚、武胜与北碚、罗渡溪与北碚的Copula联合分布,计算得到各两站的联合重现期和同现重现期,绘制等值线见图4 (省略了小河坝站与北碚站、武胜站与北碚站的等值线图)。
4.5. 嘉陵江干支流遭遇分析
嘉陵江流域干流与支流小河坝与北碚、武胜与北碚、罗渡溪与北碚的洪水遭遇且发生某一重现期的洪水概率为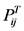 ,
, 公式如下:
公式如下:
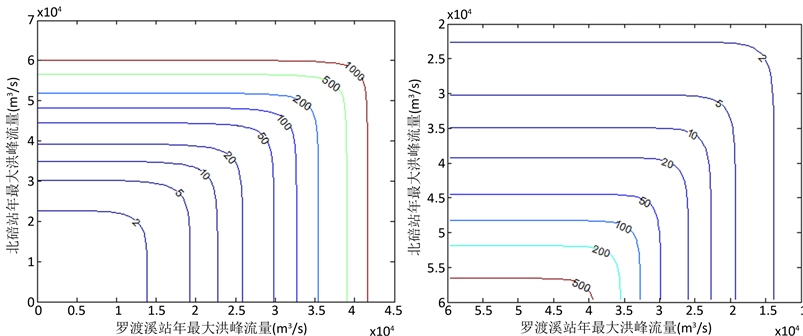
Figure 4. The joint (left) and co-occurrence return periods (right) of Jialing River and its tributaries
图4. 罗渡溪站与北碚站之间的联合重现期(左)和同现重现期(右)等值线图
Table 3. Coincidence risk analysis of flood magnitudes of Jialing River and its tributaries (%)
表3. 嘉陵江流域干流与支流洪水两两遭遇概率(%)
 (9)
(9)
式中: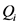 、
、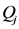 代表
代表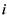 、
、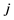 两江的洪水发生的量级,
两江的洪水发生的量级,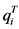 、
、 分别代表
分别代表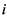 、
、 两江
两江 年一遇的设计洪水。表3列出了嘉陵江流域干流与支流重现期分别为1000年、100年、50年、10年一遇设计洪水值及其遭遇概率。小河坝与北碚、武胜与北碚、罗渡溪与北碚遭遇千年一遇的洪水概率分别为0.000167、0.000581、0.000645,百年一遇的洪水遭遇概率分别为0.001721、0.005849、0.006479。由表可知,同河流,低重现期遭遇洪水概率大于高重现期;同重现期情况下,与嘉陵江干流北碚站的洪水遭遇,罗渡溪遭遇概率大于武胜,小河坝遭遇概率最低,这与计算二维联合分布的Kendall相关系数的大小相对应。说明对于嘉陵江流域,汛期洪水较多是由渠江(罗渡溪)造峰所致,涪江(小河坝)洪水造成北碚站发生同重现期洪水的概率最小。
年一遇的设计洪水。表3列出了嘉陵江流域干流与支流重现期分别为1000年、100年、50年、10年一遇设计洪水值及其遭遇概率。小河坝与北碚、武胜与北碚、罗渡溪与北碚遭遇千年一遇的洪水概率分别为0.000167、0.000581、0.000645,百年一遇的洪水遭遇概率分别为0.001721、0.005849、0.006479。由表可知,同河流,低重现期遭遇洪水概率大于高重现期;同重现期情况下,与嘉陵江干流北碚站的洪水遭遇,罗渡溪遭遇概率大于武胜,小河坝遭遇概率最低,这与计算二维联合分布的Kendall相关系数的大小相对应。说明对于嘉陵江流域,汛期洪水较多是由渠江(罗渡溪)造峰所致,涪江(小河坝)洪水造成北碚站发生同重现期洪水的概率最小。
5. 结论
本文采用二维Gumbel Copula联结函数,构建了嘉陵江干支流洪峰流量的联合分布,边缘分布采用P-III型分布来构建,并分析了嘉陵江干流和支流的洪水遭遇概率。结果表明采用P-III型和Copula函数构建嘉陵江干支流边缘、联合分布拟合情况均较好,相同重现期洪水遭遇组合中,渠江(罗渡溪)与嘉陵江干流下游(北碚)遭遇的概率大于嘉陵江中游(武胜)与嘉陵江干流下游(北碚)遭遇的概率,涪江(小河坝)与嘉陵江干流下游(北碚)遭遇的概率最低。本文采用的计算方法具有理论基础,结果可行,可为嘉陵江流域的洪水规律认识及遭遇分析提供新的理论及研究途径。
文章引用
冉啟香,彭 畅,凌 旋. 基于Copula函数的嘉陵江流域干支流洪水遭遇分析
Flood Coincidence Probability Analysis for Mainstream and Tributaries of the Jialing River Basin Based on Copula Function[J]. 水资源研究, 2017, 06(05): 459-467. http://dx.doi.org/10.12677/JWRR.2017.65054
参考文献 (References)
- 1. 范可旭, 徐长江. 乌江洪水与长江三峡洪水遭遇研究[J]. 水文, 2010, 30(4): 63-65. FAN Kexu, XU Changjiang. Research on meeting of floods from Wujiang River and Three Gorges. Journal of China Hydrology, 2010, 30(4): 63-65. (in Chinese)
- 2. 熊莹. 长江上游干支流洪水组成与遭遇研究[J]. 人民长江, 2012, 43(10): 42-45. XIONG Ying. Research on flood composition and encounter of main streams and tributaries in upper Yangtze River. Yangtze River, 2012, 43(10): 42-45. (in Chinese)
- 3. 张洪刚, 郭海晋, 欧应钧. 长江流域洪水地区组成与遭遇规律研究[J]. 人民长江, 2013, 44(10): 62-65. ZHANG Honggang, GUO Haijin and OU Yingjun. Research on composition and encounter laws of flood in Yangtze River Basin. Yangtze River, 2013, 44(10): 62-65. (in Chinese)
- 4. 郭生练, 闫宝伟, 肖义, 等. Copula函数在多变量水文分析计算中的应用及研究进展[J]. 水文, 2008, 28(3): 1-7. GUO Shenglian, YAN Baowei, XIAO Yi, et al. Application of copula functions in multivariate hydrological analysis and estimation. Journal of China Hydrology, 2008, 28(3): 1-7. (in Chinese)
- 5. 陈璐, 郭生练, 张洪刚, 等. 长江上游干支流洪水遭遇分析[J]. 水科学进展, 2011, 22(3): 323-330. CHEN Lu, GUO Shenglian, ZHANG Honggang, et al. Flood coincidence probability analysis for the upstream Yangtze River and its tributaries. Advances in Water Scinence, 2011, 22(3): 323-330. (in Chinese)
- 6. 闫宝伟, 郭生练, 陈璐, 等. 长江和清江洪水遭遇风险分析[J]. 水利学报, 2010, 41(5): 553-559. YAN Baowei, GUO Shenglian, CHEN Lu, et al. Flood encountering risk analysis for the Yangtze River and Qingjiang River. Shuili Xuebao, 2010, 41(5): 553-559. (in Chinese)
- 7. 关帅, 林颖妍, 查悉妮, 等. 基于Copula函数的韩江流域干支流洪水遭遇分析[J]. 中山大学学报(自然科学报), 2015, 54(5): 130-137. GUAN Shuai, LIN Yingyan, CHA Xini, et al. Copula function-based flood coincidence probability analysis for mainstream and tributary of the Hanjiang River basin. Journal of Sun Yat-sen University (Natural Science News), 2015, 54(5): 130-137. (in Chinese)
- 8. 李天元, 郭生练, 栗飞, 等. 基于copula函数的非连续序列洪水频率分析[J]. 武汉大学学报(工学版), 2011, 44(6): 681-684. LI Tianyuan, GUO Shenglian, LI Fei, et al. Multivariate discontinuous flood frequency analysis using Copulas. Engineering Journal of Wuhan University, 2011, 44(6): 681-684. (in Chinese)
- 9. 苗磊. 西汉水与嘉陵江干流洪水遭遇分析[J]. 地下水, 2011, 33(5): 145-146. MIAO Lei. Flood coincidence probability analysis for mainstream of the Xihanshui River and Jialing River. Ground Water, 2011, 33(5): 145-146. (in Chinese)
- 10. GENEST, C., RIVEST, L.P. Statistical inference procedures for bivariate Archimedean copulas. Journal of the American Statistical Association, 1993, 88(423): 1034-1043.
- 11. 莫淑红, 沈冰, 张晓伟, 等. 基于Copula函数的合川径流丰枯遭遇分析[J]. 西北农林科技大学学报, 2009, 37(6): 131-136. MO Shuhong, SHEN Bing, ZHANG Xiaowei, et al. Synchronous-asynchronous encounter probability of rich-poor runoff based on copula function. Journal of Northwest A&F University, 2009, 37(6): 131-136. (in Chinese)
