Artificial Intelligence and Robotics Research
Vol.07 No.03(2018), Article ID:26621,6
pages
10.12677/AIRR.2018.73015
Building an Intelligent Model Based on Interface
Yebin Lin, Yemin Lin
Found Intelligent Technology Co., Ltd., Hangzhou Zhejiang

Received: Aug. 5th, 2018; accepted: Aug. 20th, 2018; published: Aug. 28th, 2018

ABSTRACT
With the explosive development of AI technology, AI technology has been widely applied in more and more fields. Many algorithms, such as machine learning, deep learning, and so on, show great importance in these fields. Then, there is still an insurmountable gap between the present artificial intelligence technology and the really expected strong artificial intelligence. The aim of this paper is to propose a set of theoretical models based on interface adjustment, which is intended to explore new ways of artificial intelligence implementation, and we hope that in future research, the algorithm model can be a new breakthrough in many directions.
Keywords:Artificial Intelligence, Interface Driver, Algorithm Model
构建以接口作为基础的智能模型
林烨斌,林烨敏
方得智能科技有限公司,浙江 杭州

收稿日期:2018年8月5日;录用日期:2018年8月20日;发布日期:2018年8月28日

摘 要
随着人工智能技术的爆炸式发展,人工智能技术也在越来越多的领域内得到普及应用。机器学习、深度学习等诸多算法在这些领域内大显身手,然后,目前的人工智能技术与真正预期的强人工智能之间仍存在不可逾越的鸿沟。旨在提出一种以接口调节作为基础的一套理论模型,意在探索新的人工智能实现方式,并且希望在今后研究中验证该算法模型在诸多方向上能作为新的突破。
关键词 :人工智能,接口驱动,算法模型

Copyright © 2018 by authors and Hans Publishers Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/


1. 引言
人工智能被定义为研究、开发用于模拟、延伸和扩展人的智能的理论、方法、技术及应用系统的一门新的技术科学 [1] 。目前人工智能应用广泛且普及,追究智能的本质,造成原始智能的基础是通过大自然的筛选和调节,以一种较为优化的方式达到准确的目标 [2] 。我们用数据公式来拟合智能的概念,那么最基本的智能公式可以表达为:智能 = 数据 + 模式(连接方式) + 调节(权值改变) + 目标 [3] 。这里的模式理解为不同数据传导的连接方式,而调节是指在该模式下为达到目标而做的权值优化。目前机器学习等领域最通用的做法都是通过不断的训练学习后,去寻找最优化的权值 [4] ,调节接口的连接是否也能形成一种训练学习,作为获取最优值的一种模式。
2. 模式接口的说明和定义
接口泛指实体把自己提供给外界的一种抽象化物。这里的讨论的接口是指实体与实体之间的连接方式,比如现实生活中,两个个凹凸的物体相互穿插在一起。将这些实体抽象为两个部分,实体本身和实体间的接口。实体通过他们的接口来相互连接。接口连接的方式可以多种多样,比如两个实体通过重力上下叠在一起。那么也可以看成是一种连接,只是连接不太稳定。几乎任何两个相互连接的实体,都可以找到他们之间的接口。
讨论了接口的现实存在方式,那么在数学上又如何去定义这些接口。从最简单数据公式1 + 1 = 2说起。前后两个“1”代表两个实体,而它们中间的“+”号在这里被认为是它们的接口。这样“1 + 1”就看成是两个实体,通过接口连接在一起,形成一个更大的实体。接口普遍存在,它早已渗透在数学里的每个角落。
用“+”和“−”两个符号来定义接口的两种类型,带“+”号的接口把它想象成实体凸出来的那部分,而“−”号接口则表示实体凹进去的那部分。它们两个的相互连接,就符合最简单的加法运算法则,一个“+”接口的权重为4,一个“−”接口的权重也为4,相加为0,结果为0则表示这两个实体进行稳定的连接。从上面分析可以得出,接口包括两个部分,一个正向的接口,一个负向的接口。在接口上引入一个参数(阈值),阈值是判断两个接口是否可以被组合的决定参数。
如果把它们两个相加的值作为接口值的话。那么只要接口的值,小于接口的阈值就可以判断这两个接口是可以连接的。比如设定两个实体的接口阈值是0.2,权重相加的值为0,那么就可以判断为这两个接口是可以连接的。如果是分别为4和−2,相加的绝对值为|4 − 2| > 0.2,那么就判断为不可连接。判断接口连接需要计算接口权值和连接的阈值。
接口组合计算公式:
上面内容完成最简单的两个实体接口组合,基于上述的接口基本单元,来形成一种新的筛选模式和调节方法。接口的阈值和个体接口所带的值是不会改变的,也就是从单个基本实体上来看,是不具备可调节。但是从多个实体的连接的角度上来说,大的正接口既可以通过同样大的负接口进行连接,也可以同时与几个小的负接口来连接。甚至是一个接口,跟附带不同接口的个体连接,也可以形成附带不同接口的整体。因此可以得出的结论是,单个个体接口无法调节,但多个实体接口之间的连接组合方式是可以调节。
3. 接口模式的案例说明
3.1. 接口力传递例子
通过例子来说明他们之间的调节和筛选模式。例子:形成一个类似肌肉的物体,可以支持(X:0, Y:5)起始点的−40N力的输入和(X:10, Y:5)终点40N力的输出。下面列出3个实体的接口情况:
实体1:(F_available:/X_I1,-X_I2,X_I1//threshold_value:/X_I:20,-X_I:40)
实体2:(F_available:/X_I2,-X_I1,-X_I1//threshold_value:/X_I:40,-X_I:20)
实体3:( F_available:/X_I1,-X_I1//threshold_value:/X_I:20,-X_I:20)
首先说明例子阈值的计算。X_I1,X_I2表示两种接口,但都可以跟负的接口连接,只是接口的阈值不相同。比如(X_I1,-X_I1)可以进行连接,然后(X_I2,-X_I2)也可以连接。但他们的差别是,形成接口的阈值不同。(X_I1,-X_I1)的接口连接,两个个接口的阈值都是20,因此取最小值,(X_I1,-X_I1)的C阈值就是20。(X_I2,-X_I2)两个接口的阈值都是40,那么他们形成的接口最小的C阈值也是40。当然也可以(X_I1,-X_I2)进行连接,他们单独接口的阈值分别是20,40,组合成的接口C阈值取最小值的20。
然再说明下例子权值的计算。终点的40N力W正,只要实体跟终点连接W负,那么接口的权值计算为|W正 + W负| = |40 + 0| = 40。根据力传导的关系,终点通过接口把40N的力传导给了这个实体。那么假如这个实体再跟另外两个实体连接的话,两个接口连接的权值分别为:|W正 + W负| = |40/2 + 0| = 20,|W正 + W负| = |40/2 + 0| = 20。
那么上面的例子先来分析下,可以直接跟起始点和终点连接的接口,只有阈值是40的2个接口,但这个接口都包含着另外2个相反的接口。因此只要连接上这种接口一个,都意味着会增加多余的接口了。而不会产生多余接口的,只有2个接口阈值都是20的接口。也就是理论上来说。只要一个阈值为40的接口跟起始点连接,之后都跟两个接口阈值是20的连接,才会保证没有多余的接口。如下图1所示。
通过起始点和终点力的传递关系和接口类型,来进行筛选一个适合起始输入和终点输入的整体。完成这个例子,需要通过筛选3个接口相互叠加的整体,并且通过力的传递和接口类型来判断是否可以连接。理论上,经过筛选就可以形成如上图的整体。当然随着条件的改变,形成的整体也会随着改变。
把实体1(F_available:/X_I,-X_I//threshold_value:/X_I:20,-X_I:20)的阈值变小,变成如下(F_available:/X_I,-X_I//threshold_value:/X_I:10,-X_I:10),那么形成的理论的模型也就会变成中间4条线连接的。改变起始输入和终点输入的力,都会影响和改变着形成的整体。有的需求会出现起始点和终点不在一个水平线上,那么也可以通过添加Y轴类型的接口,这样就会形成一个类似于手臂弯曲的结构。实

Figure 1. Schematic diagram of individual connection
图1. 实体连接示意图
体还包括动态变化的结构,可以形象的理解为弹簧一类,这就可以让形成的整体拥有一定范围内值的变化。
3.2. 接口连接不同结构例子
通过例子简单地说明了下接口模型的运行方式。但对于说明实际的用处来说,还是差了一些的。下面举个偏向实际的例子来进一步分析。假设有这么一个需求,需要拼接一个机器,去采摘随机位置苹果树上的苹果。例子设定:
在这个需求里面,起始点(随机苹果树)的位置参数定为random_X:(0,100),random(0,100),单位为m。然后采摘苹果假设需要−40N的力,终点(苹果的可能位置)为Z轴的随机位置random_Z:(0,10),random_X:(0,100),random(0,100)。设置对应的公式:
起始点:(area:/random_X:(0,100), random(0,100))
终点:(area:/random_Z:(0,10), random_X:(0,100), random(0,100)//value:/40)
拥有的基础的拼接结构包括:
轮子:(F_available:/X_I3//threshold_value:/X_I3:1000//area:/random_XY)
伸缩杆:(F_available:/X_I2//threshold_value:/X_I2:40//area://random_Z:/(0, 1))
抓手:(F_available:/-X_I2//threshold_value:/X_I2:40//value://-40)
实体1:
(F_available:/X_I1,-X_I2,X_I1//threshold_value:/X_I:20,-X_I:40//value:/1)
实体2:
(F_available:/X_I2,-X_I1,-X_I1//threshold_value:/X_I2:40,-X_I:20//value:/1)
实体3:
F_available:/X_I1,-X_I1//threshold_value:/X_I:20,-X_I:20//value:/1)
可结合模型执行过程分析:
1) 根据起始点和终点的属性,分别提取了适合random_X:(0,100),random(0,100),的轮子random_X,random_Y,适合random_Z:(0,10的伸缩杆random_Z,适合−40N力的抓手。
2) 通过实体连接形成适应这些部件的结构
a) 抓手:
抓手输出−40N的力,那么就需要实体形成适应抓手的接口-X_I2和40N力的形状。可以通过实体2的X_I2接口来连接
b) 伸缩杆:
因为苹果的位置是random_Z(0,10),伸缩杆的长度变化是random_Z:/(0,1),那么需要10个伸缩杆相互连接了。而实体块则需要形成伸缩杆之间连接的桥梁,可以通过实体3的X_I1,-X_I1接口前后相连。
c) 轮子:
轮子的接口X_I3可以跟任何实体接口相连接,但要形成一个整体接口阈值比较大的结构来承受压力。
3)形成的构件之间的相互连接
a) 抓手-伸缩杆:
抓手构件要−40N的力,伸缩杆构件的阈值是20,那么就需要2个伸缩杆的构件来支撑。也就是20根伸缩杆和它们连接的组成。这样形成之后,一个可以上下移动和抓取的手臂构件就形成了。
b) 手臂构件-轮子构件:
手臂构件的接口包括伸缩杆和壳的接口,同时手臂构件的力也会传递下来。那么就需要形成一个适应手臂构件的接口和力的结构,同时跟轮子构件连接。形成车身的实体的总的重量value,也要大于手臂结构传递下来的力。然后通过接口暴露最少性,结构最少的需求筛选构架,形成了车子的身体。
那么通过以上步骤,就可以把需求通过接口模型实现出来了。当然上面只是形成一个车子的模型,至于行驶和驱动也还需要发动机啊,人的驾驶啊等,但这些就不属于可结合模型的形成内容了。然后上面提供的初始部件,伸缩杆,抓手,轮子也是可以通过更小的基础部件形成的,只是那样太过于繁琐,就不继续讨论下去了。也就是通过例子,可以看出接口模型,可以形成适应需求的整体。
上面的例子看起来有点不可思议,一个单一的需求,却可以形成不同构件的整体。但假如理解了接口模型,传递的不仅仅是力,也可以传递前后部件的接口,那么就可以理解把不同部件组合在一起形成整体的过程。接口模型跟人类基因组结合类似。基因是由碱基对经过自然筛选,并且让整体形成适应这些接口的整体。基因平时也是相反的基因来闭合的,只有打开的时候,它的筛选才是激活的,这也跟接口模式的筛选相近。接口模型可以类似基因一样,通过接口形成复杂的个体。
4. 接口模式与传统算法的比较
相对于传统算法来说,接口算法是一种筛选调整的算法。它只需要知道前后的筛选条件,接口和它们的计算关系,就可以得到结果。
相对于神经网络算法来说。它们两个都是通过学习来调整参数的算法。神经网络算法是针对权值的调整,也就是初始值通过调整可以变成目标值。如图2。神经网络算法的使用场景是起始输入通过调整可以到达目标输出。
接口模型是针对于接口的调整,也就是形成一个整体把初始值和目标值连接在一起。如图3。从使用层面来看,接口模型是接口调整形成整体的过程。接口模型的使用场景是起始输入通过调节接口可以跟目标输出相连接。
5. 接口模式的应用场景
接口模型适用范围极广,因为它是形成一个可以执行结果的个体,神经网络是形成可以执行结果的操作 [5] 。它们也是不冲突的,相当于给予一个目标,那么可以通过接口模型,连接基本的物质构成一个可以执行的个体,然后通过神经网络模型,训练这个个体怎么执行的更加准确。举一些例子,比如建造

Figure 2. MP neuron model
图2. M-P神经元模型
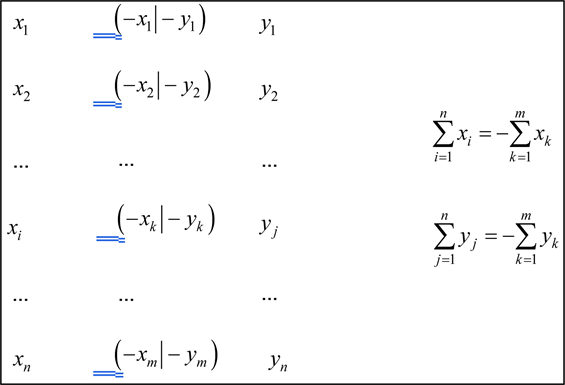
Figure 3. Interface algorithm model
图3. 接口模型
房子,通过整体的稳定性,内部空间的大小,整体的美观来筛选形成的整体。那么就可以形成生活中常见的房子。当然也可能是更多样的形式,可以参考生物形成的蜂巢,蚂蚁的洞穴等。
比较具体的类似于树叶的形成,通过获取阳光的量来调节细胞的连接形成。那么在下面的细胞,接收阳光少,所以就不会往厚度方面连接,而是往水平方向连接,因此可以形成叶子的扁平个体。然后根据其它的筛选因素也可以形成各式各样的叶子,比如北方的雪大,那么要求叶子承受面积小会成为筛选的因素,从而形成松树的针叶。热带雨林的降雨比较大,也可以形成类似于香蕉树叶的方便水流。添加不同的因素,可以形成适应这些因素的个体。并且形成的个体因为是接口相互连接的,因此也可以拥有修复的功能。例如在叶子旁边,撕破一个小口,整体的接口也会被激活,然后继续修复这个缺口。
文章引用
林烨斌,林烨敏. 构建以接口作为基础的智能模型
Building an Intelligent Model Based on Interface[J]. 人工智能与机器人研究, 2018, 07(03): 129-134. https://doi.org/10.12677/AIRR.2018.73015
参考文献
- 1. 张博宇. 网络背景下人工智能技术的应用[J]. 科技资讯, 2016(36): 18-20.
- 2. 张储祺. 计算机人工智能技术的应用与发展[J]. 电子世界, 2017(2): 41-43.
- 3. [德]海德格尔. 存在与时间[M]. 陈嘉映, 王庆节, 译. 北京: 三联书店, 1999.
- 4. 刘挺, 车万翔. 自然语言处理中的知识获取问题[J]. 中国计算机学会通讯, 2017(5).
- 5. Anderson, M. (2003) Embodied Cognition: A Field Guide. Artificial Intelligence, No. 149.