Advances in Applied Mathematics
Vol.3 No.04(2014), Article
ID:14350,8
pages
DOI:10.12677/AAM.2014.34028
The Optimal K-Duals for 1-Erasure for Parseval K-Frames
Department of Mathematics, Nanjing University of Aeronautics and Astronautics, Nanjing
Email: liliang1100@126.com, pengtongli@nuaa.edu.cn
Copyright © 2014 by authors and Hans Publishers Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/



Received: Aug. 20th, 2014; revised: Sep. 22nd, 2014; accepted: Oct. 2nd, 2014
ABSTRACT
In this paper, we introduce the concept of K-dual. We investigate the K-duals that are optimal for erasures for Parseval K-frames in finite Hilbert spaces. We will give the necessary and sufficient conditions under which the canonical K-dual is the unique optimal K-duals for erasures. We also discuss some special conditions under which the canonical K-dual is not the optimal K-dual or optimal K-dual but not the unique one.
Keywords:K-frame, Optimal K-dual, Erasure

Parseval K-框架的1-丢失最佳K-对偶
李 亮,李鹏同
南京航空航天大学,数学系,南京
Email: liliang1100@126.com, pengtongli@nuaa.edu.cn
收稿日期:2014年8月20日;修回日期:2014年9月22日;录用日期:2014年10月2日

摘 要
本文引入K-对偶的概念,对有限维Hilbert空间的Parseval K-框架,利用K-对偶来研究在丢失意义下的最佳 K-对偶。本文讨论了Parseval K-框架的典则K-对偶是唯一最佳K-对偶的充分必要条件。并讨论了在某些特殊条件下典则K-对偶不是最佳K-对偶或者不是唯一的最佳K-对偶。
关键词
K-框架,最佳K-对偶,丢失

1. 引言
近些年来研究者从编码学的角度对框架进行研究[1] -[3] ,试图找到最好的紧框架。从而引发了寻求在丢失意义下最佳框架的研究。通常要在编码之前选择最佳框架,使得在发生信号(系数坐标)丢失后,用最佳框架重构的信号(向量)与原始信号(向量)之间的误差达到最小。然后用这些最佳框架进行编码和解码。众所周知,一致紧框架对1-丢失而言是最佳紧框架,而等角框架是2-丢失最佳框架[3] 。由于这种重构思想带有一定的局限性,只能选择有自对偶性质的Parseval框架进行重构。而实际应用中,可能要求编码框架和解码框架不同。在[4] [5] 中,对已选择地编码框架(不一定是紧的),如果在传输过程中一些系数坐标发生丢失,则选择其对偶框架进行重构,使得重构信号与原始信号误差最小。这类框架称为对丢失而言的最佳对偶框架。
2012年,Gǎvruta在研究关于有界线性算子的原子分解时引入并研究了一种比经典框架[6] [7] 更一般的概念,即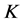 -框架[8] 。之后,文献[9] [10] 对这一类新的框架也进行了研究,讨论了紧
-框架[8] 。之后,文献[9] [10] 对这一类新的框架也进行了研究,讨论了紧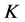 -框架以及
-框架以及 -框架的扰动等问题。把框架研究的范围限制在了子空间
-框架的扰动等问题。把框架研究的范围限制在了子空间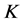 的值域
的值域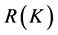 上。本文将介绍
上。本文将介绍 -对偶的概念,在有限维Hilbert空间上,把用对偶框架重构信号的思想用在
-对偶的概念,在有限维Hilbert空间上,把用对偶框架重构信号的思想用在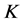 -框架上,利用
-框架上,利用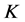 -对偶来重构
-对偶来重构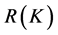 上的信号“
上的信号“ ”而不是整个空间上的的信号“
”而不是整个空间上的的信号“ ”。通过Parseval
”。通过Parseval -框架的典则对偶研究使得Parseval
-框架的典则对偶研究使得Parseval 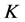 -框架存在丢失意义下唯一最佳
-框架存在丢失意义下唯一最佳 -对偶的条件。
-对偶的条件。
本文采用如下记号: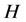 表示可分Hilbert空间,
表示可分Hilbert空间, 表示
表示 上的恒等算子。
上的恒等算子。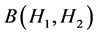 表示
表示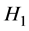 到
到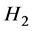 的有界线性算子的集合。特别地,
的有界线性算子的集合。特别地,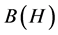 表示从
表示从 到
到 的有界线性算子的集合。对任意的
的有界线性算子的集合。对任意的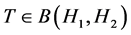 ,
,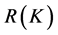 或
或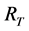 表示算子
表示算子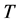 的值域,
的值域,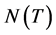 或
或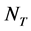 表示
表示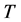 的核,
的核, 表示
表示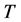 的共轭算子。
的共轭算子。
2. 预备知识
本节将介绍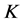 -框架,
-框架,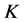 -对偶的基本概念和最佳
-对偶的基本概念和最佳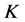 -对偶的研究方案。
-对偶的研究方案。
定义2.1 [8] -[10] 设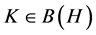 ,序列
,序列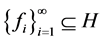 称为
称为 的
的 -框架,如果存在常数
-框架,如果存在常数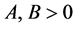 使得
使得
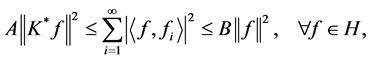 (2.1)
(2.1)
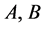 分别称为框架
分别称为框架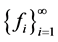 的下界,上界。特别地,如果
的下界,上界。特别地,如果
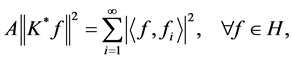
则称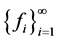 为
为 的紧
的紧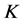 -框架。如果在上式中
-框架。如果在上式中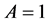 ,则称相应的紧
,则称相应的紧 -框架
-框架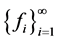 为
为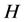 的Parseval
的Parseval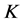 -框架。
-框架。
下面是 -框架的几个等价条件。
-框架的几个等价条件。
引理2.1 [8] 设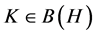 ,序列
,序列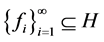 ,则下列叙述是等价的:
,则下列叙述是等价的:
1) 是
是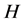 的一个
的一个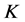 -框架;
-框架;
2) 是Bessel序列,且存在Bessel序列
是Bessel序列,且存在Bessel序列 ,使得
,使得
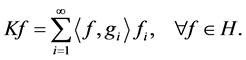 (2.2)
(2.2)
设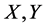 是Banach空间,
是Banach空间,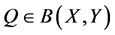 是闭值域的。若
是闭值域的。若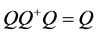 ,则称
,则称 为
为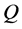 的伪逆。特别地,
的伪逆。特别地, 。一般来说
。一般来说 的伪逆是不唯一的,下面是
的伪逆是不唯一的,下面是 的伪逆唯一的充要条件。
的伪逆唯一的充要条件。
引理2.2 [11] 设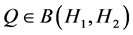 ,且
,且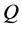 是闭值域的,则
是闭值域的,则 的伪逆
的伪逆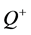 唯一存在的充分必要条件是:
唯一存在的充分必要条件是:
1)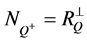 ;
;
2)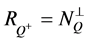 ;
;
3) .
.
定义2.2 满足引理2.1(2.2)式的Bessel序列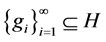 称为
称为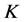 -框架
-框架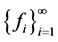 的
的 -对偶。
-对偶。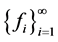 是
是 的
的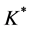 对偶。
对偶。
称(2.2)式为 -框架的重构公式。特别地,若
-框架的重构公式。特别地,若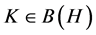 是闭值域的,并且
是闭值域的,并且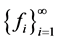 是Parseval
是Parseval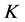 -框架,
-框架, 满足(2.2)式,称
满足(2.2)式,称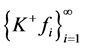 为Parseval
为Parseval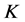 -框架
-框架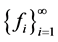 的典则
的典则 -对偶。
-对偶。
在编码理论中,可以用框架 通过其分析算子
通过其分析算子 将
将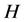 上的向量(信号)
上的向量(信号) 编码为
编码为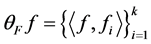 ,然后传送给接收者,再由接收者来解码而后重构信号
,然后传送给接收者,再由接收者来解码而后重构信号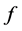 。在最后的解码过程中需要用到其对偶框架。但是在传输过程中,可能会丢失编码信息
。在最后的解码过程中需要用到其对偶框架。但是在传输过程中,可能会丢失编码信息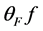 中的系数。由于框架有冗余的性质,可以用剩余的系数来重构原始信号
中的系数。由于框架有冗余的性质,可以用剩余的系数来重构原始信号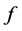 。但是由于丢失系数的位置不确定,重构工作可能有些复杂,这时可用最佳逼近的思想用典则对偶框架去重构原始信号。
。但是由于丢失系数的位置不确定,重构工作可能有些复杂,这时可用最佳逼近的思想用典则对偶框架去重构原始信号。
一般的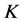 -框架
-框架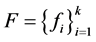 ,由引理2.1(2.2)式得
,由引理2.1(2.2)式得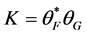 ,其中
,其中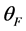 ,
, 分别为
分别为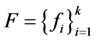 ,
,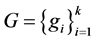 的分析算子。从而可以利用
的分析算子。从而可以利用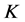 -对偶去重构原始信号“
-对偶去重构原始信号“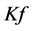 ”。在丢失一部分系数后用接收到的系数去重构原始信号。假设接收到的系数是
”。在丢失一部分系数后用接收到的系数去重构原始信号。假设接收到的系数是 ,其中
,其中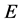 是对角线为
是对角线为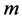 个0和
个0和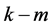 个1的
个1的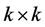 矩阵,
矩阵, 个0的位置与丢失系数的位置相应.这样重构后的信号
个0的位置与丢失系数的位置相应.这样重构后的信号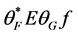 与原始信号
与原始信号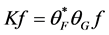 的误差为
的误差为
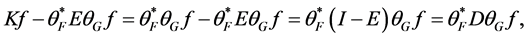
其中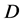 是对角线为
是对角线为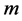 个1和
个1和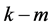 个0的
个0的 矩阵,
矩阵,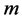 个1的位置与丢失系数的位置相应。用
个1的位置与丢失系数的位置相应。用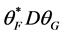 表示丢失
表示丢失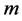 个系数的误差算子。这样只要使得某种意义下的误差最小,就使得重构后的信号与原始信号最接近。
个系数的误差算子。这样只要使得某种意义下的误差最小,就使得重构后的信号与原始信号最接近。
设 是
是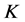 -框架,定义
-框架,定义
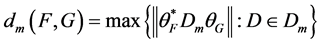 ,
,
其中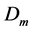 是所有对角线为
是所有对角线为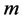 个1和
个1和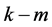 个0的
个0的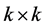 矩阵的集合。
矩阵的集合。
若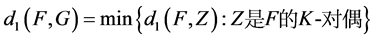 ,则称
,则称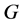 是
是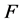 的1-丢失最佳
的1-丢失最佳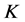 -对偶。
-对偶。
若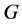 是
是 的
的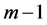 -丢失最佳
-丢失最佳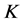 -对偶,且
-对偶,且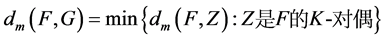 ,则称
,则称 是
是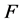 的
的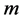 -丢失最佳
-丢失最佳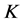 -对偶。
-对偶。
由于Parseval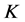 -框架存在特殊的
-框架存在特殊的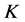 -对偶(典则
-对偶(典则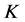 -对偶),即
-对偶),即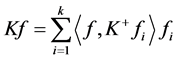 ,可以用典则
,可以用典则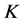 -对偶来重构原始信号。本文主要讨论Parseval
-对偶来重构原始信号。本文主要讨论Parseval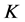 -框架的最佳
-框架的最佳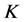 -对偶。
-对偶。
Parseval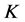 -框架的所有
-框架的所有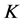 -对偶可用典则
-对偶可用典则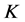 -对偶来构造,即
-对偶来构造,即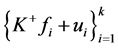 ,其中
,其中 是与
是与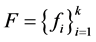 正交的Bessel序列。用
正交的Bessel序列。用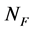 表示所有与
表示所有与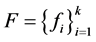 正交的Bessel序列
正交的Bessel序列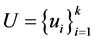 的集合,即
的集合,即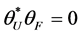 。则
。则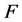 的
的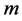 -丢失最佳
-丢失最佳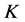 -对偶的形式为:
-对偶的形式为:

下面先说明这样定义的最佳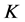 -对偶的存在性。
-对偶的存在性。
任意 ,用
,用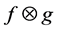 表示秩-1算子,即
表示秩-1算子,即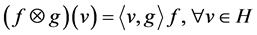 。从而有
。从而有
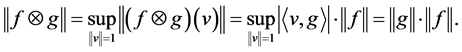
令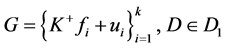 ,则
,则
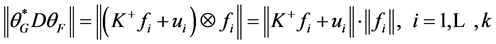 .
.
再定义 。显然
。显然 连续,其中
连续,其中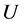 可以看成
可以看成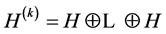 上的向量,从而限制在
上的向量,从而限制在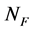 有界子集上最小值存在。
有界子集上最小值存在。
从而将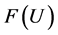 最小化是可以做到的,即1-丢失最佳
最小化是可以做到的,即1-丢失最佳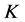 -对偶是存在的。进而
-对偶是存在的。进而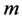 -丢失最佳
-丢失最佳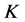 -对偶也存在.而且所有
-对偶也存在.而且所有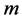 -丢失最佳
-丢失最佳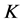 -对偶组成
-对偶组成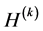 的一个凸,闭,有界子集。
的一个凸,闭,有界子集。
3. 主要结论
本节主要介绍Parseval -框架的典则
-框架的典则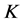 -对偶是唯一最佳
-对偶是唯一最佳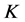 -对偶的充分必要条件。并讨论了典则
-对偶的充分必要条件。并讨论了典则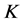 -对偶不是最佳
-对偶不是最佳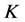 -对偶或者不是唯一的最佳
-对偶或者不是唯一的最佳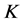 -对偶的充分条件。
-对偶的充分条件。
下面将说明在一定条件下,Parseval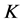 -框架的典则
-框架的典则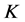 -对偶是唯一的1-丢失最佳
-对偶是唯一的1-丢失最佳 -对偶,进而是
-对偶,进而是 -丢失最佳
-丢失最佳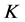 -对偶。
-对偶。
定理3.1 设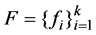 是Parseval
是Parseval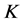 -框架,若满足条件
-框架,若满足条件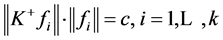 ,其中
,其中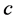 为常数,则
为常数,则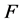 的典则
的典则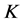 -对偶是唯一的1-丢失最佳
-对偶是唯一的1-丢失最佳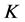 -对偶。
-对偶。
证明 设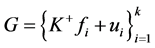 是
是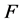 的1-丢失最佳
的1-丢失最佳 -对偶,其中
-对偶,其中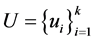 是与
是与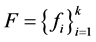 正交的Bessel序列,则
正交的Bessel序列,则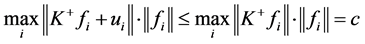 ,从而
,从而
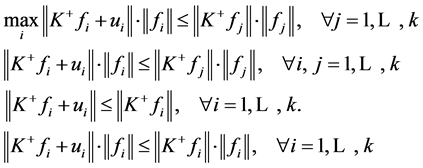
又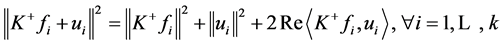 ,进而
,进而
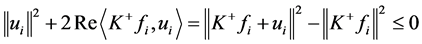 。
。
故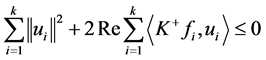 。即
。即
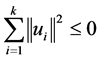 ,
,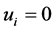 . □
. □
推论3.1 设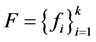 是等范数Parseval
是等范数Parseval -框架,若满足条件
-框架,若满足条件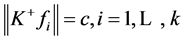 ,其中
,其中
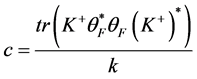 ,
,
 是
是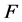 的分析算子。则
的分析算子。则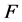 的典则
的典则 -对偶
-对偶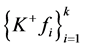 是唯一的1-丢失最佳
是唯一的1-丢失最佳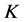 -对偶。
-对偶。
设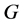 是一个群,
是一个群, 是一个同构映射,其中
是一个同构映射,其中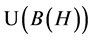 表示
表示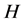 上酉算子构成的群。若
上酉算子构成的群。若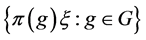 是
是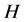 上的
上的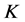 -框架,则称为群表示
-框架,则称为群表示 -框架,其中
-框架,其中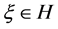 。用
。用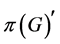 表示与
表示与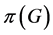 可交换的有界线性算子的集合。
可交换的有界线性算子的集合。
推论3.2 设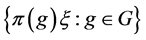 是Parseval
是Parseval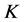 -框架,若满足条件
-框架,若满足条件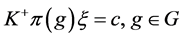 ,其中
,其中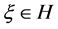 。则
。则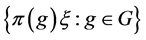 的典则
的典则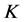 -对偶
-对偶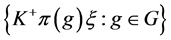 是唯一的1-丢失最佳
是唯一的1-丢失最佳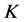 -对偶。
-对偶。
引理3.1 设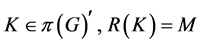 是
是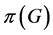 的不变子空间,
的不变子空间,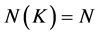 也是
也是 的不变子空间,则
的不变子空间,则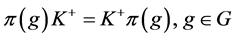 。
。
证明 设任意的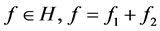 ,其中
,其中 。由
。由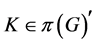 得
得
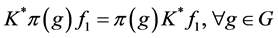 ,
,
则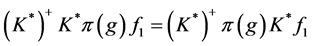 。由
。由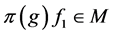 得
得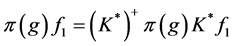 。令
。令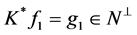 ,则
,则
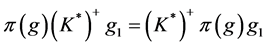 .
.
又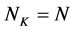 也是
也是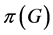 的不变子空间,则
的不变子空间,则
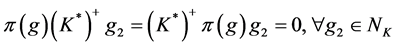 .
.
从而 ,即
,即
 ,
,
进而
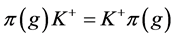 .□
.□
推论3.3 设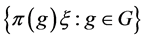 是Parseval
是Parseval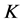 -框架,若满足条件
-框架,若满足条件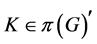 ,
, 是
是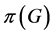 的不变子空间,
的不变子空间,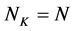 也是
也是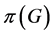 的不变子空间,则
的不变子空间,则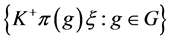 是唯一的1-丢失最佳
是唯一的1-丢失最佳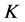 -对偶。
-对偶。
设序列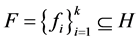 ,若
,若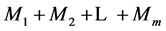 是直和,即
是直和,即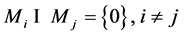 ,其中
,其中
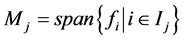 ,则称
,则称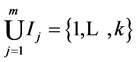 是
是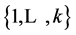 的
的 -线性无关分解。
-线性无关分解。
下面是比定理3.1更一般的情况。
定理3.2 设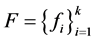 是Parseval
是Parseval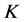 -框架,
-框架,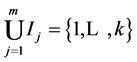 是
是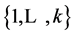 的
的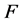 -线性无关分解,
-线性无关分解,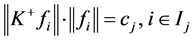 ,则
,则
1)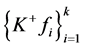 是1-丢失最佳
是1-丢失最佳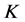 -对偶;
-对偶;
2) 设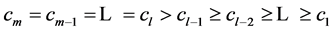 ,则
,则 存在唯一的1-丢失最佳
存在唯一的1-丢失最佳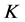 -对偶的充分必要是
-对偶的充分必要是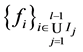 是线性无关的。
是线性无关的。
证明 1) 设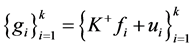 是
是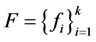 的1-丢失最佳
的1-丢失最佳 -对偶,其中
-对偶,其中 ,即
,即
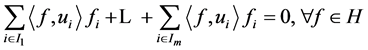 .
.
由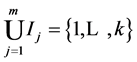 是
是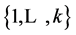 的
的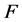 -线性无关分解得,
-线性无关分解得,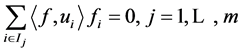 。令
。令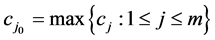 ,则由
,则由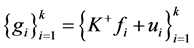 是
是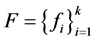 的1-丢失最佳
的1-丢失最佳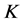 -对偶得对任意
-对偶得对任意 ,
,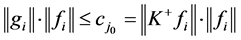 ,即
,即 。从而由定理3.1证明过程得
。从而由定理3.1证明过程得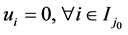 ,则
,则

得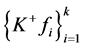 是1-丢失最佳
是1-丢失最佳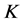 -对偶,但不是唯一的最佳
-对偶,但不是唯一的最佳 -对偶。
-对偶。
2) 设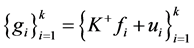 是
是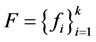 的1-丢失最佳
的1-丢失最佳 -对偶,由(1)可知,
-对偶,由(1)可知,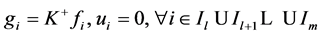 。则
。则
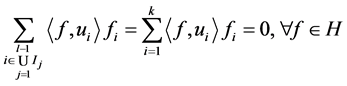 .
.
充分性。由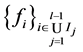 是线性无关的得
是线性无关的得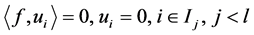 。从而
。从而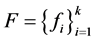 存在唯一的1-丢失最佳
存在唯一的1-丢失最佳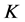 -对偶。
-对偶。
必要性。假设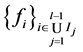 是线性相关的,则由
是线性相关的,则由 得,
得,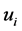 不全为
不全为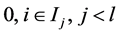 。则
。则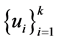 为非零序列,且
为非零序列,且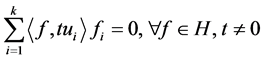 。
。
从而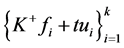 是
是 的
的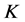 -对偶。又
-对偶。又 ,则存在
,则存在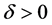 ,使得
,使得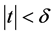 时,
时,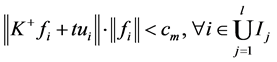 ,从而
,从而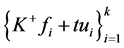 是
是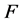 的1-丢失最佳
的1-丢失最佳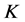 -对偶,与
-对偶,与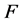 的1-丢失最佳
的1-丢失最佳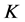 -对偶是唯一的相矛盾。□
-对偶是唯一的相矛盾。□
设
 ,
,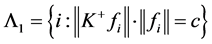 ,
,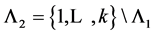 。
。
 .
.
下面再给出典则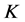 -对偶是唯一的1-丢失最佳
-对偶是唯一的1-丢失最佳 -对偶的一个充要条件。
-对偶的一个充要条件。
定理3.3 设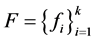 是Parseval
是Parseval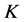 -框架,则下列是等价的:
-框架,则下列是等价的:
1) 是唯一的1-丢失最佳
是唯一的1-丢失最佳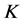 -对偶;
-对偶;
2)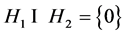 且
且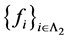 是线性无关的。
是线性无关的。
证明 (1)Þ(2)。假设 是线性相关的,则任意
是线性相关的,则任意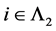 ,存在不全为零的
,存在不全为零的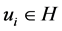 使得
使得
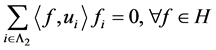 .
.
令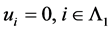 。则
。则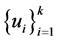 是非零序列,
是非零序列,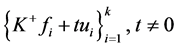 是
是 的
的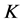 -对偶,且
-对偶,且
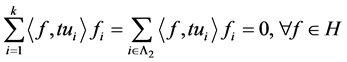 .
.
又
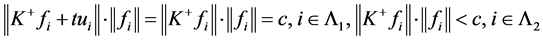 ,
,
则存在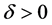 使得
使得 时,
时, 。从而
。从而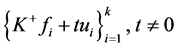 ,是
,是 的1-丢失最佳
的1-丢失最佳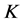 -对偶,与
-对偶,与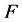 的1-丢失最佳
的1-丢失最佳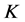 -对偶是唯一的相矛盾。
-对偶是唯一的相矛盾。
下证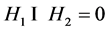 。
。
假设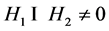 ,则存在线性无关的集合
,则存在线性无关的集合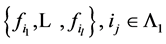 和不全为零的数
和不全为零的数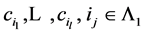 ,使得
,使得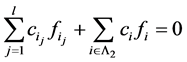 。
。
由 是线性无关的,则存在
是线性无关的,则存在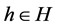 使得
使得
 .
.
事实上,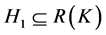 (否则,
(否则,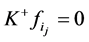 ,
, 显然)。由
显然)。由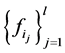 是线性无关的,从而
是线性无关的,从而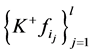 是线性无关的,则是
是线性无关的,则是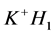 的一组基,从而存在对偶基
的一组基,从而存在对偶基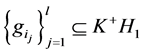 使得
使得
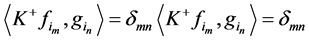 ,
,
其中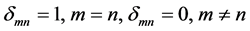 。只需令
。只需令 即可。
即可。
令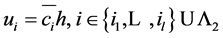 ,且
,且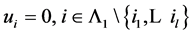 。则任意
。则任意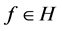 ,
,
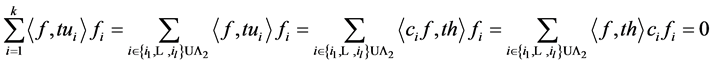
从而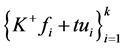 是
是 的
的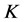 -对偶,其中
-对偶,其中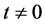 。又
。又 。存在
。存在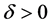 使得
使得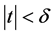 时,
时,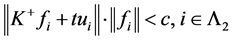 ,且
,且
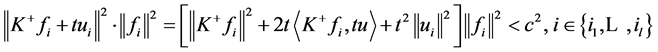 .
.
则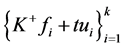 是
是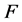 的最佳1-丢失最佳
的最佳1-丢失最佳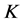 -对偶.与
-对偶.与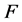 的1-丢失最佳
的1-丢失最佳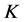 -对偶是唯一的相矛盾。
-对偶是唯一的相矛盾。
(2)Þ(1)。设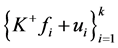 是
是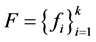 的1-丢失最佳
的1-丢失最佳 -对偶,其中
-对偶,其中 ,即
,即
 .
.
由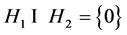 知,
知,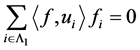 ,
,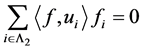 。再由
。再由 是线性无关的得
是线性无关的得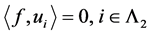 ,即
,即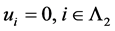 。设
。设 分别为
分别为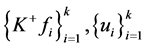 的分析算子。由
的分析算子。由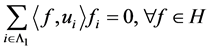 ,可知
,可知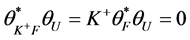 。从而
。从而
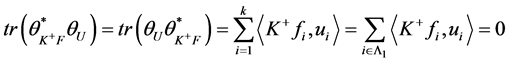 .
.
因 是
是 的1-丢失最佳
的1-丢失最佳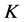 -对偶,则
-对偶,则 ,即
,即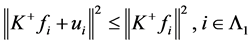 。从而
。从而
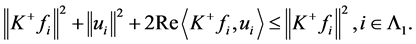
进而,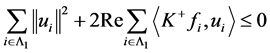 。即
。即
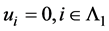 . □
. □
下面给出一个典则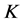 -对偶不是唯一的1-丢失最佳
-对偶不是唯一的1-丢失最佳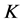 -对偶的充分条件。
-对偶的充分条件。
定理3.4 设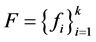 是Parseval
是Parseval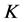 -框架,
-框架,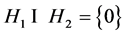 且
且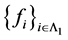 是线性无关的。则
是线性无关的。则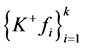 是1-丢失最佳
是1-丢失最佳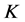 -对偶。特别地,
-对偶。特别地,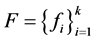 是线性相关的Parseval
是线性相关的Parseval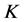 -框架时,
-框架时, 不是唯一的1-丢失最佳
不是唯一的1-丢失最佳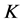 -对偶。
-对偶。
证明 设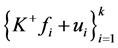 是
是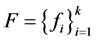 的
的 -对偶,其中
-对偶,其中 ,即
,即
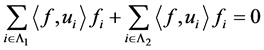 .
.
由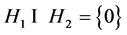 得
得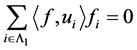 ,且
,且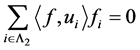 。
。
又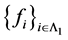 是线性无关的,有
是线性无关的,有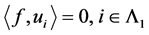 ,即
,即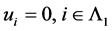 。则
。则
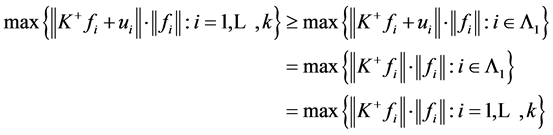
从而 是1-丢失最佳
是1-丢失最佳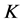 -对偶。
-对偶。
由于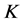 -框架的
-框架的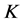 -对偶唯一的充要条件是
-对偶唯一的充要条件是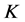 -框架是线性无关的。从而当
-框架是线性无关的。从而当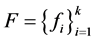 是线性相关的Parseval
是线性相关的Parseval -框架时,
-框架时,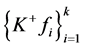 不是唯一的
不是唯一的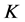 -对偶,则存在
-对偶,则存在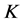 -对偶
-对偶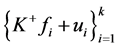 ,当
,当 时,
时,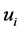 不全为零.由
不全为零.由 知,存在
知,存在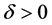 使得
使得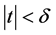 时,
时,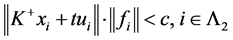 。从而
。从而 是
是 的1-丢失最佳
的1-丢失最佳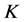 -对偶。□
-对偶。□
下面将说明在一定条件下,典则 -对偶不是1-丢失最佳
-对偶不是1-丢失最佳 -对偶。
-对偶。
定理3.5 设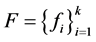 是Parseval
是Parseval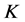 -框架,
-框架, 是线性无关的,存在
是线性无关的,存在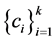 使得
使得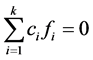 ,且
,且 ,
,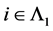 。则
。则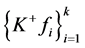 不是
不是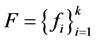 的1-丢失最佳
的1-丢失最佳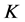 -对偶。
-对偶。
证明 因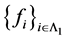 是线性无关的,则由定理3.3证明过程可得,存在
是线性无关的,则由定理3.3证明过程可得,存在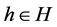 使得
使得
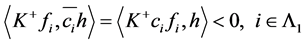 。
。
令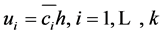 ,则任意
,则任意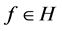 有
有
 ,
,
其中 。从而
。从而 是
是 的
的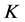 -对偶。从而存在
-对偶。从而存在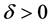 使得
使得 时,
时,
 。
。
且
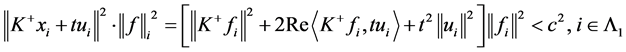 。
。
即 。
。
故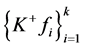 不是
不是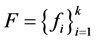 的1-丢失最佳
的1-丢失最佳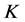 -对偶。□
-对偶。□
推论3.4 设 是Parseval
是Parseval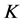 -框架,
-框架,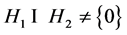 且
且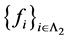 是线性无关的,
是线性无关的,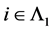 只有一个元素。则
只有一个元素。则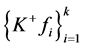 不是
不是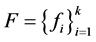 的1-丢失最佳
的1-丢失最佳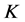 -对偶。
-对偶。
证明 设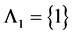 。由
。由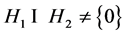 得
得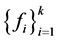 是线性相关的,即存在非零序列
是线性相关的,即存在非零序列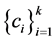 使得
使得
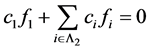 。
。
又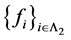 是线性无关的,则
是线性无关的,则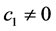 。由定理3.5得
。由定理3.5得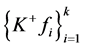 不是
不是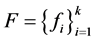 的1-丢失最佳
的1-丢失最佳 -对偶。□
-对偶。□
基金项目
江苏省自然科学基金(No. BK2011720)资助课题。
参考文献 (References)
- [1] Casazza, P.G. and Kovačević, J. (2003) Equal-Norm tight frames with erasures. Advances in Computational Mathematics, 18, 387-430.
- [2] Goyal, V.K., Kovačević J. and Kelner, J.A. (2001) Quantized frame expansions with erasures. Applied and Computational Harmonic Analysis, 10, 203-233.
- [3] Holmes R.B. and Paulsen V.I. (2004) Optimal frames for erasures. Linear Algebra and Its Applications, 377, 31-51.
- [4] Lopez, J.S. and Han, D.G. (2010) Optimal dual frames for erasures. Linear Algebra and Its Applications, 432, 471-482.
- [5] Leng, J.S. and Han D.G. (2011) Optimal dual frames for erasures II. Linear Algebra and Its Applications, 435, 1464- 1472.
- [6] Christensen, O. (2003) An introduction to frames and riesz bases. Birkhauser, Boston.
- [7] Han, D.G. and Larson D.R. (2000) Frames, bases and group representations. Memoirs of the American Mathematical Society, 697, 1-94.
- [8] Gǎvruta, L. (2012) Frames for operators. Applied and Computational Harmonic Analysis, 32, 139-144.
- [9] Xiao, X.C., Zhu, Y.C. and Gavruta, L. (2013) Some properties of K-frames in Hilbert spaces. Results in Mathematics, 63, 1243-1255.
- [10] 丁明玲, 肖祥春, 曾晓明 (2013) Hilbert空间中的紧K-框架. 数学学报, 56, 105-112.
- [11] Christensen, O. (1995) Frames and pseudo-inverse. The Journal of Mathematical Analysis and Applications, 195, 401- 414.