ABSTRACT

In this work, we propose a compact finite volume method for solving the one-dimensional nonlinear sine-Gordon equation. The third-order SSP Runge-Kutta (RK) scheme is used for temporal disretization. Numerical experiments show that the present scheme is an efficient algorithm for solving the one-dimensional Sine-Gordon equation.

Keywords:Sine-Gordon, Compact Method, Finite Volume Method, Runge-Kutta Method

一维Sine-Gordon方程四阶紧致有限体积方法

刘盎然，高巍，李宏

内蒙古大学数学科学学院，内蒙古 呼和浩特

Email: liuang_ran@163.com, gaow@imu.edu.cn, smslh@imu.edu.cn

收稿日期：2015年7月29日；录用日期：2015年8月11日；发布日期：2015年8月18日

摘 要

本文提出一个高阶方法来数值求解非线性Sine-Gordon方程。空间离散上应用四阶的紧致有限体积格式，时间离散应用三阶SSP Runge-Kutta (RK)方法。数值实验表明该算法是求解一维Sine-Gordon方程的较为高效的方法。

关键词 :Sine-Gordon，有限体积紧格式，Runge-Kutta方法

1. 引言

一维Sine-Gordon方程是重要的非线性数学物理方程，可以用来描述流体力学、气象学、场论等领域很多物理现象。例如，传播中的磁通量子两个超导体之间的约瑟夫逊结[1] ，严格的钟摆的运动在拉伸线[2] 、固体物理、非线性光学、流体运动的稳定性。人们对此已经用一些方法作了研究。例如，显式有限差分格式和隐格式离散能量守恒方法[3] 。Strauss and Vázquez [4] ，使用经典的有限差分格式[5] [6] ，计算了Klein-Gordon方程。而[7] 的作者提出了一个使用基函数的方法。Ramos [8] 使用五点隐式有限差分方法。[9] 提出了一种通用的解决Sine-Gordon方程的辛方法。Batiha et al. [10] 给出了一个变分迭代法来获得Sine-Gordon方程的近似解。[11] 是将Sine-Gordon方程转化为一阶非线性初值问题，然后利用递归矩阵在时间和空间近似的二阶方法。Bratsos [12] 提出了一种二阶的空间精度和四阶的时间精度的方法。

在本文中，我们利用紧致四阶有限体积方法离散空间导数，用稳定的三阶Runge-Kutta方法求解一阶常微分方程组。文章框架如下，第一节为引言。第二节构造求解Sine-Gordon方程所使用的4阶紧致有限体积方法。第三节给出时间离散方法，即Runge-Kutta方法；第四节两个典型算例及计算结果讨论。

一维Sine-Gordon方程如下：

(1)

初始条件为

(2)

边界条件为

(3)

为了方便研究能量守恒关系，代入

(4)

其中是一个常数，那么方程(1)可以变化为非线性常微分方程

(5)

由文献[1] 可知，方程(1)的非平凡解为

(6)

我们常用孤立子方程的守恒性质来检验对方程数值离散的精度[13] 。一个具体的孤立子波的能量表达式为

(7)

2. 紧致有限体积方法

考虑计算区域为，将其剖分成个区域，那么共有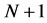个结点，每个小区间的长度为

对(1)式在第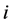个小区间单元上对上式求积分，并对等式两边同时除以，可以得到

(8)

记，称为在第个单元上的单元平均值，那么(8)式可以简记为

首先，要对上式、进行估计，通过参考文献我们可以得到如下的估计式

(9)

对应4阶精度的系数为[14]

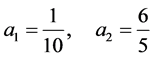
这些系数的确定，可以通过在点泰勒展开得到，例如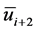在点的泰勒展开为

并且在Sine-Gordon方程中对应的边界条件为Dirichlet边界条件，那么对应的左边界处格式为

(10)

通过Taylor展开计算出对应的系数为

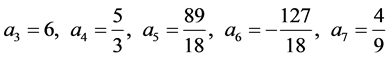
相应的右边界格式只是左边界格式的一个镜面映射。令

那么可以得到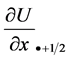和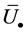之间的关系如下

(11)

,

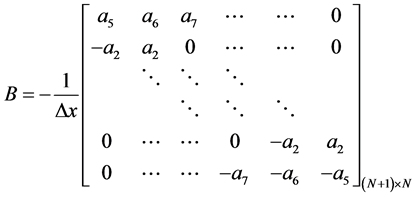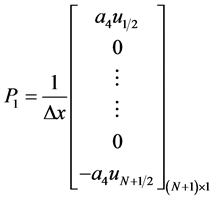
这样，我们就可以得到关于一阶导数离散格式为

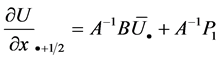(12)

对于右端项的非线性项，我们选取了常用的辛普森公式近似计算其定积分

(13)

此时仍需要对上式中的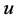利用单元平均值进行近似。对于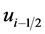和可以利用下面的格式近似

(14)

其中4阶格式的相应系数为[14]

对于Dirichlet边界条件，该格式也可以直接应用。下面令

那么在对于空间离散的过程中，可以得到和之间的关系，如下

, ,

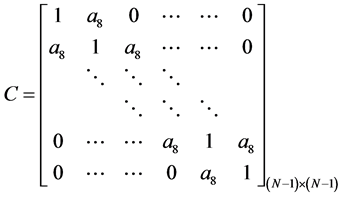得到空间离散格式为

(15)

这样就将数值积分中的单元边界值处理完毕。下面要解决在点的数值近似，其中一种方法就是利用上文已经处理的单元边界值对其进行近似，从而得到一个4阶数值近似格式

(16)

对应的Dirichlet边界条件的左边界格式为

(17)

对应的系数为

右边界也是类似的格式。我们令

那么可以得到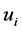和之间的关系，如下

,

这样就可以得到空间离散格式为

(18)

将整个离散后的右端项记为，就有，这是一个常微分方程，从而空间离散完成。

3. Runge-Kutta时间离散

在将右端项进行空间半离散之后，再考虑初始条件和边界条件，用3阶强稳定Runge-Kutta (a third- order strong stability preserving Runge-Kutta，即SSP-RK3)方法进行下一步处理。3阶的SSP-RK3的一般形式为[15]

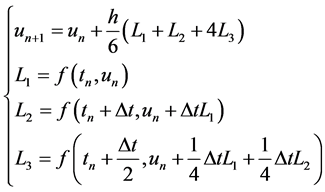(19)

对于Sine-Gordon方程，需要将其转换成一阶常微分方程组，再用Runge-Kutta方法进行时间离散。如下

R，P分别定义为空间上的线性和非线性的微分算符。时间格式的选取依赖于所要的精度阶，要考虑储存、计算、稳定性。尤其是当R，P是非线性的时候，更没有依据说明全离散后的格式是稳定的，这时就更需要强稳定时间格式，常见的高阶稳定离散可见[16] 。

2阶方程对应初值问题的一般形式为

引进变量，可化为1阶方程组的初值问题

(20)

(20)式对应的Runge-Kutta格式为

(21)

4. 数值算例

例1：考虑如下的一维sine-Gordon方程

(22)

将其改写为1阶方程组

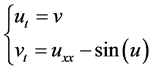
该方程的精确解为 [17]

通过下列的范数定义来计算所得的格式误差收敛阶，记

精度阶计算公式为

在区间[−6,6]上求解方程(22)，取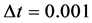，， (见表1)。图1为在的时候精确解和数值解的曲线拟合情况。可以看到在不同的范数意义下，阶数都达到了4阶左右，从图像和误差上，都能看出准确解和数值解有着较好的吻合程度。

例2：一维sine-Gordon方程

(23)

精确解为

表1. 4阶紧致有限体积方法下的误差和精度阶

图1. 例1数值解和精确解的比较

表2. 4阶紧致有限体积方法下的误差和精度阶

图2. 例2数值解和精确解的曲线拟合

在区间[−6,6]上求解方程(24)，取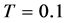， (见表2)，在的时候精确解和数值解的曲线拟合情况(如图2)。从图像和误差上，准确解和数值解有着较好的吻合程度。因为初值条件相对于例1较为简单，从而在误差和精度阶上有着更好的结果。

基金项目

本文由教育部科学技术研究重点项目(12024)，内蒙古自治区人才开发基金项目(12000-1300020240)和内蒙古自然科学基金(2015MS0101)支持。

文章引用

刘盎然,高巍,李宏. 一维Sine-Gordon方程四阶紧致有限体积方法
A Fourth-Order Compact Finite Volume Scheme for 1D Sine-Gordon Equations[J]. 应用数学进展, 2015, 04(03): 262-270. http://dx.doi.org/10.12677/AAM.2015.43032

参考文献 (References)