Advances in Applied Mathematics
Vol.04 No.04(2015), Article ID:16365,14
pages
10.12677/AAM.2015.44043
A New Difference Scheme and Convergence Criterion for Gradient Optimization Method for Slope Stability
Mengxi Wu1, Fanmin He1, Zhenggang Zhan2, Fuping Fan2
1Institute of Mechanics, Chinese Academy of Sciences, Beijing
2Powerchina Guiyang Engineering Limited, Guiyang Guizhou
Received: Oct. 29th, 2015; accepted: Nov. 14th, 2015; published: Nov. 19th, 2015
Copyright © 2015 by authors and Hans Publishers Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/



ABSTRACT
It is necessary to use optimization methods to find the most dangerous sliding surface for the safety factor of slope stability calculated by the limit equilibrium method. Gradient method is an accurate optimization method, however there may fail to find accurately the most dangerous sliding surface. An improved gradient optimization method with a descent difference scheme for the calculation of the direction vector is proposed. The descent difference scheme is superior to the central difference scheme both in accuracy and consuming time. The problem of wrong search direction occurring in the central difference scheme is dissolved in this scheme. The problem of convergence criterion used in the classical optimization method based on the gradient of the objective function is pointed out. A new convergence criterion for single variable optimization or for multivariable optimization along the gradient direction is proposed. The stability of three test examples is analyzed with a two-stage search method for circular slip surface. The gradient method combined with the descent difference scheme is an accurate and efficient method with an ability of avoiding to fall to a local minimum in a search process. The errors of search results in the test examples are less than the given convergence error. The proposed convergence criterion is appropriate.
Keywords:Slope Stability, Difference Scheme, Convergence Criterion, Optimization Method

边坡稳定梯度法优化计算中新的差分格式与收敛准则
吴梦喜1,何蕃民1,湛正刚2,范福平2
1中国科学院力学研究所,北京
2中国电建集团贵阳勘测设计研究院,贵州 贵阳

收稿日期:2015年10月29日;录用日期:2015年11月14日;发布日期:2015年11月19日

摘 要
用极限平衡方法计算边坡稳定的安全系数,需要采用优化方法寻找最危险滑裂面。梯度法是一种精确的优化方法方法,然而在边坡稳定分析中存在不能准确找到最危险滑裂面的问题。改进了梯度优化方法,提出了优化方向向量的下降差分格式。它解决了采用中心差分格式出现的搜索方向错误的问题,在有效性、计算精度和优化时间方面都优于中心差分格式。指出了传统梯度优化方法中忽视收敛标准的问题,并提出了一个单变量或多变量沿着优化方向进行优化搜索时的收敛准则。采用2阶段圆弧滑动面搜索方法,对3个测试算例的安全系数进行了下降差分格式和中心差分格式优化搜索的对比,表明改进的梯度法结合下降差分格式是能跳出局部极值的精确有效的方法。算例中采用下降差分格式搜索结果的误差均小于给定误差标准,表明所提出的收敛准则是合适的。
关键词 :边坡稳定,差分格式,收敛准则,优化方法

1. 介绍
土质边坡的稳定性分析是岩土工程中的基本问题之一。极限平衡法是一个评估给定滑动面安全性的有力方法。按照计算沿着滑动面安全系数方法的不同分成两类:基于条分法的常规极限平衡法和基于有限元应力场计算的改进极限平衡法[1] -[4] 。常规极限平衡法因其简单得到了广泛应用。其主要不足是需要假定条间力的作用位置或方向。改进的极限平衡法有获得可靠应力的声誉,因而在精度上优于常规方法。
边坡稳定安全分析中需要采用优化技术确定临界滑动面。优化技术发展了40年,已经有确定滑动面形状和位置的不同方法。优化方法一般可以分为确定性的和启发式的2个基本类型。确定性方法 [5] - [9] 基于目标函数的梯度信息和约束,有可能由于局部极值的出现找到一个伪的临界滑动面 [8] [10] [11] 。启发式方法包括遗传算法、模拟退火、禁忌搜索、蚁群优化、粒子群优化等多种方法,使用随机技术且包括从一个解移动到另一个解的随机性,快速容易地找到解答,但不保证找到的解答是最优解;因此可以认为是近似的非精确的方法 [12] 。确定性方法中计算目标函数的梯度方向是必不可少的。人们普遍认识到向前向后差分格式都不适合于梯度方向的计算,因为采用这些差分格式获得的梯度方向可能会大大偏离目标函数的实际梯度方向,甚至处于反方向,因而一般采用中心差分法计算梯度方向 [13] [14] 。然而,本文研究显示中心差分法获得的向量在极值附近仍然可能不是下降方向,因而精确的最小值位置仍然不能找到。另外,虽然收敛准则在确定极值时是很重要的,遗憾的是在此方面却少有学者探讨。
本文改进了边坡稳定的梯度方法,提出了下降差分格式和新的收敛准则。
2. 改进的边坡稳定分析梯度优化方法
以寻找土质边坡圆弧滑动临界滑动面为例,来说明优化方法及其改进。
2.1. 基于目标函数梯度的改进优化方法
寻找具有最小稳定安全系数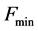 的临界滑动面,是一个将由一组几何变量
的临界滑动面,是一个将由一组几何变量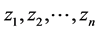 组成的向量
组成的向量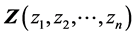 所定义的滑动面的安全系数
所定义的滑动面的安全系数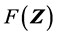 最小化的过程。这个过程从一个初始滑弧动面
最小化的过程。这个过程从一个初始滑弧动面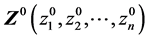 开始搜索直到找到具有最小安全系数
开始搜索直到找到具有最小安全系数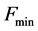 的滑动面为止。初始滑动面的不同将不会影响搜索结果,除非存在多级值问题。临界滑动面位于向量Z的边界或安全系数梯度向量G等于0的位置。
的滑动面为止。初始滑动面的不同将不会影响搜索结果,除非存在多级值问题。临界滑动面位于向量Z的边界或安全系数梯度向量G等于0的位置。
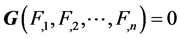 (1)
(1)
变量的上标表示搜索步。在m步搜索时,如下式所示,按照下降方向向量S和步长系数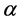 ,将滑动面位置从
,将滑动面位置从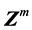 移向一个期望具有较小安全系数的新位置
移向一个期望具有较小安全系数的新位置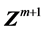
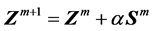 (2)
(2)
最速下降法定义方向向量 为梯度向量
为梯度向量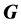 的负方向,即:
的负方向,即:
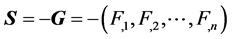 (3)
(3)
传统方法通过求解如下所示的单变量优化方程找到沿着梯度方向使目标函数为最小的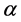 值。
值。
 (4)
(4)
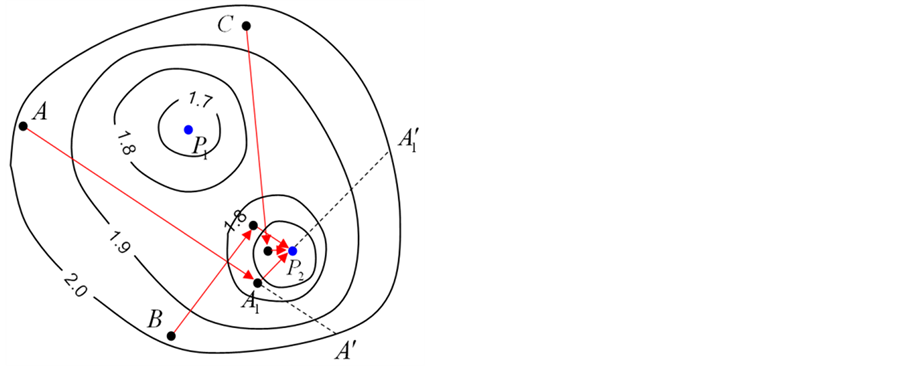
如图1(a)所示,从三个初始点A、B、C出发,用传统方法搜索目标函数的最小值。搜索从初始点A开始,沿着A点的最速下降方向AA'移动到该线上的最小点A1。重复这一过程直到找到最小值点P2。同样地,从B、C出发也找到P2。不幸的是另一个极值点P1没有被发现。
 (a) (b)
(a) (b)
Figure 1. Sketch of steepest descent search (a) traditional methods; (b) improved methods
图1. 最速下降法搜索(a) 传统方法;(b) 改进方法
如果式(4)直接采用一个固定的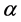 值,如图1(b)所示,近似地沿着最速下降方向小步长前进,使目标函数稳步降低。如果目标函数值在试探位置没有减小,即
值,如图1(b)所示,近似地沿着最速下降方向小步长前进,使目标函数稳步降低。如果目标函数值在试探位置没有减小,即 ,则目标函数从
,则目标函数从 到
到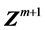 这个步长空间里一定经历了一个先下降后上升的过程,说明
这个步长空间里一定经历了一个先下降后上升的过程,说明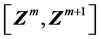 存在一个沿着这两点连线的极小值。采用单变量优化方法可确定这一极值点的位置并将其作为下一步搜索的起点。极值点P1和P2在这一改进的方法中都找到了。改进的搜索方法搜索点近似地按照最速下降方向前进,是一个真正的“下山法”。从一系列搜索路径中可以得到目标函数的等高线信息,从而判断搜索到的极小值的全局属性。
存在一个沿着这两点连线的极小值。采用单变量优化方法可确定这一极值点的位置并将其作为下一步搜索的起点。极值点P1和P2在这一改进的方法中都找到了。改进的搜索方法搜索点近似地按照最速下降方向前进,是一个真正的“下山法”。从一系列搜索路径中可以得到目标函数的等高线信息,从而判断搜索到的极小值的全局属性。
将滑弧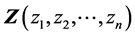 中各变量的定义域都归一化到[0, 1],且当方向向量不等于0时将其进行归一化可以使自变量的范围和移动步长的选取不受边坡的几何尺寸影响。当方向向量等于0时,极值存在于这一点的邻域内。依据几何条件确定的变量
中各变量的定义域都归一化到[0, 1],且当方向向量不等于0时将其进行归一化可以使自变量的范围和移动步长的选取不受边坡的几何尺寸影响。当方向向量等于0时,极值存在于这一点的邻域内。依据几何条件确定的变量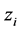 的定义域为
的定义域为 ,归一化公式为
,归一化公式为
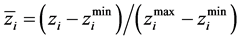 (5)
(5)
基于当前位置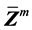 按照下式计算试探滑动面位置向量
按照下式计算试探滑动面位置向量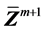
 (6)
(6)
其中 是归一化后的方向向量,
是归一化后的方向向量,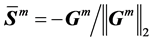 ,
,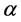 是一个远远小于1的系数,其取值应使其沿着不同初始点出发的搜索能够如“下山”一样,能找出低洼点。对于边坡稳定优化一般可取0.1,而对于极值很多的情况,可取更小的步长。
是一个远远小于1的系数,其取值应使其沿着不同初始点出发的搜索能够如“下山”一样,能找出低洼点。对于边坡稳定优化一般可取0.1,而对于极值很多的情况,可取更小的步长。
2.2. 目标函数梯度方向计算的下降差分格式
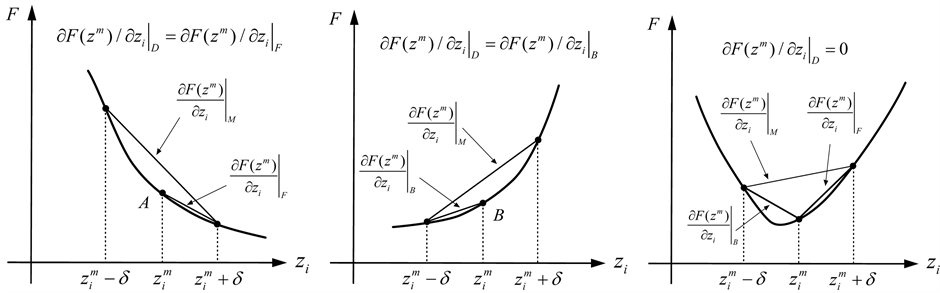
一般认为向前差分和向后差分都不适合于方向向量的计算,因为按照这两种差分格式计算,极值点附近的方向向量可能与实际情况相反(朱伯芳等,1984;陈祖煜,2003)。中心差分法被广泛用于搜索向量的计算。然而,中心差分计算所得的方向向量只有在目标函数沿着坐标轴方向在计算点前后一个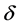 差分步长内线性变化才是准确的。目标函数在其等值线形成一个沟或在极小值存在的凹陷处的变化是非线性的,计算所得的方向向量大大偏离最速下降方向,也很难得到0值。搜索终止于一个近似的极值点位置,甚至终止于一个伪极值点位置。为了解决这一问题,本文提出如图2所示的下降差分格式。图2中
差分步长内线性变化才是准确的。目标函数在其等值线形成一个沟或在极小值存在的凹陷处的变化是非线性的,计算所得的方向向量大大偏离最速下降方向,也很难得到0值。搜索终止于一个近似的极值点位置,甚至终止于一个伪极值点位置。为了解决这一问题,本文提出如图2所示的下降差分格式。图2中
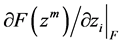 、
、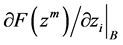 、
、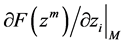 分别表示向前差分、向后差分、中心差分,其值等于图中箭头所指的线段的斜率。
分别表示向前差分、向后差分、中心差分,其值等于图中箭头所指的线段的斜率。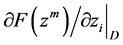 为下降差分,其值在情况(a)等于向前差分值;在情况(b)等于向后
为下降差分,其值在情况(a)等于向前差分值;在情况(b)等于向后
差分值;在情况(c)等于0。显然,与中心差分法比较,下降差分法所得的方向向量在目标函数如图2(a)和图2(b)这种在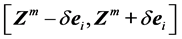 区间为单调的情况下更准确,其中
区间为单调的情况下更准确,其中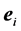 为坐标轴
为坐标轴 方向的单位向量,
方向的单位向量,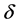 为差分步长。
为差分步长。
下降差分格式的计算公式如下:
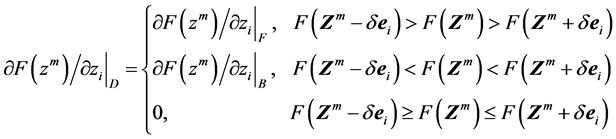 (7)
(7)
其中, 和
和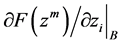 分别为向前和向后差分值,按照如下公式计算:
分别为向前和向后差分值,按照如下公式计算:
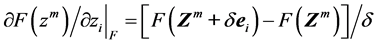 (8)
(8)
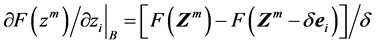 (9)
(9)
 (a) (b) (c)
(a) (b) (c)
Figure 2. Sketch of the descent difference scheme (a) descent forward; (b) descent backward; (c) descent neither forward nor backward
图2. 下降差分格式(a) 向前下降;(b) 向后下降;(c) 非向前向后下降
 点目标函数沿着坐标轴i的差分计算从下降方向的一个猜测开始。上一步的下降方向可以作为一个猜测。猜测的下降方向是向前时计算
点目标函数沿着坐标轴i的差分计算从下降方向的一个猜测开始。上一步的下降方向可以作为一个猜测。猜测的下降方向是向前时计算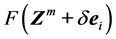 ,向后时计算
,向后时计算 。然后将计算值与已获得的
。然后将计算值与已获得的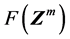 比较,检验猜测方向是否正确。如果猜测正确,则可计算出差分值,否则计算
比较,检验猜测方向是否正确。如果猜测正确,则可计算出差分值,否则计算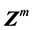 坐标轴另一侧差分点的安全系数值,按照式(7)计算出差分值。这种差分格式的安全系数计算次数介于
坐标轴另一侧差分点的安全系数值,按照式(7)计算出差分值。这种差分格式的安全系数计算次数介于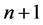 与
与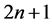 之间,而中心差分格式的计算次数为
之间,而中心差分格式的计算次数为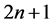 。
。
按照下降差分格式,如果方向向量为0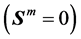 ,则
,则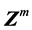 的近似
的近似 邻域内存在极值点。在区间
邻域内存在极值点。在区间 内,沿着坐标轴方向,对变量
内,沿着坐标轴方向,对变量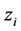 ,
,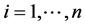 ,进行一维优化得到这个方向的极小点,并更新
,进行一维优化得到这个方向的极小点,并更新 进行下一个坐标轴方向的一维优化,直到n个坐标轴方向优化所得的结果小于收敛误差为止。虽然理论上除了边界以外,最小值只存在于梯度向量G等于0的部位。然而由于中心差分法的计算误差,真实的偏导数等于0的部位其导数计算值却与0有一定的误差,而这一误差范围也很难界定。因此,用中心差分法计算很难用梯度向量等于0作为极值点位置的判断。
进行下一个坐标轴方向的一维优化,直到n个坐标轴方向优化所得的结果小于收敛误差为止。虽然理论上除了边界以外,最小值只存在于梯度向量G等于0的部位。然而由于中心差分法的计算误差,真实的偏导数等于0的部位其导数计算值却与0有一定的误差,而这一误差范围也很难界定。因此,用中心差分法计算很难用梯度向量等于0作为极值点位置的判断。
为了防止搜索停止于局部小坑,将沿坐标轴优化的区间扩大到 (
(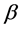 等于
等于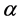 常常是一个好选择),如果某一坐标轴上的极值点位于
常常是一个好选择),如果某一坐标轴上的极值点位于 之外,则
之外,则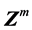 点
点 邻域内的极小点为局部极值,以邻域外的这个极小点作为新的搜索起点继续搜索过程,可实现搜索过程不受局部小坑影响的功能。
邻域内的极小点为局部极值,以邻域外的这个极小点作为新的搜索起点继续搜索过程,可实现搜索过程不受局部小坑影响的功能。
差分步长 的取值一般应较小,使计算所得的梯度方向向量与优化变量当前点处的实际梯度方向接近。一般可取0.01,当移动步长
的取值一般应较小,使计算所得的梯度方向向量与优化变量当前点处的实际梯度方向接近。一般可取0.01,当移动步长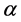 小于0.01时,应取差分步长等于移动步长。
小于0.01时,应取差分步长等于移动步长。
2.3. 收敛准则
收敛条件的设定是优化问题的一个基础。单变量优化的终止需要一个收敛准则。传统方法中搜索终止条件 [8] 为
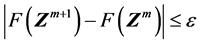 (10)
(10)
其中ε取一个小值,如1.5 × 10−5。如图3所示,实际安全系数与最小值的偏差可能远远大于给定的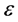 值,
值,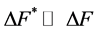 。
。
对于目标函数(连续)的最小值存在于单值区间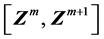 之中的单变量优化问题,在搜索点从两侧向极值点
之中的单变量优化问题,在搜索点从两侧向极值点 移动的过程中目标函数的梯度是非增加的,即
移动的过程中目标函数的梯度是非增加的,即

Figure 3. Comparison of the true error with the difference of the two consecutive iterations
图3. 相邻两次迭代值之差与实际误差的比较
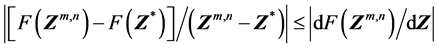 (11)
(11)
黄金分割法或二分法等的搜索过程中, 总是在
总是在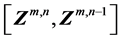 区间中,因此
区间中,因此
 (12)
(12)
将式(12)代入式(11)可得
 (13)
(13)
满足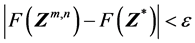 的充分条件是
的充分条件是
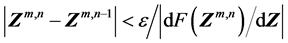 (14)
(14)
式(14)是单变量优化或多变量中沿着一条直线优化的收敛准则。
2.4. 圆弧滑动面优化变量
土质边坡的滑动破坏面在大多情况下近似为圆弧。因此,边坡稳定分析时对任意给定的圆弧计算安全系数,寻找安全系数最小的圆弧即圆弧滑动面优化。
平面上圆的确定需要圆心的两个坐标值和半径三个参数。以往多选用滑动面的圆心坐标和半径作为优化参数,但存在圆心坐标和半径的取值范围大,边界位置难以确定等困难。对于表面形状复杂的边坡,一个圆与边坡相交的弧段可能还不止一个。因此,优化变量采用圆心坐标和半径存在问题。将滑动面与坡面的2个交点--滑入点和滑出点的某一坐标(x坐标或y坐标)和拱高作为控制变量的方法解决了这一问题 [15] 。然而,对于坡面存在垂直段(采用x坐标)或水平段(采用y坐标)的情况,不能唯一确定圆弧。将此方法做一微小改进,即建立沿着坡面的一维曲线坐标,即可解决问题。因此,本文采用的圆弧滑动面控制变量是滑入点和滑出点的一维坐标和拱高。
如图4所示,在边坡上取一点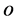 为原点,建立沿着边坡上表面的一维曲线坐标系。圆弧以滑入点
为原点,建立沿着边坡上表面的一维曲线坐标系。圆弧以滑入点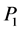 、滑出点
、滑出点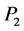 的一维坐标
的一维坐标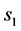 、
、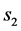 和拱高
和拱高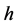 为控制变量。滑动面可以用向量
为控制变量。滑动面可以用向量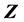 表达
表达
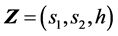 (15)
(15)
根据需要搜索的圆弧滑动面滑入滑出点的范围和边坡上下表面对圆弧的约束,可得到各控制变量的取值范围分别为

Figure 4. Variables defining a circular slip surface
图4. 圆弧滑动面的控制变量定义
 (16)
(16)
式中, 、
、 和
和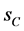 、
、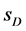 分别为滑入滑出点范围的端点
分别为滑入滑出点范围的端点 、
、 、
、 、
、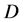 的一维坐标;
的一维坐标;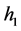 为通过滑入点
为通过滑入点 和滑出点
和滑出点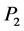 的滑动面最小拱高,
的滑动面最小拱高,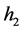 为圆弧与边坡边界相切时滑动面的拱高,
为圆弧与边坡边界相切时滑动面的拱高,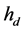 定义为滑动面的深度,
定义为滑动面的深度,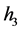 为拱高与滑动面深度之差,
为拱高与滑动面深度之差, 为设定的最小滑动面深度。
为设定的最小滑动面深度。
对各变量进行无量纲归一化处理,有
 (17)
(17)
滑入滑出点的坐标归一化后取值范围为[0, 1],拱高归一化后取值范围为(0, 1]。
2.5. 圆弧滑动面的两级搜索方法
在圆弧型临界滑动面搜索过程中,一般采用是滑动面控制变量一起移动的搜索方法,本文将这种滑动面控制变量整体寻优的搜索方法称为“一级搜索方法”。采用这种搜索方式对简单边坡进行临界滑动面搜索时,易陷入局部极值 [14] 。张小稳等人提出了“两级搜索方法” [16] ,即:对于任意给定滑弧,首先对拱高进行优化,最给定滑入滑出点位置条件下的最小安全系数滑弧。因此,经过拱高优化后,优化变量减少一个,第二级优化是对滑入滑出点位置(s1, s2)的优化。
一般情况下,对于给定滑入点和滑出点的一组滑弧,安全系数与拱高的关系曲线并不是一个单峰曲线,如图5所示。因而可首先采用枚举法,将曲线分成若干单极值区间。然后再采用黄金分割法求单峰区间的极值,并和区间的端点比较,取得全局的最小值。本文通过将拱高的变化区间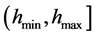 等份为若干份(50份),依变量从小到大计算各点安全系数。安全系数的峰值点,即为区间的分割点。如图5所示的拱高区间
等份为若干份(50份),依变量从小到大计算各点安全系数。安全系数的峰值点,即为区间的分割点。如图5所示的拱高区间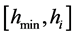 ,
,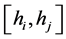 和
和 均为单极值(最小值)区间。对于每个单峰值区间采用一维寻优方法找到极小值点,可求得到区间
均为单极值(最小值)区间。对于每个单峰值区间采用一维寻优方法找到极小值点,可求得到区间 内的最小安全系数拱高
内的最小安全系数拱高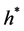 。
。
对拱高进行一级优化后,边坡圆弧滑动的优化函数可表示为
 (18)
(18)
上式是对滑入滑出点为优化变量,对于每一组滑入滑出点,首先找到最小安全系数拱高,然后寻找整体最小安全系数滑弧的二步优化方法优化函数。
3. 基于圆弧滑动算例的方法验证
选用1987年澳大利亚计算机协会(ACADS)设计的10个标准测试问题中的三个,EX1a,EX1c和EX5c做为测试本文算法可行性的算例 [17] ,在本文中对应编号为TE1,TE2和TE3。分别为无渗流均质边坡(TE1)、无渗流非均质边坡(TE2)和有自由水面均质边坡(TE3)。文献 [17] 推荐的TE1,TE2和TE3安全系数参考答案分别为1.00、1.39、1.59。
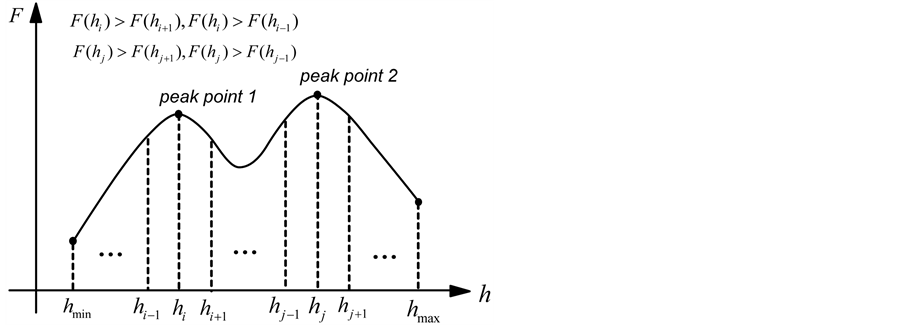
Figure 5. Determination of single peak intervals
图5. 单峰值区间的确定
3.1. 经典算例介绍
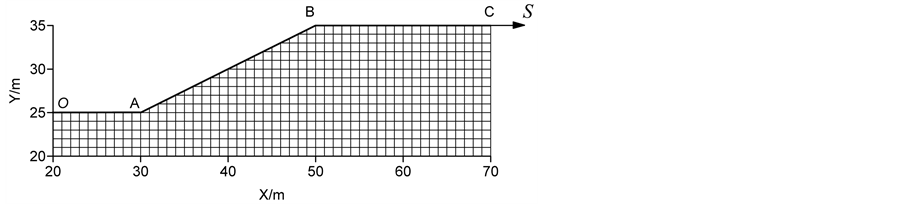
三个算例几何模型和网格见图6所示,其中TE1和TE2的几何模型相同,并且坡内无渗流;TE3为坡内有自由水面的均质边坡,左侧坡外基坑中水位高程为26.0 m,右侧水位为33.0 m。三个算例模型的网格尺寸均约为1.0 m。在图6中,多段线 和多段线
和多段线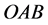 分别表示圆弧形滑动面滑入点和滑出点的变动区间。
分别表示圆弧形滑动面滑入点和滑出点的变动区间。
土层材料采用线弹性模型,荷载一次施加,采用有限元计算获得TE1的竖直方向正应力如图7所示,竖直方向正应力大小基本与土层的埋深成正比。由于TE2中土体的容重,与TE1的相差不大,且两个算例中土体的弹性模量和泊松比均相同,因此,采用线弹性模型计算的TE2的应力结果和TE1基本类似。
计算得到TE3稳定渗流情况下的边坡孔隙水压力以及相应的竖向有效正应力等值线分别见图8、图9。
3.2. 下降差分格式有效性验证
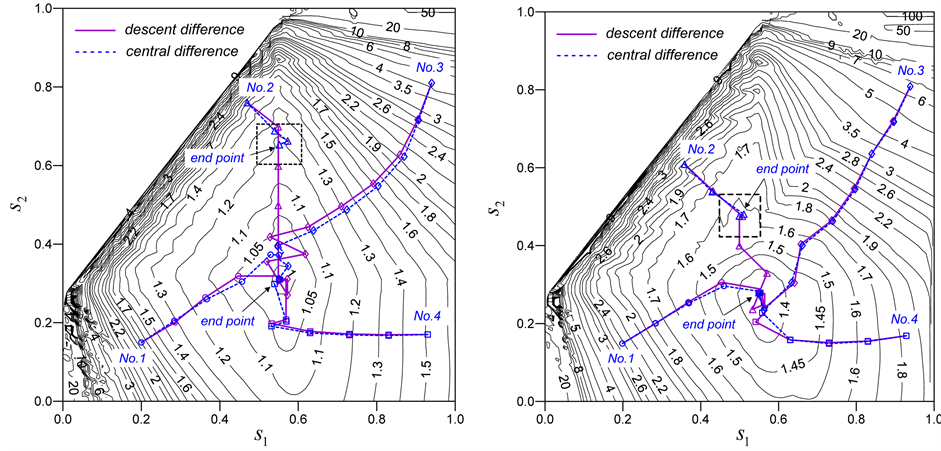
对于优化变量范围均为[0, 1]的优化问题,选择一系列均匀分布的初始滑弧是很容易的。各算例分别采用中心差分格式和下降差分格式,选取了4个初始优化点进行优化,其优化轨迹如图10所示。差分步长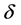 取0.01,移动步长
取0.01,移动步长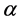 取0.1,收敛误差标准取0.001。由于基于有限元应力结果计算滑弧安全系数时,只需要通过插值即可获得滑弧上的应力,因而与基于条分法的常规极限平衡法相比,搜索过程费时很短。一个搜索路径的计算时间在普通台式机上(主频2.66 GH,内存3.50 GB)小于3 s。图中的安全系数等值线图是根据滑入滑出点归一化坐标
取0.1,收敛误差标准取0.001。由于基于有限元应力结果计算滑弧安全系数时,只需要通过插值即可获得滑弧上的应力,因而与基于条分法的常规极限平衡法相比,搜索过程费时很短。一个搜索路径的计算时间在普通台式机上(主频2.66 GH,内存3.50 GB)小于3 s。图中的安全系数等值线图是根据滑入滑出点归一化坐标 和
和 按0.01间隔取所有点,通过一维优化基于获得每个点的最小安全系数而绘制的。这些等直线给出了边坡圆弧滑动安全系数的整个信息,是为了帮助理解搜索有效性和效率而单独计算给出的,搜索过程独立于此。采用下降差分格式计算的4个搜索的终点在3个算例中都几乎重合,安全系数分别是0.987,1.365和1.539,与参考答案的比较见表4。而采用中心差分格式计算的No. 2搜索在TE1和TE2中都与其他搜索终止于不同点。其原因将在下节讨论。
按0.01间隔取所有点,通过一维优化基于获得每个点的最小安全系数而绘制的。这些等直线给出了边坡圆弧滑动安全系数的整个信息,是为了帮助理解搜索有效性和效率而单独计算给出的,搜索过程独立于此。采用下降差分格式计算的4个搜索的终点在3个算例中都几乎重合,安全系数分别是0.987,1.365和1.539,与参考答案的比较见表4。而采用中心差分格式计算的No. 2搜索在TE1和TE2中都与其他搜索终止于不同点。其原因将在下节讨论。
3.3. 两种差分格式搜索结果的比较
3个算例两种差分格式搜索结果的比较分别列于表5、表6和表7。下降差分格式不同搜索路径的终点和安全系数都比中心差分格式的结果更靠近。下降差分格式所得安全系数结果的最大差异在TE1、TE2
 (a)
(a)
 (b)
(b)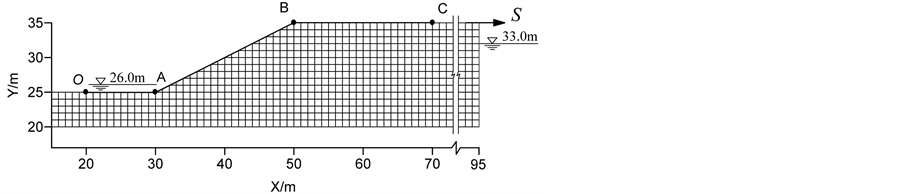 (c)
(c)
Figure 6. Configuration and mesh of the (a) TE1, (b) TE2 and (c) TE2
图6. 三个算例的几何模型和网格(a) TE1,(b) TE2和(c) TE3
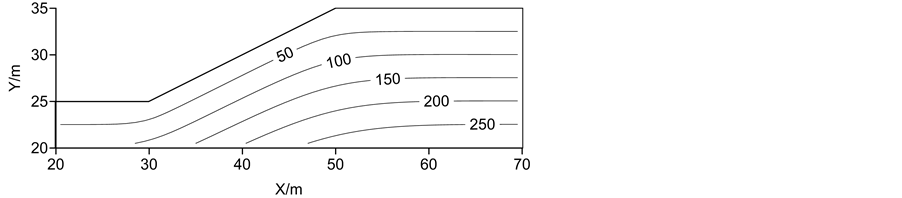
Figure 7. Contours of the vertical normal stress of TE1/kPa
图7. TE1的竖直方向正应力(kPa)

Figure 8. Contours of the pore water pressure of TE3/kPa
图8. TE3的孔隙水压力(kPa)
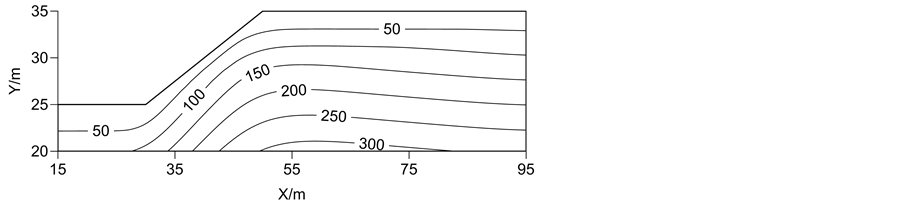
Figure 9. Contours of the vertical normal stress of TE3/kPa
图9. TE3的竖直方向有效正应力(kPa)
 (a) (b)
(a) (b)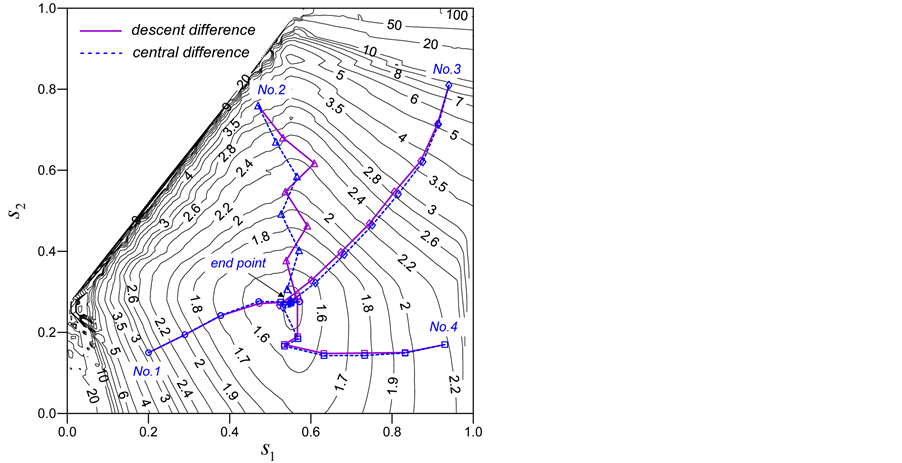 (c)
(c)
Figure 10. Search paths with several initial points for (a) TE1, (b) TE2 and TE3
图10. 算例(a) TE1,(b) TE2和TE3中几个起点的搜索路径
Table 1. Geotechnical parameters for TE1
表1. TE1土层的材料参数表
Table 2. Geotechnical parameters for TE2
表2. TE2土层的材料参数表
Table 3. Geotechnical parameters for TE3
表3. TE3土层的材料参数表
Table 4. Comparison of the factors of safety by this study and the reference answers
表4. 计算所得安全系数与参考答案的比较
Table 5. Comparison of the search results with the two difference schemes in TE1
表5. TE1中2种差分格式搜索结果的比较
Table 6. Comparison of the search results with the two difference schemes in TE2
表6. TE2中2种差分格式搜索结果的比较
和TE3中分别为0.0008,0.0001和0.0000。它们都低于设定的收敛误差0.001。中心差分格式的最大差异在TE1、TE2和TE3中分别为0.1936、0.2062和0.0003。TE1和TE2中分别是给定收敛误差的194和206倍,TE3中则低于收敛误差。
图10中两种差分格式的搜索路径在等值线顺直的部位差异小,而等值线弯曲的部位差异大。下降差分格式中搜索方向近似于等值线梯度方向,而中心差分格式在搜索起点在等值线形成沟谷处则与梯度方向差异很大。如图10(c)中No. 2搜索路径所示,中心差分计算的梯度方向与实际梯度方向误差很大。
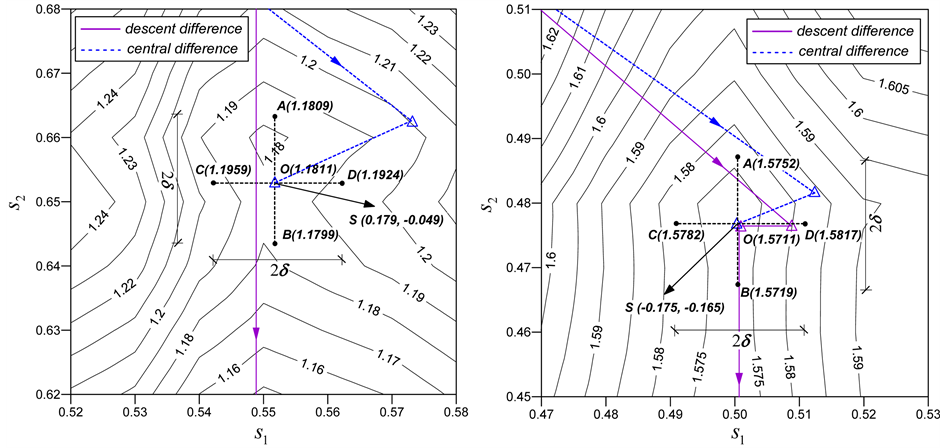
TE1和TE2中采用中心差分格式没有找到最小值的No. 2搜索路径终点的搜索信息如图11所示。两个例子中中心差分格式搜索落入一个等高线凹形区域O点,安全系数沿着中心差分格式计算出来的方向安全系数不下降。图中点A,B,C,D和O后面括号里的数字是这些点的安全系数。它们表明TE1中O点不是极值,TE2中O点靠近一个局部极值点。用下降差分格式的搜索路径在TE1中通过了O点附近区域,在TE2中在局部极值点跳出来了搜索得以继续。显然与下降差分格式结合的改进的梯度方法是精确的且有能力跳出局部极值,而与中心差分格式结合则不是精确的,甚至会陷入局部极值。
3.4. 收敛准则的验证
TE1、TE2、TE3几个收敛误差值下最小安全系数分别列于表8、表9和表10。不妨将 等于0.0001的最小计算结果当作真实值,表中括号内的数值为
等于0.0001的最小计算结果当作真实值,表中括号内的数值为 大于0.0001时的计算误差。不同搜索路径所得结果的误差均小于给定误差标准。表明所给的收敛准则是合适的。
大于0.0001时的计算误差。不同搜索路径所得结果的误差均小于给定误差标准。表明所给的收敛准则是合适的。
Table 7. Comparison of the search results with the two difference schemes in TE3
表7. TE3中2种差分格式搜索结果的比较
Table 8. Comparison of the minimum factors of safety under several convergence standards in TE1
表8. TE1中几个收敛标准下的安全系数最小值比较
Table 9. Comparison of the minimum factors of safety under several convergence standards in TE2
表9. TE2中几个收敛标准下的安全系数最小值比较
Table 10. Comparison of the minimum factors of safety under several convergence standards in TE3
表10. TE3中几个收敛标准下的安全系数最小值比较
 (a) (b)
(a) (b)
Figure 11. The search information in the dashed box in Figure 10 (a) and (b)
图11. (a) TE1和(b) TE1中No. 2路径中心差分法搜索信息
4. 总结和结论
提出了一个计算优化梯度方向的下降差分格式。它在有效性和效率方面均优于中心差分格式。中心差分格式中的错误的搜索方向问题在下降差分格式中消失了。指出了传统梯度优化方法中的收敛标准问题,并提出了一个单变量或多变量沿着优化方向进行优化搜索时的收敛准则。采用2阶段圆弧滑动面搜索方法,对3个测试算例的安全系数进行了计算分析,表明改进的梯度法结合下降差分格式是有能力跳出局部极值的精确有效的方法。算例中搜索结果的误差均小于给定误差标准,表明所提出的收敛准则是合适的。
基金项目
国家科技支撑计划课题“喀斯特山区水库建设与安全保障技术及示范,2014BAB03B04”。
文章引用
吴梦喜,何蕃民,湛正刚,范福平. 边坡稳定梯度法优化计算中新的差分格式与收敛准则
A New Difference Scheme and Convergence Criterion for Gradient Optimization Method for Slope Stability[J]. 应用数学进展, 2015, 04(04): 343-356. http://dx.doi.org/10.12677/AAM.2015.44043
参考文献 (References)
- 1. Naylor, D.L. (1982) Finite Elements and Slope Stability. In: Martins, J.B., Ed., Numerical Methods in Geomechanics, D. Reidel Publishing Company, Dordrecht, 229-244. http://dx.doi.org/10.1007/978-94-009-7895-9_10
- 2. Kim, J.Y. and Lee, S.R. (1997) An Improved Search Strategy for the Critical Slip Surface Using Finite Element Stress Fields. Compute and Geotech, 22, 295-313. http://dx.doi.org/10.1016/S0266-352X(97)00027-X
- 3. Farias, M.M. and Naylor, D.J. (1998) Safety Analysis Using Finite Elements. Computers and Georechnics, 22, 165- 181. http://dx.doi.org/10.1016/S0266-352X(98)00005-6
- 4. Fredlund, D.G. and Scoular, R.E.G. (1999) Using Limit Equilibrium in Finite Element Slope Stability Analysis. Proceedings of the International Symposium on Slope Stability Engineering, ISShikoku ’99, Matsuyama, 8-11 November 1999, 31-47.
- 5. Baker, R. and Garber, M. (1977) Variation Approach to Slope Stability. Proceeding 9th International Conference on Soil Mechanics and Foundation Engineering, 2, 9-12.
- 6. Celestion, T.B. and Duncan, J.M. (1981) Simplified Search for Non-Circular Slip Surface. Proceeding 10th International Conference on Soil Mechanics and Foundation Engineering, 3, 391-394.
- 7. Nguyen, V.U. (1985) Determination of Critical Slope Failure Surface. Journal of Geotechnical Engineering, ASCE, 111, 238- 250.
- 8. Chen, Z.Y. and Shao, C.M. (1988) Evaluation of Minimum Factor of Safety in Slope Stability Analysis. Canadian Geotechnical Journal, 25, 735-748. http://dx.doi.org/10.1139/t88-084
- 9. Bardet, J. and Kapuskar, M. (1989) A Simplex Analysis of Stability. Computers and Geotechnics, 8, 329-348. http://dx.doi.org/10.1016/0266-352X(89)90039-6
- 10. McCombie, P. and Wilkinson, P. (2002) The Use of the Simple Genetic Algorithm in Finding the Critical Factor of Safety in Slope Stability Analysis. Computers and Geo-technics, 29, 699-714. http://dx.doi.org/10.1016/S0266-352X(02)00027-7
- 11. Taha, M.R., Khajehzadeh, M. and EI-Shafie, A. (2010) Slope Stability Assessment Using Optimization Techniques: An Overview. Electronic Journal of Geotechnical Engi-neering, 15, 1901-1915.
- 12. Cheng, Y.M. and Lau, C.K. (2008) Slope Stability Analysis and Stabilization. Routledge, Cornwall.
- 13. 朱伯芳, 黎展眉, 张璧城. 结构优化设计原理与应用[M]. 北京: 水利电力出版社, 1984.
- 14. 陈祖煜. 土质边坡稳定分析: 原理、方法、程序[M]. 北京: 中国水利水电出版社, 2003.
- 15. 周圆冗, 李守巨, 刘迎曦, 等. 基于遗传算法边坡稳定分析临界滑移面的搜索[J]. 岩石力学与工程学报, 2005, 24(Supp. 1): 5226-5230.
- 16. 张小稳, 张晓芳, 李国英. 基于弦高控制变量的边坡稳定分析方法[J]. 水利水运工程学报, 2007, 10(4): 62-65.
- 17. Donald, I.B. and Giam, P. (1992) The ACADS Slope Stability Programs Review. 6th International Symposium on landslides, 3, 1665-1670.
