Advances in Applied Mathematics
Vol.06 No.01(2017), Article ID:19594,9
pages
10.12677/AAM.2017.61006
Shadowing Property of Continuous Maps in 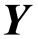 Space
Space
Yalin Tang1, Ridi Huang1, Chengbo Ye1, Gengrong Zhang1,2*
1School of Mathematics and Information Science, Guangxi University, Nanning Guangxi
2College of Mathematics and Computational Science, Hunan First Normal University, Changsha Hunan

Received: Jan. 1st, 2017; accepted: Jan. 17th, 2017; published: Jan. 22nd, 2017
Copyright © 2017 by authors and Hans Publishers Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/



ABSTRACT
The shadowing property study that whether or not arbitrary orbits of perturbation system (i.e. pseudo orbits of this system) exist actual orbits, which satisfy that error of single step between them is within the designated scope in the time synchronization. It has a close connection with the stability of a system, and plays a significant role in the qualitative theory of dynamical systems. This paper extends conclusion of Gedeon and Kuchta to prove the necessary and sufficient condition of the shadowing property of continuous maps in  space into itself.
space into itself.
Keywords: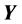 Space, Continuous Maps, Shadowing Property
Space, Continuous Maps, Shadowing Property

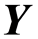 空间连续自映射的伪轨跟踪性
空间连续自映射的伪轨跟踪性
唐亚林1,黄日娣1,叶成博1,张更容1,2*
1广西大学,数学与信息科学学院,广西 南宁
2湖南第一师范学院 数学与计算科学学院,湖南 长沙

收稿日期:2017年1月1日;录用日期:2017年1月17日;发布日期:2017年1月22日

摘 要
伪轨跟踪性研究的是一个系统中任意扰动系统的轨道(即该系统的轨道)是否存在真正轨道使得在时间同步的意义下该轨道与伪轨的单步误差在指定范围内。它与系统的稳定性有着密切的联系,在动力系统的定性理论中起着重要的作用。本文扩展Gedeon和Kuchta的结论给出了 空间的连续自映射具有伪轨跟踪性的充分必要条件。
空间的连续自映射具有伪轨跟踪性的充分必要条件。
关键词 : 空间,连续自映射,伪轨跟踪性
空间,连续自映射,伪轨跟踪性

1. 引言
1992年,Gedeon和Kuchta证明了区间上连续自映射具有伪轨跟踪行的充分必要条件。到目前为止,已有学者研究伪轨跟踪性本身的若干性质,以及伪轨跟踪性与动力系统其他性质之间的关系 [1] 。本文将在这些结论的基础上结合近年来一些学者对树上连续自映射的Sarkovskii定理,Baldwin定理以及Li-Yorke混沌等性质的研究 [2] ,扩展文献 [3] 的结论到 空间。
空间。
2. 预备知识
设 ,称任意一个与集合
,称任意一个与集合 (
(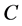 表示复数集合)同胚的树为
表示复数集合)同胚的树为 星,记为
星,记为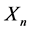 。当
。当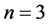 时,称与
时,称与 同胚的树为
同胚的树为 星,记为
星,记为 。设
。设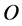 为
为 的分支点,记
的分支点,记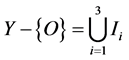 ,称
,称 为
为 的分支。
的分支。
对 的任一子集
的任一子集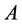 ,用
,用 表示
表示 上包含
上包含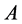 的最小子树。对于任意的
的最小子树。对于任意的 ,用
,用 表示
表示 ,记
,记 ,
, 。若
。若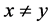 ,用
,用 表示
表示 含
含 的连通分支。
的连通分支。 上的度量
上的度量 定义为:对任意
定义为:对任意 ,
, 表示
表示 的长度。
的长度。
设 (
( 表示
表示 的端点),若
的端点),若 且
且 ,我们称
,我们称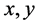 满足偏序关系
满足偏序关系 ,记作
,记作 。
。
设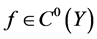 ,记
,记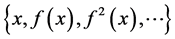 为
为 的轨道。记
的轨道。记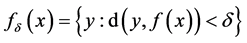 。
。
任给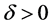 ,
, 的
的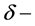 链或者
链或者 的
的 伪轨为序列
伪轨为序列 ,其中
,其中 。记
。记 表示
表示 的周期点集,
的周期点集, 表示
表示 的不动点集。
的不动点集。
若 且存在一个同胚映射
且存在一个同胚映射 ,其中
,其中 为
为 或
或 ,称
,称 为一个区间。
为一个区间。
若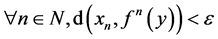 ,我们称
,我们称 链
链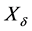 被
被 的轨道
的轨道 跟踪。
跟踪。
若 任意
任意 链
链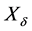 都可被某个
都可被某个 的轨道
的轨道 跟踪,则称
跟踪,则称 具有伪轨跟踪性。
具有伪轨跟踪性。
在本文中我们假设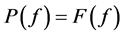 且
且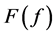 无处稠密。
无处稠密。
引理1 设 (
( 表示树),则下列条件等价:
表示树),则下列条件等价:
1) 对任意 收敛;
收敛;
2) ;
;
3) 若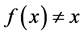 ,则对任意
,则对任意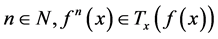 。
。
证明详情请见孙太祥等 [4] 编著的《树映射的动力学》引理2.1。□
引理2 设 且
且 。任取
。任取 ,若
,若 ,则对任意
,则对任意 ,我们有
,我们有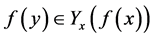 。
。
证明:若 。
。
 ,
, 。
。
不妨设 ,由
,由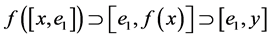 ,
,
 。
。
由引理1的(3)得 ,
, ,
,
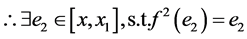 ,即
,即 。
。
由 ,
, ,与
,与 矛盾。□
矛盾。□
引理3 设 且
且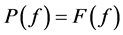 。任取
。任取 。任取
。任取 ,若
,若 ,则
,则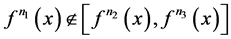 。
。
证明: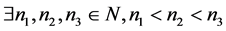 ,
, ,若
,若 ,
,
则 。
。
令 ,
, 。
。
显然 ,由引理1知对任意
,由引理1知对任意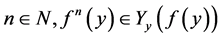 。
。
若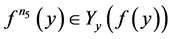 ,则
,则 ,与引理1矛盾;
,与引理1矛盾;
若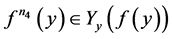 ,则
,则 ,与引理1矛盾。□
,与引理1矛盾。□
引理4 设 且
且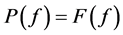 。任取
。任取 ,任取
,任取 ,其中
,其中 。
。
证明:由引理1知:对任意 ,
, 收敛。不妨设
收敛。不妨设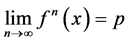 ,根据
,根据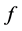 的连续性以及极限的唯一性得,
的连续性以及极限的唯一性得, 。□
。□
引理5 设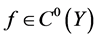 且
且 。对任意的
。对任意的
任意取 ,且
,且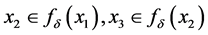 ,则我们有
,则我们有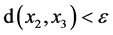 。
。
证明:
设 ,
, ,
,
显然 时,
时, 。
。
下面分两种情况讨论:
(A) 若 ,则
,则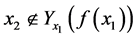 。
。
(A1) ;
;
(A2) ,
,
 ,
,
 。
。
(B) 若 ,则
,则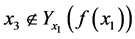 。
。
(B1)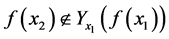 ,由引理2的逆否命题得
,由引理2的逆否命题得 ,
,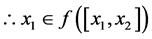 ,故
,故 。由引理2知
。由引理2知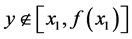 。
。
又 ,
,
 ,
, 。又
。又 ,从而
,从而 ,
, ,
,
 ,
,
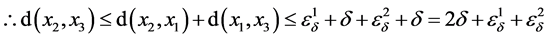 。
。
(B2) 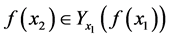
 ,
,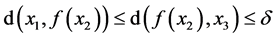 ,
,
又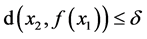 ,
, ,从而
,从而 。
。
综上所述, ,由
,由 时,
时, ,
, ,故
,故 。□
。□
引理6 设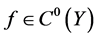 且
且 。设
。设 为
为 的端点,
的端点, 为
为 的分支点,其中
的分支点,其中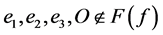 。设
。设 ,
,
 ,
,
 ,
,
 ,
,
令

 ,
,
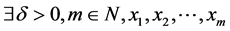 为
为 循环(
循环(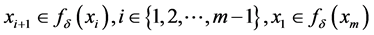 )
)
那么, (i.e.
(i.e. 足够小时,所有的
足够小时,所有的 循环都在区间
循环都在区间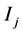 内)。
内)。
证明:设 (
( 为闭集且
为闭集且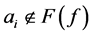 )。
)。
对上述 ,我们可以找到
,我们可以找到 满足引理5,且
满足引理5,且 (
( 表示
表示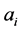 的
的 邻域),
邻域), 。下证上述
。下证上述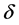 满足引理6。
满足引理6。
反证,若存在 循环
循环 ,设
,设 。
。
显然 ,我们不妨设
,我们不妨设 (根据
(根据 的性质以及
的性质以及 的选取,我们可以找到一个
的选取,我们可以找到一个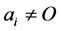 ,则令
,则令 ),
),
设 除
除 外的端点数为
外的端点数为 ,
,
A) 当 ,不妨设
,不妨设 除
除 外的端点为
外的端点为 ,则
,则
 且
且 ,
,
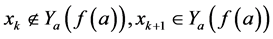 (1)
(1)
设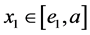 满足(1)式的最靠近
满足(1)式的最靠近 的点。
的点。
 (2)
(2)
设 的下标
的下标 为满足(2)式的最小下标,i.e.
为满足(2)式的最小下标,i.e.
 (3)
(3)
显然 。
。
下面分两种情况继续讨论:
(A1) 
在此情况下 ,且
,且 ,
, 从而
从而 且
且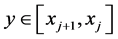 ,由引理4得
,由引理4得 ,与
,与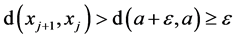 矛盾。
矛盾。
(A2)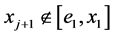 ,则有
,则有
由(A)中类似证明可得 。又
。又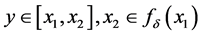 ,根据引理5,
,根据引理5, 与
与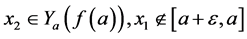 矛盾。
矛盾。
故我们选取的 满足引理6。
满足引理6。
(B) 当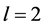 ,不妨设
,不妨设 除
除 外的端点为
外的端点为 。
。
(B1) 若仅有一个 满足(1)式的最靠近
满足(1)式的最靠近 的点,由(A)得引理6成立。
的点,由(A)得引理6成立。
(B2) 若存在两个不同点 满足(1)式的最靠近
满足(1)式的最靠近 的点。如(A)中,令
的点。如(A)中,令 的下标
的下标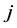 为满足(2)式的最小下标,
为满足(2)式的最小下标,
若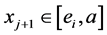 ,则令
,则令 。类似(A)中情况得引理6成立;
。类似(A)中情况得引理6成立;
若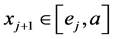 ,则令
,则令 。类似(A)中情况得引理6成立。□
。类似(A)中情况得引理6成立。□
定义1 设 定义数
定义数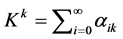 ,其中若
,其中若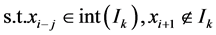 ,
, 且
且 ,则
,则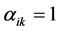 ;否则
;否则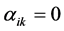 。(即
。(即 表示
表示 离开的次数)。记
离开的次数)。记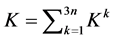 表示
表示 的区间指标。
的区间指标。
引理7 设 且
且 。考虑引理6中的划分
。考虑引理6中的划分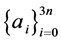 ,则
,则 ,
, ,使得任意
,使得任意 伪轨
伪轨 的区间指标小于
的区间指标小于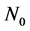 。
。
证明:根据引理6,我们选取的 足够小使得所有的
足够小使得所有的 循环伪轨在同一区间
循环伪轨在同一区间 内。
内。
假设引理7不成立,则存在一个 伪轨
伪轨 ,使得
,使得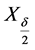 的区间指标
的区间指标 ,其中
,其中 为
为 的个数,
的个数, 。从而存在一个区间
。从而存在一个区间 ,使得
,使得 。
。
事实上取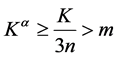 。
。
若存在某个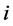 ,
, ,且
,且 ,则记
,则记 为
为 。
。
因为 ,所以我们可以找到超过m个类似
,所以我们可以找到超过m个类似 的点。于是
的点。于是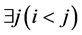 ,
, ,从而
,从而
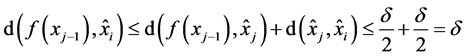 。
。
因此, 是一个
是一个 循环伪轨。由
循环伪轨。由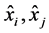 的定义知这个
的定义知这个 循环伪轨不全在区间
循环伪轨不全在区间 内,与假设矛盾。□
内,与假设矛盾。□
定义2 如果任意 ,我们有
,我们有 ,称不动点
,称不动点 的单边邻域
的单边邻域 为
为 的非吸收邻域。
的非吸收邻域。
引理8 设 且
且 。任取
。任取 ,其中
,其中 。设
。设 为
为 的非吸收邻域,若
的非吸收邻域,若 ,则我们有
,则我们有 。
。
证明:设 。因为
。因为 为
为 的非吸收邻域,则
的非吸收邻域,则 。由引理3得
。由引理3得 ,
,
(若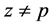 ,则
,则 。由
。由 ,
, ,
, )。
)。
又 ,
, ,所以
,所以 与引理3矛盾)故
与引理3矛盾)故 。□
。□
引理9 设 且
且 。设
。设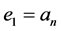 ,
,
 ,
,
 ,
,
 ,
,
如引理6中对 的划分,考虑
的划分,考虑 链
链 的某序列,其中
的某序列,其中 。设
。设 且
且 若
若 ,则
,则 。
。
设
 (4)
(4)
设 的极限存在,令
的极限存在,令 ,
,
若 ,则
,则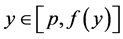 且
且 为
为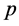 的非吸收邻域。
的非吸收邻域。
证明:若 ,则由
,则由 的连续性和(4)式得
的连续性和(4)式得 。
。
假设 ,显然有
,显然有 。因为
。因为 ,
, ,
,
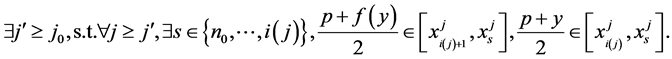 (5)
(5)
应用引理6中类似的方法,我们可以找到 。
。
因此有(5)式得,对 ,我们有
,我们有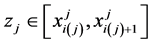 ,
,
其中
 (6)
(6)
与引理5矛盾。故 。
。
下证 为
为 的非吸收邻域。
的非吸收邻域。
假设 不是
不是 的非吸收邻域,则存在
的非吸收邻域,则存在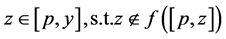 ,且
,且 。
。
若我们取 足够大(相应的
足够大(相应的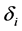 足够小),则
足够小),则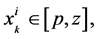 从而有
从而有 ,其中
,其中 (显然
(显然 )。因此若
)。因此若
( 存在),则
存在),则 。由
。由 的一致连续性,我们可以找到
的一致连续性,我们可以找到 ,从而
,从而 。
。
通过上述类似的方法,我们可以找到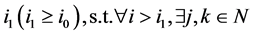 ,满足
,满足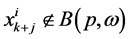 ,
,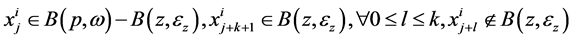 。根据上述(6)式类似得,与引理5矛盾。因此,
。根据上述(6)式类似得,与引理5矛盾。因此, 为
为 的非吸收邻域。显然有
的非吸收邻域。显然有 也为
也为 的非吸收邻域。□
的非吸收邻域。□
3. 主要定理的证明
定理 设 且
且 ,
,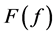 无处稠密。则下列条件等价:
无处稠密。则下列条件等价:
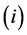 若
若 收敛与不动点
收敛与不动点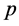 ,且
,且 的非吸收邻域
的非吸收邻域 ,则对于所有的
,则对于所有的 (
( 的邻域),
的邻域), 。
。

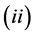 具有伪轨跟踪性。
具有伪轨跟踪性。
证明:
假设 不具有伪轨跟踪性,则
不具有伪轨跟踪性,则 链序列
链序列 不被
不被 跟踪,其中
跟踪,其中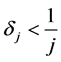 。
。
类似引理6对 的划分,并且
的划分,并且
 (7)
(7)
根据引理7,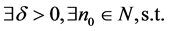 任意
任意 的区间指标
的区间指标
 (8)
(8)
不失一般性,假设 ,因此
,因此 ,其中
,其中 为
为 的区间指标。
的区间指标。
设
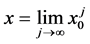 (9)
(9)
(必要时考虑相应的子序列),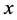 为
为 的起始点的极限点。由引理4和引理9,我们有
的起始点的极限点。由引理4和引理9,我们有
 且
且 (10)
(10)
因为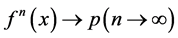 ,所以
,所以
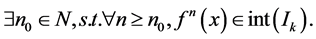 (11)
(11)
由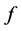 的连续性得,
的连续性得,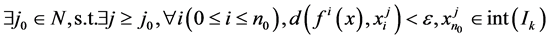 。
。
若 ,则显然
,则显然 被
被 的轨道
的轨道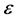 跟踪,与我们假设矛盾。因此
跟踪,与我们假设矛盾。因此
 (12)
(12)
现在我们考虑满足(12)式的最小值,不妨设为 ,故
,故
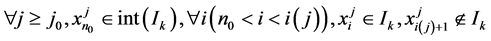
令
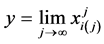 (13)
(13)
(如若必要我们考虑相应的子序列)
不失一般性设 ,由(9)-(13)式和引理9得
,由(9)-(13)式和引理9得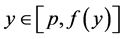 且
且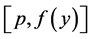 也为
也为 的非吸收邻域。由引理8,我们可以找到
的非吸收邻域。由引理8,我们可以找到 。
。
根据 的连续性,
的连续性,
 (14)
(14)
其中 ,
,
 (15)
(15)
根据我们的假设有 ,因此
,因此
 的邻域
的邻域
 (16)
(16)
因为 为
为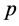 的非吸收邻域,所以
的非吸收邻域,所以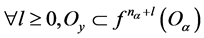 。
。
断言:

 ;
;

 。
。
证明断言:由 以及
以及 的连续性,
的连续性,
 (17)
(17)
(对于 的选取,我们可以简单的通过去掉
的选取,我们可以简单的通过去掉 得到)
得到)
设 为满足(17)式的最大区间,由归纳得我们可以找到
为满足(17)式的最大区间,由归纳得我们可以找到 ,
, 。
。
当 时,令
时,令 得
得
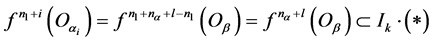 。□
。□
下证 式。若
式。若 ,则
,则 。
。
假设 ,则
,则
 ,
,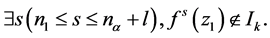 (18)
(18)
令 为满足(18)式的最小值。由引理3得,
为满足(18)式的最小值。由引理3得, (
( 为最小值)。又
为最小值)。又 为
为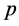 的非吸收邻域,则
的非吸收邻域,则 与
与 矛盾,故
矛盾,故 。□
。□
根据(7),(12),(14)以及断言,我们取 ,
,
对任意 ,存在区间
,存在区间
 且
且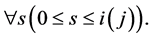 (19)
(19)
对于以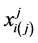 为始点的
为始点的 链序列
链序列 ,以及
,以及 ,则
,则 ,
, 链序列
链序列 不能被
不能被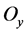 中的任一点的轨道
中的任一点的轨道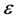 跟踪。(若
跟踪。(若 可被
可被 中的某一点
中的某一点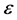 跟踪,则根据(19)式
跟踪,则根据(19)式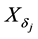 可被
可被 中的某一点的轨道
中的某一点的轨道 跟踪,与假设矛盾。)
跟踪,与假设矛盾。)
因此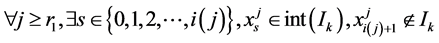 ,从而
,从而 。
。
重复上述过程, 邻域
邻域
 且
且 不能被
不能被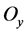 中的任一点的轨道
中的任一点的轨道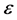 跟踪。故
跟踪。故 。
。
经过重复 次后,
次后, ,与(8)式矛盾。
,与(8)式矛盾。

设 为
为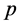 的非吸收邻域。
的非吸收邻域。 的某邻域
的某邻域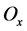 ,使得
,使得
 (20)
(20)
假设存在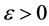 使得
使得
 且
且 (21)
(21)
由引理8,存在 使得
使得
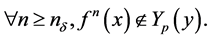 (22)
(22)
设 。令
。令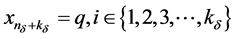 ,定义如下:
,定义如下:
若 ,则令
,则令 ;
;
若 ,则令
,则令 ,且
,且
 。(因为
。(因为 为
为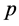 的非吸收邻域,所以上述定义是有意义的)
的非吸收邻域,所以上述定义是有意义的)
因此通过(23)式得 为
为 链。若
链。若 ,由(21)式有
,由(21)式有 ;若
;若 ,由(20)和(22)式有
,由(20)和(22)式有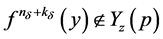 ,从而
,从而 。
。
故 链序列
链序列 不能被
不能被 跟踪,与假设矛盾。□
跟踪,与假设矛盾。□
推论 设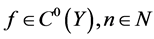 ,则
,则 具有伪轨跟踪性当且仅当
具有伪轨跟踪性当且仅当 具有伪轨跟踪性。
具有伪轨跟踪性。
证明:详细证明参考文献 [3] 引理9。
基金项目
国家自然基金(NO:11461002;11401288);广西自然科学基金(NO:2016GXNSFAA380317)。
文章引用
唐亚林,黄日娣,叶成博,张更容. Y 空间连续自映射的伪轨跟踪性
Shadowing Property of Continuous Maps in Y Space[J]. 应用数学进展, 2017, 06(01): 45-53. http://dx.doi.org/10.12677/AAM.2017.61006
参考文献 (References)
- 1. Gedeon, T. and Kuchta, M. (1992) Shadowing Property of Continuous Maps. American Mathematic Society, 115, 271-279. https://doi.org/10.1090/S0002-9939-1992-1086325-3
- 2. 赵俊玲. 动力系统中伪轨跟踪性的研究[D]: [博士学位论文]. 浙江大学, 2003.
- 3. 孙太祥. 树映射的 极限集与湍流[J]. 数学学报, 2002(45): 253-260.
- 4. 孙太祥, 席鸿建, 张更容, 陈占和.树映射的动力学[M]. 南宁: 广西科学技术出版社, 2011: 1-3, 16-17.
*通讯作者。