Advances in Applied Mathematics
Vol.
08
No.
05
(
2019
), Article ID:
30262
,
8
pages
10.12677/AAM.2019.85102
Kolmogorov
-Width of Infinite-Dimension Identity Operators in Probabilistic Frames
Jin Chen, Hanyue Xiao
School of Science, Xihua University, Chengdu Sichuan
Received: Apr. 25th, 2019; accepted: May 10th, 2019; published: May 17th, 2019

ABSTRACT
In this paper, we consider the Kolmogorov
-width of infinite-dimension identity operator
in probabilistic frames, and obtain its asymptotic degree.
Keywords:Identity Operator, Kolmogorov N-Width, Asymptotic Degree, Probabilistic Frames

概率框架下无穷维恒等算子的 Kolmogorov
-宽度
陈锦,肖寒月
西华大学理学院,四川 成都
收稿日期:2019年4月25日;录用日期:2019年5月10日;发布日期:2019年5月17日

摘 要
本文讨论了无穷维恒等算子
在概率框架下的宽度,并计算了其精确渐近阶。
关键词 :恒等算子,Kolmogorov n-宽度,渐近阶,概率框架

Copyright © 2019 by author(s) and Hans Publishers Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/


1. 引言及主要结果
宽度理论是函数逼近论的重要内容之一,也是国内外研究的热点之一,它与计算复杂性有着密切的联系 [1] 。宽度问题是Kolmogorov [2] 在1936年首次提出的一个概念,并给出了Sobolev函数类
到
上的Kolmogorov n-宽度的精确渐近阶。1954年,Stechkin [3] 研究了在
特殊情况下有限维空间的 Kolmogorov n-宽度的精确渐近阶与线性n-宽度的精确渐近阶。1960年,Tikhomirov [4] 给出了宽度
的精确渐近阶。此后两年,Pietsch [5] 和Stein [6] 研究了在一般情形下,
时Kolmogorov n-宽度的精确渐近阶与线性n-宽度的精确渐近阶。1974年,Ismagilov [7] 研究了当
时的精确渐近阶估计。1985年,Pinkus [8] 给出了有限维恒等算子的Kolmogorov n-宽度。王桐心 [9] 给出了无穷维恒等算子的在最坏框架下的Kolmogorov n-宽度。本文主要讨论无穷维恒等算子在概率框架下的Kolmogorov
-宽度。
首先,我们给出需要用到的基本定义和记号。
定义1.1 [8]:设W为赋范性线性空间
的一非空子集,
,称
为W在Y中的Kolmogorov n-宽度,其中
取遍Y中的维数不超过n的所有线性子空间。
定义1.2 [8]:设
为两个赋范线性空间,其范数分别为
与
,T是X到Y的有界线性算子。记
,
称
(1)
算子T的Kolmogorov n-宽度,其中
表示X的单位球,即
。
定义1.3 [10]:设B为W的全部开子集所生成的Borel域,在B上赋予概率测度
,即
为定义在B上的σ-可加的非负函数,且有
,令
,
则称
为W在
中的Kolmogorov概率
-宽度,其中
表示取遍B中所有测度不超过
的子集。
并称
(2)
为算子Kolmogorov
-宽度,其中
表示取遍B中所有测度不超过
的子集,
取遍Y中的维数不超过n的所有线性子空间。
设
,令
可知
为
上的一个范数,且
为Banach空间,且
当 时,
,而
。
时,
,而
。
故而可知:无穷维恒等算子是
的有界线性算子,而不是
到
的有界线性算子。
对于
,令
则可知,
为
上的范数,且
为Banach空间,记
为
中的单位球。
令
时,对
由Hȍlder不等式:
因此
,于是无穷维恒等算子 定义为:
定义为:
则
为
到
上的有界线性算子。
本文利用离散化的方法讨论了概率框架下无穷维恒等算子的Kolmogorov
-宽度,并得到其精确渐近阶。这就是本文的主要结果,即
定理1:设
,则
其中,符号“
”的定义如下:假设
是和参数
有关的非负常数。对两个正函数
和
,
,如果存在正常数
满足条件
,则记
。若存在正常数
满足条件
,则记
,若
且
,则记 。
。
2. 主要结果的证明
首先介绍有限维空间的Kolmogorov
-宽度的相关结论。
令
。
设
,
则
为
上的范数,
表示
按范数
所构成的Banach空间。
记
为
的单位球,则易知
为
的基,其中
引理1 [8] [10]:(1)设
,则
,则有
.
首先建立离散化定理:
定理2:设
,
,非负整数序列
满足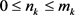 ,且
。则
,且
。则
.
为了证明定理2,我们先介绍一些记号:对
,其中
,记
,则
,且
,有
,用
表示
中元素的个数,则
。
,有
这里
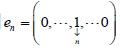 ,且
为
的Schauder基。
,且
为
的Schauder基。
对于
,记
,则
。
令
则 ,有
,有
(1)
且
(2)
从而
为
到
上的等距同构映射。
据Gaussian测度
的定义,在
中赋予标准Guassiam测度
对
,记
,
为所对应特征向量,
。
则可知:
记
于是
。
下面我们来估计定理2的上界:
即:设
,n为自然数,则
,对任意满足条件
的数列
,这里
,有
证明:
,
,有
由(2)式有
对于
,由Kolmogorov-
宽度的定义,可知存在
上的一个秩不大于
的恒等算子
,使得
对于
,有
令
由Gaussian测度
和标准Gaussian测度
的定义可得
令
,则
从而有:
现在,我们再来估计定理2的下界:
即:设
,则有
其中
。
证明:
,对
,则有
由
为
到
上的恒等算子,有
其中
。
设
,则有
所以
即:
综上可知,定理2得证。
有了离散化定理2,下面我们来证明本文的主定理即定理1。
证明:首先建立数列:
,
其中
且
,则
下面我们来证明定理1的上界:
即得到定理的上界
下面再来证明主定理1的下界:
设
,则
,且
于是
于是得到
.
综上可知,定理1得证。
文章引用
陈 锦,肖寒月. 概率框架下无穷维恒等算子的Kolmogorov (n,δ)-宽度
Kolmogorov -Width of Infinite-Dimension Identity Operators in Probabilistic Frames[J]. 应用数学进展, 2019, 08(05): 902-909. https://doi.org/10.12677/AAM.2019.85102
参考文献
- 1. Traub, J.F., Wasilkowski, G.W. and Wozniakowski, H. (1988) Information-Based Complexity. Academic Press, Bos-ton.
- 2. Kolmogorov, A.N. (1936) Uber die deste Annaherung yon funktionen einer gegebenen funktioneklasse. An-nals of Mathematics, No. 37, 107-111. https://doi.org/10.2307/1968691
- 3. Stechkin, S.R. (1954) On Best Ap-proximation of Given Classes of Functions by Arbitrary Polynomials. Uspekhi Matematicheskikh Nauk, 9, 133-134. (Russian)
- 4. Tikhomirov, V.M. (1960) Diameters of Sets in Function Spaces and the Theory of Best Approximations. Uspekhi Matematicheskikh Nauk, 15, 81-120. (English Translation in Russian Mathematical Surveys, 15, 75-111.)
https://doi.org/10.1070/RM1960v015n03ABEH004093
- 5. Pietsch, A. (1974) S-Numbers of Operators in Ba-nach Spaces. Studia Mathematica, No. 51, 201-223.
https://doi.org/10.4064/sm-51-3-201-223
- 6. Stesin, M.I. (1975) Aleksandrov Widths of Finite-Dimensional Sets and Classes of Smooth Functions. Doklady Akademii Nauk SSSR, 220, 1278-1281. (English Translation in Soviet Mathematics, Doklady)
- 7. Ismagilov, R.S. (1974) Widths of Sets in Normed Linear Spaces and Approximation of Functions by Trigonometric Polynomials. Uspekhi Matematicheskikh Nauk, 29, 161-178. (English Translation in Russian Mathematical Surveys, 29, 169-186.) https://doi.org/10.1070/RM1974v029n03ABEH001287
- 8. Pinkus, A. (1985) N-Widths in Approximation Theory. Springer, Berlin. https://doi.org/10.1007/978-3-642-69894-1
- 9. 王桐心. 无穷维恒等算子的Kolmogorov n-宽度[J]. 应用数学进展, 2018, 7(5): 519-524.
- 10. Maiorov, V.E. (1994) Kolmogorov’s -Widths of the Spaces of the Smooth Functions. Russian Academy of Sciences. Sbornik Mathe-matics, 79, 265-279. https://doi.org/10.1070/SM1994v079n02ABEH003499


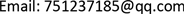




 时,
,而
。
时,
,而
。 定义为:
定义为: 。
。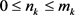 ,且
。则
,且
。则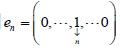 ,且
为
的Schauder基。
,且
为
的Schauder基。 ,有
,有