International Journal of Mechanics Research
Vol.06 No.02(2017), Article ID:21130,17
pages
10.12677/IJM.2017.62013
Research on Characteristics of All State Function of Elastic-Plastic Materials
Zhenhai Wei1, Mengshu Wang2, Dingli Zhang2
1School of Rear Professional Service, Logistics Command Academy, Beijing
2School of Civil Engineering, Beijing Jiaotong University, Beijing

Received: Jun. 6th, 2017; accepted: Jun. 24th, 2017; published: Jun. 27th, 2017

ABSTRACT
Elastic-plastic materials are a typical material researched in classic elastic-plastic theory, and it’s of great theoretical significance to verify the accuracy and applicability of theoretical method based on the research on elastic-perfectly plastic materials with the theories of structural all state function. With the theoretical method of structural all state function, the paper obtains control partial differential equations, path equation and constitutive relation as well as three analytical solutions under special states, namely plane-form solution, cylindrical-form solution and spherical-form solution, of all state function of elastic-perfectly plastic materials. According to the research, it’s discovered that the all state function of elastic-perfectly plastic materials is consistent with strength theory of classic elastic-plastic theory in form completely, and moreover, the path equation obtained is consistent with the flow rule completely and the constitutive relation conforms to the form in classic elastic-plastic theory completely as well. So far, it’s proved that it’s able to obtain conclusions and results completely same with classic elastic-plastic theory by means of applying the theories of structural all state function to elastic-perfectly plastic materials. More importantly, the concepts, theories and methods of all state function unify the strength theory, flow rule and constitutive relation in classic elastic-plastic theory under a theoretical framework and endow them unified theoretical basis.
Keywords:Structure Materials, All State Function, Path Equation, Flow Rule, Constitutive Relation
弹塑性材料全状态函数特征研究
卫振海1,王梦恕2,张顶立2
1后勤学院后方专业勤务系,北京
2北京交通大学土木建筑工程学院,北京
收稿日期:2017年6月6日;录用日期:2017年6月24日;发布日期:2017年6月27日

摘 要
弹塑性材料是经典弹塑性理论所研究的一种典型材料,应用材料结构全状态函数理论研究这一对象,对于验证理论方法的正确性和适用性具有重要理论意义。采用材料结构全状态函数的理论方法,获得了理想弹塑性材料全状态函数的控制偏微分方程组、状态路径方程和本构关系,以及三组特定状态下的解析解:平面形式、圆柱和球面形式的解。发现理想弹塑性材料全状态函数在形式上与经典弹塑性理论的强度理论形式完全一致,所得到的路径方程与流动法则相似,本构关系也与经典弹塑性理论形式相同。至此,证明了材料结构全状态函数理论应用于理想弹塑性材料,可得到与经典弹塑性理论完全相同的结论和结果。更重要的是材料结构全状态函数的概念、理论及方法,将经典弹塑性理论中的强度理论、流动法则和本构关系完全统一在一个理论框架之下,使其具有了统一的理论基础。
关键词 :结构性材料,全状态函数,路径方程,流动法则,本构关系

Copyright © 2017 by authors and Hans Publishers Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/


1. 引言
材料的强度理论、流动法则和本构关系是经典弹塑性理论的基础和核心内容,但这些概念长期以来是相互分离的,这使经典的弹塑性理论体系缺少了统一的理论基础。许多学者都在这方面做过认真、仔细和大量的研究,也取得了不少的成果。强度准则是以Tresca和Misses理论为基础,虽然许多学者也提出了不少新的准则 [1] - [11] ,但理论的基础和基本的概念并没有大的变化。流动法则以塑性势概念为基础,不少学者在这方面也提出了新的思想 [12] - [22] ,但突破性成果罕有见到。至于本构关系的探讨和研究,成果更是不计其数 [13] [23] - [32] ,但大都没有脱离应力-应变关系的传统概念。强度理论、流动法则和本构关系在概念体系上基本是分离的,缺少相应的统一的理论基础。从已有的成果可以看到,对材料力学性能研究工作的基础和实质,仍然是弹性理论的概念体系。在研究塑性材料时,还是在弹性理论的基础上,引入局部的与材料塑性有关的新假定或定义,对弹性理论加以补充,以适应塑性材料的表观现象与特征。材料结构全状态函数理论以一种新观点来看待塑性问题 [31] [32] [33] [34] 。认为塑性是材料几何形态变化的一种外在表现,其实质是材料结构的变化。通过采用材料结构变化的概念,来分析影响材料结构变化的特征量的关系,建立起描述材料结构状态的全状态函数,作为分析材料性能特征的基础。
理想弹塑性材料,可以认为是结构性材料的一个特例,即材料的结构趋于均匀结构。本文试图用材料的结构全状态函数理论和方法,来分析这一特殊性的结构材料。作为一种比经典弹塑性理论更具普遍性的理论,材料结构全状态函数理论应能很好地解决和分析均匀结构的理想弹塑性材料这一特例。分析的结果也很好地证明了这一点。
2. 材料结构全状态函数模型及基本假定
2.1. 材料结构全状态函数理论 [31] [32] [33] [34] 的分析思路
材料的结构性是材料的一种普遍特性。结构性的强弱与材料特点,特别是我们观察材料的尺度直接相关。金属类材料由于其均匀性较强,结构性相对表现的不明显,但岩土类材料结构性就非常强。材料在宏观上表现出来的变形特征可以分为弹性变形和塑性变形。从材料结构的角度来看,弹性变形可以认为是材料结构在保持原有形态情况下的结构的弹性变形,塑性变形可以认为是材料的结构发生了变化,也就是结构的形态从一种形态变化到另一种形态的变化。由此看到,弹性变形与塑性变形有着本质的区别。
一般性的材料,在一定尺度上观察其构成的结构情况,是相当复杂的。结构的各种参数也是不一致,也就是不均匀的。可以认为材料特定结构形态下的强度、结构弹性模量和结构的形态变化的几何量是描述材料结构的三个(类)基本参数。这三个(类)参数从三个不同的侧面描述了材料的结构状态。如果将材料的所有这种结构状态的描述,放在由应力-刚度-应变构成的相空间中,每一种状态是相空间中的一个点。将材料结构的所有可能的状态在相空间中都描述出来,根据材料结构全状态函数理论的假定,从宏观上就构成了相空间中的材料结构的全状态函数(超曲面)。这一全状态函数实质上是材料所有可能结构状态的集合,是材料结构特性的综合反映。全状态函数曲面的特征代表了材料的特性,所以也可以认为材料结构全状态函数是材料特性在各种不同结构状态下的表现。
基于材料结构全状态函数,可以分析材料在受到各种环境(荷载)影响时,材料结构可能的变化状态。由于材料结构全状态函数包含了材料结构所有的可能变化状态,所以,任何特定的荷载作用的影响,只能限于沿全状态函数曲面上进行变化。当给定了某一荷载作用时,材料结构为适应外部的影响,材料结构将发生变化,这就构成材料结构状态变化的特定路径,而这一路径反映了材料的局部特性。状态路径曲线的切线,实质上就反映了材料在这一变化路径上的,局部的应力-应变关系,也就是材料的本构关系。但这里的本构关系是塑性本构关系。所以,求得材料结构全状态函数,是解决具有结构特性材料的关键和核心内容。
2.2. 基本假定
对于一般的结构性材料,问题比较复杂,为了简化问题,将材料的结构认为是均匀的,可以认为是一种理想结构状态,这样就很接近于经典理论中的理想弹塑性材料。要导出均匀结构的理想弹塑性材料的全状态函数,主要基于如下假定:
(1) 材料的结构均匀分布,且可近似认为连续和各向同性;
(2) 材料结构的极限弹性能密度在应力-刚度-应变空间中的确定区域中是常量或有限量,并可描述;
(3) 在应力-刚度-应变空间中,材料结构状态的强度-弹性模量-结构几何应变构成材料结构状态参数,所有可能的结构状态构成结构状态函数,可称为全状态函数;
(4) 理想弹塑性材料的结构全状态函数与结构的几何应变分量无关,且材料的结构刚度(弹性模量)为常量;
(5) 材料结构变化过程中具有保持其原有状态的趋势和特征,也可称之为状态贯性特性。在结构必须变化时,有尽量保持少的变化的趋势;
(6) 材料结构的强度-结构应变路径满足最小能量原理。
结构性材料在受到力作用后,各向同性的特性会受到破坏,第一条假定是为了简化这一复杂的特性。第二条假定是认为,材料结构状态在一定的变化区域内,材料结构在最大强度下,结构的弹性能总量对于特定的材料是一个常量。第三条假定,认为存在一个函数面,这个函数面反映了材料结构所有可能的结构状态。第四条假定是为了简化分析,只考虑材料结构强度的影响和变化,而使问题得到大大的简化。在一般性问题中,由于材料的结构形态在不断变化,结构的弹性模量并不是常量,但对于宏观上完全均匀的材料,从统计角度来讲,其结构的弹性模量是常量是符合实际情况的。第五条假定认为材料的结构受到外界作用时,总是努力保持原有状态不变,当不能不变时,以尽量少的变化来适应外部的作用。这一条在本质上与第二条有相通之处。第六条认为受到外部作用时,沿全状态函数曲面的变化,总是选择能量消耗最小的路径变化。
2.3. 材料理想结构状态全状态函数模型及方程
根据第(5)条假定,材料结构在变化的过程中,总是尽可能地保持材料结构的弹性状态,在环境(荷载)作用下,材料结构发生变化时,可以认为结构性材料总是尽可能地保持其原有状态,这样,可以认为材料结构的全状态函数面,是材料维持其弹性结构的极限面。在全状态函数面内部,材料维持其弹性状态。在全状态函数面外部,材料结构发生破坏。在全状态函数面上,材料结构发生变化,从一种结构状态过渡到另一种结构状态。
根据第四条假定,由于与应变和刚度无关,用主应力来表示全状态函数。全状态函数则是主应力空间中的一个曲面。因此,参数形式的材料结构全状态函数的形式可表达为:
 (1)
(1)
其中, 、
、 、
、 为三个主应力,u、v为曲面参数。
为三个主应力,u、v为曲面参数。
这一曲面包裹着材料的结构。函数曲面面积的大小随函数曲面的具体形态而变化,并考虑材料结构弹性能的约束时,因此存在泛函:
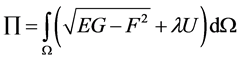 (2)
(2)
这里,
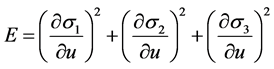
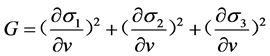
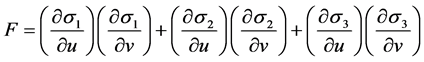
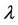 为待定参数。
为待定参数。 ,
, 为材料结构的极限弹性能密度函数。
为材料结构的极限弹性能密度函数。
实际的材料结构全状态函数曲面,是这一泛函的极值面。这里设: ,由变分原理可知,满足式(2)的极值面的方程必然满足欧拉方程:
,由变分原理可知,满足式(2)的极值面的方程必然满足欧拉方程:
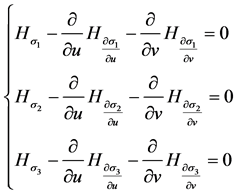
其中:
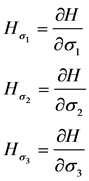 ,
,  ,
, 
将H的表达式具体内容代入,整理后得欧拉方程:
 (3)
(3)
这就是参数形式的材料结构全状态函数的控制偏微分方程组。再加上合适的边界条件,就可以确定具体的全状态函数的曲面方程形式。但由于这一方程组是一非线性方程组,求解其解析解是比较困难的,只能求得一些特殊条件下的解析解。对于某些问题可以采用数值解法,这对于了解和掌握材料结构全状态函数的性质是十分有意义的,为掌握结构性材料的性质有了一种新的方法。
2.4. 状态路径方程
根据材料结构全状态函数的假定,材料结构全状态函数反映的是材料性能的集合,对于在某环境因素(荷载)作用下的状态具体变化,是在满足确定的约束条件下,沿全状态函数面局部的变化。其中内在的约束条件,是材料状态总是以能量最小的方式进行变化。
对于理想状态的结构性材料,材料结构全状态函数中,D为常量,且与结构应变无关,因此可设全状态函数的形式为:
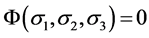 (4)
(4)
考虑能量最小原理和拉格朗日方法,存在泛函:
 (5)
(5)
这里 为待定常数。如果设路径方程可以表达为参数形式,则有:
为待定常数。如果设路径方程可以表达为参数形式,则有:
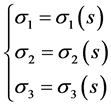 和
和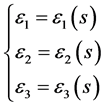 (6)
(6)
这里s为路径方程参数。则有:

 (7)
(7)
设: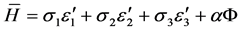 ,求其变分方程,得,欧拉方程:
,求其变分方程,得,欧拉方程:


代入 的具体内容,整体后有欧拉方程:
的具体内容,整体后有欧拉方程:
 (8)
(8)
显然这里有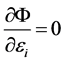 ,所以有
,所以有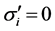 。也就是说应力强度的增量为零。这样就得到:
。也就是说应力强度的增量为零。这样就得到:
 (9)
(9)
这实际是应变路径上的导数与全状态函数的关系。注意这里的应变实际是材料的结构状态变化时的应变,也就是宏观上的塑性应变。
2.5. 本构关系
对于路径方程(6),可以得到切线方程: 。如果设
。如果设 ,就得到:
,就得到:

将式(9)代入,得:
 (10)
(10)
令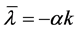 ,结构应变实质就是宏观上的塑性应变,也可以认为是经典理论中塑性应变,即
,结构应变实质就是宏观上的塑性应变,也可以认为是经典理论中塑性应变,即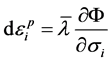 。这样就得到和经典弹塑性理论的流动法则完全一致的表达形式。
。这样就得到和经典弹塑性理论的流动法则完全一致的表达形式。
另外,考虑全状态函数的切面方程,有:
 (11)
(11)
考虑材料的全应变为弹性应变和塑性应变之和,即:

这里 为材料的全应变;
为材料的全应变;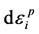 为材料的塑性应变,也就是材料的结构应变;
为材料的塑性应变,也就是材料的结构应变; 为材料的弹性应变。所以,有:
为材料的弹性应变。所以,有:
 (12)
(12)
将式(12)代入式(11)中,解得:
 (13)
(13)
再将式(13)代入式(12)中,得:
 (14)
(14)
这就是理想弹塑性材料的本构关系,其中Dij为材料的弹性模量。
材料全状态函数、状态路径方程和本构关系这三部分构成问题的完整的解决方法和过程。
3. 特定问题的解
材料结构全状态函数的控制偏微分方程组(3),是一组非线性偏微分方程,一般情况下,求得其解析解是十分困难的。特别是在给定某种边界条件下,更是如此。根据前面的讨论可知,只有在求出全状态函数的具体形式,才能求解状态路径方程和本构关系的具体形式。所以,求得全状态函数的具体表达形式,是解决问题的关键。
下面针对三种特殊情况,求解该问题。
3.1. 平面形式的解答
设结构极限弹性能密度函数的形式为:
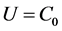 (15)
(15)
这里C0为常量,即结构极限弹性能密度函数为常量。另设解的形式为:
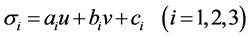 (16)
(16)
则有:
 (17)
(17)
 (18)
(18)
将式(15)、(17)和式(18)代入方程(3)中,方程(3)将自动满足。但这里存在ai、bi、ci共9个待定常数,这9个待定常数需要边界条件来确定。
下面针对一些简单边界条件进行讨论。
设 。这样方程的解为:
。这样方程的解为:
 (19)
(19)
由此,就得到:
 (20)
(20)
可以证明,任意两个平面的交线的方向与等倾轴的方向一致,也就是说,这个方程组围成的图形是一个与等倾轴平行的梭柱体。当 时,并考虑对称性时,可得到经典理论中的Tresica强度理论。
时,并考虑对称性时,可得到经典理论中的Tresica强度理论。
设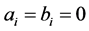 ,这样方程的解为:
,这样方程的解为:
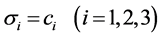 (21)
(21)
并考虑对称性,就得到一个将原点围于中心的矩形,这实质上是经典理论中的最大拉应力准则(Rankine准则)。当ci取不同的值时,图形围成的区域不同,可得到不同形式的强度准则。
由此看到,不同的边界条件,可以得到不同的全状态函数图形,在这里也可以认为是不同的强度准则。
3.2. 圆柱面形式的解答
设材料结构极限弹性能密度函数为:
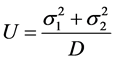 (22)
(22)
这里D为材料弹性模量。
设解的形式为:
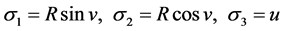 (23)
(23)
这样有:
 (24)
(24)
代入方程(3)中,有:
 (25)
(25)
如果 ,则方程两边相等,所设定的解满足方程(3)。实际上,所有圆心通过原点的柱面方程,都可以满足偏微分方程(3),只是材料结构极限弹性能密度函数的形式要作相应的变化。下面推导与经典理论中的Misses准则相同形式的全状态函数。
,则方程两边相等,所设定的解满足方程(3)。实际上,所有圆心通过原点的柱面方程,都可以满足偏微分方程(3),只是材料结构极限弹性能密度函数的形式要作相应的变化。下面推导与经典理论中的Misses准则相同形式的全状态函数。
设全状态函数的形式为:
 (26)
(26)
设强度能量密度函数为:
 (27)
(27)
由此得:
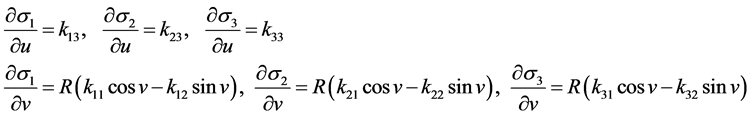 (28)
(28)
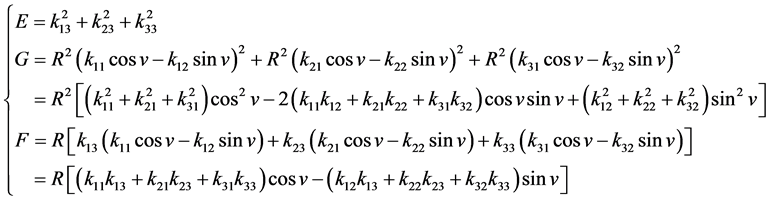 (29)
(29)
如果设矩阵[K]的三个列向量为单位向量,且相互垂直,则有:
 (30)
(30)
这样就有:
 (31)
(31)
同时有:

将式(28)和式(31)代入方程(3),并比较方程两边,得:
 (33)
(33)
方程(30)和方程(33)联合求解:
由方程组(33)的最后一组,可解出 ,代入方程(30)中得到
,代入方程(30)中得到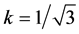 。令
。令 ,方程(33)化为:
,方程(33)化为:
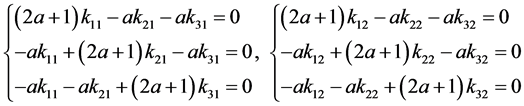 (34)
(34)
该方程组有非零解的条件为:
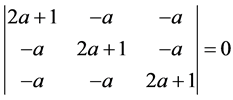 (35)
(35)
解得 ,则得
,则得 。
。
通过化简,从方程(33)可以得到:
 (36)
(36)
与方程(30)联立求解:

得: ,代入:
,代入:
 (37)
(37)
得:
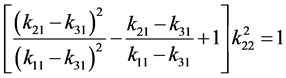 (38)
(38)
同理有:
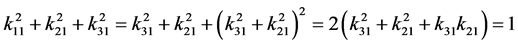 (39)
(39)
如果将k31看作已知量,则有:
 (40)
(40)
显然,必须有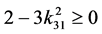 ,即
,即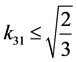 ,为方便取
,为方便取 ,则可得:
,则可得:
 (41)
(41)
实际上这是一个旋转矩阵,就是经过坐标轴的旋转,将轴心与 轴重合的圆柱曲面转换到了等倾轴上,也就是圆柱面的轴与等倾轴重合。
轴重合的圆柱曲面转换到了等倾轴上,也就是圆柱面的轴与等倾轴重合。
可以证明,任意方向的圆柱面的轴只要通过原点,其结构极限弹性能密度函数,只要在与圆柱轴垂直的平面上的投影为圆,则该曲面都是方程(3)的解。这告诉我们,理想弹塑性材料的全状态函数是一个圆柱面,且这个圆柱面的方向,可随复杂应力条件下的材料特性而变化。
状态路径方程:
对于理想弹塑性材料其路径方程为:

由于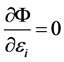 ,所以有
,所以有 ,则有:
,则有:
 (42)
(42)
将式(26)整理,将消去参数后,由路径方式中的第一式并结合式(42),可得:
 (43)
(43)
这里的B1、B2、B3这常量。
由此可以看到,强度和结构应变均为线性变化。
这里的全状态函数是一个圆柱面轴与等倾轴重合的柱面,和经典理论中Misses理论具有完全相同的形式。
3.3. 圆球曲面形式的解
设解的形式为(这实际上一个球面):
 (44)
(44)
材料结构极限弹性能密度函数为:

相应有:


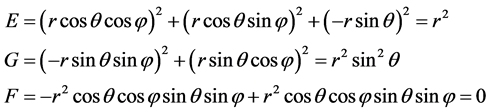
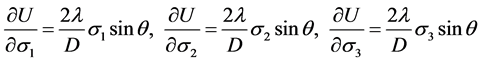
将以上各式代入方程(3),得:
 (45)
(45)
整理后,发现如 ,则方程两端自动满足。所以,所假定的解是方程的一个解。
,则方程两端自动满足。所以,所假定的解是方程的一个解。
由此看到,由于方程(3)是一个非线性的偏微分方程组,求得其解析形式的解是比较困难的。但在一些特殊条件下,可以求得一些特定解。这些特定的解也能反映出材料结构全状态函数的某些特征,特别是理想状态的结构性材料的全状态函数特征,可以从前面的平面形式的解、圆柱面和球面形式的解反映出来。另外,解的边界条件是影响解的形态的另一个重要因素。还有一个反映材料特征,并影响解的特征的重要因素就是材料结构极限弹性能密度函数。材料结构极限弹性能密度函数反映了材料的重要特性,和材料的微观或细观上的结构、联接形态和连接性能有着密切关系。
4. 几点讨论
通过前面的分析,得到了材料结构在理想弹塑性状态下的全状态函数的控制方程,并依据全状态函数求得了状态路径方程和本构关系。通过对控制方程的分析,求得了某些特殊形式的解析解,如平面形式、圆柱面形式和球面形式的解。由此加深了对材料结构全状态函数理论的认识。主要可以表现在以下几个方面。
4.1. 理想材料全状态函数的特征
理想弹塑性材料的全状态函数,具有一些独特的特征,这些特征主要可以表现在以下几个方面:
(1) 曲面特征
可以发现对于理想弹塑性材料,根据控制方程组(3)求得的平面解、圆柱面解和球形解,都具有凸曲面特征。分析控制方程组(3)和形成控制方程组的泛函方程(2),以及其物理本质,可以发现材料结构的变化,应遵守一条原理:也就是状态变化的惯性原理。材料结构在受到外部环境作用时,总是在努力地保持其原有的状态,在不能保持其原有状态的情况下,将以最小的变化来适应外部环境的影响。对于理想弹塑性材料,结构的变化主要发生在全状态函数面上,全状态函数面的内部为材料的弹性结构状态。在外力的作用下,材料将尽可能大的保持这个弹性结构,而使全状态函数面达到最小,也就是尽可能小地发生变化。也可以理解为,在全状态函数面一定的情况下,使材料的弹性内核尽可能地大。由此可知,全状态函数面在一定的条件下为凸曲面函数。这与经典弹塑性理论中,假定材料的强度曲面为凸曲面的思想是一致的。
(2) 应力坐标旋转、平移的影响
根据控制方程(3),得到的平面形式、柱面和球面形式的解,在应力坐标旋转、平移的变换下,其状态曲面的形态并不发生改变,将仍然保持其平面、柱面和球面形态。对于控制方程组(3)中,发生变化的主要是材料结构极限弹性能密度函数U的形式。在不同的变换下,U的形式将发生变化。通过分析可以发现,只要保持U函数在变化中其形态不发生改变,其解的形态将也不发生变化,只要将原解的形式,
转换到新方向上即可。如圆柱面形式的解,圆柱的轴心平行于 轴时,
轴时,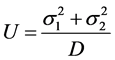 函数是一平行于
函数是一平行于 平面的圆,当将圆柱面轴转到与等倾轴重合时,在等倾面上
平面的圆,当将圆柱面轴转到与等倾轴重合时,在等倾面上 函数应该还是一个圆。如果坐标进行平移变换,则
函数应该还是一个圆。如果坐标进行平移变换,则 变换为
变换为 ,新的平移后的
,新的平移后的
圆柱面仍然是方程(3)的解。这揭示出一个信息:方程组(3)中的材料结构极限弹性能密度函数,其实质不是由材料的绝对强度值所决定,而是强度能量密度的变化值或相对值。这一特点使我们联想到材料的刚度位移,并不产生应变的道理。也就是说,应力强度值的变化,如果是统一增加,均匀变化,将不引起强度能量密度函数的形态变化,对方程的解也将不发生影响。所以,材料结构极限弹性能密度函数其实质是弹性能密度的变化率函数。另外也告诉我们,材料的结构特征不变,特别是理想弹塑性材料,材料结构极限弹性能密度函数在形态上不应变化。如前面讨论到的常数特征和圆柱特征,这种形态特征,在坐标的平移和旋转中是不变的。对于具有相同形态特征的材料结构极限弹性能密度函数的材料,可以通过各种不同的坐标变换,适用不同的强度边界条件,从而得到不同表达形式的全状态函数解。也可以说,这就是我们可以构造出无数材料的强度准则的原因。
(3) 对称轴和对称点特征
由于理想结构性材料具有各向同性,强度为常量的特点,对全状态函数必然存在一个对称轴或对称点。在复杂应力状态下,全状态函数的曲面可能有两种形态:一种是开口形态,如棱柱面或圆柱面;另一种是封闭形态。对于开口形态,要保持其“强度”不变,只能是剪应力强度。这样就形成不同形态的柱面形态,而由于材料的各向同性,柱面形态必然是对称的,必然存在一个对称轴,只能是对称形式的柱面。对于封闭的全状态函数,由于各向同性会存在一个对称原点,对于平面形式的解,在应力空间中就是立方体形态,曲面形式的解可以是圆球面形态。
4.2. 影响全状态函数特征的因素
从前面的分析可知,影响全状态函数特征的因素主要有三个:一是控制偏微分方程组(3);二是材料结构极限弹性能密度函数;三是边界条件。
(1) 控制偏微分方程组
控制偏微分方程组(3)是一组非线性偏微分方程。这类方程一般情况下,很难求得其解析形式的解。只有在一些特殊情况下,可以得到一些特定的结果。从方程组(3)中可以看到,方程的左边只与函数的一级导数有关,而与具体的坐标无关。在方程的右边,是材料结构极限弹性能密度函数的偏微分。不同形态的材料结构极限弹性能密度函数,使方程组的解必然有着不同的形态。对于不同的结构性材料,材料结构极限弹性能密度函数会有所不同,其解自然也会有所不同。就是理想状态的结构性材料,对于更复杂的材料结构极限弹性能密度函数,只能通过其他方法,求得其近似解析形式的解或数值解。
(2) 材料结构极限弹性能密度函数
根据前面的讨论可知,材料结构极限弹性能密度函数和相对的能量密度变化有关。对于不同结构性材料,能量密度函数也不同。能量密度函数的形态,反映了结构性材料的重要特征。对于理想弹塑性材料,目前所掌握的主要有两种形态:一种是可导致全状态函数在形态上为开口的能量密度函数;另一种是全状态函数的解的形态为封闭形式的解。可以这样认识这一特征:开口形态的解,反映的是材料的剪切强度特性,与静水压力无关。而封闭形态解的材料结构极限弹性能密度函数,却反映是与静水压力有关的材料的性质(如Rankine准则)。材料结构极限弹性能密度函数的形态特征,往往与全状态函数的特征密切相关。当然边界条件也是影响全状态函数特征的重要因素。
材料结构极限弹性能密度函数影响到全状态函数的特征,其实质是材料特性的反映。而材料的特性又和材料的结构特征密切相关。所以,要掌握材料结构极限弹性能密度函数的形态特征,就需要研究材料的结构特性,特别是材料结构演化过程中的能量密度的变化规律。
(3) 边界条件
影响全状态函数特征的另一重要因素是边界条件。控制偏微分方程组(3)解决的是曲面族的问题,而对于特定的材料,其全状态函数是一特定的曲面,这就要靠边界条件来确定。在多变量,即强度-刚度-结构应变空间中,强度条件可以作为一般性的全状态函数的边界条件,即

而对理想弹塑性材料,其边界条件可以进一步简化,因为这时的全状态函数在形式上是与强度准则一致的。只要给定某些局部的条件,就可确定相应的函数的具体形式。但由于控制偏微分方程组(3)是一组非线性偏微分方程组,求解曲面族的解析表达式是相当困难的,只有在某些特定的条件,才可能得到封闭解的结果。对于这些特殊形式的解,可以通过若干个点来作为其边界条件,来确定其解的具体形式。如平面形式的解,可以通过每个平面三个点的方式来确定,再利用对称原理,就可以将整个的全状态函数面确定下来。对于曲面形式的柱面或球面解,需要的条件更为复杂一些。但无论那种形式的解,边界条件都不会过于复杂,特别是通过实验来确定时,可大大减少实验的数据。
当然边界条件的确定,可以通过理论分析,也可以通过实验来获得。
4.3. 全状态函数理论的意义
本文依据材料结构全状态函数理论的思路与方法,分析了经典弹塑性理论中的典型材料:理想弹塑性材料问题。得到了一些特定情况下特殊解,由此证明了这一理论的作用和意义。使我们大大加深了对这一理论的认识,这主要表现在以下几个方面:
(1) 为解决结构性材料问题提出一套新的概念、理论和方法
经典弹塑性力学理论由于是建立在均匀、连续、无限可分的材料假定之上,这是继承了弹性力学的概念。经典理论忽略或简化掉了材料的一个重要特性:结构性。但如果考虑结构性,就完全破坏了弹塑性力学的基础。由于两者的矛盾,经典弹塑性力学理论不可能简单地解决结构性材料的问题。经典弹塑性材料由于其均匀性可以称其为简单材料,具有结构性材料可以称为复杂材料。简单材料与复杂材料的力学基础是矛盾的,但也存在着关联性,这就是复杂材料的极限状态就是简单材料。也可以认为简单材料是复杂材料的一个特例。过去长期以来,我们一直试图以简单材料的理论与方法去解决复杂材料的问题,这相当于用特殊理论与方法去解决一般性问题,这显然是行不通的。
材料结构的强度、弹性模量和几何形态的变化规律,就构成了材料结构在应力-刚度-应变空间中的材料结构全状态函数。材料结构全状态函数全面和整体地反映了材料的力学性能。材料结构全状态函数的实质是在所有可能的状态中,材料弹性结构状态和结构破坏的交界面函数。在这一界面的内部,材料保持了结构的弹性状态。在界面之外,材料的结构破坏,并不复存在。在界面之上,材料的结构发生演化,从一种状态演化到另一种状态。全状态函数曲面,从目前掌握的知识,推断是一个一定条件下的紧曲面。在掌握了全状态函数的特征后,就可以容易地解决状态路径问题和本构关系问题。
本文用材料结构全状态函数理论,分析经典理论中的弹塑性材料的意义在于证明全状态函数理论的概念与方法,在解决最简单,也就是理想结构状态的材料时,其结论与经典弹塑性理论是一致的和正确的。也就证明了作为一种一般性的理论和方法,可以解决弹塑材料这种特殊问题。从而从某一方面证明了材料结构全状态函数理论的正确性。
(2) 强度、流动法则和本构关系有了统一的理论基础
材料结构全状态函数全面和整体地反映材料性能,对于经典弹塑性理论中的强度理论、流动法则和本构关系也应该能够反映。通过对理想弹塑性材料的分析,完全证实了这一点。材料结构全状态函数是一个应力-刚度-应变空间构成的多维空间的函数。当我们单独考察应力子空间中的全状态函数特征时,全状态函数反映的是材料在复杂应力状态下的强度变化规律。当材料受特定的环境作用时,变化的过程就是结构状态的变化过程。因此,变化是沿全状态函数曲面上进行的一条路径。这条路径的变化,实际上反映的是在特定环境作用下,材料强度和材料的几何状态变化之间的关系。这一点类似于经典弹塑性理论中的流动法则。根据路径的变化,可以进一步分析强度应力和结构应变之间的变化规律,特别是在增量形式下,可以通过路径的切线方程,得到应力强度和结构应变之间的近似关系,这实质上就是增量形式的本构关系。对于某些特定的材料,如本文分析的理想弹塑性材料,可以得到与经典弹塑性理论完全形式上一致的结果。由此可以看到,全状态函数理论将经典弹塑性理论中的强度理论、流动法则和本构关系统一在了一个理论框架之下。
(3) 全状态函数的控制方程、状态路径方程和本构关系构成了理论的核心内容和方法
全状态函数理论在材料结构具有保持其状态不变趋势的假定上,建立了全状态函数的控制偏微分方程组,从而为材料结构全状态函数的求解奠定了基础。在此基础上,通过结构对外界响应假定其遵守最小能量原理,获得了材料结构在特定环境作用下的状态路径方程,为材料各参量的变化规律,建立了约束条件。在路径方程的基础上,通过采用路径切线方程的分析方法,可得到增量形式的本构关系。通过建立起的这样一个完整的分析步骤,使我们对结构性材料的分析,有了完整的分析方法。
通过对理想弹塑性材料的分析,在获得的平面形式、圆柱面形式和球面形式的特定解的特征,得到了与经典弹塑性理论中强度理论完全一致的结果。在路径分析中,得到了与经典弹塑性理论流动法则完全一致的结果。在路径切线方程的分析中,得到了与经典理论中的本构关系完全一致的结果。由此证实,全状态函数的控制方程、路径方程和本构关系构成的这一理论方法是完整的。另外,通过分析可以发现,与经典理论一致的这些结论和结果,分析中都给予了某些特定的约束条件,这告诉我们,约束条件的改变,将可能得到另外一些结果。也就是说,经典理论中的某些结论和结果,是某种情况下的特例。这从另一角度证实了,全状态函数理论具有的普遍意义。
(4) 形成了一条新的分析问题的思路
传统的经典理论的分析方法,大多以具体问题做为分析的出发点,往往局限于材料的某一种状态。全状态函数理论着眼于材料结构状态变化的整体集合,以考察材料结构变化所有的可能状态为出发点,了解和分析结构材料的变化规律和特征。通过建立起这样一种分析的新思路,跳出了过去分析材料特性的方法限制,从而为建立新的分析方法奠定了基础。在掌握了整体的材料结构状态变化规律的基础上,对于材料受到的某环境的特定作用,就可以理解为是结构状态变化的某种特例。具体讲,任何特定环境的作用,导致的材料结构的变化,必然受限于整体的材料结构变化规律。材料结构全状态函数理论建立起了这样一条新的分析思路:全状态函数-----状态路径方程-----本构关系。这实际上是一条从整体到局域,再到点的分析的过程。这一思路类似于数论中集合论,通过对数的大类分析,来掌握具体数的性质。
5. 结论
通过以上对理想结构的弹塑性材料的分析,对材料结构全状态函数理论有了一个总体、深入的了解,由此可以得到以下几点结论:
(1) 全状态函数理论作为一种解决材料结构性的方法,即解决复杂材料的理论体系,对于解决理想弹塑性材料这类简单材料,是完全有效可行的。可以得到几乎与经典弹塑性理论完全一致的结论和结果,但其实质性概念已完全不同。
(2) 证明了全状态函数理论在解决结构性材料问题上,已形成了一套完整的概念体系和方法,这主要体现为材料结构全状态函数的控制方程、状态路径方程和本构关系方程。这三项内容构成了全状态函数理论的核心内容和方法。
(3) 全状态函数理论以统一的概念和方法,将经典弹塑性理论中的强度理论、流动法则和本构关系统一了起来,并赋予了三项概念新的意义:复杂应力情况下的强度理论只是全状态函数在应力子空间中的体现,流动法则是特定环境作用下,材料在全状态函数面上的特定路径,本构关系是路径曲线上点的增量关系。
(4) 全状态函数理论提供了一种新的分析和考虑问题的思路:从整体到局部。
总之,材料结构的全状态函数理论作为解决材料结构性的一种方法,通过对理想弹塑性这类材料的分析,已初步体现出了他特有的可行性和优越性。对于更复杂材料或复杂情况的分析,还需要我们做进一步的工作,这里也希望有更多的有识之士加入到这一领域的研究中来。
文章引用
卫振海,王梦恕,张顶立. 弹塑性材料全状态函数特征研究
Research on Characteristics of All State Function of Elastic-Plastic Materials[J]. 力学研究, 2017, 06(02): 114-130. http://dx.doi.org/10.12677/IJM.2017.62013
参考文献 (References)
- 1. 朱合华, 张琦, 章连洋. Hoek-Brown强度准则研究进展与应用综述[J]. 岩石力学与工程学报, 2013, 10(36): 1945- 1963.
- 2. 牛杰, 刘光连, 田杰, 张雅鑫, 孟力平. 几个强度理论的屈服实验研究[J]. 工程力学, 2014, 1(31): 181-187.
- 3. 薛守义. 净剪应变比能强度理论研究[J]. 土木工程学报, 2012, 9(45): 122-127.
- 4. 邱士利, 冯夏庭, 张传庆, 黄书岭. 均质各向同性硬岩统一应变能强度准则的建立及验证[J]. 岩石力学与工程学报, 2013, 4(32): 715-727.
- 5. 张小波, 赵光明, 孟祥瑞. 考虑峰后应变软化与扩容的圆形巷道围岩弹塑性D-P准则解[J]. 采矿与安全工程学报, 2013, 6(30): 903-916.
- 6. 隋凤涛, 王士杰. 统一强度理论在地基承载力确定中的应用研究[J]. 岩土力学, 2011, 10(32): 3038-3042.
- 7. 刘德稳, 许纯梅, 邓勇亮, 郭春丽. 关于“土的剪切空间滑动面分析及各向异性强度准则研究”的讨论[J]. 岩土工程学报, 2013, 10(32): 1947-1949.
- 8. 尤明庆. 完整岩石的强度和强度准则[J]. 复旦学报(自然科学版), 2013, 5(52): 569-582.
- 9. 俞茂宏. 线性和非线性的统一强度理论[J]. 岩石力学与工程学报, 2007, 4(26): 662-669.
- 10. Gao, X.L. and Liu, M.Q. (2012) Strain Gradient Solution for the Eshelby-Type Polyhedral Inclusion Problem. Journal of the Mechanics and Physics of Solids, 60, 261-276. https://doi.org/10.1016/j.jmps.2011.10.010
- 11. Zhao, X.H. (2012) A Theory for Large Deformation and Damage of Interpenetrating Polymer Networks. Journal of the Mechanics and Physics of Solids, 60, 319-332. https://doi.org/10.1016/j.jmps.2011.10.005
- 12. 胡亚元. 基于Hill原理的非相关联流动法则的机理研究[J]. 浙江大学学报(工学版), 2013, 7(47): 1192-1198.
- 13. 杨强, 冷旷代, 张小寒, 刘耀儒. Drucker—Prager弹塑性本构关系积分:考虑非关联流动与各向同性硬化[J]. 工程力学, 2012, 8(29): 165-171.
- 14. 赵炼恒, 孙秋红, 黄阜, 邹金锋. 非关联流动准则对浅埋隧道稳定性影响的上限分析[J]. 公路交通科技, 2012, 12(29): 101-106.
- 15. 王红, 袁鸿, 夏晓舟, 章青. 基于最小耗能原理的塑性应变流动法则[J]. 上海大学学报(自然科学版), 2012, 4(18): 390-395.
- 16. 冷飞, 林皋. 塑性流动法则的相关性[J]. 哈尔滨工业大学学报, 2012, 4(18): 390-395.
- 17. 魏匡民, 苏佩珍. 有限元法中非关联流动条件下刚度矩阵的存储方式及平衡方程求解[J]. 三峡大学学报(自然科学版), 2011, 5(33): 11-14.
- 18. 孔位学, 芮勇勤, 董宝弟. 岩土材料在非关联流动法则下剪胀角选取探讨[J]. 岩土力学, 2009, 11(30): 3278-3282.
- 19. 王亚军, 张我华. 双重流动法则下地基黏塑性随机有限元方法[J]. 浙江大学学报(工学版), 2010, 4(44): 798-805.
- 20. 杨雪强, 陈晓平, 宫全美, 孙汉芳. 砂土的剪胀方程及其塑性势(I): 发展现状[J]. 广东工业大学学报, 2012, 1(29): 9-14.
- 21. 张然, 武建勋. 粒状体流动法则的微观机制[J]. 哈尔滨工业大学学报, 2009, 10(41): 247-250.
- 22. Ehre, A.E. and MikhailItskov, M.B. (2011) A Continuum Constitutive Model for the Active Behaviour of Skeletal Muscle. Journal of the Mechanics and Physics of Solids, 59, 625-636. https://doi.org/10.1016/j.jmps.2010.12.008
- 23. Gurses, E. and Sayed, T.E. (2011) A Variational Multiscale Constitutive Model for Nanocrystalline Materials. Journal of the Mechanics and Physics of Solids, 59, 732-749. https://doi.org/10.1016/j.jmps.2010.10.010
- 24. 牛斌, 杨海天. 基于均匀化方法的斜交节理岩体复合本构关系研究[J]. 岩土工程学报, 2007, 5(29): 773-778.
- 25. Berdichevsky, V.L. (2012) On the Origin of Microstructure Self-Similarity in Severe Plastic Deformation. Journal of the Mechanics and Physics of Solids, 60, 1-13. https://doi.org/10.1016/j.jmps.2011.10.006
- 26. 刘其鹏, 李锡夔, 楚锡华. 基于细观方向平均模型的颗粒材料宏观Cosserat连续体本构关系[J]. 计算力学学报, 2011, 5(28): 683-687.
- 27. 姚仰平, 牛雷, 崔文杰, 万征. 超固结非饱和土的本构关系[J]. 岩土工程学报, 2011, 6(33): 833-839.
- 28. Cui, W.J. and Wan, Z. (2011) UH Model for Unsaturated Soils. Chinese Journal of Geotechnical Engineering, 6, 833- 839.
- 29. 张志超, 程晓辉. 饱和土非等温固结和不排水剪切的热力学本构模型[J]. 岩土工程学报, 2013, 7(35): 1297-1306.
- 30. 相彪, 张宗亮, 迟世春, 林皋. 复杂应力路径下堆石料本构关系研究[J]. 岩土力学, 2010, 6(31): 1716-1728.
- 31. 卫振海, 王梦恕, 张顶立. 材料结构全状态函数本构关系模型研究[C]//全国结构工程学术会议. 第21届全国结构工程学术会议论文集: 2012年卷. 北京:《工程力学》杂志社, 2012: 10.
- 32. Wei, Z.H., Wang, M.S. and Zhang, D.L. (2013) A Research on the Full State Function Constitutive Relation Model. Springer, Berlin. https://doi.org/10.1007/978-3-642-32814-5_86
- 33. 卫振海. 岩土材料结构问题研究[D]: [博士学位论文]. 北京: 北京交通大学, 2012.
- 34. 卫振海, 王梦恕, 张顶立. 岩土材料结构分析[M]. 北京: 中国水利水电出版社, 2012.