Journal of Image and Signal Processing
Vol.
09
No.
02
(
2020
), Article ID:
34998
,
10
pages
10.12677/JISP.2020.92015
Research and Application of Seismic Image Enhancement Algorithm Based on Wavelet Transform
Wenjun Zhang, Chao Chen
Chengdu University of Information Technology, Chengdu Sichuan
Received: Mar. 21st, 2020; accepted: Apr. 6th, 2020; published: Apr. 13th, 2020

ABSTRACT
In recent years, with the rapid development of science and technology, as a mathematical analysis tool, wavelet transform with multi-scale resolution features has replaced the role of the traditional technical methods in many engineering applications. This thesis first introduces the basic theory of wavelet transformation and the basic principle of the related image in de-noising and enhancement. Second, the thesis is combined with the characteristics of the seismic image and the noise, and the seismic image de-noising and enhancement are discussed in detail by wavelet analysis. The soft and hard threshold methods have been selected. And the threshold function of the wavelet has been bettered; then the histogram equalization is used to improve the image contrast. Finally, it is concluded that the new threshold function can effectively remove the noise and obviously enhance the effect of the image de-noising.
Keywords:Seismic Image, Wavelet Transform, De-Noising and Enhancement, Histogram Equalization

基于小波变换的地震图像增强算法 研究与应用
张文军,陈超
成都信息工程大学,四川 成都
收稿日期:2020年3月21日;录用日期:2020年4月6日;发布日期:2020年4月13日

摘 要
近十几年来,随着科学技术的高速发展,小波变换作为一种数学分析工具,具有多尺度分辨特征,在许多工程应用领域已经取代传统的技术方法。本文首先介绍了关于小波变换的基本理论及相关图像去噪增强基本原理,结合地震图像及噪声特点,围绕小波分析法对地震图像去噪增强做了详细论述,采用了小波变换软、硬阈值方法,并对小波阈值函数进行相应的改进,再利用直方图均衡化提升图像对比度。经实验表明新阈值函数能够有效去除噪声,对地震图像去噪增强效果明显。
关键词 :地震图像,小波变换,去噪增强,直方图均衡化

Copyright © 2020 by author(s) and Hans Publishers Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY 4.0).
http://creativecommons.org/licenses/by/4.0/


1. 引言
我国石油、煤炭等地质资源丰富,也是最早发现并使用石油、天然气的国家,但人均占有量低,地质探明程度和认识程度也较低,其地质信息没有有效的利用,地震勘探是地质资源勘探开发工作中一种非常重要的方法 [1],但通常在地质资源勘探开发过程中由于采集地震数据仪器本身的缺陷或其他因素的作用,得到的地震信息图像数据是叠加在外界噪声因素上而被扭曲的,不能直接用来做某种地震解释或降低了地震解释的效率,需要对地震图像数据进行去噪增强处理,去除其中干扰成分,提高信噪比,从而更好地分析地质结构及地质资源分布,达到地质勘探目的。
图像增强是通过某些技术去提高图像的视觉效果,其图像增强方法有多种,从增强的作用域来看主要分为两大类:空间域增强和频率域增强 [2],小波变换是一种新的变换分析技术 [3],其局部变换方法式是基于空间和频率的,能从不同方向及尺度从图像信号中提取有用信息,通过伸缩和平移等运算功能可对其函数或原始信号进行多尺度的细化分析,采纳了短时傅里叶变换局部化的思想,同时又去除了其窗口大小不随频率等其他因素变化的缺点,被誉为“数学显微镜” [4] [5]。在语音合成、图像去噪增强、地震勘探等各方面得到广泛应用并取得巨大的成果。
小波理论的兴起,得益于其对信号的时域和频域的局部分析能力以及对一维有界函数的最优逼近性能,也得益于多分辨率分析概念的提出。1910年,Haar第一个提出正交小波基,其原理是由一个简单的二值函数作为母小波经平移和伸缩形成的,具有最优的时域分辨率,但频域分辨率特差,后续Coifman等相应提出一系列小波基,例如symN、dbN、coifN等。1984年,Morlet在分析地震波数据的局部性质时,发现用傅立叶变换难以达到要求,因此引入小波的概念应用于信号分析中,并用一种无限支集的非正交小波分析地震数据,小波分析取得突破进展,这是第一次真正意义上提出了小波的概念。1987年,Meyer和Mallat将计算机视觉领域中的多尺度分析思想引入到小波分析中,提出了多分辨率分析的概念,统一了在此前的所有具体正交小波的构造方法,同时给出了将信号和图像分解为不同频率通道的分解和重构快速算法,即Mallat算法。Mallat算法在小波分析发展中具有里程碑的意义,标志着第一代小波的开始,也是小波分析从纯理论走向实际运用。之后Donoho等在基于小波分析图像去噪增强方面做了大量研究,提出基于阈值处理思想的小波去噪技术,对小波系数进行阈值处理,保留有效的小波系数,再重构小波系数尽可能恢复原图像,近几年来,小波理论被广泛运用到地震图像数据处理之中,与传统的图像处理相比,取得的效果更佳,小波变换将成为地震图像数据去噪增强处理的一大主流技术。
2. 小波变换
2.1. 小波变换理论
设 为一平方可积函数,即 ,其傅里叶变换 [6],当满足如下容许条件
(1.1)
时, 为母小波,说明母小波在相应的频域内具有良好的衰减性。再将母函数 经过平移和伸缩后得到一个相应的小波序列,如下所示:
(1.2)
其中,a为伸缩因子,b为平移因子。
对于任意的函数 的连续变换小波为:
(1.3)
当小波为正交小波时,其对应的重构公式为:
(1.4)
为了满足完全重构条件以及在数值上是稳定的, 满足以下条件:
(1.5)
(1.6)
其中A、B的大小范围 。
2.2. 多分辨率分析理论
多分辨率分析其本质是把信号在一系列不同的尺度空间进行分解。随着尺度由大到小的变换,可以由粗到细地观察信号,类似于一台照相机的镜头由远及近地接近观察目标 [7] [8]。
在不同尺度下,对图像进行分解,本质是图像通过小波函数和尺度函数构造出来的滤波器进行操作处理,首先对原始图像的频谱进行第一层分解,分解为高频段H1和低频段L1,以此类推,对图像进行分解处理,分解层数越高,时间分辨率越低,但频率分辨率就越高。多尺度分解示意图如图1所示。
则恢复原信号,与分解操作相反。小波系数多尺度重构示意图如图2所示。
3. 图像增强
3.1. 基于小波变换的地震图像增强
小波阈值地震图像去噪增强的一大主流技术 [9],根据对含噪地震图像数据的分解,噪声信号的小波系数相对更小,地震图像中有用信号的小波系数相对更大,采用适合的阈值加以分离出来,对大部分噪声的小波系数置零处理,对用用信号的小波系数进行压缩或者保留不变 [10]。其基本操作步骤如下:
1) 分解:根据地震图像数据特点,对地震图像数据进行分解得到相应的小波系数。
2) 阈值处理:根据噪声和有用信号的小波系数的大小,选取适当的阈值进行处理,对噪声的小波系数进行去除,对有用信号的小波系数进行保留或者适当压缩处理。
3) 重构:处理后的小波系数需要通过重构得到去噪增强后的地震图像数据。

Figure 1. Decomposition diagram
图1. 分解示意图

Figure 2. Refactoring diagram
图2. 重构示意图
在对含噪地震图像数据处理时,阈值函数根据每层分解后的小波系数大小设置一个阈值,阈值函数的选取不恰当,则相应的阈值也会过大或者过小,处理的地震图像效果不佳 [11],以下为常用的两种阈值函数 [12] [13]。
1) 硬阈值函数:首先设置一个适当的阈值,对于大于阈值的小波系数进行保留不变,对于小于阈值的小波系数进行置零处理。其公式如下:
(2.1)
硬阈值函数图像如图3所示:
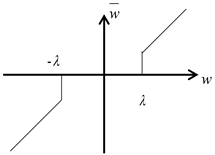
Figure 3. Hard threshold function
图3. 硬阈值函数
2) 软阈值函数:与硬阈值函数相比而言,软阈值函数只是大于阈值的小波系数进行了压缩处理,同样对于小于阈值的小波系数都置零处理。其公式如下:
(2.2)
软阈值函数图像如图4所示:
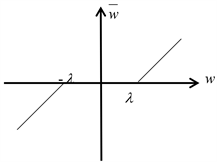
Figure 4. Soft threshold function
图4. 软阈值函数
3.2. 改进阈值函数算法
3.2.1. 一维循环
地震图像是二维图像,可先对其中一维波形进行阈值去噪增强,通过计算图像整体数据大小,得出整幅图像所占时间多少,以时间维度通过循环来逐步对地震图像数据整体来去噪增强。
3.2.2. 分层阈值算法
小波阈值分为全局阈值和分层阈值 [14],全局阈值所对应的全局阈值函数虽然能够有效地抑制随机噪声,但该阈值函数算法不能随地震图像数据每层分解后的小波系数变化而相应灵活变化,并没有取得最佳阈值,根据地震图像中的有用信号随着小波分解层数增加其小波系数而增大,其中噪声部分相反变化,分层阈值函数就能更好的对地震图像数据进行去噪增强,局部信息得到较好保留,滤波效果更佳 [15]。
(2.3)
(2.4)
其中N为图像数据大小, 为噪声方差,Median为小波变换第一层变换系数求得绝对值后,求出其中的中值结果。根据有用信号与噪声信号随分解层数增加小波系数表现出相反的特性以及小波系数相互之间的关系,得到本文的改进阈值公式为:
(2.5)
(2.6)
其中j代表小波的分解层数, 为第j层分解所对应的阈值。从公式中可以看出当 时,阈值函数可化为 ,与通用阈值函数sqtwolog相等,当 时,由导函数(2.6)可知分解层数j不断增加而阈值 不断减小,这也符合噪声的小波系数幅值随分解层数的增加而不断减小的特点,对每层阈值的设置更加合理,去噪增强效果明显改善。
3.3. 仿真分析
更好验证本文阈值函数的有效性,对含有随机噪声的地震图像数据进行分析,并选择全局软阈值、全局硬阈值、一维循环以及本文改进阈值算法对含噪地震图像数据进行去噪增强处理,图5、图6所示。

Figure 5. Original image and global threshold
图5. 原始图像及全局阈值

Figure 6. Original image and improved algorithm
图6. 原始图像及改进算法
便于更仔细观察去噪增强效果,从地震图像数据中截取一维地震道信号,如图7、图8所示。
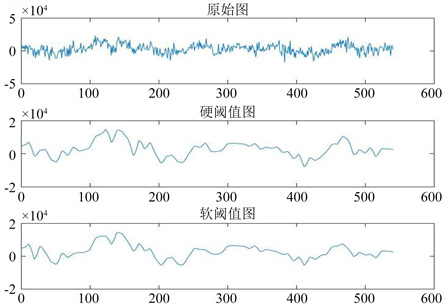
Figure 7. Global threshold denoising one-dimensional seismic trace signal
图7. 全局阈值去噪一维地震道信号
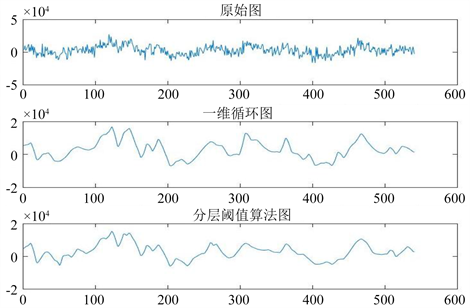
Figure 8. Improved threshold to denoise one-dimensional seismic trace signals
图8. 改进阈值去噪一维地震道信号
含有不同强度随机噪声的地震图像数据经过上述四种小波阈值去噪算法后所处理得到的SNR,如表1所示。
Table 1. Enhancement of wavelet threshold denoising at different intensities (SNR unit db)
表1. 不同强度下小波阈值去噪增强(SNR单位db)
从图5、图6、图7、图8中可看出,在小波阈值去噪增强中,全局硬阈值在细节部分保留完整,但在边缘突出变化部分,容易出现伪吉布斯效应;在全局软阈值中,滤波效果好,图像质量提升,但细节部分容易出现模糊现象;在一维循环中,对图像细节部分处理更加精细,但是容易出现伪吉布斯效应 [16],运算效率低,适用于小型图像数据;在改进分层阈值算法中,相比之下,地震图像的细节部分和轮廓区域处理效果更佳,更接近于原始图像,视觉效果好。综合来看,改进的分层阈值算法的信噪比比其他去噪增强方法更高,噪声滤波处理效果更好。
4. 直方图均衡化
直方图均衡化的处理方法是首先对图像各灰度级概率进行积累 [17],并作为分布函数,在一定灰度范围内,再将原图映射为灰度级均匀分布的图像。针对于 大小的图像,其直方图均衡化表达式为 [18]:
(3.1)
(3.2)
其中 每一像素值所占灰度级概率, 为累积分布函数。
仿真分析
地震图像经过小波阈值图像去噪后,再次通过直方图均衡化对其地震图像进行操作,细节等有用信息突出明显,如图9、图10所示。
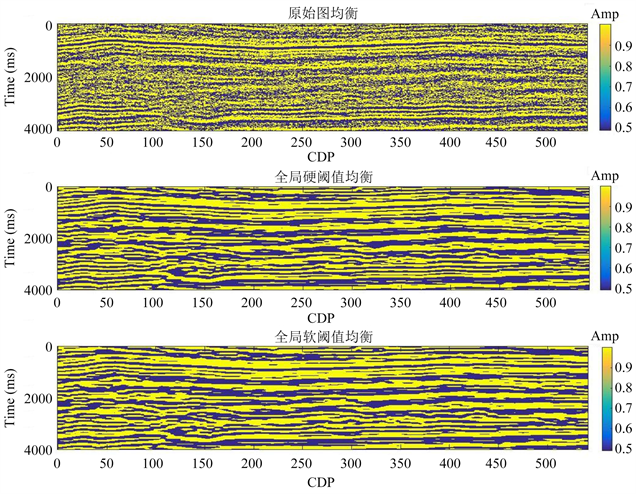
Figure 9. Global threshold histogram equalization
图9. 全局阈值直方图均衡化
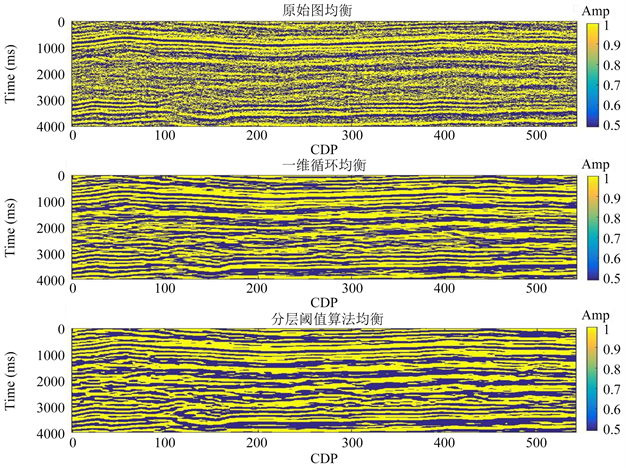
Figure 10. Improved threshold histogram equalization
图10. 改进阈值直方图均衡化
对地震图像直方图均衡化操作处理后,对比度明显提升,可清晰看出去噪效果异同,便于地质勘探等方面研究。
5. 总结和展望
地震图像是地质勘探等方面获取有效信息的途径之一,其图像质量的提高改善非常关键,近年来,小波变换技术用于地震图像去噪增强得到广泛关注,本文主要对小波变换算法进行MATLAB仿真实验分析,根据地震图像有用信号与噪声分解后的特点,对分层阈值函数进行改进,对去噪后图像再通过直方图均衡化提升细节视觉信息变化,地震图像细节、轮廓等信息得到有效保留,地震图像增强视觉效果更加明显。
目前,地震图像去噪增强技术并没有完全解决实际中的问题,在未来基于小波变换地震图像增强方法还得更深入研究。
1) 实际生活中,噪声的不同,其去噪增强效果也不一样,需要在不同噪声及强度情况下,深入对小波变换的阈值和阈值函数进行改善。
2) 本文仅是对小波阈值地震图像去噪增强进行了优化,既要完全去除含噪地震图像中的噪声,又要更加完整保留地震图像中的有用信息,是非常困难的,许多问题还没得到很好解决,所以在这方面还需要更深层次的钻研。
文章引用
张文军,陈 超. 基于小波变换的地震图像增强算法研究与应用
Research and Application of Seismic Image Enhancement Algorithm Based on Wavelet Transform[J]. 图像与信号处理, 2020, 09(02): 119-128. https://doi.org/10.12677/JISP.2020.92015
参考文献
- 1. 丁西明. 基于小波变换的图像增强研究[D]: [硕士学位论文]. 合肥: 安徽大学, 2010.
- 2. 唐世伟. 地震解释中的图像处理方法与技术研究[D]: [博士学位论文]. 大庆: 东北石油大学, 2011.
- 3. 赵玉宝. 小波变换在地震信号去噪中的应用研究[D]: [硕士学位论文]. 长沙: 中南大学, 2005.
- 4. 王惠, 王宇, 蔡光程. 基于小波阈值的图像增强算法[J]. 电脑知识与技术(学术交流), 2007, 4(23): 1405-1408.
- 5. 姚胜利. 地震信号的小波去噪方法研究[D]: [硕士学位论文]. 长沙: 中南大学, 2007.
- 6. 何瑞强. 基于小波变换的图像去噪方法[D]: [硕士学位论文]. 西安: 西安建筑科技大学, 2009.
- 7. 祖国峰. 基于小波变换的地震图像增强方法研究与应用[D]: [硕士学位论文]. 大庆: 东北石油大学, 2011.
- 8. 王伟. 基于小波变换的图像去噪方法研究[D]: [硕士学位论文]. 广州: 华南理工大学, 2012.
- 9. 张晓辉. 基于自适应阈值的图像增强算法[D]: [硕士学位论文]. 北京: 北方工业大学, 2015.
- 10. 安雪娇. 基于小波变换的图像去噪和增强研究[D]: [硕士学位论文]. 兰州: 西北师范大学, 2015.
- 11. Hsung, T.-C., Lun, D.P.-K. and Ng, W.W.L. (2011) Efficient Fringe Image Enhancement Based on Dual-Tree Complex Wavelet Transform. Applied Optics, 50, 3973-3986.
https://doi.org/10.1364/AO.50.003973 - 12. 高文仲. 小波分析在图像去噪中的应用研究[D]: [硕士学位论文]. 上海: 华东师范大学, 2013.
- 13. 黄敏敏. 基于小波分析的图像去噪、图像融合的应用研究[D]: [硕士学位论文]. 成都: 电子科技大学, 2009.
- 14. 张郝. 基于小波变换的图像去噪方法研究[D]: [硕士学位论文]. 北京: 北京交通大学, 2008.
- 15. 付燕. 人工地震信号去噪方法研究[D]: [博士学位论文]. 西安: 西北工业大学, 2002.
- 16. Rallabandi, V.P.S. (2008) Enhancement of Ultrasound Images Using Stochastic Resonance-Based Wavelet Transform. Computerized Medical Imaging and Graphics, 32, 316-320.
https://doi.org/10.1016/j.compmedimag.2008.02.001 - 17. 郑辉, 吴谨. 基于小波分频与直方图均衡的图像增强算法[J]. 现代电子技术, 2010, 33(16): 149-150+153.
- 18. 张国伟. 基于小波变换的图像去噪方法研究[D]: [硕士学位论文]. 昆明: 昆明理工大学, 2014.
