Dynamical Systems and Control
Vol.06 No.04(2017), Article ID:22539,7
pages
10.12677/DSC.2017.64023
Study on Firing Patterns for a Four-Dimensional Neuron Model
*通讯作者。
Huoxia Liu, Xuanliang Liu*
School of Mathematics, South China University of Technology, Guangzhou Guangdong

Received: Oct. 1st, 2017; accepted: Oct. 19th, 2017; published: Oct. 31st, 2017

ABSTRACT
This paper studies a sciatic nerve chronic constriction injury model. This model consists of four coupled nonlinear differential equations. By using the fast-slow dynamical methods and numerical simulations, we analyze the firing patterns of the model. We give the single parameter bifurcation diagrams of the fast subsystem, and discuss the stable limit cycles which are corresponding to the firing state of the neuron. Dynamical mechanisms of different firing patterns are obtained.
Keywords:Four-Dimensional Neuron Model, Fast-Slow Dynamics, Bifurcation, Bursting
一类四维神经元模型的放电模式研究
刘火霞,刘宣亮*
华南理工大学数学学院,广东 广州
Email: *liuliang@scut.edu.cn
收稿日期:2017年10月1日;录用日期:2017年10月19日;发布日期:2017年10月31日

摘 要
本文研究一类描述坐骨神经慢性压迫性损伤的四维神经元模型。利用快慢动力学方法,并结合数值模拟结果来分析此模型的各种放电模式。通过作出快子系统随慢变量变化的单参数分岔图,以及对相应于放电状态的稳定极限环的讨论,来得到不同放电模式出现的动力学机制。
关键词 :四维神经元模型,快慢动力学,分岔,簇放电

Copyright © 2017 by authors and Hans Publishers Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/


1. 引言
对应不同的放电模式,神经元有着不同的编码和信息处理方式。利用动力系统的分岔理论和快慢动 力学方法来研究神经元模型的不同类型的放电模式,是近几十年被大量采用和行之有效的方法,可参见文献 [1] - [6] 等。如最早由Rinzel [1] 在研究神经元簇放电模式时提出的“切片法”(dissection),将神经元模型看成快慢动力系统来研究,即将模型中的变量分为快变量和慢变量,快变量负责动作电位的产生,而慢变量起着调节快变量的作用,其动力学行为表现为静息状态与反复放电状态的相互转迁,从而产生出簇放电。
为了与试验数据相吻合,文 [7] 将描述坐骨神经慢性压迫性损伤的三维Chay模型 [8] [9] 进行了改进,变为如下四维神经元模型
(1)
其中V为膜电压,n为钾离子通道激活的概率, 为细胞内钙离子浓度, 对应内质网上腔钙浓度。参数 分别表示混合Na+-Ca2+通道,电压依赖K+通道(或钙依赖K+通道),泄漏离子通道和Ca2+通道的反转电位, 分别代表各通道的最大电导除以膜电容, 分别为混合Na+-Ca2+ 通道激活和失活的概率, 为n的稳定态值, 是松弛时间, 表示细胞内钙离子流出的比例常数, 表示钙库中Ca2+-ATPase的泵激活率, 和 分别表示 的释放率和 的离解常数。用y表示h、
m或n,则由 可得 和 ,其中 的表达式如下
, , , ,
, , .
在本文中,参数值取为
, , , , ,
, , , , , , , .
在文 [7] 中,作者通过数值模拟,对模型(1)进行了分析,讨论了加周期分岔、混沌在峰放电和簇放电中的变化过程等复杂动力学现象,说明了四维模型(1)与三维Chay模型相比,其放电模式与实验数据更加吻合。在本文中,我们将利用分岔和快慢动力学方法 [1] [10] ,结合分岔软件MATCONT的使用,对产生模型(1)的几种放电模式的动力学机制进行研究。
2. 分岔和快慢动力学分析
由于变量 改变的速率远慢于其他的变量 ,因此我们将 作为快变量,将 作为慢变量,即将模型(1)看成由快子系统
(2)
和慢子系统
(3)
构成,将慢变量 作为快变子系统(2)的分岔参数。
令模型(1)的四个方程的右端为零,得到平衡点满足的方程组。现取模型(1)的后两个方程的右端为零,然后相加,得到 ,由此解出 ,代入(3)的右端为零的式子,可求得
。 (4)
于是,由(2)的三个方程右端为零和(4)式构成的方程组的解即为(1)的平衡点坐标。因此由系统(2)在 平面作出的随分岔参数 变化的平衡点曲线与方程(4)确定的曲线的交点即为(1)的平衡点。
下面通过选取几个不同的 值,利用快慢动力学方法来分析模型(1)的不同的放电模式的动力学机制。本文使用的方法,与文 [11] 中研究三维Chay模型的不同的簇放电模式的方法类似。我们分以下5种情形来讨论。
2.1. vk = −70
图1(a)为vk = −70时神经元模型(1)的膜电位V的时间历程图,其放电模式为簇放电模式。为了分析产生此放电模式的动力学机制,我们作出了含有单参数分岔的几何分析图(图1(b))。
在图1(b)中,黑色实线和虚线构成的Z型曲线为快子系统(2)的平衡点曲线,上支和下支的实线部分对应稳定平衡点曲线,中支的虚线部分对应不稳定平衡点曲线,点画线为方程(4)表示的曲线。 与 点分别为系统(2)的鞍结分岔点,P点为点画线与平衡点曲线的不稳定部分的交点,对应模型(1)的不稳定平衡点(图1(b)中小空心圆点)。图中附加的蓝色曲线为模型(1)的轨线在 平面的投影曲线,与上支和下支的稳定平衡点曲线有部分重合。
当分岔参数 减少时,位于Z型平衡点曲线下支附近出发的(1)的轨线,沿着下支到达鞍结分岔点
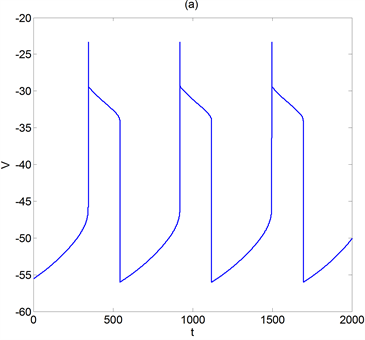
Figure 1. vk = −70. (a) Time course of membrane potential; (b) geometric analysis diagram
图1. vk = −70。(a) 膜电位的时间历程图;(b) 几何分析图
,然后向上转迁到Z型平衡点曲线上支的稳定平衡点附近,此时分岔参数 增加,(1)的轨线沿着上支到达鞍结分岔点 ,然后又转迁到Z型平衡点曲线的下支,随着 减少又重复上述过程,从而产生出图1(a)的簇放电模式。按照文 [3] 的分类,此簇放电模式为“fold/fold”点-点滞后环型簇放电。
以下文中出现的图中各曲线、点的意义与图1中相同,不再重复。
2.2. vk = −76
图2(a)为vk = −76时神经元模型(1)的膜电位v的时间历程图,图2(b)为相应的几何分析图。在图2(b)中,Z型平衡点曲线的下支和中支仍然分别为(2)的稳定平衡点曲线和不稳定平衡点曲线,上支中 和 皆为超临界的Hopf分岔点(靠近 右方还有一个次临界的Hopf分岔点未标出),在 左边和 到 部分对应稳定平衡点曲线, 到 部分对应不稳定平衡点曲线。红色曲线 分别表示快子系统(2)随参数 变化时所产生的一族稳定极限环上的膜电位 的最大值和最小值曲线(在后面的几何分析图中 表示意义一样)。点画线与平衡点曲线的不稳定部分的交点P,对应模型(1)的不稳定平衡点。
当分岔参数 减少时,位于Z型平衡点曲线下支附近出发的(1)的轨线,沿着下支到达鞍结分岔点 ,然后向上转迁到Z型平衡点曲线上支的稳定平衡点附近,此时分岔参数 增加,(1)的轨线沿着上支到达 ,然后环绕 曲线向右延伸到 , 经过 后沿着平衡点曲线附近到达 点,然后转迁到Z型平衡点曲线的下支,随着 减少又重复上述过程,从而产生出图2(a)的簇放电模式。按照文 [3] 的分类,此簇放电模式为经由“fold/fold”滞后环的“Hopf/Hopf”型簇放电。
2.3. vk = −80
图3(a)为vk = −80时神经元模型(1)的膜电位v的时间历程图,图3(b)为相应的几何分析图。在图3(b)中,z型平衡点曲线的下支和中支分别为(2)的稳定平衡点曲线和不稳定平衡点曲线,上支中 和 皆为超临界的Hopf分岔点(靠近 右方还有一个次临界的Hopf分岔点未标出),在 左边和 到 部分对应稳定平衡点曲线, 到 部分对应不稳定平衡点曲线。点画线与平衡点曲线的不稳定部分的交点P,对应模型(1)的不稳定平衡点。
当分岔参数 减少时,位于z型平衡点曲线下支附近出发的(1)的轨线,沿着下支到达鞍结分岔点
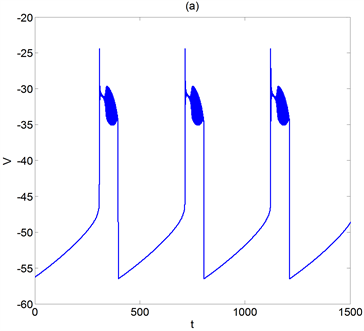
Figure 2. vk = −76. (a) Time course of membrane potential; (b) geometric analysis diagram
图2. vk = −76。(a) 膜电位的时间历程图;(b) 几何分析图

Figure 3. vk = −80. (a) Time course of membrane potential; (b) geometric analysis diagram
图3. vk = −80。(a) 膜电位的时间历程图;(b) 几何分析图
,然后向上转迁到z型平衡点曲线上支并环绕 曲线向右延伸到 , 经过 后沿着平衡点曲线附近到达 点,然后转迁到z型平衡点曲线的下支,随着 减少又重复上述过程,从而产生出图3(a)的簇放电模式。由文 [3] 知,此簇放电模式为经由“fold/fold”滞后环的“fold/Hopf”型簇放电。
2.4. vk = −87
图4(a)为vk = −87时神经元模型(1)的膜电位V的时间历程图,图4(b)为相应的几何分析图。在图4(b)中,z型平衡点曲线的下支和中支分别为(2)的稳定平衡点曲线和不稳定平衡点曲线,上支中H为超临界的Hopf分岔点(靠近H点右方还有一个次临界的Hopf分岔点未标出),在H左边部分对应不稳定平衡点曲线,H到 部分对应稳定平衡点曲线。点画线与平衡点曲线的不稳定部分的交点P,对应模型(1)的不稳定平衡点。
此时根据几何分析图图4(b)进行的快慢动力学分析与vk = −80时的分析完全一致,得到的簇放电模式也为经由“fold/fold”滞后环的“fold/Hopf”型簇放电。
2.5. vk = −103
图5(a)为vk = −103时神经元模型(1)的膜电位V的时间历程图,图5(b)为相应的几何分析图。在图5(b)中,z型平衡点曲线的下支和中支分别为(2)的稳定平衡点曲线和不稳定平衡点曲线,上支中H点为超临界的Hopf分岔点(靠近H右方还有一个次临界的Hopf分岔点未标出),且在H点左边部分对应不稳定平衡点曲线,在H到 部分对应稳定平衡点曲线。点画线与平衡点曲线的稳定部分的交点P,对应模型(1)的稳定平衡点(在图5(b)中为实心圆点)。

Figure 4. vk = −87. (a) Time course of membrane potential; (b) geometric analysis diagram
图4. vk = −87。(a) 膜电位的时间历程图;(b) 几何分析图

Figure 5. vk = −103. (a) Time course of membrane potential; (b) geometric analysis diagram
图5. vk = −103。(a) 膜电位的时间历程图;(b) 几何分析图
我们选取模型(1)的初始点坐标 ,随着分岔参数 的增加,(1)的轨线环绕 曲线向右延伸到H,经过H后沿着平衡点曲线到达 点,然后转迁到Z型平衡点曲线的下支,随着 减少最后趋向于稳定平衡点P,神经元最终到达静息状态。在文 [4] 中称此放电状态为簇兴奋模式。
3. 结论
文 [7] 建立了一类坐骨神经慢性压迫性损伤的四维神经元模型,并通过参数的变化,讨论了该模型复杂的放电模式。本文对此四维神经元模型,利用分岔和快慢动力学的方法,选取与文 [7] 不同的参数变化,即通过 的不同取值,来讨论模型的几种放电模式,即“fold/fold”点-点滞后环型簇放电,经由“fold/fold”滞后环的“Hopf/Hopf”型簇放电和“fold/Hopf”型簇放电,以及簇兴奋模式,得到了产生相应的放电模式的快慢动力学机制。通过对产生神经元不同的放电模式的动力学研究,使我们对神经元及神经网络的信息处理方式有更深入的理解。
基金项目
国家自然科学基金(11572127)。
文章引用
刘火霞,刘宣亮. 一类四维神经元模型的放电模式研究
Study on Firing Patterns for a Four-Dimensional Neuron Model[J]. 动力系统与控制, 2017, 06(04): 180-186. http://dx.doi.org/10.12677/DSC.2017.64023
参考文献 (References)
- 1. Rinzel, J. (1985) Bursting Oscillations in an Excitable Membrane Model. Lecture Notes in Mathematics, 1151, 304-316. https://doi.org/10.1007/BFb0074739
- 2. Rinzel, J. and Ermentrout, B. (1998) Analysis of Neural Excitability and Oscillations. In: Koch, C. and Segev, I., Eds., Computational Neuroscience, MIT Press, Cambridge, 135-169.
- 3. Izhikevich, E.M. (2000) Neural Excitability, Spiking and Bursting. International Journal of Bifurcation and Chaos, 10, 1171-1266. https://doi.org/10.1142/S0218127400000840
- 4. Izhikevich, E.M. (2007) Dynamical Systems in Neuroscience. The Geometry of Excitability and Bursting. MIT Press, Cambridge.
- 5. Shilnikov, A.L. and Cymbalyuk, G. (2005) Transition between Tonic Spiking and Bursting in a Neuron Model via the Blue-Sky Catastrophe. Physical Review Letters, 94, 048101. https://doi.org/10.1103/PhysRevLett.94.048101
- 6. Shilnikov, A.L. (2012) Complete DYNAMICAL Analysis of a Neuron Model. Nonlinear Dynamics, 68, 305-328. https://doi.org/10.1007/s11071-011-0046-y
- 7. Gu, H.G. and Pan B.B. (2015) A Four-Dimensional Neuronal Model to Describe the Complex Nonlinear Dynamics Observed in the Firing Patterns of a Sciatic Nerve Chronic Con-striction Injury Model. Nonlinear Dynamics, 81, 2107-2126. https://doi.org/10.1007/s11071-015-2129-7
- 8. Chay, T R. (1985) Chaos in a Three-Variable Model of an Ex-citable Cell. Physica D, 16, 233-242. https://doi.org/10.1016/0167-2789(85)90060-0
- 9. Chay, T.R., Fan, Y.S. and Lee, S. (1995) Bursting, Spiking, Chaos, Fractals and Universality in Biological Rhythms. International Journal of Bifurcation and Chaos, 5, 595-635. https://doi.org/10.1142/S0218127495000491
- 10. Kuznetsov, Y.A. (1998) Elements of Applied Bifurcation The-ory. 2nd Edition, Spring-Verlag, New York.
- 11. 杨卓琴, 陆启韶. 神经元Chay模型中不同类型的簇放电模式[J]. 中国科学G辑, 2007, 37(4): 440-450.